Тема 2: Основные тригонометрические тождества Проверочный тест:

1. Найдите:

   1. sinx и tgx, если сosx =1/5, x [- π/2;0].

   2. cosx, если tgx=2, x [ π; 3π/2].

2. а) Найдите sin(α+β), если sinα =3/5, а cosβ=⅓ , α [π/2; π], β [0; π/2],

б) Упростите: .

3. а) Найдите: сos 210°; sin(-135°); tg (11π/6).

б) Упростите: .

4. а) Найдите sin2α; cos2α; tg2α, если tgα=5, α [0; π/2]

б) Найдите sinx, cosx, tgx, если cos2x= , x [π/2; π].

5. Упростите:

Ответы:

1. а) - ; б) ; 2.а) ; б) 1; 3. а) - ; - ; - ; б) ; 4. а) - ; - ; б) ; - ; - ; 5. - .

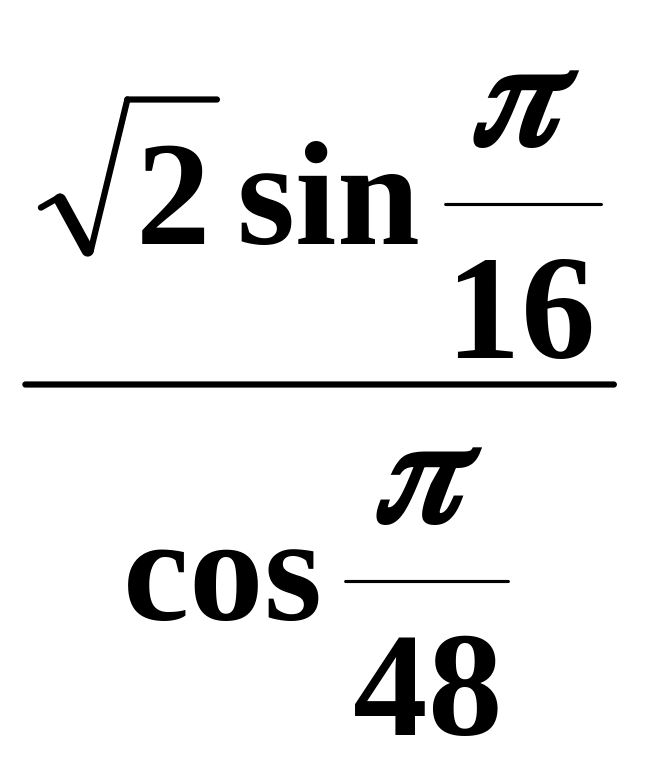Улучшите свои знания

1.Тригонометрические функции одного и того же аргумента

1. sin²x + cos²x =1

- сумма квадратов синуса и косинуса одного и того же аргумента равна 1.

По этой формуле, зная значения синуса какого – нибудь угла (например, sinx =1/3), можно найти косинус этого же угла (cos²x =1- sin²x =1-(1/3)²=

=1-1/9=8/9, cosx=±2 . Знак cosx зависит от того, в какой четверти

находится угол х.

Зная значения косинуса какого – нибудь угла, по этой формуле можно

найти синус этого же угла: найдем sinx, если сosx=1/5, x [- π/2;0];

sin²x=1-cos²х =24/25, sinx=-2 , так как при x [- π/2;0] sinx<0.

2. 

где x ≠ π/2+ πn, n – любое целое число; где x ≠ πn, n – любое целое число

3. ctg²x +1 = 1/ sin²x, x≠ πn, n – любое целое число.

По этой формуле, зная значения котангенса какого - нибудь угла (например, ctgx =4), можно найти синус этого же угла, т.е. sinx.

(sinx= = , знак зависит от того, в какой четверти находится угол х)

4. tg²x +1 = 1/ cos²x, x≠π/2+ πn, n – любое целое число.

По этой формуле, зная значения тангенса какого – нибудь угла (например,

tgx =5, x [π/2; π] ), можно найти косинус этого же угла, т.е. cosx.

(cosx = - = , знак «- », так как при x [π/2; π] cosx<0)

5. tgx∙ctgx=1, x≠ , n – любое целое число.

Пример:

Найдите значения всех тригонометрических функции угла x, если

tgx =0.75, x [π; 3/2π]

Решение

Из формулы tgx∙ctgx=1 найдем ctgx=1/tgx =1:0.75 = 4/3.

Из формулы tg²x +1 = 1/ cos²x найдем cosx = - , знак «- » , берется потому, что при x [π; 3/2π] cosx<0.

Из формулы найдем sinx = cosx∙tgx =- 0.8∙0.75 = -0.6.

2.Формулы сложения тригонометрических функций

1. Синус суммы двух углов:

sin(x +y) =sinxcosy + sinycosx

2. Синус разности двух углов:

sin(x -y) =sinxcosy - sinycosx

3. Косинус суммы двух углов:

cos(x+y) = cosxcosy – sinx siny

4. Косинус разности двух углов:

cos(x-y) = cosxcosy + sinx siny

5. Тангенс суммы двух углов:

tg(x+y) = , где

x+y≠ π/2+ πn, x≠π/2+πk, y≠π /2+πm, n,m,k – целые числа.

6. Тангенс разности двух углов:

tg(x-y) = , где

x- y≠ π/2+ πn, x≠π/2+πk, y≠π /2+πm, n,m,k –целые числа.

Примеры:

а) Найдите cos(x+y), если sinx =3/5, а cosy=⅓ , x [π/2; π], y [0; π/2].

Решение

Запишем формулу cos(x+y) = cosx cosy – sinx siny. В правой части этой формулы значения cosx и siny не известны .Найдем их:

cosx = - = , siny = = .

Подставим найденные значения в формулу cos(x+y) = cosxcosy – sinx siny, получим: cos(x+y)= .

б) Упростите выражение: .

Решение

Замечаем, что в числителе представленной дроби записана правая часть формулы косинуса разности двух углов, т.е.

cos 110°cos40° +sin 110° sin 40° = cos(110° – 40°)= cos70°.

В знаменателе представленной дроби записана правая часть формулы синуса разности двух углов, т.е.

sin 35°cos15° – cos35°sin15°=sin(35° – 15°) = sin 20°. Тогда получим:

= , cos 70° = sin20°,т.к. 20° дополняет 70° до 90°.