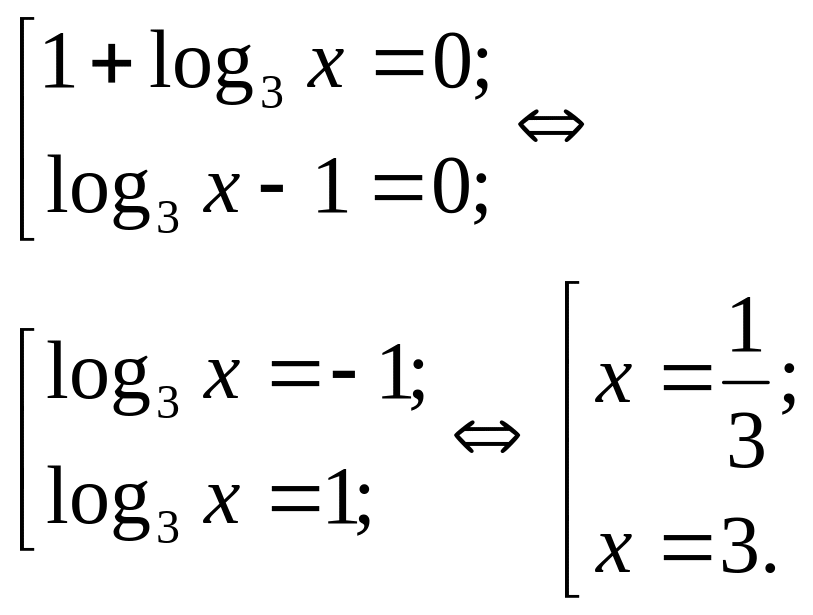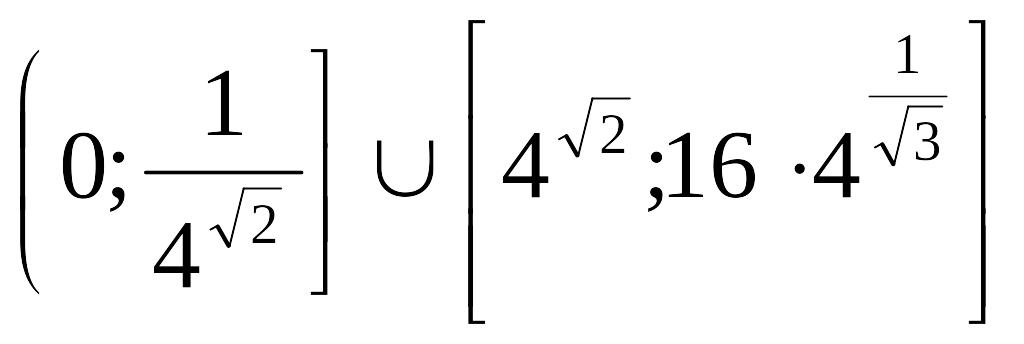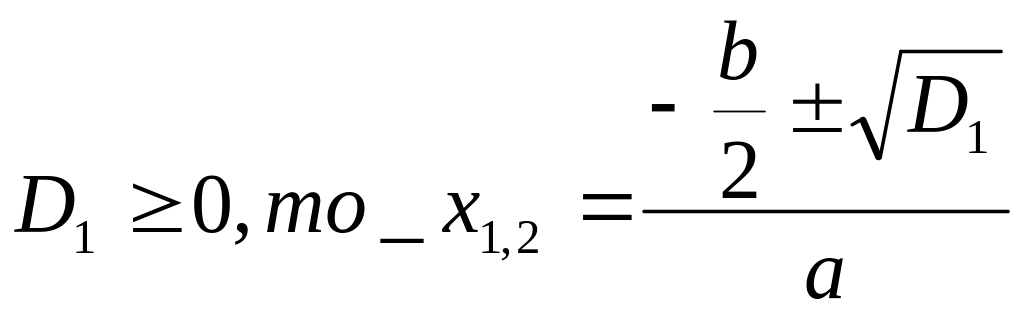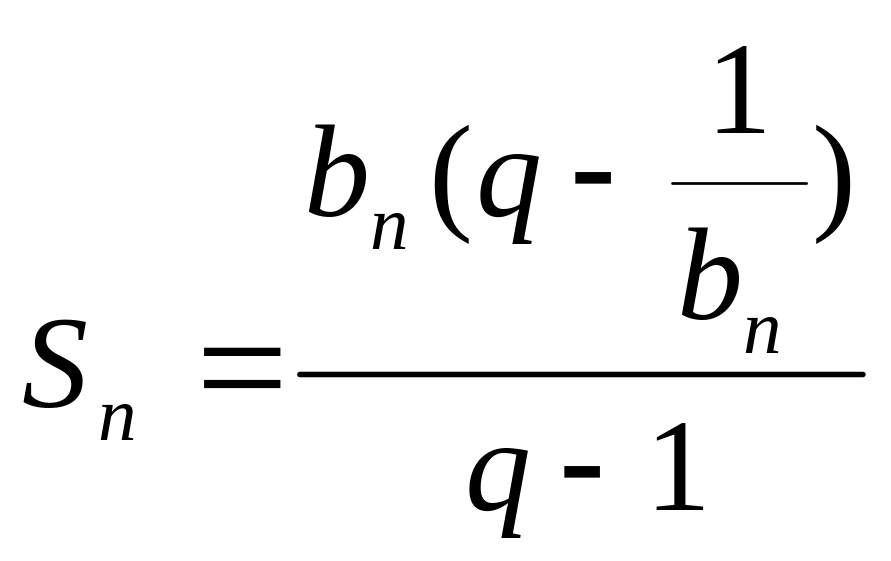- •Алгебра и начала анализа Тема 1 Тригонометрические функции Проверочный тест
- •Ответы:
- •Улучшите свои знания
- •Наиболее часто встречающиеся ошибки
- •Контрольный тест
- •Найдите:
- •Тема 2: Основные тригонометрические тождества Проверочный тест:
- •Найдите:
- •Ответы:
- •Улучшите свои знания
- •1.Тригонометрические функции одного и того же аргумента
- •2.Формулы сложения тригонометрических функций
- •Формулы приведения
- •4.A) Формулы двойного аргумента
- •Тангенс двойного аргумента:
- •1.Синус половинного аргумента: six
- •2.Косинус половинного аргумента: cos
- •3.Тангенс половинного аргумента:tg X
- •Наиболее часто встречающиеся ошибки
- •Контрольный тест
- •2.Простейшие тригонометрические уравнения
- •3.Виды тригонометрических уравнений:
- •2.Однородные тригонометрические уравнения.
- •5.Некоторые другие виды тригонометрических уравнений
- •6.Уравнения, решаемые с помощью применения свойств ограниченности тригонометрических функций
- •Наиболее часто встречающиеся ошибки
- •Контрольный тест
- •Свойства обратных тригонометрических функций в таблицах(5)
- •Ответы:
- •Улучшите свои знания
- •1. Применение производной к определению промежутков монотонности
- •Решить неравенсва
- •4.Записать ответ:
- •2.Применение производной для отыскания точек экстремума
- •Используя результаты исследования, построить график.
- •5. Применение производной для нахождения наибольшего и
- •5.Выбрать из этих значений наибольшее и наименьшее.
- •6.Применение производной для определения мгновенной скорости.
- •7.Применение производной к решению геометрических задач
- •8.Уравнение касательной к графику функции f(X) в точке (x0 ; f(x0))
- •1.Записать уравнение касательной к графику функции в точке f(X) в точке (x0 ; f(x0)):
- •4.Подставить найденные значения в уравнение пункта 1.
- •Наиболее часто встречающиеся ошибки
- •1.Арифметическим корнем n- ой степени из числа a называется неотрицательное число, n- ая степень которого равна a.
- •2.Корнем n- ой степени из числа a называется число, n- ая степень которого равна a.
- •3.Свойства корней n- ой степни
- •Основные тождества
- •Наиболее часто встречающиеся ошибки
- •Контрольный тест
- •Тема 8 Степень с рациональным показателем Проверочный тест:
- •Улучшите свои знания
- •Степенью положительного числа a с рациональным показателем , m – целое, n – натуральное называется корень n- ой степени из числа a в степени m n, т.Е. .
- •2.Вычислить значение степени с рациональным показателем можно, если степень с рациональным показателем заменить корнем.
- •3.Свойства степени с рациональным показателем и положительными основаниями :
- •4.Разложение на множители
- •Контрольный тест
- •Тема 9 Показательная функция Проверочный тест:
- •Улучшите свои знания
- •6.Показательные уравнения
- •7.Показательные неравенства
- •Контрольный тест
- •Тема10 Свойства логарифмов и логарифмическая функция Проверочный тест:
- •Улучшите свои знания
- •2. Основное логарифмическое тождество:
- •3. Свойства логарифмов
- •Контрольный тест
- •Дополнительные материалы
Контрольный тест
1.Вычислите: а)log2,56,25, б)log273, в)log131, г)lg 100.
2.Вычислите: а)5Log50,5 , б)6Log648,в) 1,01Log1,010,01.
3.Вычислите:
а) log35 +log30,2; б) log310-log33⅓; в) log0,10,18.
4.Найдите область определения функци y= log0,1 (-x+3).
5. Сравните числа а) log52 и log53; б) log0,59 и log0,57;
6.Сравните с нулем числа а) log27 ;б) log0,20,15 ; в) log60,2 ;г) log0,78;
7. Определите, на каком из рисунков изображен график функции y=log3 x, а на каком – график функции y=log ⅓x?
a) б)
8.Решите уравнение:а)log0,1(3-x)=-3; б)log5 x + log5 (x-4) =1;
в) log62 x - log6 x =2;
9. Решите неравенство: а)log0,1(3-x)<-3; б)log5 x + log5 (x-4) >1;
в) log62 x - log6 x <2;
Дополнительные материалы
logarx=
 log
a x,
x>0, a>0, a
log
a x,
x>0, a>0, a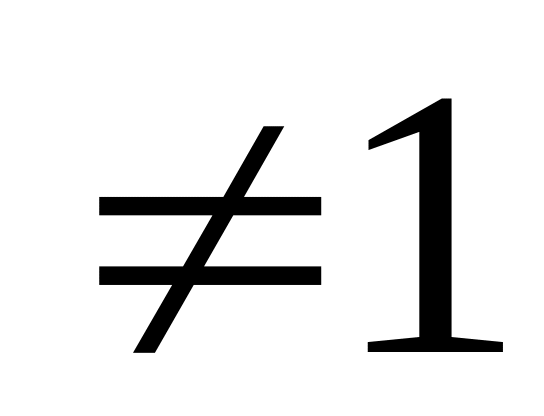 .
.
logarxr=log a x, x>0, a>0, a .
clogab = blogac, a>0, a , b>0, c>0, b , c .
(logab >0) ((a-1)(b-1)>0), a>0, a , b>0.
(logab <0) ((a-1)(b-1)<0), a>0, a , b>0.
6.
![]() ,
a>0, a
,
b>0, b
.
,
a>0, a
,
b>0, b
.
Решение логарифмических неравенств
1.Решить
неравенство:![]()
Решение
![]()
![]() x
x![]() .
.
2.Решить
неравенство:
![]()
Решение
![]()
![]()
![]()
![]()
3.Решить
неравенство:
![]()
Решение
![]()
![]()
![]()
![]()
4. Решить неравенство:
Решение
Заметим,
что выражение
![]() для
для
![]() (
(![]() ,
по свойству среднего арифметического
и среднего геометрического).
,
по свойству среднего арифметического
и среднего геометрического).
Поэтому
данное неравенство равносильно
неравенству
![]() .
.
![]()
![]() .
.
5. Решить неравенство
![]()
Решение
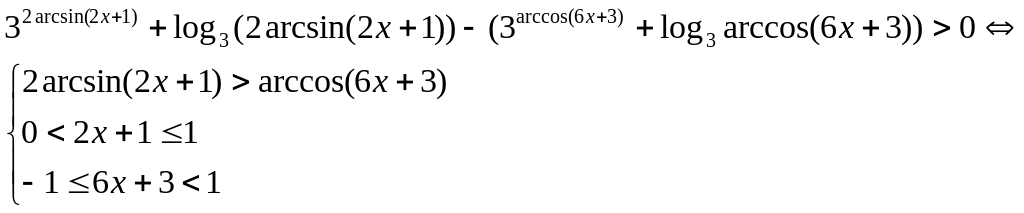
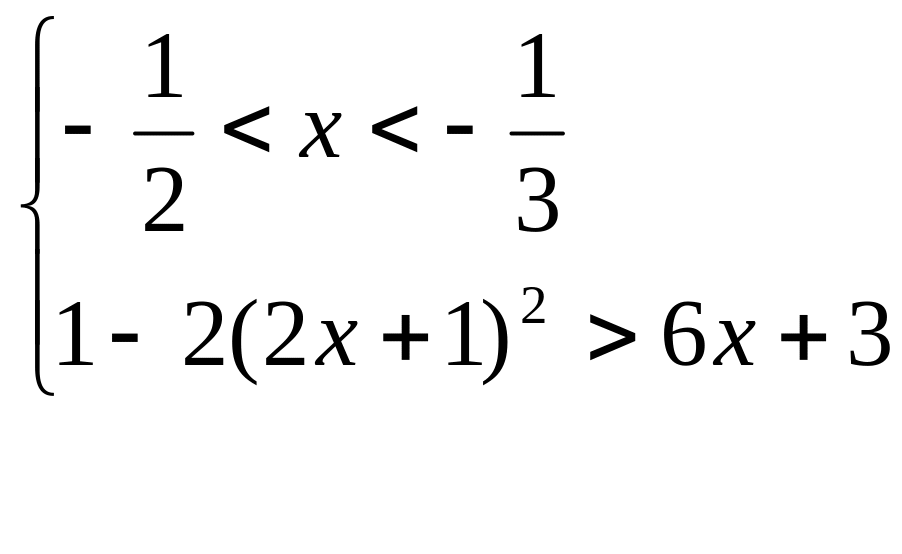
![]()
6. Найти сумму натуральных решений
неравенства
![]()
Можно решить это неравенство по аналогии с предыдущими неравенствами, используя правила замены выражений на совпадающие с ними по знаку:
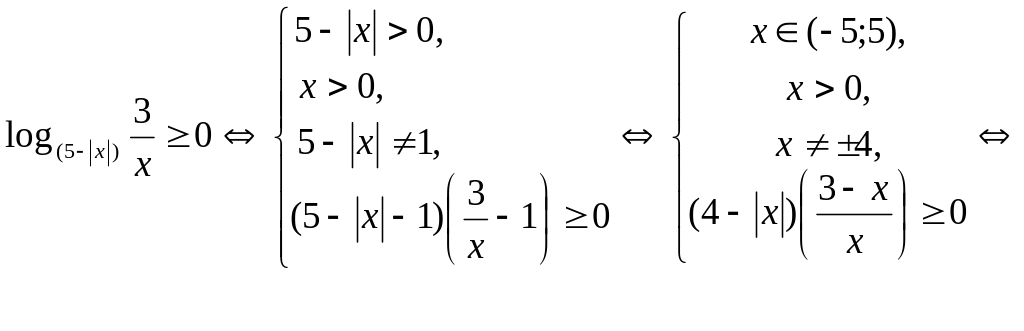
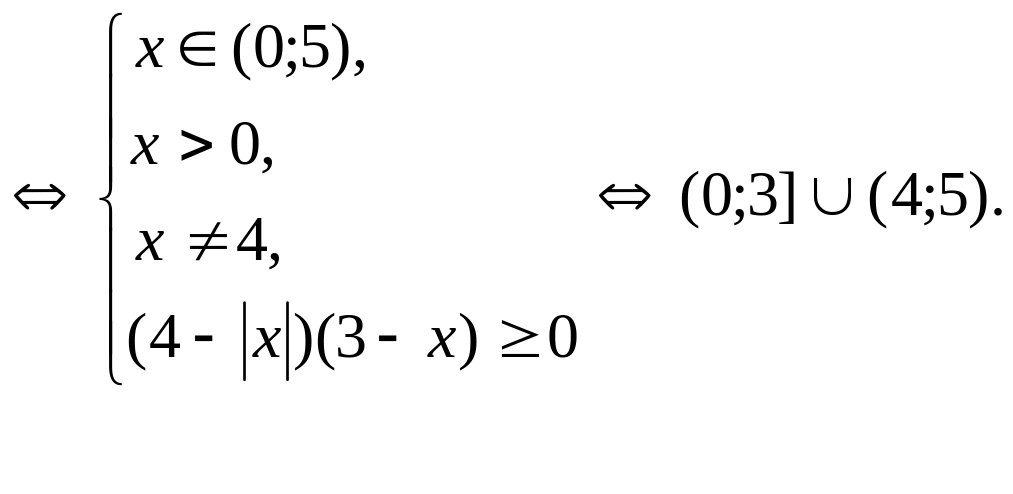
Натуральные решения 1; 2; 3. Их сумма равна 6.
Свойства логарифмов в таблице (24)
№ |
Свойство, определение |
Применение |
Примечание |
Пример |
1 |
|
Для вычисления значений логарифмов |
Можно использовать для представления числа в виде логарифма по любому основанию |
2= log9 81 |
2 |
Основное логарифмическое тождество
, b>0, a>0, a≠1.
|
Для упрощения выражений |
Можно использовать для представления любого положительного числа в виде степени с любым положительным основанием, отличным от 1 |
3= 5log5 3 |
3 |
logab + logac = logabc, где b>0, c>0, a>0, a≠ 1.
|
Для преобразований выражений, в уравнениях и неравенствах |
При переходе от левой части равенства к правой область определения может расшириться. |
log210= 1 + log25 |
4 |
logab - logac = loga (b: c), где b>0, c>0, a>0, a≠ 1.
|
Для преобразований выражений, в уравнениях и неравенствах |
При переходе от левой части равенства к правой область определения может расшириться |
lg 2=lg(10:5) 1 - g5 |
5 |
logabn =nloga b, где b>0, a>0, a≠ 1.
|
Для преобразований выражений, в уравнениях и неравенствах |
При переходе от левой части равенства к правой область определения может сузиться |
log2(x-2)4 = 4log2|x-2| |
6 |
Формула перехода от одного основания логарифма к другому logab= , где b>0, a>0, a≠ 1, с>0, c≠ 1.
|
Для преобразований выражений, в уравнениях и неравенствах |
При решении уравнений и неравенств, как правило, следует прейти к одному и тому же основанию логарифма. |
log29= .
|
7 |
Формула замены основания логарифма на его число
logab
= b ≠1,a>0, a≠ 1, |
Для преобразований выражений, в уравнениях и неравенствах |
Можно использовать неравенство |logab+ |≥2, b>0, a>0, a≠ 1,
|
log29=
|
8 |
logarx= log a x, x>0, a>0, a .
|
Для вычислений и преобразований выражений |
Для перехода к меньшему основанию логарифма |
log 4x= 1/2log 2 x, |
9 |
logarxr=log a x, x>0, a>0, a .
|
Для перехода к другому основанию логарифма, вычислений и преобразваний |
При переходе от одной части равенства к другой область определения может измениться |
|
10 |
clogab = blogac, a>0, a , b>0, c>0, b , c .
|
Для перехода к одному основанию логарифма, при вычислениях, преобразованиях, в решениях уравнений и неравенств |
Если равенство содержит переменные, то учесть область определения |
|
11 |
, a>0, a , b>0, b . |
Для перехода к одному основанию логарифма при вычислениях, преобразованиях, в решениях уравнений и неравенств |
Если равенство содержит переменные, то следует учесть область определения |
|
12 |
logab 2n =2nloga |b|, где b>0, a>0, a≠ 1.
|
Для преобразований выражений, в уравнениях и неравенствах |
Если равенство содержит переменные, то следует учесть область определения |
log4 (x-2) 2 =2log4 |x-2| |
13 |
(logab >0) ((a-1)(b-1)>0), a>0, a , b>0.
|
При решении неравенств |
Учитывать область определения |
(logx (x+4) >0) ((x-1)(x+3)>0), x>0, x , x+4>0.
|
14 |
(logab <0) ((a-1)(b-1)<0), a>0, a , b>0.
|
При решении неравенств |
Учитывать область определения |
(logx (x+4) <0) ((x-1)(x+3)<0), x>0, x , x+4>0.
|
15 |
logab - logac <0) ((a-1)(b-c)<0), a>0, a , b>0, c >0
|
При решении неравенств |
Учитывать область определения |
|
16 |
logab - logac >0) ((a-1)(b-c)>0), a>0, a , b>0, c >0
|
При решении неравенств |
Учитывать область определения |
|
17 |
logaa = 1, a>0, a , |
При решении уравнений, неравенств |
Учитывать область определения |
|
18 |
loga1 = 0, a>0, a , |
При решении уравнений, неравенств |
|
log51 = 0, log31 = 0 |
19 |
logaa n =n a>0, a , |
При решении уравнений, неравенств |
|
log55 4 =4 |
Тестовые задания: применение свойств логарифмов(25)
№ |
Задание |
Результат |
1 |
Расположите в порядке возрастания значения выражений:
|
a)-1; b) 2 ; c) ½; d)0; e) -2; f)3 e),a), d),c),b), f).
|
2 |
Представьте число 3 в виде логарифма по основанию a) 3; b) 2 ; c) ½; d) 10; e)1/3; f)a
|
a)3= log 3 27; b) 3= log 2 9; c) 3= log 1/21/8; d) 3= lg1000; e) 3= log 1/31/27; f) 3= log a a3
|
3 |
Представьте в виде степени: a) с основанием 5 число 2; b) с основанием 6 число 7; c)с основанием 4 число 9; d) с основанием 7 число 15 e) с основанием 10 число 2; f) с основанием 1/2 число 6;
|
a)
b)
c) 9 = 4log4 9; d) 15 = 7log7 15; e)
2= f)
6=
|
4 |
Найдите значение выражения
|
1)
3) 6; 4) -5/4; 5) 4;
|
5 |
|
1) ; 2) 25;3) 6; 4) -5/4;5) 4;
|
6 |
|
1) ; 2) 25; 3) 6; 4) -5/4;5) 4;
|
7 |
|
1) ; 2) 25;3) 6; 4) -5/4;5) 4;
|
8 |
|
1) ; 2) 25; 3) 6; 4) -5/4; 5) 4;
|
9 |
|
1) ; 2) 2;3) 6; 4) -5 ;5) 1;
|
10 |
|
1) ; 2) 2;3) 6; 4) -5; 5) 1;
|
11 |
|
1) ; 2) 2;3) 6; 4) -5; 5) 1;
|
12 |
|
1)0; 2) 2;3) 6; 4) -5; 5) 1;
|
13 |
|
1)0; 2) 2;3) 6; 4) -5; 5) 1;
|
14 |
|
1)9; 2) 2;3) 6; 4) -5; 5) 1;
|
15 |
Пусть
равно:
|
1)a/(a-1); 2) 1-a; 3) (1-a)/(2a); 4) 3(1+a); 5)- 1;
|
16 |
Найдите
|
1)a-2b-2/(a-1); 2) 1-a; 3) (1-a)/(2a); 4) 3(1+a); 5)- 1;
|
17 |
Найдите
|
1)a-2b-2/(a-1); 2) 1-a; 3) (1+a)/(2a+b); 4) 3(1+a); 5)- 1;
|
18 |
Пусть
Найдите: log 300 75 |
1)(a+2ab)/(2+a+2ab); 2) 1-a; 3) (1+a)/(2a+b); 4) 3(1+a); 5)- 1;
|
19 |
Пусть
Найдите:
|
1)(a+2ab)/(2+a+2ab); 2) 1-a; 3) (1+a+ab)/(2+a+ab); 4) 3(1+a); 5)- 1;
|
20 |
Известно, что
|
1)(1- 2) 1; 3) (2+ 4)
3(1+
);
5)
|
21 |
Известно, что
|
1) 2) 1- ; 3) 1; 4) 3(1+- );5) ;
|
22 |
Определите верные неравенства a) b) c)
d)
e)
f)
g)
h) |
1.b,d,g. 2.a,b,f; 3.f,g,h; 4d,e,h; 5.a,f,h |
23 |
Значение
выражения
|
1) 0; 2) 1 3)
5) -1
|
24 |
Пусть
Какое
из следующих выражений
|
1.b. 2. f; 3. h; 4d; 5.a. |
25 |
Пусть
Выражение
|
1)a/(a-1); 2) 1-a; 3) (1-a)/(2a); 4) 3(1+a); 5)- 1;
|
26 |
Результат упрощения выражения
|
1) 2 ; 2) log2x ; 3) 0; 4) ; 5) другой ответ |
Свойства логарифмической функции(26)
Свойства функция |
y = lоga x , a >1 |
y = lоga x , 0 <a < 1 |
Область определения (D) |
D(lоga x) =(0;+ ∞)
|
D(lоga x) =(0;+ ∞)
|
Множество значений (E) |
E(lоga x) =(- ∞;+ ∞)
|
E(lоga x) =(- ∞;+ ∞) |
Нули функции |
lоga x =0 x=1 |
lоga x =0 x=1 |
Знаки функции |
logax > 0 при x>1 logax < 0 при 0<x<1.
|
logax<0 при x >1 logax >0 при 0<x<1.
|
Промежутки возрастания |
y = lоga x при a>1 возрастает на всей области определения.
|
|
Промежутки убывания |
|
y = lоga x при 0<a<1убывает на всей области определения.
|
Графики |
|
|
Тестовые задания на применение свойств логарифмической функции(27)
№ |
Задание |
Ответ |
1 |
Найдите область определения функции y=log3 (5 + 4x - x2 )
|
1.(-1;5); 2. [-1;5); 3. [-1;5]; 4.(-∞;-1) (5;+∞) 5. .(-∞;-1] [5;+∞) |
2 |
Найдите область определения функции y= logx+1 (2-x)
|
1.(-1;2); 2. [-1;0); 3. [-1;2]; 4.(-1;0) (0;2) 5. .(-∞;-1] [2;+∞) |
3 |
Найдите множество значений функции y=log3 (5 + 4x - x2 )
|
1.(-1;2); 2. [-1;0); 3. [-1;2]; 4.(-1;0) (0;2) 5. (-∞;2] |
4 |
Наибольшее значение функции y=log3 (2+ 2x - x2 )
|
1)0;2)4;3)2;4)1; 5)1/9.
|
5 |
Наименьшее значение функции y=log0,5 (3+ 2x - x2 )
|
1)0;2)4;3)-2;4)1; 5)1/4.
|
6 |
Больше единицы значение функции
|
1)64;2)4;3)2;4)1; 5)1/16.
|
5 |
Больше единицы значение функции
|
1)64;2)4;3)2;4)1; 5)1/16.
|
6 |
Только неотрицательные значения принимает функция: |
1.y=log1/3 (5 + 4x - x2 ); 2. y=log3 (5 + 4x + x2 ); 3. y=log3 (3 + 4x -x2 ); 4. y=log1/3 (3 + 4x -x2 ); 5. y=log1/2 (3 + 4x -x2 ). |
7. |
Решите уравннеие
|
1)0;2)4;3)3;4)1; 5)1/9.
|
8. |
Решите уравннеие
|
1)0;2)4;3)3;4)1; 5)1/9.
|
9. |
Решите уравннеие
|
1)2;2)4;3)3;4)1; 5)1/9.
|
10 |
Решите неравенство
|
1. (1;7) (7;+∞); 2. [1;7); 3. [1;2]; 4.(1;7) (7;79) 5. .(-∞;-1] [7;+∞) |
11 |
Решите неравенство
|
1)0;2)4;3)-2;4)-1; 5)1/9. |
12 |
Решите уравннеие
|
1)0;2)π;3)3 π;4)1; 5)3. |
13 |
Решите уравннеие
|
1)0;2)π;3)3 π;4)1; 5)3. |
14 |
Решите уравннеие
|
1)0;2)π;3)4 ;4)1; 5)3 |
15 |
Решите уравннеие
|
1)0;2)π;3)3 π;4)1; 5)3. |
16 |
Решите уравннеие
|
1)0;2)π;3)3 π;4)1; 5)3. |
17 |
Решите уравннеие
|
1)0;2)2;3)3 π;4)1; 5)3. |
18 |
Корень уравнения
|
1) (-3;1] ; 2) [-1;2 ); 3) (-10;0]; 4 ) (-10;3]; 5) [0;3 ) |
19 |
Наименьший корень уравнения
равен
|
1) -2; 2) -0,5; 3) π/2; 4) 8; 5) другой ответ
|
20 |
Наименьшее неотрицательное число из области определения функции
y =
|
1).1 ;2) π; 3) 2; 4) 2π; 5) 0.
|
Решние логарифмических уравнений и неравенств в таблицах(28)
№ |
Вид уравнения, неравенства |
Метод решения |
Применение |
Примечание |
|
1 |
loga f(x)= loga g(x)
а>0, а≠1 |
loga f(x)= loga g(x) , где а>0, а≠1, g(x) > 0, f(x) > 0. |
Применяется для любого положительного основания, отличного от 1. |
При решении уравнения могу появиться посторонние корни, поэтому следует сделать проверку решений. |
|
2 |
loga f(x)= = b где а>0, а≠1 |
loga f(x)= = b f(x)=a b |
Применяется для любого положительного основания, отличного от 1. |
|
|
3 |
A loga 2 f(x) +B loga f(x)= +C=0 , A≠0. |
С помощью подстановки y= loga f(x) сводится к квадратному уравнению Ay2+By+C=0. |
Применяется для уравнений, содержащих loga 2 f(x) и loga f(x) или loga f(x) и loga -1 f(x) . |
Подстановка может быть применена к уравнению p(x)= loga f(x)
|
|
4 |
Уравнения, решаемые функциональным методом |
f(x)= g(x) |
Если f(x) возрастает, а g(x) не возрастает на их общей области определения, то уравнение f(x)= g(x) имеет не более одного корня. |
Так как
|
|
5 |
Уравнения, решаемые методом логарифмирования |
Переменная величина под знаком логарифма и в основании степени |
При условии, что обе части уравнения положительны, обе части уравнения можно логарифмировать |
Область определения:
|
|
6. |
loga f(x)>
>loga g(x),
а>0, а≠1; loga f(x)<
<loga g(x)
а>0, а≠1 |
Применить замену данного выражения на знакосовпадающее с ним |
Применяется для решения неравенств, содержащих переменную в основании |
|
|
7. |
A loga 2 f(x) +B loga f(x) +C >0 , A≠0. A loga 2 f(x) +B loga f(x) +C <0 , A≠0. |
С помощью подстановки y= loga f(x) сводится к квадратному неравенству Ay2+By+C>0. ( Ay2+By+C<0) |
Применяется для неравенств содержащих loga 2 f(x) и loga f(x) или loga f(x) и loga -1 f(x) . |
log72 x + log7 x < 6; Обозначим log7 x через t, log7 x =t, тогда неравенство примет вид t2 + t<6; откуда -3<t<2. Учитывая то, что log7 x =t, получим неравенство -3<log7 x<2, 1/343<x <49. Решением данного неравенства служит промежуток (1/343;49) |
|
Тестовые задания: простейшие логарифмические уравнения и неравенства (29)
№ |
Задание |
Ответы |
1 |
Решите уравнение
|
1)
;
2)2; 3); 4)0; 5) |
2 |
Решите уравнение
|
1) ; 2)2; 3); 4)0; 5) . |
3 |
Решите уравнение
|
1) ; 2)2; 3); 4)-5; 5) . |
4 |
Число корней уравнения
|
1)5; 2)2; 3)7; 4)0; 5)6 . |
5 |
Число корней уравнения
|
1)3; 2)2; 3)7; 4)0; 5)6 . |
6 |
Число корней уравнения
|
1)5; 2)2; 3)7; 4)0; 5)6 . |
7 |
Решите уравнение
|
1.-0,5; 2,5; 2)2;3; 3)-7;1; 4)0;0,5 5)-2;2,5 . |
9 |
Решите уравнение
|
1)3; 2)2; 3)7; 4)0,5 5)6 . |
9 |
Решите уравнение
|
1.-3,25; 1,25; 2)2;3; 3)-7;1; 4)0;0,5 5)-2;2,5 . |
10 |
Решите уравнение
|
1)3; 2)2; 3)7; 4)0,5 5)6 . |
11 |
Решите уравнение
|
1)3; 2)2; 3)0; 4)0,5 5)6 . |
12 |
Число корней уравнения
|
1)3; 2)2; 3)1; 4)0; 5)4 . |
13 |
Решите уравнение
|
1)10; 2)2; 3)1; 4)100; 5)0,1 |
14 |
Число корней уравнения
|
1)3; 2)2; 3)1; 4)2; 5)0 |
15 |
Решите уравнение
|
1. |
16 |
Число корней уравнения
|
1)3; 2)2; 3)1; 4)4;5)0. |
17 |
Число корней уравнения
|
1)3; 2)2; 3)1; 4)0; 5)4 . |
18 |
Число целых рашений неравенства: |
1)3; 2)2; 3)1; 4)0; 5)4 . |
19 |
Наибольшее целое решение неравенства: |
1)10; 2)2; 3)100; 4)99; 5) 1000 |
20 |
Число целых решений неравенства
|
1)3; 2)2; 3)1; 4)4;5)0. |
Тестовые задания логарифмические уравнения и неравенства (30)
№
|
Задание |
Ответы |
1 |
Решите уравнение log1/3(3+│sin x │) =2│x│-2 |
1)π; 2)2π; 3) π +2πn,n Z; 4)0; 5) πn,n Z. |
2 |
Решите уравнение
log22x + (x-1) log2x = 6-2x
|
1)0,25; 2; 2)1 ; 1; 3) 2; 1; 4) 2; 2; 5)0,25;1. |
3 |
Решите уравнение
log22
(x+y)
– 2sinx
│y-1│=0
|
1)1; 2; 2)1 ; 1; 3) 2; 1; 4) 2; 2; 5)0,25;1. |
4 |
Решите уравнение
3sin x
=
|
1)- 2)2π; π;3) π +2πn, π +2πn, n Z; 4)0; 0;5) πn,πn,n Z. |
5 |
Решите уравнение: log2 (4x+1) log5 (4x+4)+ +log3 (4x+2) log4 (4x+3) = 2 log3 (4x+2) log5 (4x+4)
|
1)¼. 2)1 ; 3) 2; 4) 2; 5)0,25;
|
6 |
Решите неравенство:
|
1.(1;7) 2)(1 ; +∞) 3) (7 ; +∞) 4) [1 ; +∞); 5) [7 ; +∞)
|
7. |
Определите количество решений уравнения
|
1.4; 2.3; 3.5; 4.9; 5.1. |
8 |
Решить неравенство:
|
1. 2.
3.[ 0;3] (4;5); 4.
5.
|
9 |
Решить неравенство:
|
1. ; 2. 3.[0;3] (4;5); 4. ; 5. |
10 |
Решите неравенство:
|
1. ; 2. ; 3.[ 0;3] (4;5); 4. ; 5. |
11 |
Решите неравенство:
|
1.[1;3] 2. ; 3.[ 0;3] (4;5); 4. ; 5. |
12 |
Решите неравенство:
|
|
13 |
Решите неравенство:
|
1. ; 2. ; 3.[ 0;3] (4;5); 4. ; 5. |
14 |
Решите неравенство:
|
|
15 |
Решите неравенство: |
1. 2. ; 3.[0;3] (4;5); 4. ; 5.
|
16 |
Решите неравенство:
|
1. ; 2. ; 3.[0;3] (4;5); 4. ; 5.
|
17 |
Найдите сумму целых решений неравенства
|
1.4; 2.3; 3.5; 4.9; 5.1. |
18 |
Решите неравенство:
|
1) 2.
3.
4.
5.
|
19
|
Решите неравенство:
|
1) ; 2. 3. ; 4. ; 5.
|
20 |
Решите неравенство:
|
1) ; 2. ; 3) 4. ; 5. |
21 |
Решите неравенство:
|
1) ; 2. ; 3) ; 4. 5.
|
22
|
Решите неравенство:
|
1) ; 2. ; 3) ; 4. ; 5. |
23
|
Решите неравенство:
|
1. 2. ; 3) ; 4. ; 5. |
24 |
Определите число целых решений неравенства log2+x (6-│x│) ≥ 0 |
1) 6; 2.3; 3.5; 4.9; 5.1. |
25 |
Решите уравнение
|
1.8, π/2; 5π/2. 2. 4, 5π/2. 3. π/2; 5π/2. 4. 5π/2. 5. 2, π/2. |
26 |
Решите уравнение: log9(37-12x)·log7-2x3 = 1.
|
1.1; 2.3; 3.5; 4.2; 5.-1. |
27 |
lg sinx + lg cosx < 0
|
1.(2πn;π/2+2πn), n 2. (4; 5π/) 3. (π/2; 5π/2). 4. 5π/2. 5.(1;π/2). |
Дополнительные справочные материалы
29
Данное выражение |
Выражение, совпадающее по знаку с данным |
Дополнительные условия |
|
|
|
|
|
, |
|
|
|
|
|
, , |
|
|
, |
|
|
— |
|
|
|
|
|
— |
|
|
|
|
|
|
|
|
|
|
|
— |
30
Название формулы |
Вид формулы |
Применение |
Разность квадратов |
a2 - b 2 = (a-b)(a+b) |
Для разложения выражения на множители. |
Квадрат разности |
(a - b) 2 = a 2 -2ab + b 2 |
В тождественных преобразованиях. |
Квадрат суммы |
(a + b) 2 = a 2 +2ab + b 2 |
В тождественных преобразованиях. |
Куб разности |
(a - b) 3 = a 3 -3a 2b +3a b 2 –b3 |
В тождественных преобразованиях. |
Куб суммы |
(a + b) 3 = a 3 +3a 2b +3a b 2 +b3 |
В тождественных преобразованиях. |
Разность кубов |
a3 - b 3 = (a-b)(a 2 +ab+b 2) |
Для разложения выражения на множители. |
Сумма кубов |
a3 + b 3 = (a+b)(a 2 -ab+b 2) |
Для разложения выражения на множители. |
Квадрат суммы трех выражений |
(а + b + c)2 = a2 + b2 + c2 + 2ab +2ac +2bc. |
В тождественных преобразованиях многочленов. |
Куб суммы трех выражений |
(а + b + c)3 = a3 + b3 + c3+ 3a2b +3ab2 +3a2c +3ac2 +3c2b +3cb2 +6abc.
|
В тождественных преобразованиях. |
Разность n- ых степеней |
аn - bn
= (a-b)(an-1+
an-2b+…+
abn-2
+bn-1),
|
В тождественных преобразованиях. |
Сумма n- ых степеней |
аn + bn = (a + b)(an-1- an-2b +…+ abn-2 - bn-1), , n- нечетное число.
|
В тождественных преобразованиях. |
Формула корней квадратного уравнения
|
Если
|
Для решения квадратных уравнений относительно функции f(x) |
Формула корней квадратного уравнения с четным вторым коэффициентом
|
Если
|
При решении квадратных уравнений со вторым четным коэффициентом |
Сумма n первых натуральных чисел |
1 +2 +3+…+ n = n(n+1)/2;
|
В тождественных преобразованиях |
Сумма квадратов n первых натуральных чисел |
12 +22 +32+…+ n2 = n(n+1)(2n+1)/6;
|
В тождественных преобразованиях |
Сумма кубов n первых натуральных чисел |
13 +23 +33+…+ n3= ( n(n+1)/ 2)2;
|
В тождественных преобразованиях |
Формула n- ого члена арифметической прогрессии |
|
Для вычисления n- ого члена прогрессии, номера члена, разности прогрессии |
Формула n- ого члена геометрической прогрессии |
|
Для вычисления n- ого члена прогрессии, номера члена, знаменателя прогрессии |
Формула суммы n первых членов арифметической прогрессии |
Sn
=
|
Для вычисления суммы n членов прогрессии можно использовать формулу
|
Формула суммы n первых членов геометричской прогрессии |
|
Для вычисления суммы n членов прогрессии можно использовать формулу
|
Характеристическое свойство арифметической прогрессии |
Для того чтобы числовая последовательность была арифметической прогрессией, необходимо и достаточно, чтобы каждый ее член, начиная со второго, был равен среднему арифметическому соседних с ним членов.
|
|
Характеристическое свойство геометрической прогрессии |
Для того чтобы числовая последовательность была геометрической прогрессией, необходимо и достаточно, чтобы каждый ее член, начиная со второго, был равен среднему геометрическому соседних с ним членов.
|
|
Формула суммы бесконечно убывающей геометрической прогрессии |
S =
|
Для вычисления суммы бесконечно убывающей геометрической прогрессии, для представления бесконечной десятичной дроби в виде обыкновенной. |
Дополнительные сведения.
НОД(a;b)- наибольший общий делитель двух натуральных чисел –
это наибольшее число, на которое делится и число a, и число b.
НОК(a;b)- наименьшее общее кратное двух натуральных чисел –
это наименьшее число, которое делится и на число a, и на число b.
a·b = НОД(a;b)· НОК(a;b).
Признаки делимости
1.Для того, чтобы число делилось на 3(9), необходимо и достаточно, чтобы сумма цифр этого числа делилась на 3(9) .
2.Для того, чтобы число делилось на 5, необходимо и достаточно, чтобы последняя цифра этого числа была 0 или 5.
3.Для того, чтобы число делилось на 4, необходимо и достаточно, чтобы последние две цифры этого числа образовывали число, делящееся на 4.
4.Для того, чтобы число делилось на 11, необходимо и достаточно, чтобы разность между суммами цифр, стоящих на четных и нечетных местах делилась на 11.
5. Для того чтобы число делилось на 7, 11,13, необходимо и достаточно, чтобы разность между числом, записанным тремя последними цифрами, и числом, записанным всеми остальными цифрами, делилась на 7, 11,13.
Правило обращения обыкновенной дроби в десятичную
Если разложение знаменателя десятичной дроби на простые множители содержит только числа 2 или 5, то дробь обращается в конечную десятичную дробь. Во всех других случаях – в бесконечную периодическую.
Бесконечную периодическую дробь можно записать в виде обыкновенной по правилу:
бесконечная десятичная периодически дробь равна обыкновенной дроби, в числителе которой разность между числом, записанным цифрами
числа после запятой до второго периода и числом, записанным цифрами числа до первого периода; в знаменателе – число, в котором сначала записывается столько девяток, сколько цифр в периоде, а затем – столько нулей, сколько цифр после запятой до первого периода.
Примеры
2, 5(6) =
![]()
15, 456(38) =![]() .
.
Ответы к контрольным тестам.
Тема 1
а) х ≠ π/2 +πk , k – целое число; х≠-1/2 ; х ≠ π/12 +π/3 k , k – целое число;
б) [-2; 2]; [2/3; 4/3]; [-0; +∞) .
а) 2π/11; б)1/2; в)5π.
четная функция – tg x2 ; нечетная функция - xcosx ; не является ни четной функцией, ни нечетной – sin(x+1).
а)“плюс”; б) “плюс”.
а) sin 10π /9; sin π/12; sin 2,1 π; б) cos1,4 π; cos2,3 π; cos π/5; в) tgπ/7; tg2,9 π; tg4π.
б)
Тема 2
1.![]() ;
2.
;
2.![]() ;
3. tgα;
4.
;
3. tgα;
4.![]() .
.
Тема 3
1.
π/4. 2. а)(-1)kπ/6
- π/4 + πk; k
Z.б)
arctg2 + πk, k
Z.
в)
![]()
3.
а)
- π/2+ 2πk, k
Z.
б)
-![]() ;
(-1)k
аrcsin0,2+
;
(-1)k
аrcsin0,2+
в)
![]()
Тема 4
1.а)
-![]() +12x2;
б)
+12x2;
б)
![]() в)
в)
![]() – 1; г) 7x6+8x3-3x2;
2. 160;
– 1; г) 7x6+8x3-3x2;
2. 160;
3. x<7;
Тема 5
1. На промежутках (- ; 0) и ( ; ) функция убывает, на промежутке
(0; ) функция возрастает; x= – точка максимума.
2.
3. Наибольшее значение функции равно -0, наименьше значение функции
равно -2.
4. в точке x=1: y=2x-2; в точке х=-1: y=-2x+2.
Тема 6
1.y=-cosx+2,5; 2. -π/6; 3.а)38; б)2√3 – 2/3; в)1.
Тема 7
1. а) 7; б)6,8; -6,8; в)![]() ;
-
;
г)
;
2.0; 3. первое больше;
;
-
;
г)
;
2.0; 3. первое больше;
Тема 8
1. -2; 2. 8; 3. x+x0,5+x-0,5+1;
Тема 9
1.а)
x=-![]() ;
б) x
=6; в) x=1;
2. а) x
<-
;
б) x
>6; в) x>1;
3. а)0; 1; б) 0; 4. а) (0;1); б) x>0.
;
б) x
=6; в) x=1;
2. а) x
<-
;
б) x
>6; в) x>1;
3. а)0; 1; б) 0; 4. а) (0;1); б) x>0.
Тема 10
1.а)2; б) ; в)0; г)2; 2.а)0,5; б)48; в) 0,01; 3. а) 0; б) 2; в) 8; 4. (-∞;3);
5. а) log52 < log53; б) log0,59 < log0,57; 6.а) log27>0 ;б) log0,20,15>0 ;
в) log60,2<0 ; г) log0,78<0; 7. а) y=log ⅓x; б) у=log3 x;
8. а) -997; б)5; в) 36; 9. а) (-∞;-997); б) (5; +∞); в) (36; +∞);

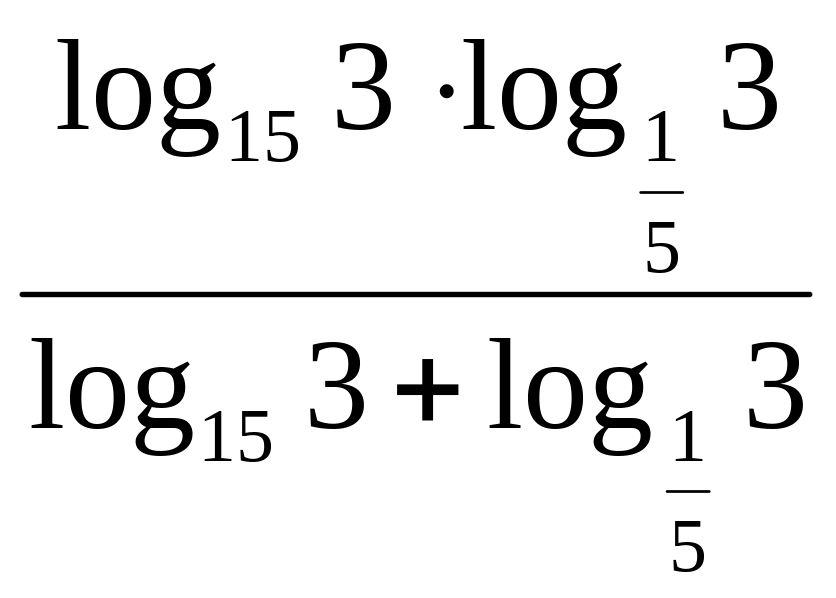 равно:
равно: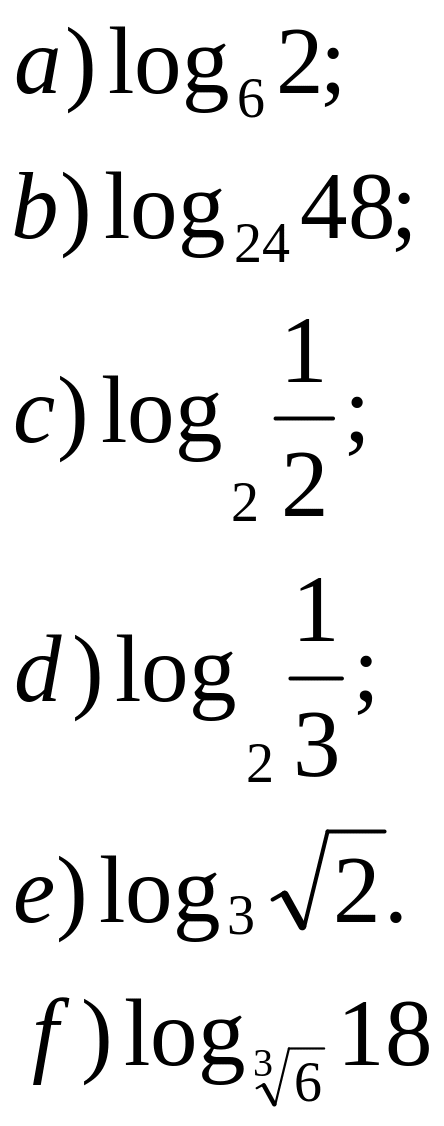 равно 3(1+a)?
равно 3(1+a)?