Тема10 Свойства логарифмов и логарифмическая функция Проверочный тест:

1.Вычислите: а)log₂16, б)log₅125, в)log_0,50,25, г)log₃1.

2.Вычислите: а)4^Log₄⁷ , б)8^Log₈⁷, в) 0,1^Log_0,1⁷.

3.Вычислите:

а) log₂⅔ +log₂1,5; б) log₂3-log₂1,5; в) log₄4⁵.

4.Найдите область определения функци y= log₂ (x-6).

5. Сравните числа а) log₃5 и log₃7; б) log_0,35 и log_0,37;

6.Сравните с нулем числа а) log₃5; б) log_0,30,4 ; в) log₇0,1 ;г) log_0,64;

7. Определите, на каком из рисунков изображен график функции y=log₂ x, а на каком – график функции y=log_0,5 x?

a)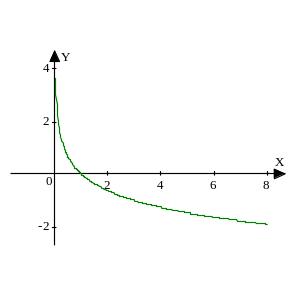 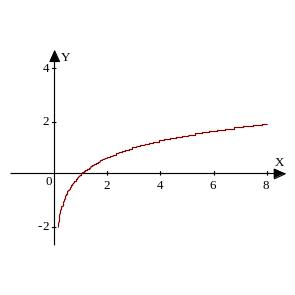b)

8.Решите уравнение:а)lg(3-x)=-1; б)log₃ x + log₃ (x-2) =1;

в) log₇² x + log₇ x =6;

9. Решите неравенство: а)lg(3-x)< -1; б)log_0,5 x + log_0,5 (3-x) <-1;

в) log₇² x + log₇ x <6;

Ответы:

1.а) 4;б)3;в)2;г)0. 2.а)7;б)7;в)7; 3.а)0;б)1;в)5. 4.(6;+∞). 5. а) log₃5 <log₃7;

б) log_0,35 >log_0,37. 6. а) log₃5>0 ;б) log_0,30,4>0 ; в) log₇0,1<0 ;г) log_0,64<0.

7.a) log_0,5 x.b) log₂ x 8.а)2,9; б)3; в)343; 1/49. 9.а)(- ∞; 2,9); б)(1;2); в)(1/343; 49).

Улучшите свои знания

1.Логарифмом числа b по основанию a, где b>0, a>0, a≠ 1, называется показатель степени, в которую нужно возвести число a, чтобы получить число b.

Например, log₂16=4, так как 2⁴=16, log₃9=2, так как 3² = 9.

Обозначение: log_ab, читается: логарифм числа b по основантю a.

Если основание a равно 10, то логарифм называется десятичным и обозначается lgb, если основание равно числу e, то логарифм называется натуральным и обозначается lnb.

Например, lg100 =2 , так как 10²=100, lg0,1 = -1, так как 10 ^-1=0,1 lne=1, так как e¹=e.

2. Основное логарифмическое тождество:

, b>0, a>0, a≠1.

Например, 4^Log₄⁷ =7; 8^Log₈⁷ =7; 0,1^Log_0,1⁷=7.

3. Свойства логарифмов

а) log_ab + log_ac = log_abc, где b>0, c>0, a>0, a≠ 1.

Например, log₂⅔ +log₂1,5= log₂ (2/3)∙(1,5) = log₂1=0.

б) log_ab - log_ac = log_a (b:c), где b>0, c>0, a>0, a≠ 1.

Например, log₂3-log₂1,5= log₂ (3:1,5) = log₂2 =1.

в) log_abⁿ =nlog_a b, где b>0, a>0, a≠ 1.

Например, log₄4⁵ =5 log₄4 =5∙1=5.

г) формула перехода от одного основания логарифма к другому

log_ab= , где b>0, a>0, a≠ 1, с>0, c≠ 1.

Например, log₂9= .

Основные свойства логарифмов

,

, , , ,

4. Функция, заданная формулой y = lоg_a x , a>0, a≠1 логарифмической.

D(lоg_a x) =(0;+ ∞)

E(lоg_a x) =(- ∞;+ ∞)

Например, найдите область определения функции y= log₂ (x-6).

Решение: так, как область определения логарифмической функции есть промежуток (0; +∞) , то функция y= log₂ (x-6) определена для всех значений x, для которых выполняется условие: x-6>0, откуда получим

x>6, x (6;+∞). Oбласть определения функции y= log₂ (x-6) есть промежуток (6;+∞).

5 .Если основание логарифмической функции y = lоg_a x больше 1, то она возрастает на всей области определения.

Если основание логарифмической функции y = lоg_a x больше нуля, но меньше 1, то она убывает на всей области определения.

Например, cравните числа а) log₃5 и log₃7; б) log_0,35 и log_0,37;

Решение

а) log₃5 <log₃7, так как основание логарифмической функции y= log₃x

3>1, то логарифмическая функция возрастает на области определения, значит, так как 5<7, то log₃5 <log₃7;

б) log_0,35 и log_0,37; так как основание логарифмической функции y= log _0,3x

3>1, то логарифмическая функция убывает на области определения, значит, так как 5<7, то log₃5 >log₃7.

6.Если a>1, то log_ax>0 при x>1 и log_ax <0 при 0<x<1.

Если 0<a<1, то log_ax<0 при x>1 и log_ax >0 при 0<x<1.

Если x=1, то, log_ax=0 для любого положительного основания a.

Например, сравните с нулем числа а) log₃5 ;б) log_0,30,4 ; в) log₇0,1 ;

г) log_0,64;

Решение

а) log₃5>0, так как основание логарифмической функции y= log₃x

3>1 и x=5 >1.

б) log_0,30,4 >0, так как основание логарифмической функции y= log _0,3x

0,3<1 и x=0,4 <1.

в) log₇0,1<0, так как основание логарифмической функции y= log₇x

7>1 и x=0,1 <1.

г) log_0,64<0, так как основание логарифмической функции y= log _0,6x

0,6<1 и x = 4 >1.

7. График функции y= log_ax a>1 изображен на рисунке:

График функции y= log_ax 0<a<1 изображен на рисунке:

8.Уравнение log_a f(x)= log_a g(x) равносильно уравнению, a>0? a≠1, f(x)= g(x),при дополнительных условиях g(x) > 0, f(x) > 0.

Например, решите уравнение а)lg(3-x)=-1; б)log₃ x + log₃ (x-2) =1;

Решение

а)lg(3-x)=-1, представим -1в виде -1=lg0,1, тогда lg(3-x)= lg0,1, откуда

3-x=0,1,т.е. x=2,9. Проверим, 3 - 2,9 = 0,1>0.

Ответ: 2,9.

б)log₃ x + log₃ (x-2) =1.

По свойству логарифмов 3а) будем иметь log₃ x (x-2) =1, далее x (x-2)=3

( log₃ 3=1), x² -2x-3 =0, корни этого уравнения x=3 , x=-1.

Проверим x=3>0, x-2=3-2>0, значит 3 – корень данного уравнения.

Проверит x=-1<0, значит -1 – не корень данного уравнения.

Ответ: 3.

в)При решении логарифмических уравнений используется метод введения новой переменной

Например, решите уравнение: log₇² x - log₇ x =6

Решение

Обозначим log₇ x=y, получим y² + y=6, откуда y² -y - 6 =0, корни этого

уравнения y= 3, y=-2.

Вернувшись к введенным обозначениям, получим: log₇ x=3, log₇ x=-2.

Решая последние два уравнения, получим: x=343,x= 1/49.

Ответ: 343; 1/49.

9.Неравенство log_a f(x)> log_a g(x) равносильно неравенству f(x)> g(x),при

a>1 и дополнительных условиях g(x)>0, f(x)>0.

Неравенство log_a f(x)> log_a g(x) равносильно неравенству f(x)< g(x),при

0<a<1 и дополнительных условиях g(x)>0, f(x)>0.

Например, решите неравенство:

а)lg(3-x)< -1;

Решение

Неравенство lg(3-x)< -1 равносильно системе:

решая каждое неравенство системы, получим: или или

x .

Ответ:

б) log_0,5 x + log_0,5 (3-x) <-1;

Неравенство log_0,5 x + log_0,5 (3-x) <-1 равносильно системе: или или .

Первое неравенство решим методом интервалов, получим 1<x<2,

тогда система будет иметь вид .

Решение этой системы промежуток (1;2).

Ответ: (1;2).

в) log₇² x + log₇ x < 6;

Решение

Обозначим log₇ x через t, log₇ x =t, тогда неравенство примет вид

t² + t<6; откуда -3<t<2.

Учитывая то, что log₇ x =t, получим неравенство -3<log₇ x<2,

1/343<x <49. Решением данного неравенства служит промежуток (1/343;49).

Наиболее часто встречающиеся ошибки:

!Проверь, не делаешь ли ты так!

1. Из неравенства log_0,5x<log_0,57 не следует неравенство x<7!

Правильно будет x>7, так как логарифмическая функция с основанием 0,5 убывающая.

2. lg3+lg2≠lg5. Правильно будет: lg3+lg2=lg(3∙2)=lg6.

3. lg6 –lg2≠lg4. Правильно будет: lg6-lg2=lg(6:2)=lg3.

4. lg x² ≠2lg x. Правильно будет: lg x² =2lg|x|.