Тема 9 Показательная функция Проверочный тест:
1. Найдите
с точностью до десятых значение функции
y =
при x=
2.Сравните с нулем числа:
а)
0,0
;б)
;
в) 7,40,11;
г)125,34-34.
3. Сравните числа:
а) (1,2)-15 и (1,2)-14;
б) (0,131)2,4 и (0,131)1,8;
в)
и
.
4. Сравните с единицей числа:
а)0,0 ;б) ; в) 7,40,11; г)125,34-34.
5.
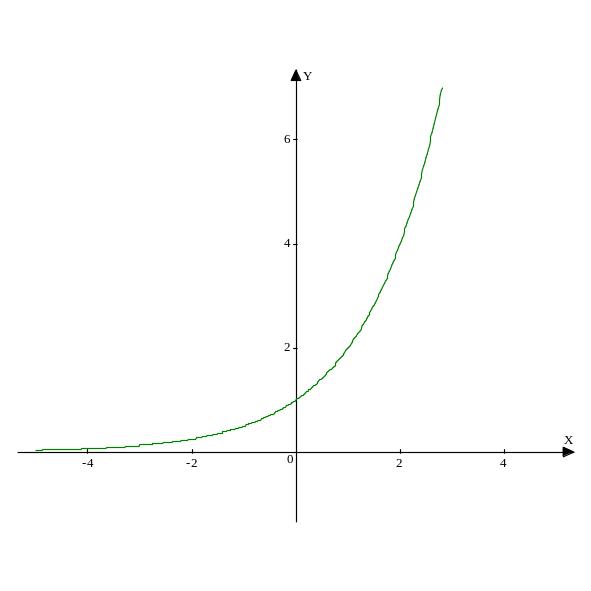
На рисунке изображен график функции
.
Сравните a
c
единицей.
а)
;
б).
6. Решите уравнение:
а)33x-2 =36-x; б) 9x -8∙3x - 9 =0.
7.Решите неравенство:
а) 0,2x >0,04; б) 7x-3 < 49.
Ответы:
1. 2,7.
2.а) 0,0 >0;б) >0; в) 7,40,11 >0; г)125,34-34>0.
3.а) (1,2)-15 <(1,2)-14;б) (0,131)2,4 < (0,131)1,8;в) < .
4.а)0,0 >1;б) >1; в) 7,40,11>1; г)125,34-34<1.
5.а)0<a<1; б)a>1. 6.а)2; б) 2; 7а)(- ∞;2); б) (- ∞;5).
Улучшите свои знания
Функция, заданная формулой
y
=
,
где a>0,
x
R
называется показательной.
Свойства показательной функции
1. D( )=(-∞; +∞), это означает, что для любого положительного a и любого действительного x можно найти .
Например,
вычисляется через десятичные приближения
числа
с любой степенью точности. 1,4142<
<1,
4143,
.
Найдем с помощью калькулятора
21,4142
2, 6651, 21,4143
2, 66530,
Значит, =2,665…
2.E(ax )=( 0, +∞), это означает, что функция y=ax для любого положительного a и любого действительного x принимает только
положительные значения.
Например, 0,0 >0; >0; 7,40,11 >0; 125,34-34>0.
3.Если основание показательной функции y= ax больше 1, то она возрастает на всей области определения.
Если основание показательной функции y= ax больше нуля, но меньше 1, то она убывает на всей области определения.
Например, значение функции y=1,2x (a=1,2>1) при x= -15 меньше, чем ее значение при х= -14, а , значение функции y=0,131x (0<a<1) при x= 2,4 меньше, чем ее значение при х =1,8
(1,2)-15 <(1,2)-14; (0,131)2,4 < (0,131)1,8.
4.Если a>1, то ax >1 при x>0 и 0<ax <1 при x<0.
Если 0<a<1, то ax <1 при x>0 и 0<ax <1 при x>0.
Если a=0, то ax =1, для любого положительного основания a.
Например, 0,0 >1(a=0,04<1, x= -2<0) ; >1(a= 2/7<1, x=-0,6<0) ; 7,40,11>1(a=7,4>1, x=0,11>0) ; 125,34-34<1(a=125,34>1 , x=-34<0).
5.На рис. изображен график функции y=ax для a>1.
На рис. изображен график функции y= ax для 0< a<1.
6.Показательные уравнения
а) уравнение вида af(x)=ag(x),где а>0, а≠1 сводится к решению уравнения
f(x) = g(x).
Например, уравнение 33x-2 =36-x равносильно уравнению 3x-2=6- x
(функция y=3t возрастающая и равным значениям функции соответствуют равные значения аргумента), далее: 4x=6+2, 4x=8, x=2.
б) уравнение Aa2x+Bax+C=0 c помощью подстановки y=ax сводится к квадратному уравнению Ay2+By+C=0.
Например, решить уравнение:
9x -8∙3x - 9 =0.
9x -8∙3x - 9 =0, 32x -83x -9=0, пусть 3x =y, тогда данное уравнение будет иметь вид: y2 -8y – 9=0. Найдем корни этого уравнения, получим: y=9 или
y=-1.Cледовательно, 3x =9 или 3x =-1. Уравнение 3x =9 имеет один корень, равный 2, уравнение 3x =-1 не имеет решений.
Ответ: 2.