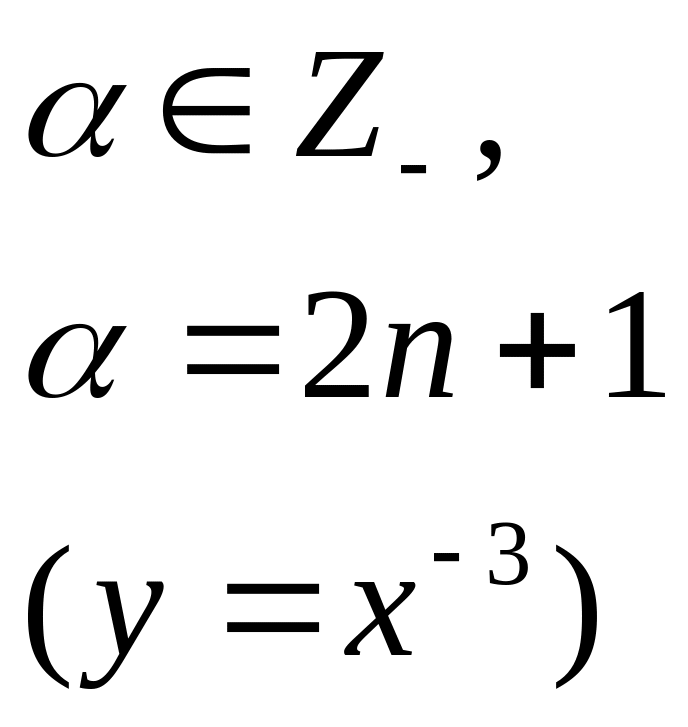- •Алгебра и начала анализа Тема 1 Тригонометрические функции Проверочный тест
- •Ответы:
- •Улучшите свои знания
- •Наиболее часто встречающиеся ошибки
- •Контрольный тест
- •Найдите:
- •Тема 2: Основные тригонометрические тождества Проверочный тест:
- •Найдите:
- •Ответы:
- •Улучшите свои знания
- •1.Тригонометрические функции одного и того же аргумента
- •2.Формулы сложения тригонометрических функций
- •Формулы приведения
- •4.A) Формулы двойного аргумента
- •Тангенс двойного аргумента:
- •1.Синус половинного аргумента: six
- •2.Косинус половинного аргумента: cos
- •3.Тангенс половинного аргумента:tg X
- •Наиболее часто встречающиеся ошибки
- •Контрольный тест
- •2.Простейшие тригонометрические уравнения
- •3.Виды тригонометрических уравнений:
- •2.Однородные тригонометрические уравнения.
- •5.Некоторые другие виды тригонометрических уравнений
- •6.Уравнения, решаемые с помощью применения свойств ограниченности тригонометрических функций
- •Наиболее часто встречающиеся ошибки
- •Контрольный тест
- •Свойства обратных тригонометрических функций в таблицах(5)
- •Ответы:
- •Улучшите свои знания
- •1. Применение производной к определению промежутков монотонности
- •Решить неравенсва
- •4.Записать ответ:
- •2.Применение производной для отыскания точек экстремума
- •Используя результаты исследования, построить график.
- •5. Применение производной для нахождения наибольшего и
- •5.Выбрать из этих значений наибольшее и наименьшее.
- •6.Применение производной для определения мгновенной скорости.
- •7.Применение производной к решению геометрических задач
- •8.Уравнение касательной к графику функции f(X) в точке (x0 ; f(x0))
- •1.Записать уравнение касательной к графику функции в точке f(X) в точке (x0 ; f(x0)):
- •4.Подставить найденные значения в уравнение пункта 1.
- •Наиболее часто встречающиеся ошибки
- •1.Арифметическим корнем n- ой степени из числа a называется неотрицательное число, n- ая степень которого равна a.
- •2.Корнем n- ой степени из числа a называется число, n- ая степень которого равна a.
- •3.Свойства корней n- ой степни
- •Основные тождества
- •Наиболее часто встречающиеся ошибки
- •Контрольный тест
- •Тема 8 Степень с рациональным показателем Проверочный тест:
- •Улучшите свои знания
- •Степенью положительного числа a с рациональным показателем , m – целое, n – натуральное называется корень n- ой степени из числа a в степени m n, т.Е. .
- •2.Вычислить значение степени с рациональным показателем можно, если степень с рациональным показателем заменить корнем.
- •3.Свойства степени с рациональным показателем и положительными основаниями :
- •4.Разложение на множители
- •Контрольный тест
- •Тема 9 Показательная функция Проверочный тест:
- •Улучшите свои знания
- •6.Показательные уравнения
- •7.Показательные неравенства
- •Контрольный тест
- •Тема10 Свойства логарифмов и логарифмическая функция Проверочный тест:
- •Улучшите свои знания
- •2. Основное логарифмическое тождество:
- •3. Свойства логарифмов
- •Контрольный тест
- •Дополнительные материалы
Тема 8 Степень с рациональным показателем Проверочный тест:
1. Представьте степень с рациональным показателем в виде корня:
а)
![]() ;
б)5
;
б)5![]() ;
в)
;
в)
![]() ; г)
; г)
![]() ;
;
2.Вычислите :
![]() ;
;
3.Найдите значение выражения
а)
![]()
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
;
4.Разложите на множители:
а)
![]() -
-
![]() б)
a-b;
( a,
b
– положительные числа); в)
б)
a-b;
( a,
b
– положительные числа); в)
![]() ,(
a,
b
– положительные числа).
,(
a,
b
– положительные числа).
5.Сократите дробь
 .
.
Ответы:
1.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;г
)
;г
)![]() ;
;
2.а)0,95. 3.а) 6; б)4;в)![]() ; г) 10; д)24,5. 4.а)
; г) 10; д)24,5. 4.а)![]() ;
б)
;
б)![]()
в)![]() ;
5.
;
5.
![]() .
.
Улучшите свои знания
Степенью положительного числа a с рациональным показателем , m – целое, n – натуральное называется корень n- ой степени из числа a в степени m n, т.Е. .
Например,
![]() =
=![]() ;
6
;
6![]() .
.
2.Вычислить значение степени с рациональным показателем можно, если степень с рациональным показателем заменить корнем.
Например,
![]() ;
;
![]() .
.
3.Свойства степени с рациональным показателем и положительными основаниями :
а) при умножении степеней с одинаковыми основаниями показатели
складываются, т.е.
![]() .
.
б) при делении степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель степени делителя, т.е.
![]() .
.
Например,
![]() .
.
в) при возведении степени в степень основание остается прежним, а
показатели перемножаются
, т.е.
![]() .
.
Например,
![]() .
.
г) при возведении в степень произведения в эту степень возводится каждый сомножитель, а результаты перемножаются, т.е.
![]() .
.
Например,
![]() .
.
д) при возведении в степень частного, в эту степень возводится, делимое и делитель и результаты делятся, т.е.
 .
.
Например,
![]() .
.
4.Разложение на множители
При разложении на множители выражений с рациональными показателями используются те же методы, что и для многочленов:
а) Вынесение общего множителя за скобки ( за скобки выносится множитель с наименьшим показателем)
Например, разложите на
множители:
![]() .
.
![]() .
.
б) Применение формул сокращенного умножения.
Например, разложите на множители a-b(а и b положительные числа).
a-b
=![]()
в) Применение способа группировки.
Например, разложите на
множители:
![]()
![]()
г) Упрощение выражений с рациональными показателями.
При упрощении выражений, содержащих рациональные показатели
выполняются общие правила и алгоритмы для упрощения дробно – рациональных выражений.
Например, сократите дробь:
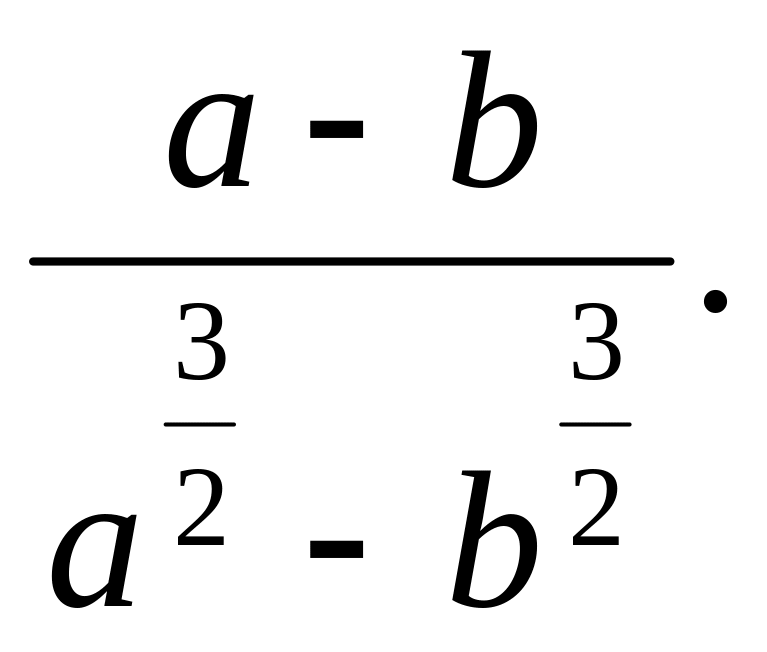

Наиболее часто встречающиеся ошибки:
!Проверь, не делаешь ли ты так!
1.![]() ,
правильно будет:
,
правильно будет:
![]() .
.
2.![]() ,
правильно будет:
,
правильно будет:
![]()
3.
![]() ,
правильно будет:
,
правильно будет:
![]()
4.
![]() ,
правильно будет
,
правильно будет
![]() .
.
Контрольный тест
1.Найдите значение выражения:
![]() .
.
2.Вычислите:
![]() .
.
3.Выполните указанные действия:
![]() .
.
Свойства степени с рациональным показателем в таблицах(16)
№ |
Свойства |
Применение |
Примечания |
Пример |
1 |
, |
При выполнении перобразований, решении уравнений и неравенств |
Если
|
|
2 |
,
|
При выполнении перобразований, решении уравнений и неравенств. |
Применятся и справа налево:
. |
|
3 |
,
|
При выполнении перобразований, решении уравнений и неравенств. |
Применятся и справа налево:
|
|
4 |
|
При выполнении перобразований, решении уравнений и неравенств. |
Применятся и справа налево:
|
|
5 |
,
|
При выполнении перобразований, решении уравнений и неравенств. |
Применятся и справа налево:
|
|
6 |
,b>0 |
При выполнении перобразований, решении уравнений и неравенств |
Применятся и справа налево:
|
|
Тестовые задания: свойства степени с дробным показателем (17)
1 |
Результат упрощения выражения
|
1). a0,5 ; 2) a - 0,5 ; 3) - a0,5 ; 4) -a - 0,5 ; 5) - a. |
5 |
2 |
Результат упрощения выражения:
|
1).a-b; 2) 3)-( 5)
|
3 |
3 |
Если 4x + 4-x =3, то 64x + 64-x равно |
1)27;2)18;3)9;4)24; 5) 36. |
2 |
4 |
Результат упрощения выражения
|
1) 3) - x0,5 ; 4)1; 5) - |
5 |
5 |
Результат упрощения выражения
|
1)x-1; 2) 3) x+ x0,5 +1; 4)1; 5) x+ 1. |
1 |
6 |
Результат упрощения выражения:
равен |
1).a-b; 2) 3) ; 4)1; 5) 2. |
4 |
7 |
Равенство
|
1.
2)
3)
4)
5).
|
2 |
8 |
Результат упрощения выражения
|
1).3 5 y2 ; 2)0; 3)1/9; 4)y -4; 5) y 2 . |
5 |
9 |
Результат упрощения выражения
|
1).a-0,5; 2) a+0,5; 3) 5) 2. |
4 |
10. |
Вычислите
|
1)7;2)4;3)5;4)9; 5)10. |
1 |
11 |
Число, обратное значению выражения
|
1)64/625;2)4/27;3)125/64;4)1/3; 5)16/125. |
3 |
12 |
Результат упрощения выражения
|
1).a -3; 2) a +3; 3) 5) 2. |
3 |
13 |
Результат упрощения выражения
|
1). a0,5 ; 2) a - 0,5 ; 3) - a0,5 ; 4) -a - 0,5 ; 5) - a. |
1 |
14 |
Результат упрощения выражения
|
1). 4a0,5 ; 2)4a - 0,5 ; 3) - 4a0,5 ; 4) -a - 0,5 ; 5) 4a. |
5 |
15 |
Если 5 x -5 –x = 2, то значение выражения 125 x -125 – x равно |
1)17;2)4;3)10;4)9; 5)14. |
5 |
16 |
Упростите выражение и
вычислите его значение при a=2,03
|
1)7;2)0,4;3)0;4)0,9; 5)1. |
5 |
17 |
Найдите значение выражения
|
1)0;2)5;3)0,5;4)1; 5)0,1. |
2 |
18 |
Упростите выражение и
вычислите его значение при x=1/11;
y=3
|
1)0;2)4;3)0,5;4)1; 5)0,1. |
5 |
19 |
Упростите выражение и
вычислите его значение при a= |
1)0;2)4;3)0,5;4)-0,5; 5)0,1. |
4 |
20 |
Упростите выражение
|
1). xy0,5 ; 2)xy - 0,5 ; 3) – xy0,5 ; 4) x1/3 y; 5) xy 1/3. |
4 |
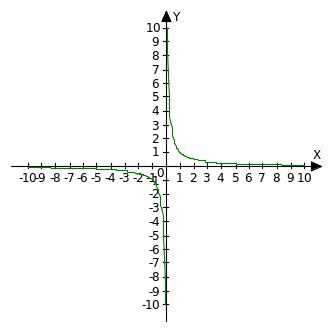
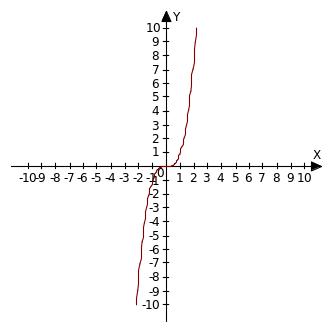
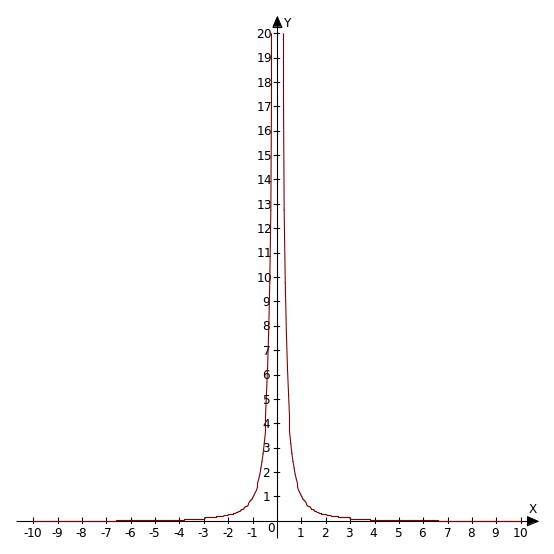
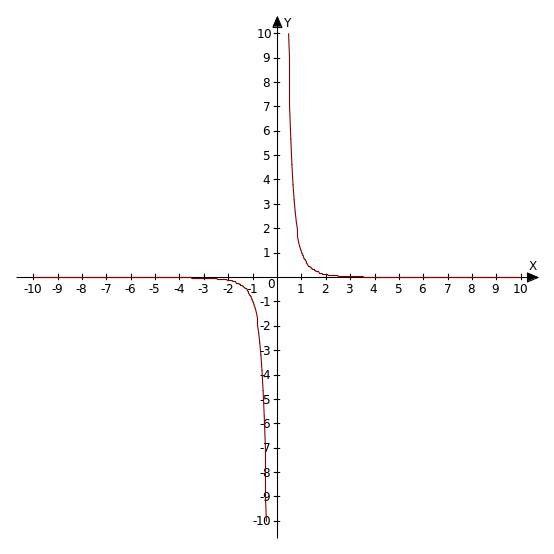
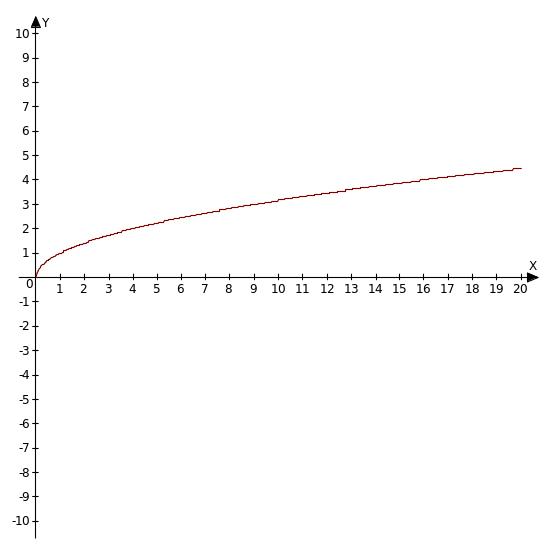
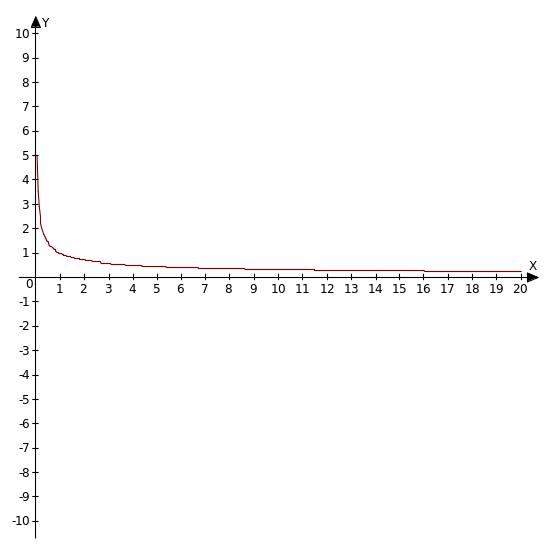
Свойства функции y =
![]() в таблице (18)
в таблице (18)
|
|
|
|
|
|
|
|
Область определения (D) |
|
|
|
|
|
|
|
Множество значений (E) |
|
|
|
|
|
|
|
Четность или нечетность функции |
Нечетная |
Четная |
Нечетная |
Четная |
Нечетная |
Не является четной, не является нечетной |
Не является четной, не является нечетной |
Знаки функции |
y>0, если
|
y≥0 на D |
y>0, если |
y≥0 на D |
y>0, если |
y≥0 на D |
y≥0 на D |
Нули функции |
- |
x=0 |
x=0 |
- |
- |
x=0 |
- |
Промежутки возрастания |
- |
|
|
|
|
|
- |
Промежутки убывания |
|
|
|
|
|
|
|
Наибольшее значение |
- |
- |
- |
- |
- |
- |
- |
Наименьшее значение |
- |
0 |
- |
- |
- |
0 |
- |
Графики |
|
|
|
|
|
|
|
Тестовые задания в таблицах: свойства степенной функции(19)
№ |
Задание |
Ответ |
1 |
Решите уравнение
|
1)4/5;2)
3)16; -16;4) 32; 5) |
2 |
Решите уравнение
|
1)4/5;2) ; - ; 3)16; -16;4) 32; 5) |
3 |
Решите уравнение
|
1)4/3;2) ; - ; 3)8;
-8;4)
|
4 |
Решите уравнение
|
1)-4/3;2) ; - ; 3)
|
5 |
Найдите область определения функции
|
1) (- ∞; 1]; 2) (1; 3); 3) [3; + ∞); 4) [1; 3]; 5) (- ∞; 1).
|
6 |
Найдите область определения функции
|
1) (- ∞; 1]; 2) (-∞;3); 3) (1; 3); 4) [1; 3]; 5) (- ∞; 1)
|
7 |
Возрастающей на множестве всех положительных чисел является функция: |
* |
8. |
Убывающей на множестве всех положительных чисел является функция: |
* |
9. |
Найдите область определения функции
|
1) (- ∞; 1]; 2) (1; 3); 3) [3; + ∞); 4) [1; 3]; 5)
(- ∞; 1)
|
10 |
Найдите область определения функции
|
1) (- ∞; 1]; 2) (-∞;3); 3) (1; 3); 4) [1; 3]; 5) (1;3)
|
11 |
Четной является функция: |
|
12 |
Нечетной является функция: |
|

 .
.
 равен
равен
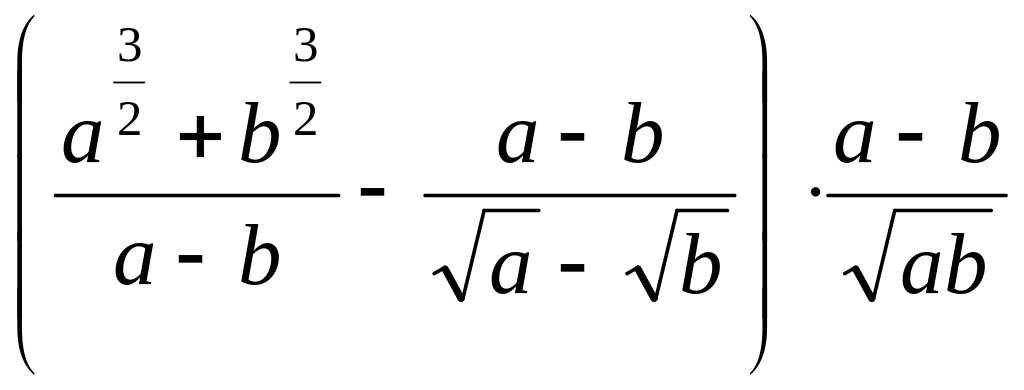 равен
равен
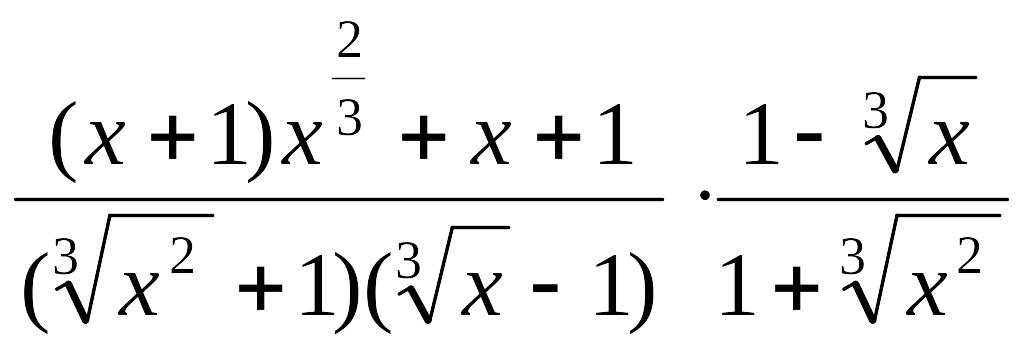 равен
равен

 равен
равен
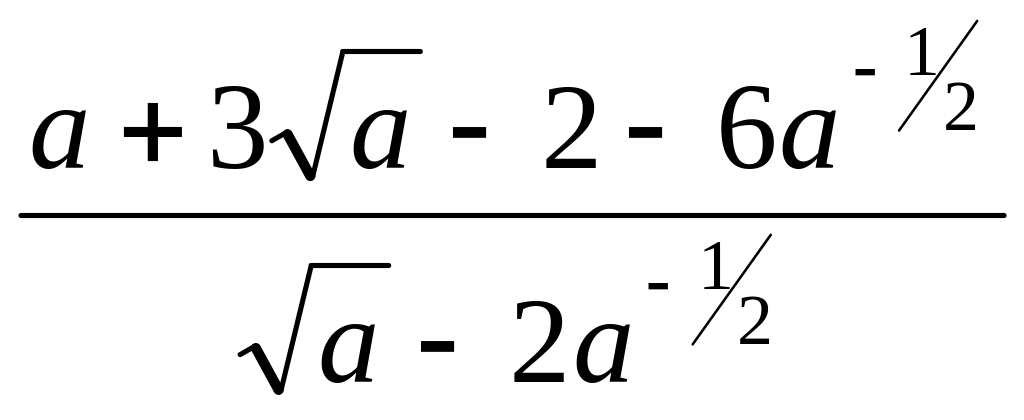 равен
равен
 равен
равен