1. Используя результаты исследования, построить график.

На первом рисунке отметили точки пересечения графика функции с осями координат ( пункты исследования 4 и 5).

На втором рисунке отметили экстремумы (пункт исследования 6).

На третьем – достроили график на промежутках возрастания и убывания функции (пункт исследования 6) .

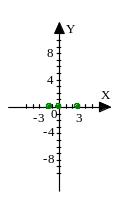
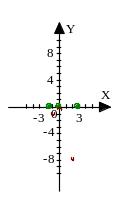
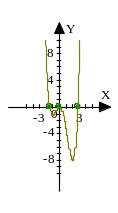
5. Применение производной для нахождения наибольшего и

наименьшего значений функции.

Чтобы найти наибольшее и наименьшее значение функции f(x) на отрезке [a;b], ( например, f(x) = -2x³ - 6x² +5 на [ -1;1] ) надо:.

1.Найти производную функции;( f'(x) = -6x² -12x)

2. Найти точки, в которых производная равна нулю или не существует ( критические точки функции); ( f'(x) = 0;

-6x² -12x=0, -6x(x+2)=0, x =0, x=-2)

3.Выбрать из этих точек те, которые принадлежит промежутку [a;b];( только точка x =0 принадлежит промежутку

[ -1;1] )

4.Вычислить значения функции в выбранных критических точках и на концах промежутка [a;b];( f(0) =5; f(-1) =1;

f(1) =-3.)

5.Выбрать из этих значений наибольшее и наименьшее.

Наибольшее значение функции f(x) = -2x³ -6x² +5 на [ -1;1] равно 5;

наименьше значение функции f(x) = -2x³ -6x² +5 на [ -1;1] равно-3.

6.Применение производной для определения мгновенной скорости.

Если движение точки задано уравнением s(t), то в момент времети t_o

скорость ее движения равна s'(t).

Например, прямолинейное движение точки задано уравнением

s(t) = 2t² -8t -10м. Найдите скорость движения в момент времени t =3c.

Решение.

1.Вычислим s' (t)= (2t² -8t -10)' = 4t -8.

2.Найдем значение s' (2), s' (3)= 4∙3-8 =4(м/c )– это скорость движения в момент времени 3с.

7.Применение производной к решению геометрических задач

Чтобы найти тангенс угла наклона касательной, к оси абсцисс проведенной к графику функции f(x) в точке (x₀ ; f(x₀), нужно

1.Найти производную функции ( f'(x) );

2.Найти значение производной в точке x₀ ( f'(x₀) );

3. Полученное значение будет равно тангенсу угла наклона, т.е. tgα = f'(x₀).

Например: Найдите угол наклона к оси абсцисс касательной, проведенной к графику функции у = x² в точке с абсциссой x₀ = 0,5.

1. Найдем производную функции f(x) = x², f^''(x) = 2x.

2. Найдем значение производной в точке x₀ = 0,5, f^''(0,5) = 1.

3. Тангенс угла наклона касательной к оси абсцисс равен 1.

Можно определить угол наклона касательной к оси абсцисс:

он равен 45˚, т.к. tg45˚ = 1.

8.Уравнение касательной к графику функции f(X) в точке (x0 ; f(x0))

Чтобы составить уравнение касательной к графику функции f(x) в точке (x₀ ; f(x₀)), надо

1.Записать уравнение касательной к графику функции в точке f(X) в точке (x0 ; f(x0)):

у =f'(x₀)x- f'(x₀)x₀ + f(x₀);

2. Найти значение производной в точке x₀( f'(x₀) );

3. Найти значение функции в точке x₀( f(x₀) );

4.Подставить найденные значения в уравнение пункта 1.

Например:

Составьте уравнение касательной, проведенной к графику функции

y = x³+1 в точке ( 1; 2).

1. Запишем уравнение касательной:

у =f'(x₀)x- f'(x₀)x₀ + f(x₀);

2.Найдем значение производной в точке x₀ =1:

f'(x) = 3x², f'(1)=3;

3.Найдем значение функции в точеке x₀ =1: f(1) =2;

4. Подставим найденные значения в уравнение:

у =3x - 3∙1 + 2;

у =3x – 1- это уравнение касательной, проведенной к графику функции

y = x³+1 в точке ( 1; 2).