О.Н.Пирютко

Справочник- тренажер для подготовки к ЦТ

Алгебра. 10-11 классы

Предисловие

Книга написана для тех, кто самостоятельно хочет повторить школьную математику за 10-й - 11-й классы и подготовиться к ЦТ.

В книге изложено 10 тем, которые содержат весь программный курс математики 10-11 классов школы. Для повторения курса по каждой из тем попробуйте сначала написать тест, он называется “проверочным”, затем проверьте ответы. Если вы не можете выполнить задание или сделали в нём ошибку, в следующем разделе (“Улучшите свои знания”) под тем же номером, что и задание, вы найдёте правило и (самое главное!) алгоритм или схему его применения с подробными примерами. Вам станет ясно, в чём же была проблема. Далее проверьте себя по разделу “Наиболее часто встречающиеся ошибки”. Для использования полученной информации при решении итестовых заданий помогут предложенные таблицы и схемы, в которых коротко изложены необходимые для выполнения заданий тестирования материалы.

Эта книга также будет полезна учителям и учащимся 10-11 классов как справочник - помощник, т.к. содержит таблицы основных формул и методов решения заданий каждого раздела с указания к их применению. В конце каждого раздела приводятся тестовые задания для контроля степени подготовленности к Ц.Т.

Автор.

Алгебра и начала анализа Тема 1 Тригонометрические функции Проверочный тест

1. Найдите:

а) область определения функций,

б) множество значений функций:

y = -3sinx; y = tgx+5; y = cos2x.

2. Определите период функций:

а) y = sin2x; б)y = cos 0,5x; в)y = tg7x.

3. Выясните, какие из функций являются четными, какие – нечетными, а какие – ни четными, ни нечетными:

а) y= tg2x; б)y = sinx∙cos 3x; в)y= ⅓cosx; г)y = sinx + cosx.

4. Определите знак произведения:

а) sin50° · cos60° · sin 188° · cos 189°;

б) tg2 · cos5.

5. Что больше: а)sin 37° или sin 67°; б)cos 54° или cos45°; в)tg59° или tg13°?

6. Постройте графики функций:

а)y = sin2x; б) y = cos х/2; б)y = tg ¼x.

Ответы:

1. а) х – любое число; х ≠ π/2 +πk , k – целое число; х – любое число.

б) [-3; 3]; (-∞; +∞); [-1; 1] .

2. а)π; б)4π; в)π/7.

3. в) четная функция; а) б) – нечетные функции, г) не является ни четной функцией, ни нечетной.

4. а) “плюс”; б) “минус”.

5. а) sin 67° > sin 37°; б)cos45° >cos 54°;в) tg59° >tg13°.

Улучшите свои знания

1. a)Область определения(D) тригонометрических функций:

D (sin x) = (-∞; +∞);

D (cosx) = (- ∞; +∞);

D (tgx): х ≠ π/2 +πk , k – целое число.

Примеры

Найдите область определения функций:

1.y = 2sin5x; 2.y = -cos4x; 3. y= tg3x.

Решение

1.Так как область определения функции y = sint – все действительные числа,

т. е. t (-∞; +∞),то 5x тоже принадлежит этому промежутку, 5x (-∞; +∞), значит, х (-∞; +∞). D(2sin5x) = (-∞; +∞).

2.Так как область определения функции y = cost – все действительные числа, т. е. t (-∞; +∞),то 4x тоже принадлежит этому промежутку,

4x (-∞;+∞), значит, х (-∞; +∞). D(-cos4x) = (- ∞; +∞).

3.Так как область определения функции y = tgt все действительные числа, кроме t = π/2 +πk, где k – целое число, то 3х ≠ π/2 + πk , k – целое число, т.е.

х ≠ π/6+πk/3, k – целое число. D (tg3x): х ≠ π/6 +πk/3, k – целое число.

b) Множество значений (E) тригонометрических функций:

E (sinx) = [-1; 1];

E (cosx) = [-1; 1];

E (tgx) = (-∞; +∞).

Примеры

Найдите множество значений функций:

1. y = 2sin5x; 2. y = -cos4x; 3. y = tg3x.

Решение

1. Так как множество значений функции sint – отрезок [-1; 1], то

-1 ≤ sin5x ≤1, т.е. -2≤2 sin5x ≤2, значит, Е(2sin5x) = [-2;2].

2. Так как множество значений функции cost – отрезок [-1; 1], то

-1 ≤сos4x ≤1, т.е. -1 ≤ -сos4x ≤1, значит, Е (-cos4x) =[-1;1].

3. Так как множество значений функции tg t - вся числовая прямая:

(-∞;+∞), то Е (tg 3x) = (-∞; +∞).

2. Функция f(x) называется периодической с периодом Т >0, если для любого х из области определения функции (х ± Т) тоже принадлежит области определения функции, и f(х ± Т) = f(x).

Свойства:

1. Если Т – период функции f(x), то число kT – тоже период f(x), где k – произвольное целое число.

2. Если Т – период функции f(x), то период функции f(mx) (m – некоторое действительное число, не равное нулю) равен Т/m.

Наименьший период функций y =sinx и y =cosx равен 2π, функции y=tgx равен π.

Примеры

Определите период функции: 1.y=sin2x; 2.y= tg7x.

Решение

1. Так как период функции y = sinx равен 2π, то период функции y= sin2x равен 2π/2=π.

2. Так как период функции tgx равен π, то период функции y=tg7x равен π/7.

3. Функция f(x) называется четной, если для любого x из области определения функции f(x) -x также принадлежит области определения и

f(-x) = f(x).

Функция f(x) называется нечетной, если для любого x из области

определения функции f(x), - x также принадлежит области определения и

f(-x) = - f(x).

Примеры

Установите четность или нечетность функции:

1. y= x²-|x|; 2.y =x³ - x; 3. y = 3√x+5; 4.y = x - x².

Решение

1. Область определения данной функции – все действительные числа,

f(-x)= (-x)²-|-x| = x²- |x| = f(x), значит, функция y= x²-|x| четная.

2. Область определения данной функции – все действительные числа,

f(-x) = (-x)³ -(- x) = - x³ + x =-( x³ - x) = - f(x), значит, функция y = x - x²

нечетная.

3. Область определения данной функции – все неотрицательные

действительные числа. Значит, если x D(3√x+5), тo

– x D(3√x+5),т.е.данная функция не является ни четной, ни нечетной.

4. Область определения данной функции – все действительные числа,

f(-x)= -x- (-x)² =-x -x² =-(x+x²) ≠ - f(x) ≠ f(x), значит, данная функция не

является ни четной, ни нечетной.

Функции y= sinx и y=tgx являются нечетными, функция cosx – четная:

sin(-x)=-sinx; tg(-x) = -tgx; cos(-x) =cosx.

Примеры

Выясните, какие из функций являются четными, какие – нечетными, а какие – ни четными, ни нечетными:

1. y = -2 sin 6x + tg4x;

2. y = 4cos 3x + 3;

3. y = sinx + cosx.

Решение

Области определения этих функций симметричны относительно x=0, поэтому поверим только второе условие четности и нечетности.

1. f(-x) =-2sin 6(-x )+tg4(-x) = 2 sin 6x - tg4x= -(-2 sin 6x +tg4x) =- f(x),

функция является нечетной.

2. f(-x) = 4cos 3(-x) + 3 =4cos 3x + 3= f(x), функция является четной.

3. f(-x) = sin(-x) + cos(-x) = -sinx +cosx ≠ - f(x) ≠ f(x), значит, функция не

является ни четной, ни нечетной.

4.Промежутки знакопостоянства и нули функции.

П ромежутки знакопостоянства функции – числовые промежутки, на которых функция сохраняет свой знак (т.е. остается положительной или

отрицательной). y

Промежутки знакопостоянства функции sinx

y= sinx: sinx

sinx > 0 х (2πk; π +2πк), k – любое целое

число;

sinx < 0 х (π +2πк; 2πk), k – любое целое х

число.

П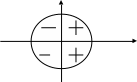 ромежутки знакопостоянства функции

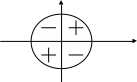
y = cosx: y

cosx > 0 х (-π/2 +2πk; π/2 +2πк), k – любое cosx

целое число;

cosx < 0 х (π/2 +2πк; 3π/2+2πk), k – любое

целое число. х

y

Промежутки знакопостоянства функции tgx

y=tgx: tgx

tgx > 0

х (πk; π/2 +πк), k – любое целое число;

tgx <0 x

х (-π/2 +πк; πk), k – любое целое число.

Нулями функции называются значения аргумента, при которых значение функции равно нулю.

Нули функции sinx: sinx=0, x= πк, k – любое целое число.

Нули функции cosx: cosx= 0, x = π/2 +πк, k – любое целое число.

Нули функции tgx: tgx =0, x= πк, k – любое целое число.

Примеры

Определить знак произведения:

1. sin57° · cos80° · sin 108° · cos 139° ;

2.tg67°∙sin73° ∙cos 246°;

3. tg4 · sin2· cos1.

Решение

1. Так как угол 57° принадлежит первой четверти (т.е. 0° <57°< 90°), то sin57° > 0. Угол 80° также принадледит первой четверти, значит, cos80°>0. Углы 108° и 139° принадлежат второй четверти четверти (т.е. 90° <108°< 180°, 90° <139°<180°, ),, то

sin 108° >0, cos 139° <0. Значит, sin57° · cos80° · sin 108° · cos 139° <0,

как произведение трех положительных и одного отрицательного чисел.

2. Углы 67° и 73° принадлежат первой четверти, угол 246° - третьей, значит, tg67°>0, sin73° >0, cos 246°<0, т.е. tg67°∙sin73° ∙cos 246° <0.

3. Так как π ≈ 3.14, то π < 4 < 3π/2, то угол 4 радиана принадлежит третьей четверти, т.е. tg4 > 0. Аналогично, угол 2 радиана принадлежит второй четверти, т.е. sin 2 > 0, и угол 1радиан принадлежит первой четверти, cos1>0. Значит, tg4 · sin2· cos1 >0.

5. Функция f(x) называется возрастающей на множестве М, если для любых двух значений аргумента из множества М (х₁ и x₂), большему значению аргумента соответствует большее значение функции (если х₁>x₂, то

f(x₁)>f(x₂), а если х₁<x₂, то f(x₁)<f(x₂)).

Функция f(x) называется убывающей на множестве М, если для любых

двух значений аргумента из множества М (х₁ и x₂), большему значению аргумента соответствует меньшее значение функции (если х₁>x₂, то

f(x₁) <f(x₂), а если х₁<x₂, то f(x₁) >f(x₂)).

Функция, только возрастающая или только убывающая на множестве М, называется монотонной на этом множестве.

Функция y=sinx возрастает на промежутках (- π/2 +2πк; π/2+2πk), k – любое целое число.

Функция y=cosx возрастает на промежутках (- π+2πк; 2πk), k – любое целое число.

Функция y=sinx убывает на промежутках (π/2 +2πк; 3π/2+2πk), k – любое целое число.

Функция y=cosx убывает на промежутках (2πк; π+2πk), k – любое целое число.

Функция y =tgx возрастает на промежутках (- π/2 +πк; π/2+πk), k – любое целое число.

Примеры

Что больше:

1. sin 37° или sin 67°; 2. cos 54° или cos45°; 3. tg59° или tg13°?

Решение

1. Так как функция y= sinx возрастает на промежутке [-90°; 90°],

и 37° [-90°; 90°], 67° [-90°; 90°], и 37° < 67°, то sin 37° < sin 67°.

2. Так как функция y=cosx убывает на промежутке [0°; 180°],

и 54° (0°; 180°), 45° (0°; 180°), и 54° > 45°, то cos 54° < cos 45°.

3. Так как функция y=tgx возрастает на промежутке (-90°; 90°), то

tg 59° > tg13°.

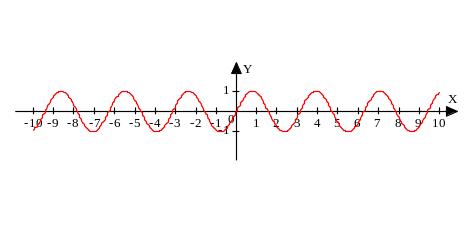
6. График функции y=sinx (рис.4):

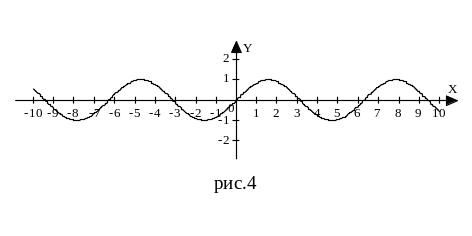
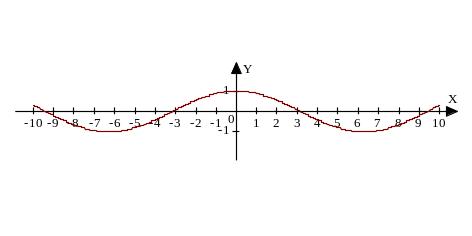
График функции y=cosx (рис.5):

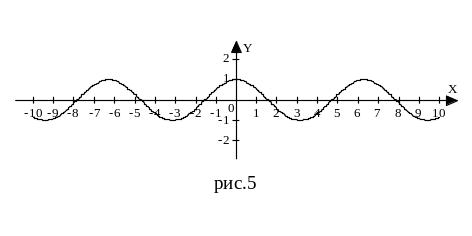
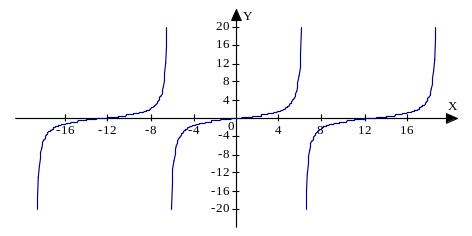
График функции y=tgx (рис.6):

Примеры

1. Построим график функции y=sin2x. Период этой функции равен 2π/2=π. Построим синусоиду на этом периоде (рис.7).

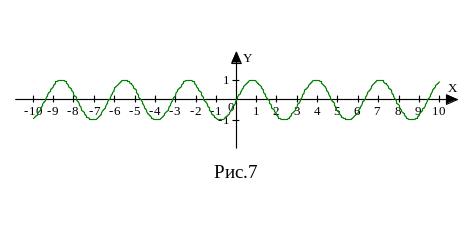
2. Построим график функции y=cos ⅔x. Период cos ⅔x равен 3π. Построим график на этом периоде (рис.8).

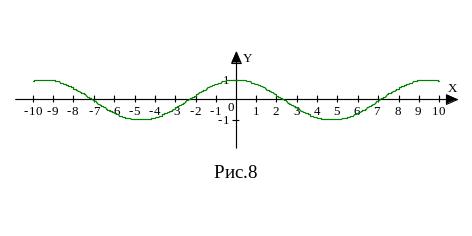
3. Построим график функции y=tg7x. Период tg7x равен π/7. Построим график на этом периоде (рис.9).