181) Вопрос:
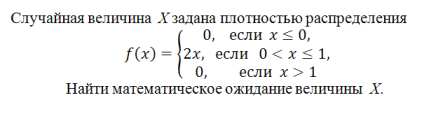
Ответ:
182) Вопрос: В ящике 6 белых и 8 чёрных шаров. Из ящика вынули два шара. Найти вероятность того, что оба шара белые. Ответ: 15/91
183) Вопрос: Три стрелка стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго – 0,8, для третьего – 0,9. Найти вероятность того, что все три стрелка одновременно попадут в цель. Ответ: 0,54
184) Вопрос: Три стрелка стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго – 0,8, для третьего – 0,9. Найти вероятность того, что в цель попадает хотя бы один стрелок. Ответ: 0,995
185) Вопрос: Вероятность попадания в цель первым стрелком равна р1 , а вторым стрелком – р2. Стрелки выстрелили одновременно. Какова вероятность того, что один из них попадает в цель, а другой не попадает? Ответ: р1 + р2 - 2 р2 р1
186) Вопрос: В первом ящике 6 шаров: 1 белый, 2 красных и 3 синих. Во втором ящике 12 шаров: 2 белых, 6 красных, 4 синих. Из каждого ящика вынули по шару. Какова вероятность, что среди вынутых шаров нет синих? Ответ: 1/3
187) Вопрос: В классе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из двух человек. Какова вероятность, что выбраны два мальчика? Ответ: 22/145
188) Вопрос: В классе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из двух человек. Какова вероятность, что выбраны две девочки? Ответ: 51/145
189) Вопрос: В классе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из двух человек. Какова вероятность, что выбраны девочка и мальчик? Ответ: 72/145
190) Вопрос: Производится три выстрела по одной мишени. Вероятность попадания при каждом выстреле равна 0,5. Найти вероятность того, что в результате этих выстрелов будет только одно попадание. Ответ: 0,375
191) Вопрос: Имеются три одинаковых по виду ящика. В первом ящике 20 белых шаров, во втором – 10 белых и 10 чёрных шаров, в третьем – 20 чёрных шаров. Из выбранного наугад ящика вынули белый шар. Вычислить вероятность того, что шар вынут из первого ящика. Ответ: 2/3
192) Вопрос:
Ответ:
193) Вопрос:
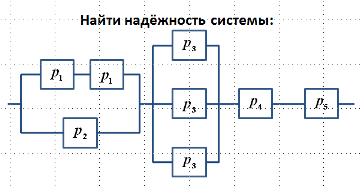
Ответ:
194) Вопрос:
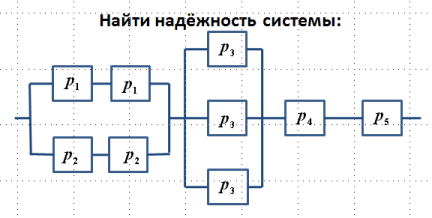
Ответ:
195) Вопрос:
Ответ:
Тема: Задача 3
196) Вопрос:
Ответ:
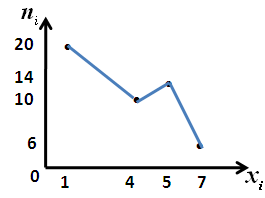
197) Вопрос: В комнате студенческого общежития живут трое студентов. У них есть 4 чашки, 5 блюдец и 6 чайных ложек. Сколькими способами они могут накрыть стол для чаепития (каждый получает одну чашку, одно блюдце и одну ложку) Ответ: 172800
198) Вопрос: На школьном вечере присутствуют 12 девушек и 15 юношей. Сколькими способами можно выбрать из них 4 пары для танца? Ответ: 17417400
199) Вопрос: В селении проживает 2000 жителей. Доказать, что по крайней мере двое из них имеют одинаковые инициалы. Ответ: 841
200) Вопрос: Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки, если известно, что никто из них не получил неудовлетворительной отметки? Ответ: 81
201) Вопрос: В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нём 12 открыток? Ответ: 293930
202) Вопрос: Автомобильные номера состоят из одной, двух или трёх букв и четырёх цифр. Найти число таких номеров, если используются 32 буквы русского алфавита. Ответ: 338200000
203) Вопрос: Сколькими способами можно выбрать 12 человек из 17, если данные двое человек из этих 17 не могут быть выбраны вместе? Ответ: 3185
204) Вопрос: Сколькими способами можно посадить за круглый стол 5 мужчин и 5 женщин так, чтобы никакие два лица одного пола не сидели рядом? Ответ: 28800
205) Вопрос: Пять девушек и трое юношей играют в городки. Сколькими способами они могут разбиться на две команды по 4 человека в каждой команде, если в каждой команде должно быть хотя бы по одному юноше? Ответ: 30
206) Вопрос: На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом 1-ый и 2-ой тома не стояли рядом? Ответ: 28•29!