67) Вопрос:

Ответ:

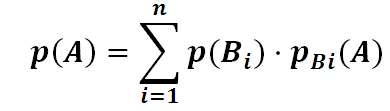
68) Вопрос: Формула Бейеса имеет вид: Ответ:

69) Вопрос: Формула Бернулли имеет вид: Ответ:

70) Вопрос: Формула Пуассона имеет вид: Ответ:

71) Вопрос: Образуют ли полную группу при бросании монеты группы событий: А – появление герба; В – появление цифры? Ответ: да

72) Вопрос: Образуют ли полную группу при бросании двух монет группы событий: А – появление двух гербов; В – появление двух цифр? Ответ: нет

73) Вопрос: Производится два выстрела по мишени. Образуют ли полную группу группы событий: А – ни одного попадания; В – одно попадание; С – два попадания? Ответ: да

74) Вопрос: Производится два выстрела по мишени. Образуют ли полную группу группы событий: А – хотя бы одно попадание; В – хотя бы один промах? Ответ: да

75) Вопрос: Образуют ли полную группу при вынимании карты из колоды группы событий: А – появление карты червонной масти; В – появление карты бубновой масти; С – появление карты трефовой масти? Ответ: нет

76) Вопрос: Являются ли несовместными при бросании монеты группы событий: А – появление герба; В – появление цифры? Ответ: да

77) Вопрос: Являются ли несовместными при бросании двух монет группы событий: А – появление герба на первой монете; В – появление цифры на второй монете? Ответ: нет

78) Вопрос: Производится два выстрела по мишени. Являются ли несовместными группы событий: А - ни одного попадания; В – два попадания; С – одно попадание? Ответ: да

79) Вопрос: Производится два выстрела по мишени. Являются ли несовместными группы событий: А – хотя бы одно попадание; В – хотя бы один промах? Ответ: нет

80) Вопрос: Являются ли несовместными при вынимании двух карт группы событий: А – появление двух чёрных карт; В – появление туза; С – появление дамы? Ответ: нет

81) Вопрос: Опыт состоит в бросании двух монет. Рассматриваются следующие события: A – появление герба на первой монете; B – появление цифры на первой монете; C – появление герба на второй монете; D – появление цифры на второй монете; E – появление хотя бы одного герба; F – появление хотя бы одной цифры; G – появление одного герба и одной цифры; H – непоявление ни одного герба; K – появление двух гербов. Тогда событие A+C равносильно событию: Ответ: E

82) Вопрос: Опыт состоит в бросании двух монет. Рассматриваются следующие события: A – появление герба на первой монете; B – появление цифры на первой монете; C – появление герба на второй монете; D – появление цифры на второй монете; E – появление хотя бы одного герба; F – появление хотя бы одной цифры; G – появление одного герба и одной цифры; H – непоявление ни одного герба; K – появление двух гербов. Тогда событие AC равносильно событию: Ответ: K

83) Вопрос: Опыт состоит в бросании двух монет. Рассматриваются следующие события: A – появление герба на первой монете; B – появление цифры на первой монете; C – появление герба на второй монете; D – появление цифры на второй монете; E – появление хотя бы одного герба; F – появление хотя бы одной цифры; G – появление одного герба и одной цифры; H – непоявление ни одного герба; K – появление двух гербов. Тогда событие EF равносильно событию: Ответ: G

84) Вопрос: В урне a белых и b чёрных шаров. Из урны вынимают один шар. Вероятность того, что этот шар будет белым равна: Ответ:

85) Вопрос: Из урны, в которой a белых и b чёрных шаров, вынимают один за другим все шары, кроме одного. Вероятность того, что последний оставшийся в урне шар будет белым равна: Ответ:

86) Вопрос: Из урны, в которой a белых и b чёрных шаров, вынимают подряд все находящиеся в ней шары. Вероятность того, что вторым по порядку будет вынут белый шар равна: Ответ: