Лекции / Лекции по математике / Математика 1 семестр / 13 Построение гиперболы, парабола

Лекция 13

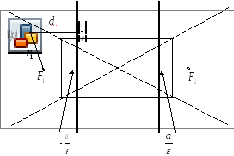
Построение гиперболы

При построении гиперболы необходимо построить прямоугольник со сторонами и и провести диагонали, которые и являются асимптотами (см. рис.). , - вершины гиперболы, - действительная полуось, - мнимая полуось, - центр гиперболы.

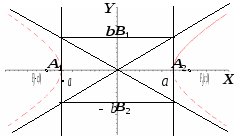
Если , то гипербола называется равносторонней, ее уравнение имеет вид:

(13.1)

.

Уравнение

(13.2)

определяет гиперболу с действительной осью .

Гиперболы, определяемые уравнениями (12.10) и (13.2) называются сопряженными.

Если центр гипербол перенести в точку , то уравнение примет вид: .

Замечание 1.

Уравнение определяет семейство прямых.

Можно выяснить при каких коэффициентах уравнение (12.3) будет определять гиперболу или семейство прямых.

По аналогии с эллипсом - при (*).

Определение 13.1.

Эксцентриситетом гиперболы называется отношение ее фокусного расстояния к расстоянию между вершинами.

Если - действительная ось, то .

Так как для гиперболы , то , , тогда ,

(13.3)

.

Следовательно, эксцентриситет гиперболы характеризует форму прямоугольника и форму самой гиперболы.

(13.4)

,

- формулы фокальных радиусов.

4⁰ Директрисы эллипса и гиперболы.

Определение 13.2.

Директрисами эллипса (гиперболы) называются прямые, перпендикулярные большой оси эллипса (действительной оси гиперболы) и расположенные симметрично относительно центра на расстоянии .

. (13.5)

А) Т.к.

Б) Т.к.

Директрисы эллипса и гиперболы не имеют с кривыми общих точек.

Теорема 13.1.

Отношение расстояния произвольной точки эллипса (гиперболы) до фокуса к расстоянию этой точки до соответствующей директрисы есть постоянная величина, равная эксцентриситету эллипса (гиперболы).

(13.6)

.

Доказательство.

Рассмотрим левый фокус и левую директрису эллипса. Пусть эллипсу, тогда , ; . Если гиперболе (левой ветви), то , ; . Остальные случаи рассматриваются аналогично. ■

5⁰ Парабола.

Определение 13.3.

Параболой называется геометрическое место точек, равноудаленных от прямой, называемой директрисой и точки, называемой фокусом.

Пусть дано: , : , .

Любая точка принадлежит параболе (), т.е. если ; , то

,

(13.7)

-

- каноническое уравнение параболы ().

Здесь - параметр, - вершина параболы, симметрична относительно оси , ветви направлены вправо.

(13.8)

- уравнение директрисы.

Замечание 2.

Если фокус параболы расположен на оси , то уравнение будет иметь вид: (13.9)

Замечание 3.

- уравнение параболы с вершиной в точке .

Замечание 4. Частные случаи:

А) - пара параллельных прямых;

Б) - уравнение не определяет линию;

В) - пара совпадающих прямых.

Выясним, при каких коэффициентах уравнение (12.3) определяет параболу

, , .

Возможно А=0 или С=0 т.е. . Таким образом: :

Пример 13.1

Определить вид кривой и построить ее: .

, . , но т.к. , то ветви направлены влево.

6⁰ Упрощение общего уравнения второй степени.

Пусть кривая второго порядка задана уравнением

.

Перейдем к новым координатам по формулам

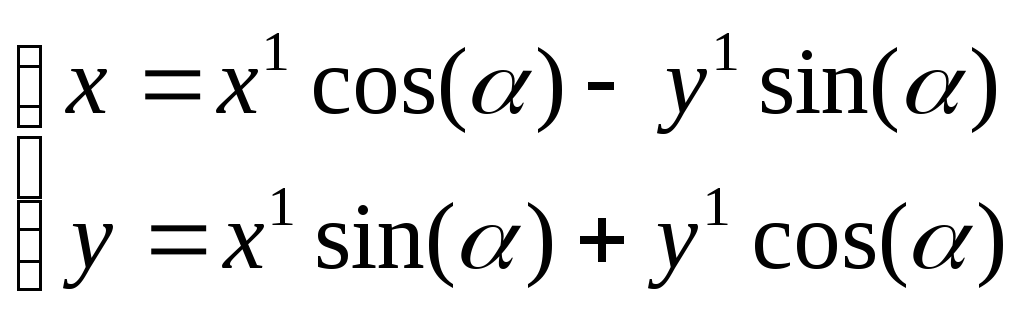, т.е. повернем плоскость на .

, где

,

,

.

Угол поворота выберем так, чтобы , т.е. , или

(13.9)

.

Если , , , .

Утверждение. Коэффициенты и одновременно в нуль не обращаются.

Доказательство.

Пусть вычтем из первого второе, получим:

, , , . Т.о. .

Это возможно только в случае , что противоречит условию .

Пример 13.2.

Определить вид, параметры и расположение линии, заданной уравнением .

, .

По формулам (19) для системы координат .

,

, , - уравнение эллипса. - перешли в систему , , .

6