Лекции / Лекции по математике / Математика 1 семестр / 11 Взаимное расположение, угол, ур. в отрезках, нормаль.

Лекция 11

5⁰ Уравнение прямой в отрезках

Пусть дано общее уравнение прямой:

, , , , тогда

(11.1)

.

- уравнение прямой в отрезках, где - отрезки, которые отсекает прямая на соответствующих осях координат.

Пример11.1.

Построить прямую, заданную общим уравнением . Написать уравнение этой прямой в отрезках.

.

6⁰ Взаимное расположение прямых на плоскости

Утверждение 11. 1.

Для того чтобы прямые и , заданные уравнениями

(*)

совпадали, необходимо и достаточно, чтобы . (11.2)

Доказательство.

и совпадают их направляющие вектора и коллинеарны, т.е.

(11.3)

.

Возьмем точку этим прямым, тогда . Умножая первое уравнение на и прибавляя ко второму в силу (11.2) получим:

(11.4)

.

Итак, формулы (11.2), (11.3) и (11.4) эквивалентны.

Пусть выполняется (11.2), тогда уравнения системы (*) эквивалентны соответствующие прямые совпадают. ■

Утверждение 11. 2.

Прямые и , заданные уравнениями (*) параллельны и не совпадают тогда и только тогда, когда . (11.5)

Доказательство.

Пусть и не совпадают несовместна, т.е. по теореме Кронекера-Капелли . Это возможно лишь при условии , , т.е. при выполнении условия (11.5).

При выполнении первого равенства (11.5); невыполнение второго равенства дает несовместность системы (*) прямые параллельны и не совпадают. ■

Замечание 1. .

Полярная система координат

Зафиксируем на плоскости точку и назовем ее полюсом. Луч , исходящий из полюса, назовем полярной осью. Выберем масштаб для измерения длин отрезков и условимся, что поворот вокруг т. против часовой стрелки будем считать положительным. Рассмотрим любую точку на заданной плоскости, обозначим через ее расстояние до полюса и назовем полярным радиусом. Угол, на который нужно повернуть полярную ось , чтобы она совпала с обозначим через и назовем полярным углом.

Определение 11.3.

Полярными координатами точки называется ее полярный радиус и полярный угол : , , .

Замечание 2. в полюсе. Значение для точек, отличных от точки определено с точностью до слагаемого , .

Рассмотрим декартовую прямоугольную систему координат: полюс совпадает с началом, а полярная ось – с положительной полуосью . Здесь . Тогда:

(11.6)

-

связь между прямоугольной декартовой и полярной системами координат.

Пример 11.2.

- уравнение лемнискаты Бернулли. Записать его в полярной системе координат.

, , , , .

7⁰ Нормальное уравнение прямой на плоскости

Пусть полярная ось совпадает с , - ось, проходящая через начало координат . Пусть , . Пусть , тогда

(*)

Условие (**) для того, чтобы точка .

или

(11.7)

-

уравнение прямой в полярной системе координат.

Здесь - длина , проведенного от начала координат на прямую, - угол наклона нормали к оси .

Уравнение (11.7) можно переписать: , т.к. 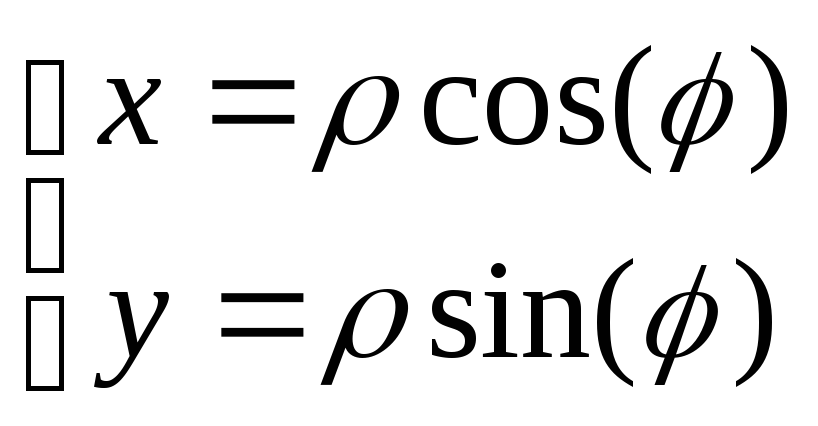, получим

(11.8)

-

нормальное уравнение прямой на плоскости.

Покажем, как общее уравнение прямой привести к нормальному виду: пусть : , тогда нормальное уравнение получается умножением на нормирующий множитель :

.

должны быть координатами единичного вектора. Это значит:

(11.9)

.

Знак выбирается из условия: , т.е. если , .

Нормальное уравнение прямой удобно для нахождения расстояния от произвольной точки до прямой:

(11.10)

.

Пример 11.2.

- общее уравнение. Написать нормальное уравнение.

, .

Умножим обе части исходного уравнения на : . Здесь .

Замечание 3. Формула (11.8) может быть записана в виде:

(11.10’)

.

8⁰ Угол между двумя прямыми

Пусть даны две прямые: . Найти угол между этими прямыми:

.

или

(11.11)

.

5