Лекции / Лекции по математике / Математика 1 семестр / 16 Поверхности...Матанализ. Элементы теории множеств

Лекция 16

6) Двуполостный гиперболоид

Определение 16.1.

Двуполостным гиперболоидом называется поверхность, которая в прямоугольной системе координат определяется уравнением

. (16.1)

С помощью аналогичного исследования нетрудно установить вид поверхности.

В сечениях плоскости oXZ (y=o) и oYZ (x=0) получаются гиперболы

.

При сечениях z=h:

а) при плоскость пересекает поверхность по эллипсу;

б) при плоскости касаются поверхности в точках (0;0;);

в) при точек пересечения плоскости с поверхностью не существует (мнимый эллипс).

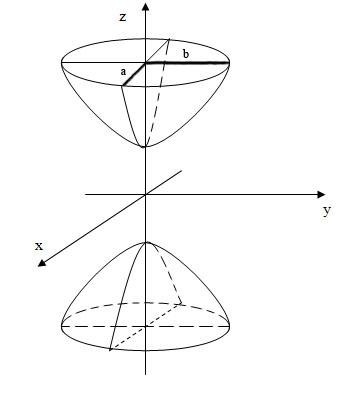
Итак, двуполостный гиперболоид состоит из двух отдельных «полостей», каждая из которых имеет вид бесконечной выпуклой чаши. 7) Эллиптический параболоид

Определение 16.2.

Эллиптическим параболоидом называется поверхность, которая в прямоугольной системе координат определяется уравнением

где - параметры. (16.2)

С помощью сечений исследуем эту поверхность:

1) и 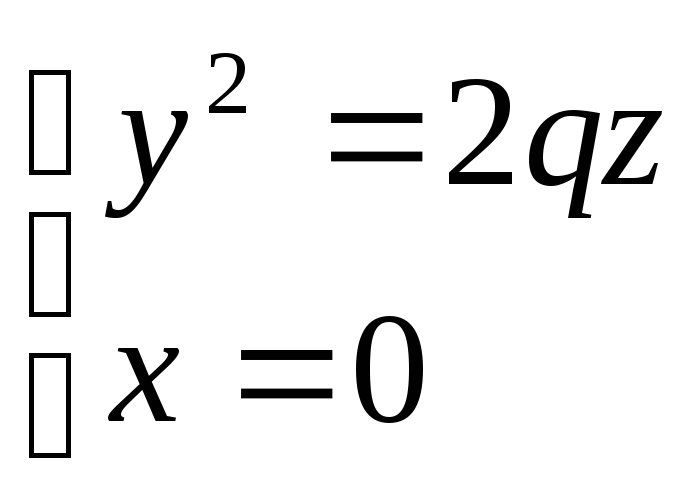(16.3).

(В сечениях параболы: OZ – ось симметрии, O(0;0;0) – вершина)

2)

а) при h>0 сечения – эллипсы;

б) при h=0 плоскость z=0 касается параболоида (эллипс вырождается в точку);

в) при h<0 – мнимый эллипс.

Е

Эллиптический параболоид – бесконечно выпуклая чаша

сли p=q, эллиптический параболоид можно рассматривать, как поверхность, образованную вращением параболы вокруг ее оси (параболоид вращения).

8) Гиперболический параболоид

Определение 16.3.

Гиперболическим параболоидом называется поверхность, которая в прямоугольной системе координат определяется уравнением

(p,q>0). (16.3)

Установим геометрический вид поверхности:

Рассмотрим сечения:

1) . В сечении парабола, OZ – ось симметрии, ветви направлены вверх, вершина – в начале координат.

2). В сечении – такие же (как в (1)) параболы .

3) . В сечении парабола, OZ – ось симметрии, ветви направлены вниз, вершина – в начале координат.

4) . В сечении такие же параболы, как в (3).

5) 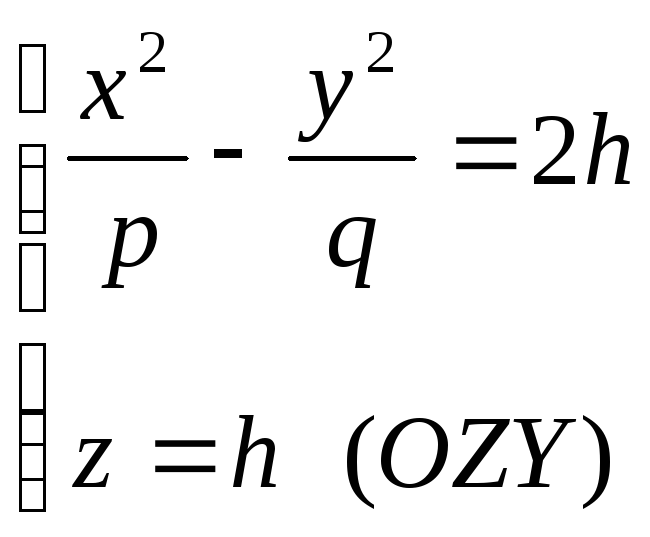или .

а) приh>0 в сечении гиперболы в плоскости OXZ;

б) при h<0 в сечении гиперболы в плоскости OYZ;

в) при h=0 в сечении гипербола вырождается в пару пересекающихся прямых.

Таким образом имеем седлообразную поверхность.

(0;0;0) – вершина, p,q – параметры.

Математический анализ

§1 Элементы теории множеств

16.1. Логические символы

В математике понятия множества первично (не определяется).

Синонимы: совокупность, система, набор, семейство и т.п.

Обозначения: A,B,X,… .

Объекты, из которых состоит множество, называются элементами или точками.

Обозначения: x, y, α, β,… .

Обозначения с помощью логической символики

1) (из того, что следует, что )

2) (α и β эквивалентны, (то есть и )).

Пример 16.1.

Предложение α: два вектора перпендикулярны.

Предложение β: скалярное произведение двух векторов равно нулю.

3)

(для любого элемента x из множества X имеет место предложение α)

– квантор всеобщности.

4)

(существует элемент x из множества X, для которого имеет место предложение)

– квантор существования.

5) – отрицание предложения .

Определение 16.4.

Y подмножество X, если в Y нет элементов, не принадлежащих X или:

(X содержит Y).

Определение 16.5.

X=Y, если множества состоят из одних и тех же элементов:

6) – пустое множество. Не содержит ни одного элемента.

16.2. Операции над множествами

Определение 16.6.

Множество, каждый элемент которого является элементом множества A или B, называется объединением множеств A и B:

(логическое сложение).

Определение 16.7.

Множество, каждый элемент которого является элементом множества A и B, называется пересечением множеств A и B:

(логическое умножение).

Определение 16.8.

Множество, каждый элемент которого является элементом множества A и не является элементом множества B, называется разностью множеств

A и B.

.

Свойства множеств

1⁰ , – коммутативность;

2⁰ а) – ассоциативность;

б)

3⁰ а) ; б)

4⁰ а)

б) – дистрибутивность;

Числовые множества

Числовые множества – множества, объектами которых являются числа.

Пример 16.2.

1) ; 2) ; 3) Q; 4) R;

5) ;

6) .

16.3 Окрестности точки х₀ как особый вид множества

Пусть x₀ ,

тогда - окрестностью х₀ называется интервал:

Число называется радиусом окрестности.

Заметим: ,

где – проколотая окрестность точки x₀

Очевидно,

Введем понятие бесконечно удаленных точек.

Пусть задано сколь угодно большое число M>0.

Определение 16.9.

Окрестностью элемента + называется множество тех точек x, для которых x>M или:

.

Определение 16.10.

Окрестностью элемента - называется множество тех точек x, для которых x<-M или:

.

Определение 16.11.

Окрестностью элемента называется множество тех точек x, для которых |x|>M или:

.

6