Лекции / Лекции по математике / Математика 1 семестр / 2 Действия с матрицами

Лекция 2

2.1. Действия с матрицами

Определение 2.1.

Две матрицы одинакового порядка называются равными, если равны все их соответствующие элементы.

Замечание 1. Две неравные квадратные матрицы одинакового размера могут иметь одинаковые определители.

; .

Определение 2.2.

А) Суммой матриц одинакового размера и называется матрица , полученная поэлементным сложением данных матриц.

Б) Произведением матрицы на число называется матрица , полученная умножением всех элементов матрицы на число .

Замечание 2. Сложение матриц и умножение матрицы на число называются линейными операциями с матрицами.

Замечание 3. В отличие от матриц, в определителе не все его элементы, а элементы только одной строки (столбца) умножаются на число .

Суммы матриц разного порядка не рассматриваются.

Примеры 2.1.

1) , ;

.

2) , ;

.

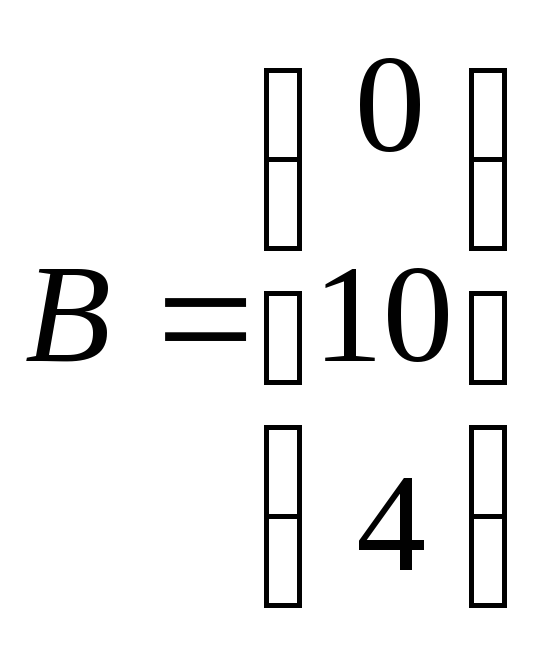2.2. Свойства линейных операций с матрицами

Пусть А, В, С – матрицы одинакового размера, - числа

- переместительное свойство сложения матриц (коммутативность);

- сочетательное свойство сложения матриц (ассоциативность);

- ассоциативность умножения матрицы на число;

- распределительное свойство умножения матрицы на число относительно суммы чисел (дистрибутивность);

- дистрибутивность умножения матрицы на число относительно суммы матриц.

Докажем свойства (3) и (5) (остальные доказываются по аналогии).

Доказательства.

. Пусть и , тогда

.

Здесь использовались: определение 2.2(б), свойство умножения матрицы на число.

. Пусть и . Тогда

Благодаря этим свойствам при выполнении многих операций с матрицами можно обращаться как с обычными числами.

Определение 2.3.

Произведением матрицы на матрицу называется матрица с элементами:

, , (2.1),

( - сумма произведений элементов -ой строки первой матрицы на соответствующие по порядку элементы -го столбца второй матрицы).

Замечание 4:

А) Согласно этому определению, умножать можно только такие две матрицы, когда число столбцов первой матрицы совпадает с числом строк второй. Произведение имеет столько строк, сколько первая матрица, и столько столбцов, сколько вторая.

В противном случае произведение не определено.

Б) Произведение матриц не является линейной операцией.

С) Операция умножения матриц некоммутативна.

Обозначение: .

Примеры 2.2.

1) Пусть

.

2)Пусть , . Показать, что .

2.3. Свойства умножения матриц

Пусть, размеры матриц таковы, что произведения матриц имеют смысл..

1) – ассоциативность умножения;

2) – дистрибутивность умножения матриц относительно суммы матриц;

Определение 2.4.

Квадратная матрица называется единичной матрицей.

Очевидно, что det Е=1.

2.4. Свойство единичной матрицы

, (2.2)

(2.2’)

для матрицы размера (равенство (2.2))

или размера (равенство (2.2’))

и единичной матрицы размера .

Определение 2.5.

Матрица, все элементы которой равны нулю, называется нулевой матрицей.

.

Очевидно, что , .

2.5. Понятие обратной матрицы

Определение 2.6.

Квадратная матрица называется обратной по отношению к матрице , если выполняется равенство , где – единичная матрица.

Определение 2.7.

Квадратная матрица называется невырожденной, или неособенной, если . Если , то матрица называется вырожденной (особенной).

Теорема 2.1.

Всякая невырожденная матрица имеет обратную матрицу, определяемую формулой:

(2.3)

Замечание 5.

В равенстве (2.3) матрица

получена из матрицы

заменой ее элементов на соответствующие алгебраические дополнения и последующим транспонированием. Такая матрица называется присоединенной (союзной) матрицей для матрицы.

Таким образом,

.

Доказательство.

По определению 2.6 .

.

Но здесь – есть разложение определителя по его первому столбцу, потому является значением . Таковы же все элементы

главной диагонали. Так, – есть разложение определителя по -тому столбцу. Значит, все элементы главной диагонали равны .

Все элементы вне главной диагонали представляют собой суммы произведений элементов какого-либо столбца определителя на алгебраические дополнения соответствующих элементов другого столбца и потому равны нулю.

Значит, .

Пример 2.3.

Для матрицы найти обратную матрицу.

5