Лекции / Лекции по математике / Математика 1 семестр / 12 Кривые второго порядка

Лекция 12

Преобразование прямоугольных координат на плоскости

А) При переходе от системы координат к новой , связь между старыми и новыми координатами некоторой точки плоскости определяется следующими формулами:

(12.1)

Б) При повороте координатных осей

на связь между

старыми и новыми координатами

выражается следующим образом:

c каждой из систем свяжем полярную

систему координат: .

Тогда:

Итак,

(12.2)

.

Замечание 1. Если поворот по часовой стрелке на , то в формуле (12.2) :

(12.2’)

.

Кривые второго порядка

Рассмотрим алгебраическое уравнение второй степени относительно и:

(12.3)

,

где , , т.е. одновременно не равны .

Уравнение (12.3) определяет кривую второго порядка.

1⁰ Окружность.

Определение 12.1.

Геометрическое место точек, равноудаленных от одной точки, называемый центром, называется окружностью.

В выберем произвольную точку , тогда если окружности, то

или

(12.4)

.

Если , то

(12.4’)

.

- каноническое (простейшее) уравнение окружности

Замечание 2.

Если , то окружность стягивается в точку . Если в правой части уравнения (12.4) (), то уравнение определяет мнимую окружность.

Выясним, при каких условиях равенство (12.3) определяет окружность, мнимую окружность или точку.

Для этого преобразуем равенство (12.4):

.

. Заметим (*).

Чтобы уравнения (12.3) при условии (*) привести к каноническому виду (12.4), необходимо выделить полный квадрат относительно и .

Пример 12.1.

Уравнение окружности привести к каноническому виду.

, , , .

2⁰ Эллипс.

Определение 12.2.

Геометрическое место точек, для каждой из которых сумма расстояний до двух данных точек и , называемых его фокусами, есть величина постоянная, и называется эллипсом.

Отметим на оси две точки: , т.е. (фокусное расстояние). Пусть - произвольная точка эллипса.

Фокальными радиусами () точки эллипса называются отрезки прямых, соединяющих эту точку с фокусами и :

(12.5)

, где .

Выведем уравнение эллипса.

. По определению (12.2) имеем:

- иррациональное уравнение.

, , , , , , т.к. , , т.е. ,

Введем обозначение (12.5).

Тогда .

Поделим обе части на (), получим:

(12.6)

.

- каноническое уравнение эллипса.

Если точка не принадлежит эллипсу, то , а это значит, что координаты точки не удовлетворяют уравнению (12.6).

Проведем исследование полученного уравнения, для чего разрешим его относительно . ,

(12.6’)

.

Т.к. и в уравнение эллипса входят в четных степенях, то график функции симметричен как относительно , так и относительно . Т.о. исследование достаточно провести только для I четверти.

При , при . Если на промежутке , то на промежутке . Имеем дугу эллипса, .

Отрезок называется большой полуосью,

отрезок называется малой полуосью.

Замечание 3.

Уравнение (12.6) можно рассматривать и в случае , тогда - большая полуось и фокусы эллипса лежат на оси .

Замечание 4.

В случае, когда , уравнение (12.6) вырождается в окружность с центром в начале координат .

Определение 12.3.

Отношение (фокусного расстояния к длине большой оси) называется эксцентриситетом эллипса и обозначается

(12.7)

Т.к. , то .

Эксцентриситет характеризует форму эллипса (степень сжатия).

Так, если полуось фиксирована, то форма будет зависеть только от расстояния между фокусами. Если фокусы сближаются, то , т.к. . Если фокусы отодвигаются от начала координат, то эллипс сплющивается и когда фокусы совпадают с концами большой оси, эллипс вырождается в отрезок, для которого , т.к. .

Из формул для и , а также (12.6’) можно получить формулы для фокальных радиусов:

(12.8)

.

Если центр эллипса перенести в точку , то уравнение эллипса примет вид: .

Замечание 5.

Уравнение определяет мнимый эллипс.

Уравнение - определяет точку.

Выясним, при каких коэффициентах алгебраическое уравнение (12.3) определяет эллипс, мнимый эллипс или пару мнимых пересекающихся прямых (точку).

, , .

Таким образом, (**).

Пример 12.2.

Уравнение эллипса , привести к каноническому виду.

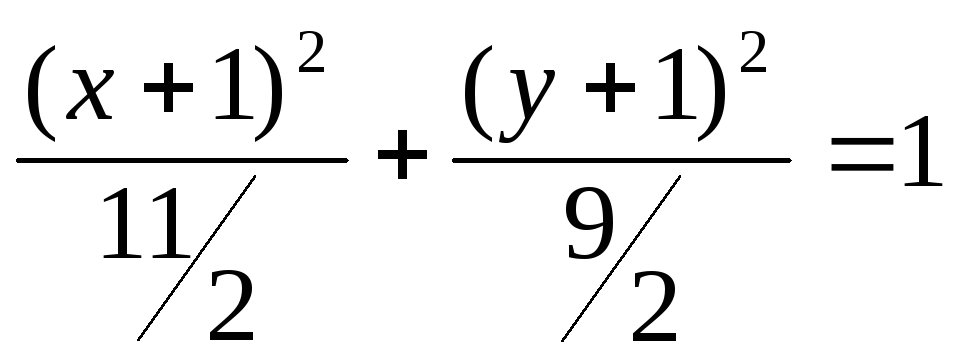, , . Центр: , , , .

2⁰ Гипербола.

Определение 12.4.

Геометрическое место точек, абсолютная величина разности каждой из которых до двух данных точек и , называемых его фокусами, есть величина постоянная, и называется гиперболой.

(12.9)

Из или .

Равенство (12.9) можно переписать в виде: , , , , , ,

(12.10)

.

- каноническое уравнение гиперболы

Если точка не принадлежит гиперболе, то , то это значит, что координаты точки не удовлетворяют уравнению (12.10).

Разрешим уравнение (12.10) относительно : ,

(12.10’)

.

По аналогии с эллипсом проведем исследование только для I четверти (симметрия относительно и ).

. Значит в полосе между прямыми и нет ни одной точки гиперболы.

Покажем, что дуга гиперболы неограниченно приближается к прямой, определяемой уравнением при ее неограниченном удалении от начала координат. Т.е. .

Действительно, .

Гипербола и прямая общих точек не имеют, т.к. система их уравнений не имеет решений.

Итак,

(12.11)

.

- асимптоты гиперболы

6