Добавил:

sava Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Государственный университет — учебно-научно-производственный комплекс (бывш. ОрелГТУ)

Предмет:

Математика

Файл:

20 Непрерывность, точки разрыва, сложная функция

.doc

Скачиваний:

Добавлен:

13.06.2014

Размер:

304.13 Кб

Скачать

☆

Лекция 20

Непрерывность функций в точке

20.1.Основные понятия

Определение 20.1.

Функция определенная в некоторой окрестности точки , включая саму точку, называется непрерывной в этой точке, если

(20.1)

Замечание 1. Таким образом, согласно определению 20.1. предел функции и ее значение в точке равны.

Определение 20.2.

Функция f(x) непрерывна в точке тогда и только тогда, когда для любой последовательности из некоторой окрестности точки , сходящейся к , соответствующая последовательность сходится к .

Определение 20.3

непрерывна в точке тогда и только тогда, когда:

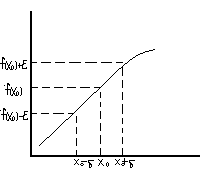
Пусть .

Тогда величина называется приращением аргумента.

называется приращением функции.

Преобразуем формулу (20.1):

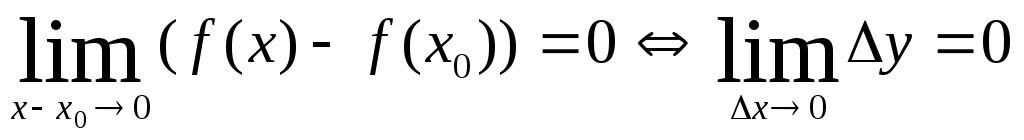Определение 20.4.

Функция f(x) называется непрерывной в точке , если ее приращение в этой точке является бесконечно малой функцией при

Замечание 2. Определения 20.1-20.4 эквивалентны.

Теорема 20.1.

Пусть функции и непрерывны в точке . Тогда , (если) также непрерывны в этой точке.

20.2. Непрерывность элементарных функций

Простейшие элементарные функции:

Замечание 3. Арифметические действия от этих функций назовем элементарными функциями.

Пример 20.1.

Показать, что , , , - непрерывные функции.

а) . .

б). 1). Докажем для :

Поэтому .

2). В силу теоремы 20.1 - непрерывная функция, т.к.

в).

г). .

Замечание 4. 1) ;

20.3. Гиперболические функции

Гиперболическими называются следующие функции:

- гиперболический синус,

- гиперболический косинус,

- гиперболический тангенс,

- гиперболический котангенс.

Гиперболические функции являются непрерывными функциями (это следует из непрерывности показательных функций).

Имеют место следующие формулы:

Сложная функция

Определение 20.5

Пусть заданы функции : область определения функции f(x) содержит область значений функции (x).

Тогда определена функция называемая сложной функцией.

Теорема20.1.

Если непрерывна в точке , а непрерывна в точке , то непрерывна в точке .

Доказательство:

(в силу непрерывности функции).

Также в силу непрерывности функции имеем:

т.е. .

Теорема20.2 (об ограниченности непрерывных функций).

Если функция f(x) непрерывна в точке , то существует окрестность этой точки, на которой f(x) ограничена.

Доказательство:

20.5. Обратная функция

Определение 20.6.

Пусть X и Y - некоторые множества и задана функция f(x), т.е. множество пар чисел (x, y): , причем.

Если в каждой паре множества числа х и у поменять местами, то получим (у; х):.

Данное множество называется обратной функцией к функции .

Обозначение:.

Определение 20.7

Пусть функция f(x) определена на множестве и пусть.

Тогда говорят, что

а) не возрастает, если ; б) не убывает, если ;

в) возрастает, если ; г) убывает, если .

Замечание 5. Такие функции называются монотонными.

В случаях в) и г) говорят, что f(x)-строго монотонная функция.

Теорема 20.2 (о непрерывности обратной функции).

Пусть функция , определена, строго монотонна и непрерывна на некотором промежутке и пусть - множество ее значений. Тогда на множестве обратная функция однозначна, строго монотонна и непрерывна.

20.6. Точки разрыва функции

Определение 20.8.

Пусть функция f(x) определена на интервале (а;b); кроме может быть точки . Точка называется точкой разрыва функции , если функция не определена в точке , или если она определена в этой точке, но не является в ней непрерывной.

Определение 20.9.

Будем говорить, что функция f(x) непрерывна в точке справа (слева), если:

Теорема 20.3.

Функция непрерывна в точке , если она определена в некоторой окрестности этой точки и в самой точке и существуют пределы:

Определение 20.10.

Если - точка разрыва функции и существуют конечные пределы

то точка называется точкой разрыва первого рода. Величина называется скачком функции в точке .

Если , то точку называют точкой устранимого разрыва (т.е. ее можно доопределить до непрерывной функции).

Определение 20.11.

Точка разрыва функции , не являющаяся точкой разрыва первого рода, называется точкой разрыва второго рода (к примеру, один из односторонних пределов не существует или равен бесконечности).

Пример 20.2.

( - разрыв второго рода);

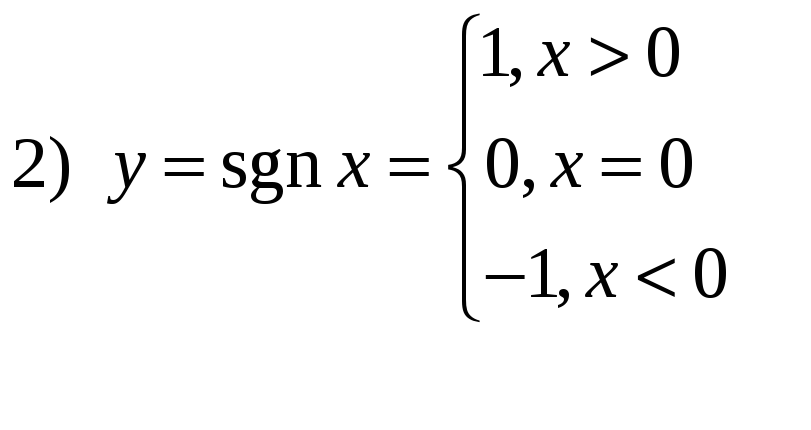.( - разрыв первого рода);

(устранимый разрыв)

20.7. Свойства функций, непрерывных на отрезке

Определение 20.12.

Функция, определенная на отрезке и непрерывная в любой точке этого отрезка, называется непрерывной на этом отрезке (причем должна быть непрерывность на границах: слева справа соответственно).