Лекции / Лекции по математике / Математика 1 семестр / 18 Функции. Предел функции

Лекция 18

Число е

Рассмотрим последовательность {x_n} с общим членом .

Докажем, что она сходится.

Для этого достаточно доказать:

1. {x_n} возрастающая;

2. {x_n} ограничена сверху.

Рассмотрим и докажем, что последовательность {y_n} убывает, т.е .

Докажем, что она сходится.

Доказательство

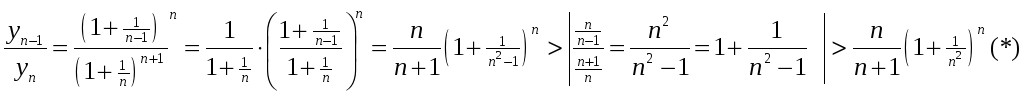
Замечание1. Неравенство (*) верно: знаменатель увеличили, дробь уменьшилась.

Обозначим .

Итак, , т.е. последовательность {y_n} убывающая.

Так как , то последовательность ограничена, т.е. существует предел последовательности .

Замечание2. В доказательстве использовалась формула суммы бесконечно убывающей геометрической последовательности:

Обозначим …

Таким образом .

называют вторым замечательным пределом

Функции одной переменной

1. Понятие функции

Определение 18.1.

Пусть x и y – некоторые числовые множества. Если каждому элементу множества X единственным образом соответствует элемент множества Y, то это соответствие называется функцией.

Обозначение: .

Здесь y – зависимая переменная, х – независимая переменная (аргумент)

X – обл. определения (существования) функции (D(f));

Y – множество значений функции (E(f)).

Определение 18.2.

Пусть f(x) определена на некотором множестве X.

f(x) ограничена сверху (снизу), если:

.

Условие ограниченности:.

Пример 18.1.

Показать, что – ограниченная функция.

().

2. Способы задания функции

1. Аналитический

При аналитическом способе задания функция задается с помощью формул:

А) в явном виде

Функция разрешена относительно y: .

Б) в неявном виде

Функция не разрешена относительно y:.

В некоторых случаях от неявно заданной функции можно перейти к явному виду, иногда это сделать невозможно:

Пример 18.2.

.

При аналитическом способе функцию можно задать:

а) несколькими выражениями:

Пример 18.3. Signum (лат.)-знак.

б) параметрически:

Пример 18.4. .(график функции – астроида)

в) в полярной системе координат:

Пример 18.5. – уравнение лемнискаты Бернулли.

18.2.2. Табличный

			…
			…

(Например, расписание поездов).

2. Графический

Соответствие между аргументом и функцией задается посредством графика.

Замечание. Окружность, заданная формулой , не является графиком функции (это график уравнения), однако полуокружности, заданные уравнениями , являются графиками функций.

18.3. Классификация элементарных функций

Основные элементарные функции

а) тригонометрические:

;

б) обратные тригонометрическим:

;

в) степенная: ;

г) показательная: ;

д) логарифмическая: .

Все функции, получаемые с помощью конечного числа арифметических действий над элементарными функциями, а также суперпозицией (или наложением) этих функций составляют класс элементарных функций.

Пример 18.6.

Примеры элементарных функций: .

Классификация элементарных функций

. Функция вида , где называется целой рациональной функцией или алгебраическим многочленом степени .

. Функция вида называется дробно-рациональной.

. Функция, полученная с помощью конечного числа суперпозиций и арифметических действий над степенными функциями, не являющаяся рациональной, называется иррациональной функцией:

,

. Функция, не являющаяся рациональной или иррациональной, называется трансцендентной функцией:

.

3. Предел функции

18.3.1. Предел функции в точке .

Определение 18.3. (на языке последовательностей)

Пусть функция f(x) определена на множестве X. Пусть также заданы: последовательность причем ,

а также соответствующая последовательность причем тогда .

Или: .

Пример 18.7.

Доказать, что функция не имеет предела.

Построим при . Тогда .

Но если построить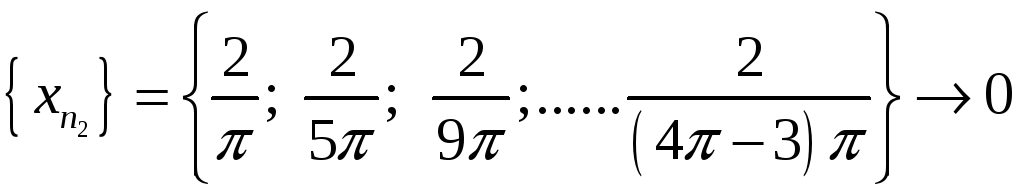, при , но

Таким образом, для двух сходящихся последовательностей, соответствующие последовательности значений функции имеют разные пределы.

Определение 18.3 (предела функции в точке на языке эпсилон-дельта ())

Число A называется пределом функции f(x) в точке, если:

удовлетворяющих неравенству , выполняется неравенство .

Или : .

Замечание 3. Оба определения предела функции эквивалентны.

Геометрический смысл понятия «предел функции»

Пусть М – произвольные точки графика функции .

Точки М графика должны находиться в полосе шириной , ограниченной прямыми , , для всех значений x, удаленных от точки не далее чем на .

Пример 18.8.

.

4. Односторонние пределы

Определение 18.4.

Если у любой сходящейся к точке последовательности все ее элементы меньше , а соответствующая последовательность сходится к , то число называется левым пределом функции .

Обозначение: .

Определение 18.5.

Если у любой сходящейся к последовательности все ее элементы больше , а соответствующая последовательность сходится к , то число называется правым пределом функции f(x):

Обозначение: .

Утверждение.

Функция имеет предел в точке тогда и только тогда, когда в этой точке существуют пределы справа и слева и они равны .

Пример 18.9.

. Найти .

.

.

6