Лекции / Лекции по математике / Математика 1 семестр / 15 Задачи и поверхности 2го порядка

Лекция 15

6⁰. Некоторые задачи на прямую и плоскость в пространстве

1). Найти угол между прямой и плоскостью.

Углом между и называется угол между и ее проекцией на .

. . Тогда

(15.1)

или .

2). Написать уравнение перпендикуляра, опущенного из точки на прямую , заданную уравнением и найти расстояние от точки до прямой.

Построим плоскость , содержащую точку и прямую . Уравнение этой плоскости имеет вид: Построим также плоскость , проходящую через точку , перпендикулярно прямой :

.

Система этих двух уравнений и дает искомый перпендикуляр.

. (15.2)

3). Написать уравнение общего перпендикуляра к двум скрещивающимся прямым и .

Пусть , и , , тогда - является направляющим вектором искомого перпендикуляра.

а) - вектор нормали плоскости , которая содержит прямую и (или содержит искомый перпендикуляр).

,

Система этих двух уравнений задает искомый перпендикуляр.

Замечание: 1) , т.е. .

2) , т.е. .

Поверхности II порядка

Алгебраическое уравнение II степени относительно 3-х переменных вида:

(*)

,

где , ,

определяет поверхность II порядка.

Будем изучать случаи, когда . Уравнение (*) при перечисленных условиях может определять сферу, эллипсоид, параболоид, цилиндрическую поверхность, коническую поверхность и гиперболоиды в зависимости от коэффициентов.

I тип задач

(по геометрическим свойствам поверхности определяется уравнение)

1. Сфера

Определение 15.1.

Множество точек пространства, равноудаленных от данной точки , называемой центром, называется сферой.

Выберем произвольную точку принадлежащую сфере, тогда или

(15.3)

- каноническое уравнение сферы с центром и радиусом .

2. Цилиндрические поверхности

Определение 15.2

Цилиндрической поверхностью называется поверхность, описываемая прямой (образующей), движущейся вдоль некоторой линии (направляющей) и остающейся параллельной исходному направлению.

Если , то - определяет линию в плоскости .

(не содержит переменной ).

Цилиндром II-го порядка называется цилиндрическая поверхность, направляющими которой являются эллипс, гипербола, парабола:

А) Эллиптический цилиндр.

Б) Гиперболический цилиндр.

В) Параболический цилиндр.

3. Конические поверхности

Определение 15.3

Поверхность, образованная прямыми, пересекающимися в одной точке и проходящими через каждую точку линии - называется конической поверхностью.

II тип задач

(по виду уравнения определяются свойства поверхности)

Основным методом решения таких задач является метод сечений, который заключается в поиске линий пересечений данной поверхности плоскостями, параллельными координатным плоскостям.

4. Эллипсоид

Определение 15.4.

Эллипсоидом называется поверхность, которая в прямоугольной системе координат определяется уравнением

. (15.4)

Установим геометрический вид эллипсоида.

Рассмотрим сечения эллипсоида плоскостями параллельными ( число).

Линия сечения определяется системой:

(**)

.

Исследуем (**).

А) , тогда - эллипс в плоскости , причем самый большой.

Б) , тогда - линия (**) вырождается в точки .

(плоскости касаются эллипсоида)

В) , тогда .

Таким образом, плоскость пересекает эллипсоид по эллипсу, причем, если , то , поэтому при , получается самый большой эллипс.

Г) , то - мнимый эллипс, точек пересечения с не .

- полуоси эллипсоида. Если , то эллипсоид является сферой.

Аналогично, если или .

5. Однополостной гиперболоид

Определение 15.5

Однополостным гиперболоидом называется поверхность, которая в прямоугольной системе координат определяется уравнением

. (15.5)

Установим его геометрический вид.

Рассмотрим сечения с координатными плоскостями:

и 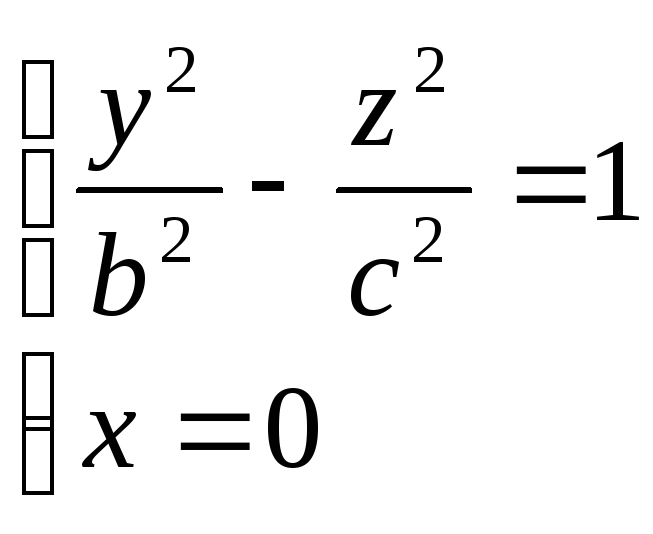(В сечения получаются гиперболы)

Также рассмотрим сечения поверхности плоскостями :

.

А) , - самый маленький эллипс.

Б) , .

В) , , 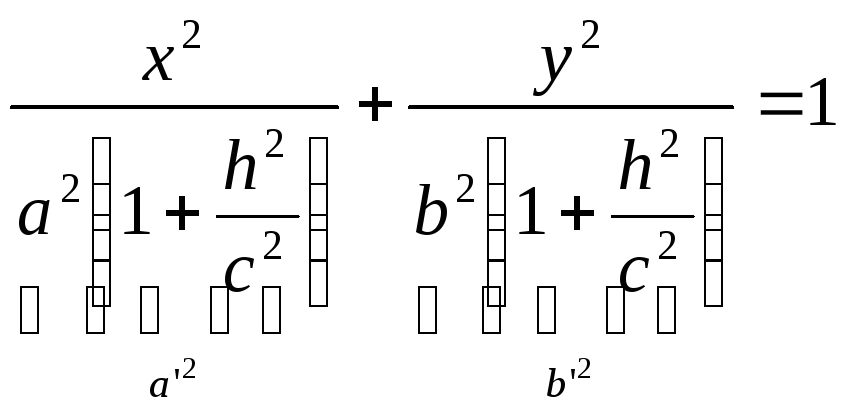, то .

Г) , , то .

Таким образом, рассмотренные сечения позволяют изобразить однополостной гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления. - полуоси (чтобы изобразить , следует построить основной прямоугольник какой-нибудь из гипербол).

6