
- •Свойства операции умножения матриц:
- •5.1.2. Уравнения линии
- •5.2.2. Неполные уравнения плоскостей
- •5.2.3. Уравнение плоскости «в отрезках»
- •5.2.4. Нормальное уравнение плоскости
- •5.2.5. Расстояние от точки до плоскости
- •5.2.7. Угол между двумя плоскостями
- •5.3.1. Векторное уравнение прямой
- •5.3.2. Параметрические уравнения прямой
- •5.3.3. Канонические уравнения прямой
- •5.3.4. Уравнения прямой, проходящей через две данные точки
- •5.3.5. Общие уравнения прямой
- •5.4.1. Точка пересечения прямой и плоскости
- •6.1.1. Расстояние между двумя точками
- •6.1.2. Деление отрезка в данном отношении
- •6.2.2. Каноническое уравнение прямой
- •6.2.3. Уравнение прямой, проходящей через две точки
- •6.2.5. Уравнение прямой в отрезках
- •6.2.6. Нормальное уравнение прямой
- •6.2.8. Координаты точки пересечения двух прямых
- •6.2.9. Угол между двумя прямыми
- •6.3.1. Эллипс
- •6.3.2. Окружность
- •6.4.1. Параллельный перенос
- •6.4.3. Изменение начала координат и поворот осей
- •6.5.1*. Полярные координаты на плоскости
- •6.5.2*. Связь полярных координат с декартовыми
- •6.5.3*. Уравнения линий в полярной системе координат
- •6.6*. Параметрическое задание линий
- •6.6.1*. Окружность
- •6.6.2*. Циклоида
- •6.6.3*. Астроида
- •7.5.1. Эллипсоид
- •Гиперболоиды
- •7.5.2. Однополостный гиперболоид
- •Параболоиды
- •7.5.4. Эллиптический параболоид
- •7.5.5. Гиперболический параболоид
- •7.5.6. Конус
- •Цилиндры
- •7.5.7. Эллиптический цилиндр
- •7.5.8. Гиперболический цилиндр
- •7.5.9. Параболический цилиндр
- •Примеры числовых множеств:
- •8.1.5. Связь полярных координат с декартовыми
- •Метод Лагранжа
- •16.4.1. Производная векторной функции скалярного аргумента
- •16.4.2. Уравнение касательной к пространственной кривой
- •16.4.4. Касательная плоскость и нормаль к поверхности
Определенный интеграл
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S = 4S = 4∫2 |
ab sin2 tdt = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
sin 2t |
π |
= πab. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
02 |
|
|
|
|
|
|
|
|
||||||
|
|
= 2ab∫(1−cos 2t )dt = 2ab t − |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример: |
|
Найти площадь фигуры, |
|
ограниченную первой |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
2a |
y |
|||||||||||||||||||||
|
|
аркой циклоиды х = а (t − sin t); у = а (1 − cos t) и |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
отрезком оси абсцисс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Точкам О и А соответствуют значения параметра |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
tО = 0 и tА = 2π, поэтому искомая площадь равна |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
S= |
2π a (1−cost ) a |
(1−cost ) dt = |
2π a2 (1−cos t )2 dt = |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
∫ |
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2π |
2 |
|
1+cos 2t |
|
|
|
2 |
3 |
t −2sin t + |
1 |
|
|
|
|
2π |
||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
a |
1−2cos t + |
|
|
|
|
dt = а |
|
|
|
|
sin 2t |
|
|
|
|||||||||
|
|
|
∫0 |
|
|
2 |
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
8.1.4. Полярные координаты на пло ко ти |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|||||
Полярные координаты определяют я заданием |
|
|
|
|
|
|
|
|
||||||||||||||||||
на плоскости полюса О и полярной о и ρ . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Координаты точки М в полярных координатах за- |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
JJJG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
даются длиной радиус-вект ра |
|
|
с |
|
= ρ этой точки |
|
|
|
|
|
|
|
|
|||||||||||||
OM |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
и углом его наклона к п лярн й |
|
си. |
При этом |
|
|
|
|
|
|
|
|
|||||||||||||||
0 ≤ ρ < ∞, 0 ≤ϕ ≤ ∞ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
8.1.5. Связь полярных координат с декартовыми |
|
|
|
|
|
|
|
|
||||||||||||||||||
Совместим н ч ло дек ртовой системы с по- |
|
|
|
|
|
|
|
|
||||||||||||||||||
люсом полярной системы координат, а ось Оx с по- |
|
|
|
|
|
|
|
|
||||||||||||||||||
лярной осьюρ . |
Найдём связь координат |
|
точки |
|
|
|
|
|
|
|
|
|||||||||||||||
M(x,y) и M( ρ ,ϕ). Она выражается следующей сис- |
|
|
|
|
|
|
|
|
||||||||||||||||||
темой ур внений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x = ρ cosϕ, |
ρ = |
x2 + y2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y = |
ρsinϕ, |
tgϕ = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Скачано |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
. |
ru |
πa
= 3πa2.
259
x
2πa

260 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
Лекции 7 - 8 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
8.1.6. Примеры уравнений линий в полярной системе координат |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
Уравнение вида ρ = ρ(ϕ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
, определяет на |
|||||||||||||||||||||
|
|
задающее ρ как функцию ϕ |
|||||||||||||||||||||||||||||||||||||||||||
|
плоскости некоторую кривую. |
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Архимедова спираль: ρ =аϕ, 0 <ϕ < ∞, ρ ≥ 0 . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
ϕ |
|
|
0 |
|
|
|
|
|
|
π |
|
|
|
|
π |
|
|
|
2π |
|
|
|
5π |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
ρ |
|
|
0 |
|
|
|
|
|
|
|
|
π |
|
|
|
|
a π |
|
|
2aπ |
|
|
5aπ |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
a 2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кривая представляет собой путь, |
описываемый точкой, движущейся с |
||||||||||||||||||||||||||||||||||||||||||
|
! |
||||||||||||||||||||||||||||||||||||||||||||
|
|
постоянной скоростью по лучу, вращающемуся около полюса О, с по- |
|||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
стоянной скоростью ω : a = |
|
v |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Окружность со смещенным центром: |
ρ = a cosϕ . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
ϕ |
0 |
|
|
|
|
π |
|
|
|
|
π |
|
π |
|
3π |
|
|
|
|
7π |
|
2π |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
cosϕ |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
0 |
|
-1 |
|
|
0 |
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Скачано |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
ρ |
a |
|
|
|
|
|
2 |
a |
|
|
|
|
0 |
|
0 |
|
|
0 |
|
|
|
|
2 |
a |
|
a |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Координата ρ принимает только положительные значения. |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
Поскольку cosϕ = |
|
ρ |
|
значит, угол ОМА - прямой. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Вывод: |
урав е ие ρ = a cosϕ |
|
задает |
окружность |
|
с центром в точке |
||||||||||||||||||||||||||||||||||||
|
|
|
(a/2,0) и р диусом a/2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
Преобр зуем: |
ρ = a cosϕ , ρ ρ = a ρ cosϕ ; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
ρ2 |
= aρ cosϕ ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x2 +y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + y2 = ax ; x2 + y2 −ax + a2 − a2 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
a 2 |
+ y |
2 |
|
|
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
- каноническое уравне- |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
x − |
|
|
|
= |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
ние окружности с центром в точке ( a |
,0) радиусом |
a . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||

Определенный интеграл
8.1.7. Площадь криволинейного сектора в полярной системе
i |
|
Пусть |
ρ = ρ(ϕ) |
|
|
- непрерывная функция. Опре- |
|
|
. |
|||||||||||||||||||||||||||||||||||
|
|
|
i |
|
i |
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
i |
|
|
|
i |
|
|
|
|
antigtu |
||||||||||||||
делим площадь криволинейного сектора, ограничен- |
|
|
||||||||||||||||||||||||||||||||||||||||||
ного кривой ρ = ρ |
(ϕ) и лучами ϕ =α , ϕ = β . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Разобьем указанный сектор лучами на сектора вели- |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чины +ϕi . Пусть |
|
ρi |
|
|
= ρi |
- величина радиус-вектора |
|
|
|
|||||||||||||||||||||||||||||||||||
для произвольного |
ϕi |
[ϕi ,ϕi+1 ]. |
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
||||||||||||||||||||||||
Лемма: Площадь кругового сектора равна Sα |
= |
2 |
α . |
|
|
|
||||||||||||||||||||||||||||||||||||||
Доказательство следует из пропорции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
Sкруга =πr2 → 2π; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
Sα → α; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Sα |
= |
απr2 |
= |
|
αr |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2π |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Si |
|
равна |
|
|
|
||||||||
Тогда |
|
|
площадь |
|
|
кругового |
|
|
|
сектора |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
S = |
1 |
ρ |
2 |
+ϕ ; сумма Q = |
|
n |
|
1 |
ρ |
2 |
+ϕ |
|
- площадь ступен- |
|
|
|
||||||||||||||||||||||||||||
2 |
|
i=1 |
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
чатого сектора, спрямляющего криволинейный сек- |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то- |
|
|
|
|||||||||||||||||||
тор. При |
n →∞ Q → S , |
|
Q |
|
- интегральная сумма, |
|
|
|
||||||||||||||||||||||||||||||||||||
гда S |
= |
1 |
β |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример: |
|
|
Вычислить площ дь круга ρ = 2a cosϕ . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
В силу симметрии достаточно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
вычислить 1/2 искомой площади. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
S = 2 π∫/ 2 |
ρ2dϕ = π∫/ 2 (2a)2 cos2 ϕdϕ = π∫/ 2 |
4a2 1+cos 2ϕ dϕ = |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
π / 2 |
dϕ |
|
π |
/ 2 |
|
cos 2ϕ |
|
|
|
2 |
ϕ |
|
|
π / 2 |
|
1 |
|
π |
/ 2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
= 4a |
+ ∫ |
|
|
|
|
+ |
sin 2ϕ |
= |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
2 |
|
|
|
2 |
|
|
dϕ = 4a |
|
|
2 |
|
|
0 |
4 |
0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
= 4a |
2 |
|
π |
|
−0 + |
1 |
sin π |
− |
1 |
|
|
= 4a |
2 π |
=πa |
2 |
. |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
4 |
4 |
sin 0 |
|
4 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример:
ru |
261 |
|
координат
4 |
|
|
2 ∫ |
|
|
|
|
2 |
2 |
|
|
|
4 |
|
|
ru |
|
|
|
|
|
|
|
|
||
262 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекции 7 - 8 |
||||||
|
Найти площадь, заключённую внутри лемнискаты Бернулли |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
ρ2 = а2 сos2ϕ . |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
В силу симметрии достаточно |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
||||||||||
|
вычислить одну четверть искомой площади: |
|
|
|
|
|
|
|
2a |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
l = +x2 ++y2 = |
1+ +yi 2 |
+x |
- |
длинаantigtui - хорды, |
|
|
|
|
a |
|
|
x |
|
|
||||||||||||
1 |
S = |
1 |
π 4 |
2 |
cos 2ϕdϕ = |
a2 sin 2ϕ |
|
π 4 |
= |
a 2 |
, |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
0 |
|
2 |
. |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда S = а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8.2. Вычисление длины дуги кривой
8.2.1. Вычисление длины плоской кривой в прямоугольных координатах
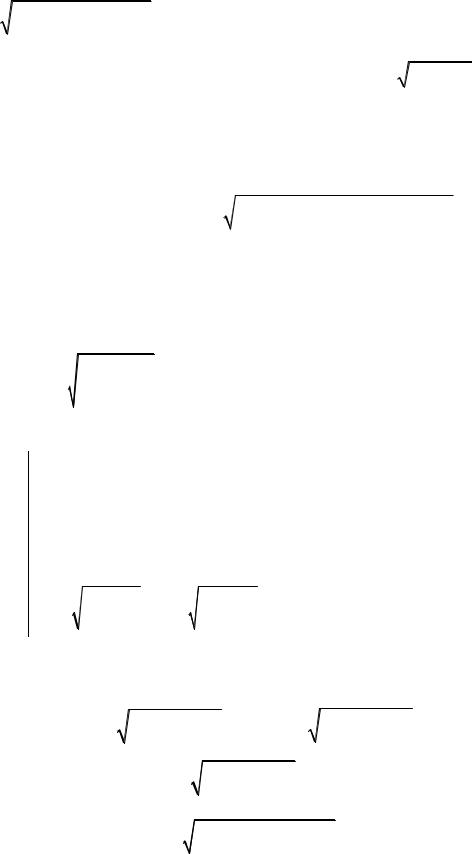
L : y = f (x). |
|
|
|
Разобьем |
|
|
|
|
[a,b] |
|
на |
|
части |
|
|
|
|
|
|||||||||||||||||||||||||
a = x0 < x1 < x2 <... < xn = b . |
|
|
A, M1,..., Mn−1, B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
На кривой обозначим точки |
|
Соеди- |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
ним их хордами. Получим ломаную, |
состоящую из n |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
хорд. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
i |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln = ∑li - длина ломаной. По теореме Лагранжа ( f (b)− f (a) = f '(c)(b − a)) |
|||||||||||||||||||||||||||||||||||||||||||
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеем: +yi = f |
'(ξ |
) |
|
|
|
|
[x − , x |
], l |
|
|
|
|
n |
1 + f '(ξ |
|
) |
|
|
|
|
|
|
|
||||||||||||||||||||
, ξ |
|
n |
= |
∑ |
i |
2 |
+x . |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
+xi |
|
|
|
i |
|
|
|
i |
|
|
i 1 |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть max+xi → 0 , |
ln → l , следовательно, |
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
l = |
|
1 + |
f '(x) 2 dx . |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
8.2.2. Вычисление длины плоской кривой в параметрической форме |
|||||||||||||||||||||||||||||||||||||||||||
|
x = x(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
L : |
|
|
|
|
|
α ≤ t ≤ β |
|
(a = x(α);b = x(β )); |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
= y(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
( |
|
) |
|
|
|
b |
|
|
|
|
[ |
|
|
x |
] |
|
|
{ |
|
|
|
( |
|
|
) |
|
|
|
|
} |
|
||||||
l = |
|
∫ |
|
|
x |
|
|
|
∫ |
|
1+ |
y |
|
|
x |
= x |
t |
, dx = x ' dt |
= |
||||||||||||||||||||||||
|
|
1+ f ' |
|
|
2 dx = |
|
|
|
|
' |
2 dx = |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= β |
|
1 |
+ |
[ |
y |
' 2 x ' |
( |
t |
) |
dt = |
y |
|
' |
= dy |
= |
|
yt ' |
= |
β |
|
x ' |
( |
t |
|
2 + y ' |
( |
t |
|
2 dt , |
||||||||||||||
|
|
|
|
∫ |
|
|
|||||||||||||||||||||||||||||||||||||
∫ |
|
|
|
x ] |
|
|
|
|
|
|
|
x |
|
|
|
dx x ' |
|
|
|
|
|
|
|
) |
|
|
|
) |
|||||||||||||||
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определенный интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
263 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
β |
x'(t ) 2 |
|
|
|
|
|
(t ) |
2 dt . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||||
|
l = |
∫ |
+ y ' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
Если кривая задана в полярных координатах, то l |
= ∫ |
ρ2 + ρ′2 dϕ |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
8.2.3. Вычисление длины дуги пространственной кривой |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
в параметрической форме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
x = x(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
( |
t |
) |
α ≤ t ≤ β , |
l = |
∫ |
|
|
|
|
( |
t |
) |
|
|
( |
t |
|
) |
|
|
( |
t |
) |
2 dt |
|
|
||||||||||||||
|
|
L : y = y |
|
|
|
|
|
|
x ' |
|
2 |
+ y ' |
|
|
|
2 + z ' |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
z = z (t ) |
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L : y = ln 1− x2 |
) |
; a = 0,b = 1 ;l −? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
|
|
4x2 |
|
|
|
|
|
|
2 x2 +1 |
|
|
|
|
1+ x |
|
|
|
|
|
1 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
l = |
|
|
1+ |
|
|
|
|
|
|
|
|
dx = |
|
|
|
|
|
|
dx = −x +ln |
|
|
|
|
|
|
02 = ln 3 − |
|
|
|
|
|
||||||||||||
|
|
|
|
∫ |
( |
|
|
|
|
) |
2 |
∫1− x |
2 |
|
|
|
x −1 |
2 . |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
1− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Пример: |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
= a cos t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
= a sin t |
|
- винтовая линия. lвитка =? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
= 2π t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
l = 2∫π |
a2 + |
|
c |
2 dt = 2π a2 + |
|
|
c 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
4π |
|
|
|
|
|
|
|
|
|
|
|
4π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8.2.4. Дифференци л длины дуги кривой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
l (x) |
= x |
|
1 + f '(x) 2 dx ; l '(x)= 1+ f '(x) 2 |
|
; |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dl = 1+ f '(x) 2 dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В параметричес ой форме: dl = |
|
x'(t ) 2 |
+ y '(t ) 2 dt . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеющей длину l = |
x '2 + y '2 dt , l = x ' (ϕ) 2 + y ' (ϕ) |
2 dϕ . |
ru |
|
264 |
|
|
|
Лекции 7 - 8 |
8.2.5. Длина кривой, заданной в полярных координатах |
. |
|
|
|
α |
α |
|
|
|
Пусть уравнение кривой в полярных координатах ρ = ρ(ϕ). Можно рас- |
||||
сматривать уравнения x = ρ cosϕ как параметрические уравнения линии L, |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
y = ρsinϕ |
|
|
antigtu |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
t |
|
|
|
t |
|
|
|
|
|
∫ |
|
|
|
|
|
|
||||
|
x 'ϕ = ρ 'cosϕ − ρsinϕ , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y 'ϕ = ρ 'sinϕ + ρ cosϕ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x 'ϕ |
2 + y 'ϕ |
2 = (ρ 'cosϕ − ρ sinϕ )2 + (ρ 'sinϕ + ρ cosϕ)2 |
= ρ '2 + ρ2 , |
|||||||||||||||||||||||
|
|
β |
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l = ∫ (x 'ϕ )2 + (y 'ϕ )2 dϕ = ∫ ρ '2 + ρ2 dϕ . |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
α |
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Вычислить длину окружностиρ = 2a cosϕ . |
|
|
|
|||||||||||||||||||
|
|
|
|
|
π / 2 |
( |
−2a sinϕ)2 + 4 |
|
|
|
|
|
|
π / 2 |
|
|
|
||||||||||
|
|
|
|
|
L = 2 ∫ |
2 cos2 ϕdϕ = 4 ∫ |
cos2 ϕ +sin2 ϕdϕ = |
||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
= 4aπ∫/ 2 dϕ |
|
|
|
|
|
|
|
|
|
π = 2πa. |
|
|
|
|
|
|||||||
|
|
|
|
|
= 4a ϕ |
π0 / 2 = 4a |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8.2.6. Площадь поверхности вращения |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
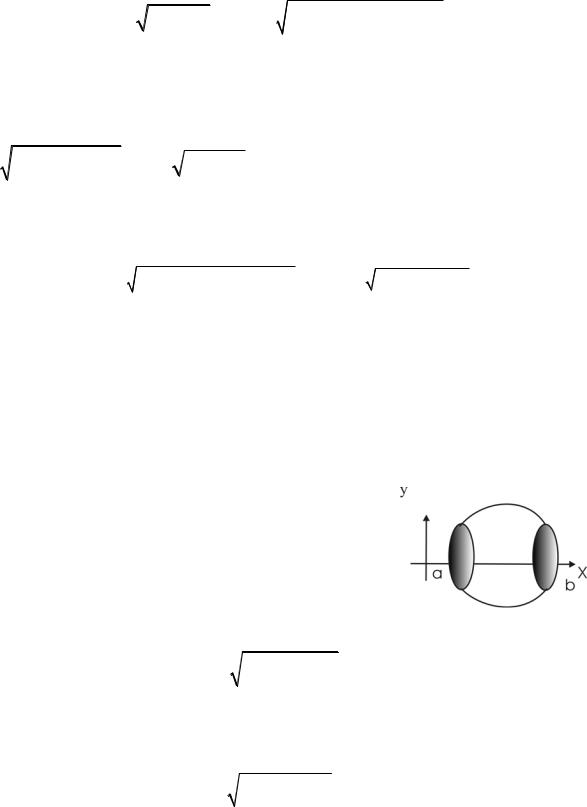
Вычислим Qx – площадь поверхности, образованной вращением кривой |
|||||||||||||||||||||||||
|
y = f (x) вокруг оси Ох). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Разделим отрез к [a, b] |
|
т чками деления xi . |
|
|
|
||||||||||||||||||||
Точке xi |
соответствует точка |
|
а кривой Mi . |
|
|
|
|
||||||||||||||||||||
|
|
Соединим точки |
а кривой хордами (li ). |
|
|
|
|||||||||||||||||||||
|
При вращении к жд я хорда описывает усечен- |
|
|
|
|||||||||||||||||||||||
|
|
ный конус. Площ дь его поверхности: |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
Q = |
2π |
yi−1 + yi |
l ; |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
i |
|
|
|
|
2 |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qi = 2π |
yi−1 + yi |
|
1+ f |
'(ξi |
) 2 +xi ; |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Qn |
= ∑Qi ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
max+xi → 0 ; Qn |
→ Qx . |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
n |
|
|
|
|
b |
|
|
( |
|
|
) |
|
|
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
→ 2π |
∫ |
f |
x |
|
|
|
x |
|
|
|
||||||||||||
|
|
|
|
|
Q |
|
|
|
|
1 + f ' |
|
|
2 dx |
|
|
|
|||||||||||
a

Определенный интеграл |
|
|
265 |
||||||
|
b |
|
( |
|
) |
|
( |
|
2 dx - площадь поверхности, образованной враще- |
Q = 2π |
∫ |
f |
x |
1 + f ' |
x |
||||
x |
|
|
|
|
) |
||||
|
a |
|
|
|
|
|
|
|
|
нием кривой, заданной функцией у = f (x), а ≤ х ≤ b . |
|||||||||
Если дуга задана параметрическими уравнениями х = х (t), у = у (t), t1 ≤ t ≤ t2 ,
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
ru |
|||
то Qх |
= 2π |
|
y(t ) |
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
(t ) dt . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
∫ |
|
x |
(t ) |
|
+ y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если дуга задана в полярных |
|
координатах |
|
|
ρ |
= |
|
ρ |
|
(ϕ), |
α ≤ ϕ ≤ β, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
то Qх |
= 2π |
β |
ρ(ϕ)sinϕ |
|
|
|
ρ2 + ρ′(ϕ) 2 dϕ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Найти площадь поверхности, образованной вращением астроиды х2/3 + |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
у2/3 = а2/3 вокруг оси Ох. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a2 3 − x2 3 )1 2 |
|||||||||||||
|
|
|
|
|
|
2/3 |
|
|
|
2/3 3/2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
2/3 |
|
|
|
2/3 |
|
½ |
|
|
|
|
|
|
2 |
|
х |
−1/3 |
|
|
|
||||||||||||||||||||||
|
|
|
|
у = (а |
|
− |
х ) , у′ |
= |
|
|
(а |
|
|
|
|
− |
х ) |
|
|
( |
− |
|
|
|
) = − |
|
|
|
x1 3 |
|
, |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1+ a 2 3 − x 2 3 |
= |
a1 3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
x 2 3 |
|
|
|
|
|
|
|
|
x |
|
1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
Следовательно Q |
х |
= 2 2π a |
( |
a2 3 − x2 3 |
) |
|
a1 3 |
dx = |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 3 a |
|
|
2 3 |
|
|
|
2 3 |
|
3 2 |
|
|
−1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1/3 3 (a 2 3 − x 2 3 )5 2 |
|
a |
|
12 |
2 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
= 4πa |
∫(a |
|
|
|
− x |
|
|
|
|
|
|
) |
|
|
|
x |
|
|
|
|
dx = |
− 4πа |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
5 |
πа |
. |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
5 2 |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Найти площадь п верхн сти, |
образованной вращением одной арки цик- |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
лоиды х = а (t − sin t), у = а (1− cos t) вокруг оси Ох. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Реше ие: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Диффере цируем х′ = а (1 − cos t), у′= а (sin t), |
|
|
|
|
|
|
|
|
t |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
′ |
) |
2 |
|
|
′ |
) |
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
(1−cos t ) |
2 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
2(1 − cos t) |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
+ |
|
|
|
= |
|
|
|
|
|
|
a |
|
|
|
+ a |
|
|
sin |
|
|
t = а |
= 2а sin 2 . |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
(x |
|
(y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
2 |
2π |
|
|
|
|
2 t |
|
|
|
t |
|
|
|
|
|
|
|||||
|
|
|
|
Qх = 2π ∫ a (1−cos t )2a sin |
|
|
|
dt = 8πа |
|
|
∫ |
1−cos |
|
|
sin |
|
dt |
= |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
2 |
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
3 t |
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
− |
|
|
2 |
|
|
|
|
64 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
= − 16π |
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
πа |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
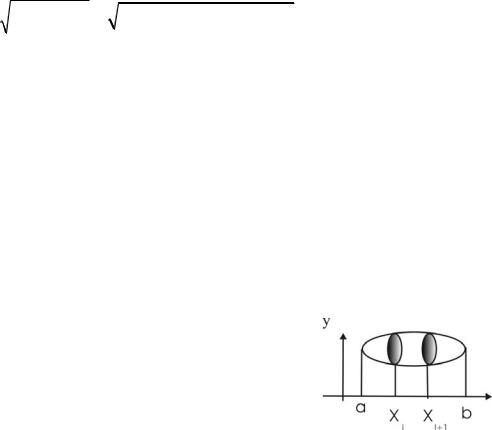
266 |
|
((ρ′)2 |
+ ρ2 )= |
4a2 (1+ cosϕ)2 + 4a2 sin2 ϕ = 4а сos ϕ . |
|
ru |
Лекции 7 - 8 |
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Найти площадь поверхности, образованной вращением |
. |
|
|
|
||||||
|
|
|
кардиоиды ρ = 2а (1+ cosϕ) вокруг полярной оси. |
|
|
|
|
||||||
|
|
|
Решение: |
|
|
|
antigtu |
|
|
|
|
||
|
|
|
Имеем ρ′ = −2а sin ϕ, |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Qх =2ππ∫2a (1+cosϕ)sinϕ 4a cos ϕ dϕ = |
|
|
|
|
||||||
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
= 64 πа2 |
π∫cos4 ϕ sin ϕ dϕ |
= 128 |
πa2 . |
|
|
|
|
|
||
|
|
|
|
0 |
2 |
2 |
5 |
|
|
|
|
|
|
8.3.1. Вычисление объемов по заданным площадям поперечных сечений
Пусть имеем некоторое тело Т. Предположим, что известна площадь любого сечения этого
тела плоскостью, перпендикулярной оси Ох. |
||||||||
Эта площадь зависит от положения секущей |
||||||||
плоскости, то есть является функцией х: S =S(x). |
||||||||
Пусть S (x) непрерывна на [a, b]. Разобьем [a, b] |
||||||||
точками деления a = x0 < x1 < x2 <... < xn = b ; через |
||||||||
|
Скачано |
|
|
|
|
|||
точки |
xi проведем сечения, перпендикулярные |
|||||||
оси Ох. Площади с |
тветствующихс |
поперечных |
||||||
сечений - S (xi ). |
|
|
|
|
|
|||
|
|
|
|
|
n |
|
|
|
|
Составим сумму: Vn = ∑S (ξi )+xi , ξi [xi−1, xi ], S (ξi )+xi - объем цилинд- |
|||||||
|
|
|
|
|
i=1 |
|
|
|
ра с площадью ос ова ия S |
(ξi ) и высотой +xi . |
|||||||
Пусть |
max+xi → 0 , |
тогда |
Vn →V |
(объем тела). С другой стороны, |
||||
Vn → ∫b S (x)dx (Vn - интегральная сумма для непрерывной функции S (x)). |
||||||||
|
a |
|
|
|
|
|
|
|
Таким образом, V = ∫b S (x)dx . |
|
|
||||||
|
Пример: |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Найти объём тела, основание которого - круг радиусом а, а сечение |
|
||||
|
|
|
плоскостью, перпендикулярной фиксированному диаметру круга, есть |
|||||
|
|
|
равнобедренный треугольник высотой h. |
|||||
|
|
|
Решение: |
|
|
|
|
|
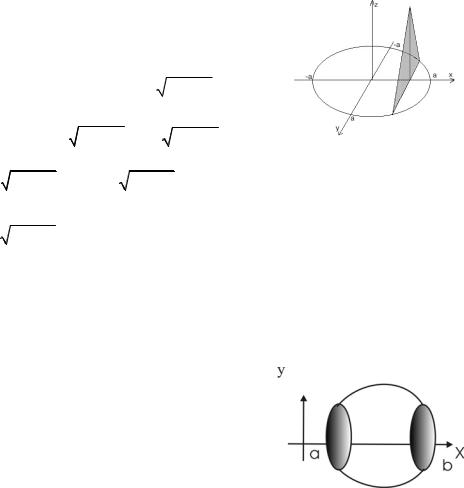
|
|
|
|
|
|
имеем S(х) = 12 2 |
a2 − x2 h = h a2 − x2 |
, |
|
. |
ru |
267 |
||||||||||||||||
|
Определенный интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
Выберем систему координат, начало кото- |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
рой совпадает с центром круга. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
Тогда сечение тела плоскостью, перпенди- |
|
|
|
|
|
|||||||||||||||||
|
x |
|
∫ |
|
кулярной оси Ох, есть равнобедренный тре- |
|
|
|
|
|
||||||||||||||||||
|
|
|
{ |
|
|
|
|
|
|
|
} |
|
∫ |
|
|
|
antigtu |
|
|
|
|
|||||||
|
|
|
|
|
|
угольник с основанием 2у = 2 |
a2 − x2 |
и вы- |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
сотой h; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
V = h ∫a |
a2 − x2 dx = 2h∫a |
|
a2 − x2 dx = |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
−a |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
2 |
|
2 |
|
a2 |
|
|
|
x |
a |
|
πa2h |
|
|
|
|
|
|
||
|
|
|
|
|
|
= 2h |
|
a |
|
− x |
|
+ |
|
arcsin |
|
|
|
|
= |
2 |
. |
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
a |
0 |
|
|
|
|
|
|
|
|||
|
8.3.2. Вычисление объемов тел вращения |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
Если криволинейная трапеция, ограниченная |
|
|
|
|
|
||||||||||||||||||||
|
кривой у = |
f (x), а ≤ х ≤ b, вращается вокруг оси |
|
|
|
|
|
|||||||||||||||||||||
|
Ох, то объём тела вращения вычисляется по фор- |
|
|
|
|
|
||||||||||||||||||||||
|
муле: |
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
V = b S (x)dx = S (x)= π f 2 (x) =π b |
f 2 (x)dx . |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Если криволинейная трапеция, ограниченная |
|
|
|
|
|
||||||||||||||||||||
|
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
кривой x = |
f (y), c |
≤ y |
≤ d, вращается вокруг оси Оу, то Vy =π ∫d |
f 2 (y)dy . |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
Если криволинейный сектор, |
|
граниченный кривой ρ = ρ(ϕ) |
и лучами |
||||||||||||||||||||||
|
ϕ =α и ϕ = β , вращается вокруг полярной оси, то V = 2 |
β |
|
|
|
|
||||||||||||||||||||||
|
π ∫ρ3 sinϕdϕ . |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
α |
|
|
|
|
|
! |
|
Величина Vу может быть также вычислена интегрированием по х: Vу = |
|||||||||||||||||||||||||
|
|
|
2π ∫b x |
f (x) |
dx , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Н йти объем тела, образованного вращением вокруг оси Ох фигуры, ог- |
|
|||||||||||||||||||||
|
|
|
|
|
|
р ниченной кривой у2 = (х − 1)3 и прямой х = 2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
1 π . |
|
|
|
|
|
|
||||
|
|
|
|
|
|
Vх = π ∫y2dx = π ∫(x −1)3 dx = |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
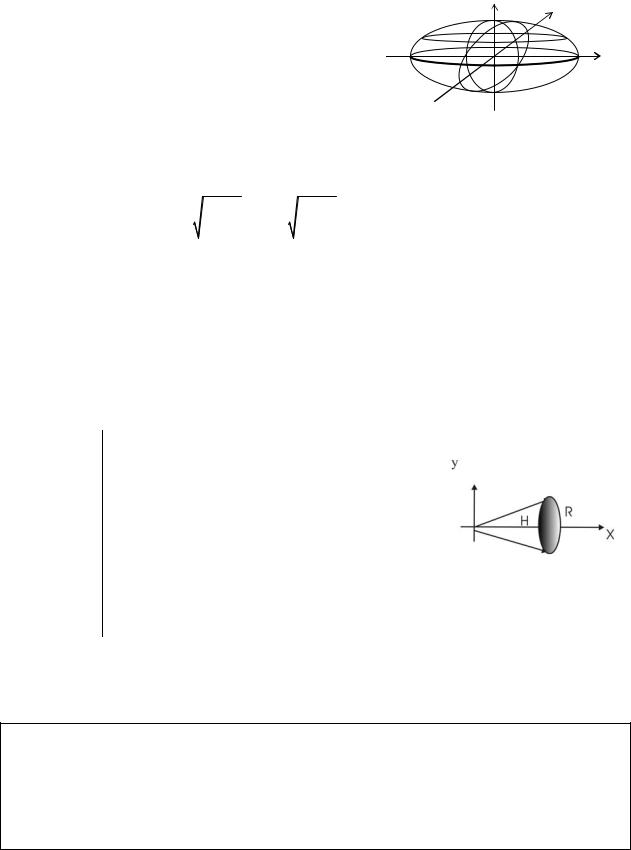
268 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
Лекции 7 - 8 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||
|
|
|
Найти объем тела эллипсоида |
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
+ |
y |
2 |
|
+ |
z |
2 |
=1. |
|
|
|
|
|
antigtu |
|
|
y |
|||||||||||||||||||||||
|
|
|
Решение: |
a2 |
|
|
|
b2 |
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
V = 2∫S |
(x)dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
дляфиксированного x имеемэллипс |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
y2 |
+ |
|
|
=1− |
|
|
или |
|
|
|
+ |
|
=1, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
b12 |
|
c12 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
b2 |
|
|
c2 |
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
= |
|
|
|
|
|
|||||
|
|
|
гдеb1 = b |
|
|
1− |
|
, c1 = c |
|
1− |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
a |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
S (x)=πb c =πbc |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
a |
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
a |
4 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
= 2πbc |
|
|
1 |
− |
|
|
|
|
dx = 2πbc |
x |
− |
|
|
|
|
|
|
|
|
|
0 = |
|
πabc , |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
∫0 |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3a |
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||||||||
|
|
|
V |
= 4 πabc , |
|
V |
|
|
= 4 πR3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
эл |
3 |
|
|
|
|
|
|
|
|
|
|
|
сф |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти объем кону а |
|
|
|
вы отой Н и радиусом |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
основания R. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
y = |
R |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
H R2 |
|
|
2 |
|
|
|
|
|
|
π R2 |
|
|
x3 |
|
H |
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Vx =π ∫0 |
H 2 |
x |
dx = |
|
H 2 |
|
3 |
|
0 |
|
= |
3 |
π R |
H |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
V |
= 1 π R2 H . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
кон |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В результате изучения материала, изложенного в этих лекциях, студенты должны знать:
формулу Ньютона-Лейбница;особенности применения основных методов интегрирования при вычисле-
нии определенных интегралов;геометрические приложения определенного интеграла.

Лекция 9 |
. |
ru |
|
||
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ |
|
|
|
|
При введении понятия определенного интеграла предполагалось, что отрезок [a,b] – конечный, а функция f(x) ограничена на этом отрезке. При нарушении хотя бы одного из этих условий вводят обобщение определенного интеграла – несобственные интегралы.
9.1. Несобственные интегралы первого рода (по бесконечному промежутку).
9.1.1. Основные определения 9.1.2. Обобщенная формула Ньютона-Лейбница
9.1.3. Признаки сходимости интегралов с бесконечными пределами 9.1.4. Абсолютная и условная сходимость
9.2. Несобственные интегралы второго рода (от неограниченных функций)
9.2.1. Признаки сходимости несобственных интегралов от неограниченных функций 9.2.2. Примеры решения задач
|
|
с |
9.1. Несобственные интегралы первогоantigtuрода |
||
(по бесконечному промежутку) |
||
Скачано |
|
|
9.1.1. Основные определения |
|
|
О Пусть функция f(x) непрерывна на интервале [a, ∞). Тогда она непрерыв- |
||
на на любом пр межутке |
[a,b], где b>a, и существует интеграл |
|
∫b |
f (x)dx . Несобстве ым и |
тегралом первого рода называется предел |
|
a |
|
|
|
|
|
|
|
|
|
|
|
limb→∞ ∫b |
f (x)dx |
|
и |
обозначается |
∞∫ f (x)dx . |
Таким |
образом, |
|||
|
a |
|
|
|
|
|
|
a |
|
|
|
|
∞∫ f ( x )dx = limb→∞ |
∫b |
f ( x )dx . |
|
|
|
|
||||
|
a |
|
|
a |
|
|
|
|
|
|
|
|
Если этот предел существует и конечен, то говорят, что несобственный |
||||||||||
О |
|||||||||||
интегр л сходится. Если же этот предел не существует или бесконечен, |
|||||||||||
|
|||||||||||
|
то говорят, что несобственный интеграл расходится. |
|
|||||||||
|
Аналогично определяется несобственный интеграл и для промежутка |
||||||||||
|
( −∞,b]: ∫b |
f ( x )dx = alim→−∞ ∫b |
f ( x )dx , если этот предел существует и коне- |
||||||||
|
|
−∞ |
|
|
|
a |
|
|
|
|
|
−∞ |
−∞ |
c |
ru |
|
270 |
|
|
|
Лекция 9 |
чен. Для функции f (x), непрерывной на промежутке ( −∞, +∞), несобствен-
где с – любое число. Несобственный интеграл в левой части.называется схо-
ный интеграл +∞∫ f (x)dx определяется равенством:
−∞ |
antigtu |
∫ |
|
+∞∫ f ( x )dx = ∫c |
f ( x )dx + +∞∫ f ( x )dx , |
дящимся, если сходится каждый несобственный интеграл в правой части.
9.1.2. Обобщенная формула Ньютона-Лейбница
Пусть F(x) – первообразная для функции f(x) на промежутке [a, ∞ ). Вос-
пользуемся формулой Ньютона-Лейбница для интеграла ∫b |
f ( x )dx . |
|
|||||||||||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
||
∞ |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
∫ |
f ( x)dx = lim |
∫ |
f ( x)dx = lim[ F(b)−F(a)] = lim F(b)−F(a). |
|
|||||||||||||||||||||||||||
|
|
|
|
b→+∞ |
|
|
|
|
|
|
b→+∞ |
|
|
|
|
|
|
|
b→+∞ |
|
|
|
|
|
|
||||||||
|
|
a |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если обозначить lim F( b ) через F(+ ∞ ), то можно записать: |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
b→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( x )dx = F( +∞ ) − F( a ) = F( x )|+∞ . |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
||
Аналогично |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
b |
|
|
|
|
|
|
|
|
|
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
f ( x )dx = F( x )|b−∞ , |
∫ |
f ( x )dx = F( x )|+∞−∞ , где F(- ∞ ) = lim F( x ) . |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
x→−∞ |
|
|
||||||||
|
−∞ |
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ dx |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Исследовать сходимость интеграла |
∫a |
x p |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
dx |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
При p ≠1 ∫ |
p |
= blim→+∞ ∫x− p dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
a |
|
x |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
x |
− p+1 |
b |
1 |
|
|
−p+1 |
|
1 |
|
|
−p+1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
= lim |
−p +1 |
|
|
|
|
= |
|
|
|
lim |
b |
− |
|
|
|
|
a . |
|
|
|
|
|
|
||||||
|
|
|
|
b→+∞ |
|
|
|
|
a |
|
−p+1b→∞ |
|
|
−p+1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Пусть р > 1, тогда −p +1 < 0 и |
|
|
− p+1 |
|
|
|
+∞ dx |
|
|
1 |
|
−p+1 |
|||||||||||||||||
|
|
|
|
lim b |
|
|
= 0, |
|
|
|
= − |
|
|
|
a |
, значит, |
|||||||||||||||||
|
|
|
|
|
|
∫a x p |
−p+1 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b→+∞ |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
при р > 1 интеграл сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
Пусть р < 1, тогда −p +1 > 0 |
и lim b− p+1 = ∞, т.е. интеграл |
+∞ dx |
при р < 1 |
||||||||||||||||||||||||||
|
|
|
|
∫a |
|
x p |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
||||

Несобственные интегралы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
271 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
При p =1: |
∞ dx |
= lim (lnx) |
|
b |
= lim (lnb −lna)= ∞ . Интеграл расходится. |
|||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∫a x p |
|
|
b→∞ |
|
|
|
a |
b→∞ |
|
|
|
ru |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Пример: |
|
. |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
Вычислить несобственные интегралы или доказать, что они |
расходятся: |
|
||||||||||||||||||||||||||
|
|
|
|
|
+∞ |
|
dx |
|
|
+∞ |
dx |
|
|
+∞ |
|
|
|
|
0 |
+∞ |
dx |
|
|
|
|
|
||||||
|
|
|
|
1) |
∫ |
|
; 2) |
∫ |
; 3) |
∫ cos xdx ; 4) ∫ exdx ; 5) |
∫ |
. |
|
|
|
|
||||||||||||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
1 |
|
x |
|
|
1 |
x |
|
|
|
0 |
|
|
|
|
−∞ |
−∞ |
1+ x |
|
|
|
|
||||||
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Воспользуемся обобщенной формулой Ньютона-Лейбница: |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
+∞ dx |
|
|
1 ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1) |
∫1 |
|
|
= − |
|
|1 |
|
= −( 0 |
−1) =1 (интеграл сходится). |
|
|
|
|
|||||||||||||||
|
|
|
|
|
x2 |
|
x |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
+∞ dx |
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2) |
∫1 |
|
|
|
= ln x | |
|
= lim ln x = ∞ (интеграл расходится). |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
1 |
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
3) |
∫ |
cosxdx = sinx |+∞ |
= lim sinx . Этот предел |
не существует, поэтому |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
x→+∞ |
=1−0antigtu=1 (интеграл сходится). |
|
|
|
|
||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
+∞∫ cosxdx - расходится. |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
4) |
∫ |
ex dx = ex |−∞0 |
= e0 − lim ex |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→−∞ |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
|
dx |
|
|
|
|
|
|
|
|
+∞ |
|
π |
|
|
|
π |
|
|
|
|
|
|
|
|||
|
|
|
|
5) |
−∞∫ |
|
|
= arctgx |−∞ |
= |
|
−( − 2 ) =π (интеграл сходится). |
|
|
|
|
|||||||||||||||||
|
|
|
|
1+ x2 |
2 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
||
|
Выясним геометрический смысл несобст- |
|
|
|
|
|
|
|
||||||||||||||||||||||||
венного интеграла 1-го рода. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Пусть |
|
f ( x ) ≥ 0 |
а промежутке [a,+ ∞). |
|
|
|
|
|
|
|
|||||||||||||||||||||
Тогда ∫b |
f ( x )dx |
численно р вен площади фи- |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гуры, ограни енной снизу отрезком [a,b] оси |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Ox, сверху – линией y = f |
|
(x), слева и справа – |
|
|
|
|
|
|
|
|||||||||||||||||||||||
прямыми x = a и x = b. При возрастании b |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
прям я x = b, огр ничивающая эту фигуру, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
двиг ется |
впр во, |
интеграл |
∫b |
f ( x )dx стре- |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Скачано |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
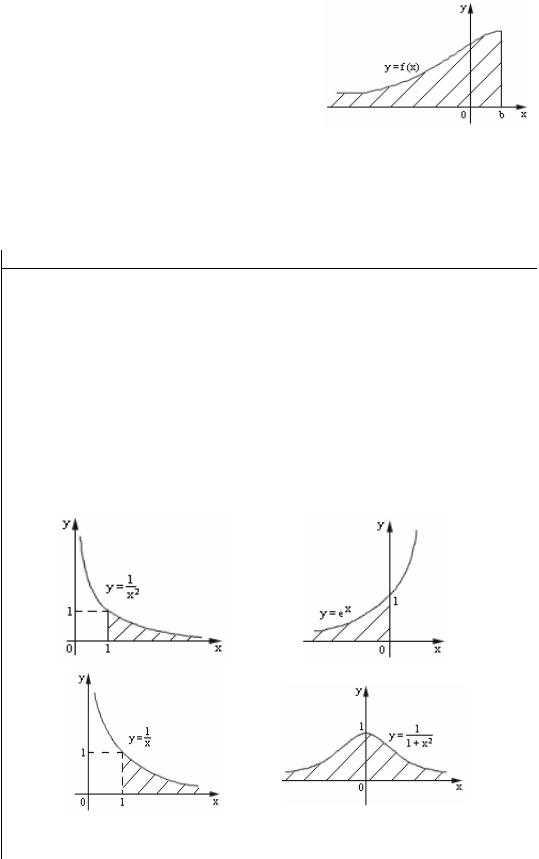
|
272 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекция 9 |
|
мится к интегралу ∞∫ f ( x )dx . Поэтому величи- |
. |
ru |
|
|||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
||
|
ну интеграла ∞∫ f ( x )dx |
|
|
естественно принять за |
|
||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
||
|
площадь бесконечной фигуры, ограниченной |
|
|||||||||||||
|
снизу |
осью Ох, сверху |
графиком функции |
|
|
||||||||||
|
y = f |
(x), слева – прямой x = a. |
|
|
|
|
|
||||||||
|
Аналогично ∫b |
f ( x )dx |
|
|
для случая f(x) ≥0 чис- |
|
|
|
|||||||
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
ленно равен площади бесконечной фигуры, ограниченной снизу осью Oх, |
||||||||||||||
|
сверху кривой y = f (x), справа прямой x=b. |
|
|
|
|||||||||||
|
Пример: |
Вычислить площади бесконечных фигур, ограниченных осью Ох, линией |
|||||||||||||
|
|
|
|||||||||||||
|
|
|
y = f(x), прямой x = a, если |
antigtu |
|
|
|
||||||||
|
|
|
а) f (x)= |
1 |
|
|
, a = 1, x ≥1; |
|
|
|
|||||
|
|
|
x2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
б) |
f (x)= |
1 |
|
|
, a=1, x ≥1; |
|
|
|
||||
|
|
|
x |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
в) |
f (x)= ex , a=0, x ≤ 0 |
; |
|
|
|
|||||||
|
|
|
г) f (x)= |
|
1 |
|
, x (−∞, +∞) . |
|
|
|
|||||
|
|
|
1+ x2 |
|
|
|
|
||||||||
|
|
|
Решение: |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Построим фигуры, ограниченные данными линиями |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Воспользуемся результатами примера 1. |
|
|
|
|||||||||
|
Скачано |
|
|
|
|
|
|
||||||||
|
Несобственные интегралы |
|
|
|
|
. |
ru |
273 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
+∞ |
|
|
|
|
|
|
|
|
|
а) S = ∫1 dxx2 =1; б) S = ∫1 dxx = ∞ ; |
|
|
|
|
||||
|
|
Фигура, изображенная на рис.б), имеет бесконечную площадь. |
|
|
|
|||||
|
|
0 |
+∞ |
dx |
|
antigtu |
|
|
|
|
|
|
в) S = ∫ ex dx =1; г) S = ∫ |
|
=π . |
|
|
|
|
||
|
1+ x |
2 |
|
|
|
|
||||
|
|
−∞ |
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9.1.3. Признаки сходимости интегралов с бесконечными пределами
Признаки сравнения
1. Пусть при а ≤ х < +∞, 0 ≤ f(х) ≥ g(х). Если +∞∫ g(x)dx сходится, то сходит-
|
|
|
a |
ся и +∞∫ f (x)dx , причем +∞∫ |
f (x)dx ≤ ∞∫g (x)dx . Если расходится +∞∫ f (x)dx , |
||
a |
a |
|
a |
то расходится и +∞∫ g (x)dx . |
с |
||
|
a |
|
|
|
|
|
|
2. Если при а ≤ х < +∞, f(х) > 0, g(х) > 0 и существует конечный предел
|
lim |
f (x) |
≠ 0 , то интегралы |
+∞ f (x)dx , |
+∞ g (x)dx сходятся или расходят- |
|||||||
|
|
|||||||||||
|
|
g (x) |
|
|
|
|
|
a |
a |
|||
|
Скачано |
|
|
∫ |
∫ |
|||||||
|
x→+∞ |
|
|
|
|
|
|
|
||||
|
ся одновременно. |
|
|
|
|
|
|
|
|
|
||
9.1.4. Абсолютная и усл вная сх димость |
|
|||||||||||
О |
Если сходится |
+∞∫ |
f (x) |
dx , |
|
то сходится и∞∫ f (x)dx . В этом случае |
||||||
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
∞∫ f (x)dx н зыв ется |
бсолютно сходящимся. |
||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
Если ∞∫ f (x)dx сходится, а +∞∫ |
|
f (x) |
|
dx расходится, то ∞∫ f (x)dx называется |
|||||||
О |
|
|
||||||||||
|
|
|
||||||||||
|
|
a |
|
|
|
a |
|
|
|
|
a |
|
условно сходящимся.
Из первого признака сравнения можно получить следующее утверждение.

. |
ru |
|
274 |
|
Лекция 9 |
Т |
Если при х → + ∞ функция f(х) > 0 является бесконечно малой порядка |
||||||
|
α по сравнению |
1 |
, то интеграл +∞∫ |
|
f (x) |
|
dx сходится при α > 1 и расхо- |
|
|
|
|||||
|
|
||||||
|
|
x |
|
|
|
|
|
|
Решение: |
a |
|||||
|
|
|
|
antigtu |
|||
|
дится при α ≤ 1. |
|
|
|
|
|
|
Признак сходимости Абеля
Пусть f(х) >0 и g(х) определены и ограничены при а ≤ х < +∞, причем
1) |
∞∫ f (x)dx сходится; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2) g(х) монотонна и ограничена, |
|
g( x ) |
|
≤k =co st . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Тогда сходится и интеграл ∞∫ f (x)g (x)dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислить +∞∫ e−3x dx . |
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Имеем |
+∞ |
e−3x dx |
= |
lim |
|
b |
e−3x dx = |
lim − |
1 e−3x |
|
b |
= 1 lim |
1−e−3b |
|
= 1 . |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
Скачано |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
0 |
3 |
b→+∞ |
( |
) |
3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
b→+∞ ∫ |
|
|
|
|
|
|
b→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
Несобственный интеграл сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
dxx2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Вычислить −∞∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
Реше ие: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
−1 |
dx |
|
|
|
−1 dx |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
∫ |
x |
2 |
|
= |
alim→−∞ ∫ |
|
x |
2 |
|
= alim→−∞ − |
|
|
|
|
= |
|
alim→−∞ |
1 |
+ |
|
|
|
|
|
= 1, т.е. предел существу- |
|||||||||||||||||||
|
|
|
|
−∞ |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
ет. Следов тельно, искомый несобственный интеграл сходится. |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Исследовать на сходимость интеграл |
∫2 |
|
|
|
|
|
. |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
x ln2 x |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
∞ |
dx |
|
|
|
|
b |
|
|
dx |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
∫ |
|
|
= blim→∞ |
|
∫ |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= blim→∞ |
|
|
|
|
|
|
= |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 x ln |
|
x |
|
|
|
2 |
x ln |
|
x |
|
|
|
|
|
|
|
ln x |
|
|
2 |
|
|
|
ln 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
т.е. несобственный интеграл сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
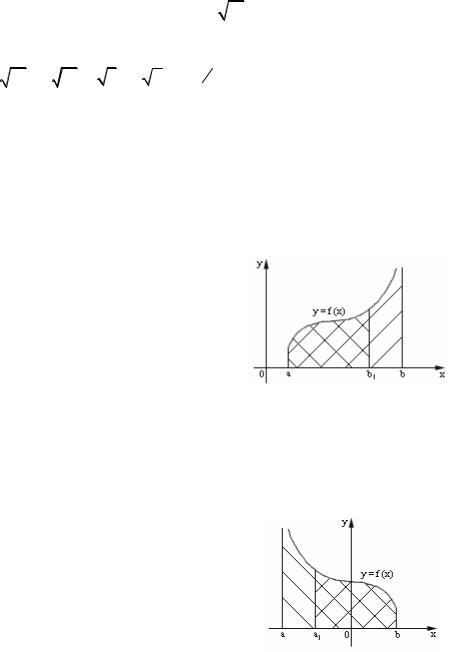
|
Несобственные интегралы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
275 |
||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
Исследовать на сходимость интеграл +∞∫ (x +31)dx . |
. |
|
|
|
|
|||||||||||||||
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x +1 |
|
|
|
|
|
∞ |
|
|
∞ |
|
|
|
|
|
|
|||||
|
|
|
|
x |
|
|
1 |
|
dx |
|
|
|
|
|
|
||||||||
|
|
|
Имеем: ( |
|
|
3 ) ≥ |
|
= |
|
, ∫ |
|
= ∫ |
dx |
расходится (здесь р = 1 |
< 1). |
|
|
||||||
|
|
|
3 |
|
|
|
|
|
1 |
|
|
||||||||||||
|
|
|
|
|
x |
|
x |
|
|
x |
a |
x |
antigtu |
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
a x 2 |
|
|
|
|
|
||||||||||
|
|
|
Следовательно, по признаку сравнения расходится и исходный интегралru |
. |
|
||||||||||||||||||
|
9.2. Несобственные интегралы второго рода |
|
|
|
|
|
|||||||||||||||||
|
|
(от неограниченных функций) |
|
|
|
|
|
|
|
|
|||||||||||||
|
О |
Пусть функция |
|
f (x) |
непрерывна на ин- |
|
|
|
|
|
|
||||||||||||
|
|
тервале [a,b) и неограниченна вблизи b. |
|
|
|
|
|
|
|||||||||||||||
|
|
Тогда функция непрерывна на любом от- |
|
|
|
|
|
|
|||||||||||||||
|
|
резке [a,b1], где а≤ b1<b и, следовательно, |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
существует интеграл ∫ f (x)dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
a |
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим blim→b−0 ∫ f (x)dx . Этот предел называется несобственным ин- |
|||||||||||||||||||||
1 |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тегралом второго рода и обозначается |
|
|
|
|
|
||||||||||||||||
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
∫b f (x)dx . Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
∫ f (x)dx = bli→mb−0 |
∫ f (x)dx . |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
a |
|
|
1 |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Если этот предел существует и конечен, то |
|
|
|
|
|
||||||||||||||||
|
|
несобственный и |
теграл |
|
азывается |
сходя- |
|
|
|
|
|
||||||||||||
щимся, в противном случае несобственный интеграл н зыв ется р сходящимся.
Аналоги но для функции f(x), непрерывной на промежутке (a,b] и неог-
рани енной вблизи а, несобственный интеграл ∫b |
f (x)dx определяется |
||
следующим обр зом: |
|
a |
|
|
|
|
|
b |
|
b |
|
∫ f ( x)dx = a lim→a+0 ∫ f ( x)dx . |
|
||
a |
1 |
a1 |
|
|
|
||
Если этот правосторонний предел существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходя-
щимся.
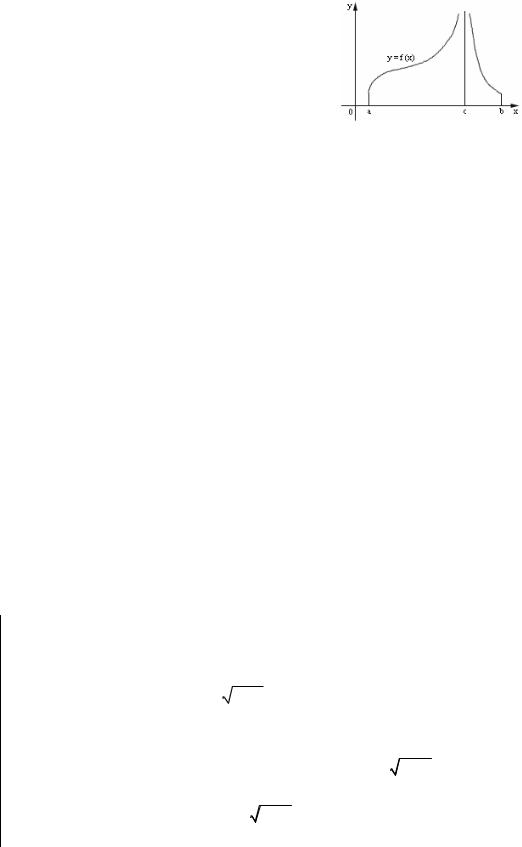
276 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекция 9 |
||
|
Пусть теперь функция |
f (x) |
непрерывна на отрезке [a,b] всюду, кроме |
|||||||||||||||||||||
|
некоторой точки c (a<c<b), и неограниченна |
|
. |
ru |
|
|
||||||||||||||||||
|
вблизи с. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Несобственный интеграл ∫b |
f (x)dx |
определя- |
|
|
|
||||||||||||||||||
|
ется равенством: |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
∫b |
f (x)dx = ∫c |
f (x)dx + ∫b |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
f (x)dx . |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
a |
|
|
a |
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если каждый из интегралов в правой части равенства сходится, то не- |
|||||||||||||||||||||||
|
собственный интеграл |
∫b |
f (x)dx |
называется сходящимся, |
в противном |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
случае – |
расходящимся. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Пусть F |
(x) |
– первообразная для функции |
f (x) на промежутке [a,b) и |
||||||||||||||||||||
|
f (x) |
не ограничена вблизи b. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
b |
|
|
|
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
∫ |
f (x)dx = lim |
f (x)dx = lim [F (b1 ) − F (a)] = lim |
|
F (b1 ) − F (a) . |
||||||||||||||||||
|
|
|
|
|
b1→b−0 ∫ |
|
|
|
b1 |
→b−0 |
|
|
|
b1→b−0 |
|
|
|
|||||||
|
|
|
a |
|
|
|
|
a |
F(b1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если обозначить |
lim |
через F(b), |
|
то получим следующий аналог |
|||||||||||||||||||
|
|
|
|
|
|
|
b1 |
→b−0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
формулы Ньютона-Лейбница для несобственного интеграла второго ро- |
|||||||||||||||||||||||
|
да: |
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
f (x)dx = F (b) − F (a) = F (x) |b , где F(b)= lim F (x) . |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
x→b |
−0 |
|
|
|
|
|
|
||
|
a |
|
|
|
|
|
|
|
|
с |
f (x), |
|
|
|
|
|
|
|
|
|
||||
|
Аналогично |
для |
|
|
не |
ограниченной |
|
вблизи а, |
||||||||||||||||
|
функции |
|
||||||||||||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
f (x)dx = F (x) |b |
, где F (a) = lim |
F ( x) . |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
a |
|
|
|
|
x→a + |
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислить несобственные интегралы или доказать, что они расходятся: |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1) ∫2 |
dx |
|
; 2) |
∫1 |
dx . |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 − x |
−1 |
x |
|
|
|
|
|
|||
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
В первом интеграле подынтегральная функция f (x)= |
|
не ограни- |
|||||||||||||||||
|
|
|
|
|
|
2 − x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
чена при x=2, поэтому интеграл ∫2 |
|
dx |
является несобственным. При- |
||||||||||||||||
|
|
|
|
|
|
2 − x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
меним обобщенную формулу Ньютона-Лейбница: |
|
|
|
|
|
||||||||||||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

Несобственные интегралы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
277 |
|||||
|
|
|
|
2 |
|
dx |
|
2 |
d (2 − x) |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
∫ |
|
|
= −∫ |
|
|
|
|
= −2 2 − x |0 |
= −(0 −2 2) = 2 2 . |
|
|
||||||||||||||||
|
|
|
|
|
2 − x |
|
2 − x |
|
|
||||||||||||||||||||||
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Во втором интеграле подынтегральная функция f(x)= |
1 |
не ограничена |
||||||||||||||||||||||||||
|
|
|
x |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
dx |
0 |
dx 1 dx |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вблизи x=0. Поэтому, по определению, −∫1 |
x |
= −∫1 |
x + ∫0 x . . |
|
||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
Рассмотрим интеграл |
∫0 |
dx = ln |
|
x |
|
0−1 = ∞ . |
Этот интеграл расходится, по- |
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
−1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
этому и интеграл ∫1 |
dx |
- расходится. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
−1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отметим, что если бы мы стали вычислять данный интеграл, не обращая |
||||||||||||||||||||||||||||
|
|
|
внимания на разрыв подынтегральной функции в точке x = 0, то получи- |
||||||||||||||||||||||||||||
|
|
|
ли бы неверный результат ∫1 |
dx |
= ln |
|
x |
|
1−1 = 0 , что неверно. |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
−1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Рассмотрим геометрический смысл несобственного интеграла 2-го рода. |
||||||||||||||||||||||||||||||
Пусть |
f (x) |
≥ 0 и f (x) |
– непрерывна на [ ,b) и не ограничена вблизи b. То- |
||||||||||||||||||||||||||||
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гда ∫ f (x)dx |
(b1 < b) равен площади фигуры, ограниченной снизу отрезком |
||||||||||||||||||||||||||||||
|
a |
|
|
|
|
|
|
y = f (x), |
|
|
|
|
antigtu |
|
|
|
|
|
|||||||||||||
[a,b1] оси Ох, сверху – линией |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
лева и справа – прямыми x=a, x=b1. |
|||||||||||||||||||||||||||||
При стремлении b1 к b, прямая x=b1 |
cтремится к прямой x=b. Поэтому |
||||||||||||||||||||||||||||||
|
b |
f (x)dx = ∫b |
|
|
естественноспринять за площадь бесконечной фигу- |
||||||||||||||||||||||||||
blim→b−0 ∫1 |
f (x)dx |
||||||||||||||||||||||||||||||
1 |
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
трезк м [a,b] оси Ох, сверху линией y = f (x), слева |
|||||||||||||||||||||||||||
ры, ограниченной снизу |
|||||||||||||||||||||||||||||||
и справа – прямыми x = a и x = b. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
9.2.1. Признаки сходимости |
|
есобственных интегралов |
|
|
|
|
|
||||||||||||||||||||||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
от неогр ниченных функций
Признаки сходимости и расходимости несобственных интегралов от неограниченных функций аналогичны признакам сходимости интегралов с бес-
конечными пределами. Эталоном сравнения служит интеграл
b |
dx |
|
|
∫ |
|
, (β > 0), |
|
(b −x) |
β |
||
a |
|
|
который сходится при β < 1 и расходится при β ≥ 1.
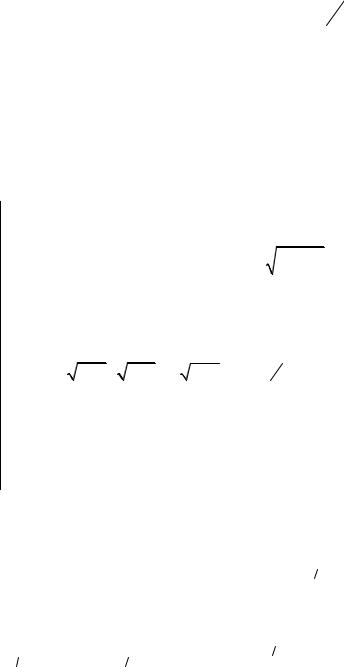
278 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
ru |
Лекция 9 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Исследовать на сходимость интеграл ∫ |
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
ln x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Решение: |
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
antigtu |
|
|
|
|
||||||||||||||||||||||||
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
При х |
→ 1 |
ln x |
|
(x |
−1) |
|
- эквивалентные бесконечные большие, т.к. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||
|
|
|
lim |
ln x |
= lim |
|
|
|
|
) |
|
= |
|
правилу |
|
= lim |
|
|
= 1, интеграл |
|
|
|||||||||||||||||||||||||
|
|
|
x→1 1 |
|
|
|
x→1 ln x |
|
|
|
|
|
|
|
|
|
|
x |
→1 |
( |
1 |
x) |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лопиталя |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β =1. Следовательно, |
2 |
dx |
|
|
|
|
|||||||||||||||||
|
|
|
∫ |
(x −1) |
расходится при |
∫ |
ln x |
расходится. |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
9.2.2. Примеры решения задач |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Исследовать сходимость интеграла ∫1 |
|
cos2 x |
|
dx . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
( |
|
− x2 |
) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Подынтегральная функция неограниченно возрастает при х → 1, пред- |
|||||||||||||||||||||||||||||||||||||||||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
ставим подынтегральную функцию в виде |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
f (x) |
= |
cos2 x |
|
|
1 |
|
|
= |
cos2 x |
|
1 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
3 1+ x |
|
3 1− x |
с |
3 1+ x |
(1− x)13 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
Первый с мн житель |
с бенности при х → 1 |
|
не даёт, а следовательно, |
||||||||||||||||||||||||||||||||||||||||
|
|
|
срав е |
ие с |
|
1 |
|
при х → 1 даёт α = |
13 |
< 1. Следовательно, интеграл |
||||||||||||||||||||||||||||||||||||
|
|
|
(x |
−1) |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вы ислить (или установить расходимость) |
+∞∫ cos xdx . |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
По определению, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
+∞ |
cos xdx = lim |
|
B |
cos xdx = lim |
|
sin x |
|
B |
|
|
|
= lim (sin B −1) = −1+ lim sin B . |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
∫ |
|
|
|
|
|
|
B→+∞ ∫ |
|
|
|
|
|
|
|
B→+∞ |
( |
|
|
|
π 2 ) |
|
B→+∞ |
|
|
|
|
|
B→+∞ |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
π 2 |
|
|
|
|
|
|
|
|
|
|
π 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Так как |
|
lim sin B не существует, то исследуемый несобственный инте- |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
B→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
грал расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Несобственные интегралы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
279 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Исследовать на сходимость |
|
∫3 |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
x3 + 2x + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
; f (х) = |
|
|
antigtu= , так как для любых х |
||||||||||||||||||||||||||||||||||||||
|
|
|
Здесь |
f (x) = |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
Рассмотрим f (x) = |
|
|
|
|
|
1 |
|
|
|
|
|
|
. Наибольшая степень многочлена в зна- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
x3 + 2x + 2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
менателе равна 3. Поэтому для сравнения |
возьмем функцию. |
g (х) = |
1 |
, |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3 |
||||
|
|
|
тогда |
|
lim |
|
|
|
|
= |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
= 1 ≠ 0 и по предельному признаку |
||||||||||||||||||||||||||||
|
|
|
|
x→∞ g (x) |
|
|
|
x→+∞ x3 + 2x + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
сравнения исследуемый несобственный интеграл и интеграл +∞∫ g (x) |
dx = |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫3 dxx3 сходятся или расходятся одновременно. Последний интеграл схо- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
дится (р > 1), следовательно, исследуемый интеграл тоже сходится. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Исследовать на абсолютную сходимость интеграл |
|
+∞ cos 2xdx |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∫ |
1+ x |
2 . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 2x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
cos 2x |
|
|
|
|
|
|
|
|
|
|
|
|
cos 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
1+ x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ x2 |
|
|
|
1+ x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Скачано |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= g(х). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
сos 2х ≤ 1, то f (х) ≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
1+ x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
Рассмотрим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
+∞ g (x)dx = +∞ |
|
|
dx |
|
|
|
= lim |
|
|
arctg x |
|
b |
= lim arctg b − lim arctg1= |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
1+ x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
1 |
|
1 |
|
2 |
|
|
b→+∞ ( |
|
|
|
|
1 ) |
|
|
b→+∞ |
|
|
|
|
|
|
|
b→+∞ |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
∫ |
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
= π − |
π |
= π , следовательно, |
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
∫ g (x)dx сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
2 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
(x) |
|
|
|
|
|
|
|
|||||
|
|
|
Тогда по призн ку сравнения сходится интеграл |
∫ |
|
f |
|
dx , а исследуе- |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
мый интеграл сходится абсолютно. |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Вычислить (или установить расходимость) |
∫1 |
|
dx |
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
1− x |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Функция f (x) |
= |
|
|
|
|
|
|
|
непрерывна для х [0, 1) и |
lim f (x)= +∞ . |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
− x2 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→1−0 |
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
dx |
|
|
|
|
|
|
|
|
|
1−ε |
|
dx |
|
|
= εlim→+0 (arcsin |
|
|
10−ε )= |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
Тогда ∫ |
|
|
= εlim→+0 |
∫ |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
1− x |
|
|
|
|
|
|
|
|
|
0 |
|
|
1− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
280 |
|
|
|
|
|
ru |
Лекция 9 |
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
= lim arcsin (1−ε ) −arcsin 0 = |
π |
− 0 = π , т.е. интеграл сходится. |
|
|
|
|||
|
|
ε→+0 |
|
2 |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|
В результате изучения материала, изложенного в этих лекциях, |
|
|
|
|
|||||
|
студент должен знать: |
|
|
|
|
|
|
|
||
|
|
понятие несобственного интеграла первого и второго рода, |
|
|
|
|||||
|
|
признаки сходимости несобственных интегралов. |
|
|
|
|
|
|||
|
Студент должен уметь: |
|
|
|
|
|
|
|
||
|
|
исследовать несобственные интегралы на сходимость. |
|
|
|
|
||||
|
Скачано |
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

Лекции 10 - 11 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дифференциальные уравнения, содержащие неизвестную функцию, ее производные
и известные функции независимого аргумента, начали исследоваться одновременно с воз- |
|
. |
ru |
никновением дифференциального и интегрального исчислений. Важность таких уравнений обусловлена тем, что в очень большом количестве случаев законы природы, управляющие теми или иными процессами, выражаются в форме дифференциальных уравнений, а расчет течения этих процессов сводится к решению дифференциального уравнения.
10.1. Основные понятия
10.2. Дифференциальные уравнения первого порядка (ДУ-I) 10.2.1. ДУ с разделяющимися переменными 10.2.2. Однородные ДУ первого порядка
10.2.3. Обобщенные однородные ДУ первого порядка 10.2.4. Линейные ДУ первого порядка 10.2.5. Уравнение Бернулли 10.2.6. Уравнение в полных дифференциалах
10.2.7. Таблица 1. Решения ДУ первого порядка 10.2.8. Особые решения ДУ первого порядка
11.1. ДУ высших порядков |
|
|
|||||
|
|
|
|
|
с |
|
|
11.2. ДУ второго порядка (ДУ-II) |
|||||||
11.3. Некоторые типы ДУ второго порядка, |
|||||||
приводимые к ДУ первого порядкаantigtu |
|||||||
11.3.1. ДУ y′′ = f ( x) |
|
|
|
||||
Скачано |
′′ |
|
|
|
′ |
||
11.3.2. ДУ вида y |
|
= f (x, y ) |
|||||
11.3.3. ДУ y |
′′ |
= f |
|
|
′ |
) |
|
|
(y, y |
|
|||||
11.4. Таблица 2. Решения ДУ второго порядка, допускающих понижение п рядка
11.5. ДУ n - го п рядка, д пускающие понижение порядка
11.5.1. ДУ вида y(n) = f ( x)
11.5.2. ДУ вида F (y, y ', y ",..., y(n) )= 0 11.5.3. ДУ вида F (x, y(k ),..., y(n) )= 0 .
11.5.4. ДУ вида dxd G (x, y, y ',..., y(n−1) (x))= 0 .
10.1. Основные понятия
О Дифференциальным уравнением (ДУ) называется уравнение, связы-
вающее между собой независимую переменную х, искомую функцию y = f (x) и ее производные y′, y′′,...y

282 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекции 10 - 11 |
||||
|
Например, скорость тела v , движущегося под действием силы F, |
|
может быть |
|||||||||||||||||||||||
|
найдена из второго закона Ньютона, т.е. из ДУ |
m dv |
= F , где m - |
масса тела, |
||||||||||||||||||||||
|
t - время. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
ДУ с одной независимой переменной называется обыкновенным. |
|||||||||||||||||||||||
|
|
|
Порядок наивысшей производной, |
|
входящей в уравнение, |
ru |
называется |
|||||||||||||||||||
|
О |
|
|
|||||||||||||||||||||||
|
|
|
порядком ДУ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Общий вид ДУ n-го порядка: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2 |
|
F( x, y, y′, y′′,...y( n ) ) = 0 . |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Например, 1. |
y′+ x y = sinx , 2. |
y′′′+ yy′ = 0 . |
|
|
|
|
|
|
|||||||||||||||
|
|
|
Решением или интегралом ДУ называется всякая функция y = f ( x ) , |
|||||||||||||||||||||||
|
|
|
которая, будучи подставлена в ДУ, превращает его в тождество. |
|||||||||||||||||||||||
|
|
|
График решения называется интегральной кривой. |
|
|
|
|
|||||||||||||||||||
|
|
|
Основная задача интегрального исчисления заключается в нахождении |
|||||||||||||||||||||||
|
|
|
решения ДУ y′ = f ( x ) , т.е. |
y = ∫ f ( x )dx + c . |
|
|
|
|
|
|||||||||||||||||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Найдите решение ДУ y′′ = 0 . |
antigtu |
|
|
|
|
||||||||||||||||
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
′′ |
|
′ ′ |
|
|
′ |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
y |
|
|
→ y |
= c1 |
, y = |
∫c1dx + c2 = c1 x + c2 . |
|
|
|
|
|||||||||||
|
|
|
|
|
|
= ( y ) = 0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
,..., y |
( n ) |
) |
= |
0 называется такое решение |
|||||||
|
О |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Общим решением ДУ F( x, y, y |
|
|
|||||||||||||||||||||
|
|
|
y = f ( x,c1 ,c2 ,...,cn ) , |
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
к т р е с держит столько независимых произволь- |
|||||||||||||||||||||||
|
|
|
ных постоянных ci , |
i =1,2,...n , каков порядок этого ДУ. |
|
|
|
|
||||||||||||||||||
|
|
|
Если общее реше ие задано в неявном виде Φ( x,y,c1 ,c2 ,...,cn ) = 0 , оно |
|||||||||||||||||||||||
|
О |
|
||||||||||||||||||||||||
|
|
|
называется общим интегралом ДУ. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Всякое решение ДУ, |
которое получается из общего при определенных |
||||||||||||||||||||||
|
О |
|
||||||||||||||||||||||||
|
|
|
зна ениях произвольных постоянных, называется частным решением |
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||
|
|
|
этого ДУ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н йдите решение ДУ y′′+ y = 0 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
Решение: |
′′ |
|
|
|
|
|
′′ |
= −cosx , |
функция вида y = c1sinx +c2cosx ; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
Так как (sinx) |
= −sinx , (cosx) |
||||||||||||||||||||
|
|
|
|
|
будет удовлетворять уравнению. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
Если |
c1 = 2 , |
|
c2 = 5 , |
то |
y1 = 2sinx +5cosx ; |
если c1 = 0 , |
|
c2 = −4 , то |
|||||||||||||
|
|
|
|
|
y2 |
= −4cosx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
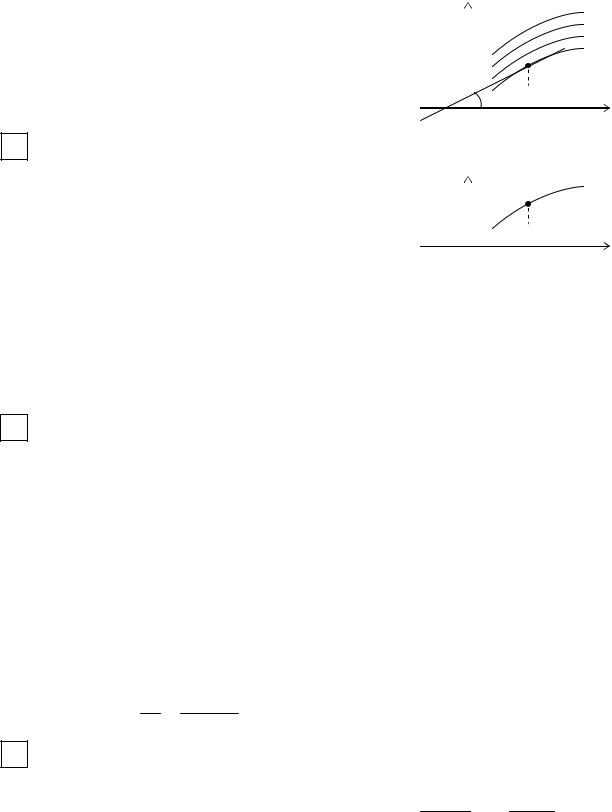
Дифференциальные уравнения |
|
|
|
|
|
|
|
283 |
|||
10.2. Дифференциальные уравнения первого порядка |
|
|
|
||||||||
|
Рассмотрим ДУ |
вида F( x, y, y′) = 0 |
или |
y |
|
|
С3 |
||||
y′ =ϕ( x, y ). |
Общим |
решением является |
|
|
|
С2 |
|||||
y = f ( x,c ) . Геометрически решение представ- |
|
|
|
С1 |
|||||||
|
|
|
С |
||||||||
ляет собой однопараметрическое семейство кри- |
α . |
Mru( x, y) |
|||||||||
вых. Значение y′ в точке M ( x, y ): y′ = tg α . |
|
x |
|
x |
|||||||
|
|
|
|
|
|
|
|
0 |
|
||
О |
Задача Коши для ДУ формулируется сле- |
|
|
|
|
||||||
|
дующим образом: найти решение y = f ( x ) |
y |
|
|
|
||||||
|
ДУ y′ =ϕ( x, y ), |
удовлетворяющее началь- |
|
|
|
||||||
|
|
|
|
|
|||||||
|
ному условию: y0 |
= f ( x0 ). |
|
|
|
M ( x0 , y0 ) |
|||||
|
|
|
|
y0 |
|
||||||
|
Геометрически задача Коши заключается в |
|
|
||||||||
|
0 |
x0 |
|
x |
|||||||
|
нахождении частного решения ДУ, прохо- |
|
|||||||||
|
|
|
|||||||||
|
дящего через заданную точку с координа- |
|
|
|
|
||||||
|
тами ( x0 ,y0 ) . |
|
|
|
|
|
|
|
|
|
|
|
Общее решение y = f ( x,c ) |
становится ча- |
|
|
|
|
|||||
|
стным |
y = f ( x,c0 ) , |
если |
y0 |
= f ( x0 ,c ) , |
от- |
|
|
|
|
|
|
куда можно найти c = c0 . |
|
с |
|
|
|
|
|
|||
|
уще твованияantigtuи единственности решения ДУ |
||||||||||
Т |
Теорема Коши (теорема |
||||||||||
|
первого порядка, разрешенного отно ительно производной). Если функ- |
||||||||||
|
Скачано |
|
|
|
|
,y0 ) , то су- |
|||||
|
ция ϕ( x, y ) непрерывна в обла ти, одержащей точку ( x0 |
||||||||||
|
ществует функция |
y = f ( x ) , удовлетворяющая уравнению |
y |
′ |
=ϕ( x, y ) |
||||||
|
и обращающаяся в y0 при x = x0 . |
|
|
|
|
|
|||||
|
Если, кроме того, непрерывна и частная производная ϕ′y ( x,y ) , то реше- |
||||||||||
|
ние будет еди стве |
ым. |
|
|
|
|
|
|
|
||
10.2.1. ДУ с р зделяющимися переменными
ДУ y′ =ϕ( x, y ) удобно записать в виде:
dydx = Q(P( x,yx,y )) или P( x, y )dx −Q( x, y )dy = 0 .
О ДУ X ( x )Y ( y )dx + X1( x )Y1( y )dy = 0 называется ДУ с разделяющимися
переменными.
Разделим уравнение на Y ( y ) X1( x ) ≠ 0 , тогда X ( x ) dx + Y1( y ) dy = 0 .
X1( x ) Y ( y )
Обозначим входящие в это уравнение функции через P( x ) и Q( y ) , то-
гда получим ДУ P( x )dx + Q( y )dy = 0 с разделенными переменными.
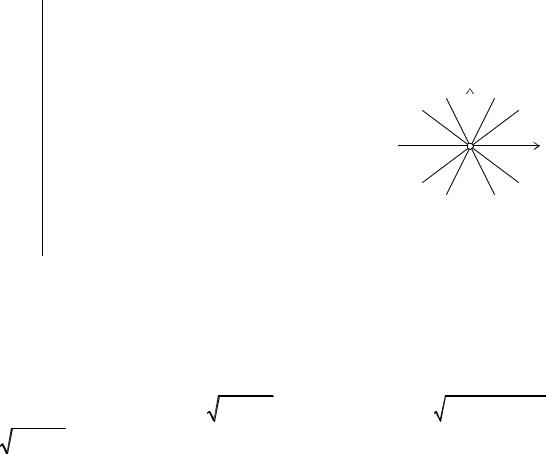
284 |
|
Лекции 10 - 11 |
. |
ru |
|
Считая y функцией x , перепишем уравнение в виде P( x )dx = −Q(y)dy , т.е.
в виде равенства дифференциалов двух функций одного аргумента. Известно, что если дифференциалы функций равны, то сами функции отличаются на
константу, т.е., общий интеграл этого ДУ имеет вид:
∫P( x )dx + ∫Q( y )dy = c .
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Найдите решение ДУ y′ = |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
dy y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
±y =| cx | |
|
|
|
C = 2 |
|
|
|
|
||||||||
|
|
|
|
|
|
dx |
= |
|
, xdy = ydx , умножая уравнение на |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
C = 1 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
, последовательно получаем |
|
dy = dx , |
|
|
|
|
|
0 |
|
|
|
|
|
|
x |
||||||||||||||||||||||||||
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
∫dy = |
∫dx |
, ln |
|
y |
|
= ln |
|
x |
|
+ln |
|
c |
|
, где постоянная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
y |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
интегрирования представлена в логарифмической форме, значит, |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ln | y |= ln | cx |, | y |=| cx |, x ≠ 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
10.2.2. Однородные ДУ первого порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
Функция F( x, y ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
О |
|
|
называет я однородной функцией n-го порядка, |
если |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
для любого числа k имеет место тождество F( kx,ky ) ≡ k n F( x, y ) . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
Например, |
если |
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
3 |
, |
то |
F( kx,ky ) = |
3 |
|
|
|
3 |
|
|
|
3 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ y |
|
( kx ) +( ky ) = |
|||||||||||||||||||||||||||||||||
|
|
|
F( x,y ) =сx |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
= k 3 |
x3 + y3 , значит, F( x, y ) является однородной функцией первого по- |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
рядка. Фу кция F( x, y ) = ex−y |
не является однородной. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
ДУ |
y′ = |
f ( x, y ) |
азывается |
однородным |
относительно х |
и у, |
|
если |
|||||||||||||||||||||||||||||||||||||
О |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
f ( x, y ) |
есть |
однородная |
|
|
функция |
|
|
нулевого порядка, |
|
то |
|
есть |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
f ( kx,ky ) = f ( x, y ). |
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
Решим однородное уравнение |
|
|
= f ( x,y ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
dx |
y |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Преобр зуем функцию f (x, y) к виду f (x, y) = f |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
1, |
|
, считая k = |
x |
. Решаем |
||||||||||||||||||||||||||||||||||||||||||||
x |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
dy |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u = |
|
y |
|
|
|
y = u x |
|
|
dy |
= u + |
du |
x |
|||||||||||
ДУ |
|
|
= |
f 1, |
|
. Сделаем подстановку |
|
|
, тогда |
, |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
dx |
|
|
x |
|
dx |
dx |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Дифференциальные уравнения |
285 |
и уравнение примет вид: u + x |
du |
= f (1,u ) - ДУ с разделяющимися перемен- |
||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
du |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
dx |
|
|
|
|
|
ru |
||||||
ными. x |
= f (1,u ) −u , |
|
du |
|
|
= |
|
dx |
|
, |
∫ |
|
= |
∫ |
|
+ c |
|
|||||||||||||||||||||||||||
|
|
f (1,u ) −u |
x |
f (1,u ) −u |
x |
|
||||||||||||||||||||||||||||||||||||||
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||||||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
Найдите решение ДУ y′ |
|
|
|
y |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
= |
|
|
ln |
|
|
+1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это ДУ является однородным, т.к. правая часть есть функция только от- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ношения |
y |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Положим |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
= u , y = ux , тогда y |
= u x +u и уравнение принимает вид: |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
′ |
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
du |
|
= |
dx |
|
|
|
|
|
|
|
|
|
|
+ln |
|
c |
|
, lnu = cx , |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
u x + u = u (lnu +1), u x =ulnu , ulnu |
x , ln |
|
lnu |
|
= ln |
|
x |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
откуда u = ecx , значит, |
y = xecx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
10.2.3. Обобщенные однородные ДУ первого порядка |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
a1 x + b1 y + c1 |
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|
||||||||||||||||||
|
ДУ вида |
y′ = f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
называется обобщенным однородным |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
a2 x + b2 y + c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
зованием параллельного переноса координат с помощью замены переменных
ДУ первого порядка и решается путем сведения к однородному ДУ преобра- |
|
Скачано |
с |
x = X +α, |
a α + b β + c = 0, |
||
|
при усл вии, что 1 |
1 |
1 |
y = Y + β , |
a2α + b2 β + c2 = 0. |
||
Проиллюстрируем реше ие обобщенных однородных ДУ первого по-
рядка на примере. Н йдем общий интеграл дифференциального уравнения
y′ = |
y + 2 |
|
|
. |
|
2x + y − 4 |
||
Сведение к однородному достигается преобразованием параллельного пере-
носа системы координат, |
x = X +α , y =Y + β . |
|
|||||||
При этом |
dy |
= |
d(Y + β ) |
= |
dY |
, и в новых переменных уравнение принимает |
|||
dx |
d( X +α ) |
dX |
|||||||
|
|
|
|
|
|||||
вид: |
|
|
|
dY |
|
Y +( β + 2 ) |
|
||
|
|
|
|
= |
. |
||||
|
|
|
|
|
2 X +Y +( 2α + β − 4 ) |
||||
|
|
|
|
dX |
|
||||

286 |
ru |
Лекции 10 - 11 |
|
||
Выбирая постоянные α и β из условия β + 2 = 0, |
|
|
2α + β − 4 = 0, |
|
|
получаем α = 3, β = −2 ; т.е. искомое преобразование переменных имеет вид:
|
|
|
|
|
|
x = X + 3 |
|
|
|
antigtu |
. |
|
||||||||||
|
|
|
|
|
|
, y = Y − |
2 |
, |
|
|||||||||||||
а уравнение упрощается |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
dY |
= |
|
|
|
Y |
|
|
|
|
. |
|
|
|
|
(1) |
|
|
|
|
|
|
|
dX |
|
|
2 X +Y |
|
|
|
|
|
|
|
||||||
Поделив числитель и знаменатель в правой части на Х (при X ≠ 0 ), получаем |
||||||||||||||||||||||
однородное уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
dY |
|
= |
|
|
Y X |
|
, при X ≠ 0 . |
|
(2) |
|||||
|
|
|
|
|
|
|
|
dX |
|
|
|
2 +Y X |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Используя подстановку Y |
X = u( x ), получаем |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
X |
|
du |
|
= |
|
−u2 −u |
. |
|
(3) |
|||||
|
|
|
|
|
|
|
|
dX |
|
|
2 + u |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Разделяя переменные, приходим к уравнению: |
|
|
|
|
||||||||||||||||||
Скачано |
|
|
dX |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 + u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
du = − |
с |
; ( u ≠ 0 , u ≠ −1, X ≠ 0 ). |
|
|
||||||||||||||
|
u2 + u |
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Интегрируя, находим общий интеграл в форме: |
|
|
|
|||||||||||||||||||
2 +u |
du = |
|
(1 +u )2 −u du 2ln | u | −ln |1+u | +ln | X |= C , |
|
||||||||||||||||||
∫u2 +u |
∫ |
|
|
u2 +u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
( u ≠ 0,u ≠ −1,X ≠ 0 ).
Слу ай X = 0 следует проверить подстановкой в уравнение (1), а случаи u = 0 и u = −1 - подстановкой в уравнение (3), поскольку возможна потеря решений. Находим, что X = 0 не является, а u = 0 и u = −1 являются решениями ур внения (1).
Т ким обр зом, уравнение (3) имеет следующие решения: |
|
2ln |u | −ln |1 + u | +ln | X |= C1 (общий интеграл), |
(4а) |
u = 0 , |
(4б) |

Дифференциальные уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
287 |
||
|
|
u = −1 (частные решения). |
|
|
|
|
|
|
|
ru |
(4в) |
||||||||||||||||||||
Возвращаясь к старым переменным, получаем: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
y + 2 |
|
|
− ln |
|
1 + |
y + 2 |
|
|
+ ln | x − |
3|= C , |
(5а) |
|||||||||||||||
|
|
|
2ln |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
x −3 |
|
|
|
|
|
|
|
x −3 |
|
|
|
|
|
|
|
1 |
. |
|
|||||||
|
|
|
|
|
|
|
y + 2 = 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5б) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
y + 2 |
|
= −1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5в) |
||||||
|
|
|
|
|
|
|
x −3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
После упрощения общий интеграл (5а) принимает вид: |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
2ln | y + 2 | −ln | x + y −1|= C . |
|
|
|
|
(6) |
||||||||||||||||||||||
Ответ: общий интеграл имеет вид: 2ln | y + 2 | −l | x + y −1|= C . |
|
|
|
|
|||||||||||||||||||||||||||
Замечание: общий интеграл (6) можно представить также в форме: |
|
||||||||||||||||||||||||||||||
ln |
|
( y + 2 )2 |
|
= C |
или |
|
( y + 2 )2 |
= C |
2 |
, C |
2 |
= ±eC1 . |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
x + y −1 |
1 |
|
|
|
|
|
x + y −1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Тогда частные решения (5б) и (5в) получаются при C2 = |
0 и C2 |
= ∞ соответ- |
|||||||||||||||||||||||||||||
ственно. |
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
10.2.4. Линейные ДУ перв го п рядка
О Линейным ДУ первого порядка называется уравнение, линейное отно- |
|
сительно |
еизвест ой функции y и ее производной y′: |
y′+ P( x )y = Q( x ), где P( x ), Q( x ) – непрерывные функции.
Ищем решение в виде произведения двух функций y = u( x ) υ( x ), одна
из которых счит ется произвольной (υ ), а другая находится из уравнения.
Если y = u υ , то |
|
′ |
|
|
|
′ |
′ |
|
|
dy |
|
|
dυ |
|
|
|
du |
|
|
||||
y |
= uυ |
, то есть dx = u dx + |
υ dx и уравнение прини- |
||||||||||||||||||||
|
|
+υu |
|||||||||||||||||||||
мает вид: |
dυ |
|
|
|
du |
|
|
dυ |
|
|
|
|
|
du |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
u |
|
+υ |
|
|
+ Puυ = Q , u |
|
|
+ Pυ +υ |
|
|
|
= Q . |
(*) |
||||||||||
|
dx |
|
|
|
dx |
|
|
dx |
|
|
|
|
dx |
|
|
|
|||||||
В силу произвольности выберем υ такой, что |
dυ |
+Pυ=0, тогда |
dυ |
= −Pdx , |
||||||
dx |
|
υ |
||||||||
|
|
|
|
|
|
|
||||
ln |
|
υ |
|
= −∫Pdx + lnc1 , значит υ = c1e−∫Pdx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||

. |
ru |
|
288 |
|
Лекции 10 - 11 |
Положим c1 =1, получим υ = e−∫Pdx . Подставляя полученное для υ выражение в ДУ (*), найдем u :
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
antigtu3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
υ( x ) |
dx |
= Q( x ) , |
|
dx |
|
= |
|
υ( x ) |
, |
|
u |
|
= ∫Q(x) dx |
+ c |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
В итоге общее решение имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y =υ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(x) |
∫ |
Q(x) dx + c . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Найдите решение ДУ |
dy |
− |
|
|
2 |
|
y = ( x +1)3 , x ≠ −1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
dx |
|
x +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Полагая y = uυ , получим, что dy |
|
|
= u |
dυ |
+ du υ , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
dυ |
|
du |
|
|
2 |
|
|
|
|
|
|
|
|
3 |
, |
|
dυ |
|
|
|
|
|
|
2 |
|
|
|
du |
|
|
|
|
|
|
3 |
. |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
u |
|
|
+ |
|
υ − |
|
|
uυ = ( x + |
1) |
|
|
u |
|
|
|
|
|
− |
|
|
|
|
|
υ |
+υ |
|
|
|
|
|
= ( x +1) |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
dx |
|
dx |
|
|
x +1 |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
x |
+1 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
Найдем υ из ДУ |
dυ |
− |
|
|
2 |
|
υ = 0 , |
|
dυ |
= |
2dx |
|
, ln |
|
υ |
|
= 2 ln |
|
x +1 |
|
, |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
x +1 |
|
|
|
|
|
|
|
|
|
|
υ |
|
|
|
|
|
x +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
откуда υ = ( x +1)2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
Найдем u из ДУ: ( x +1) |
|
du |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
|
|
|
|
(x +1)2 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
dx |
|
= ( x + |
1) |
, |
|
dx |
|
= ( x +1) , |
u = |
|
|
|
|
+ c . |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( x +1)4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
Общее решение примет вид: y = |
|
|
|
|
|
|
2 |
|
|
|
+ c(x +1)2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
10.2.5. Уравнение Бернулли |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
О |
|
ДУ |
dy + P(x) y = Q(x) yn , где |
P(x) , |
|
|
|
Q(x) |
|
– |
непрерывные функции или |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
dx |
|
|
|
азывается уравнением Бернулли. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
постоянные, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
При |
n = 0 |
оно линейное, при |
|
|
n =1 |
|
|
с разделяющимися переменными. |
||||||||||||||||||||||||||||||||||||||||||||||||||
Считаем, |
то n ≠ 0, 1. Разделим ДУ на yn , получим y−n dy |
|
+ Py−n+1 = Q . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
||
Сдел ем з мену переменной z = y−n+1 , |
|
тогда получим |
dz |
= (−n |
+1) y−n dy |
, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
dx |
|
|
|||||
|
+ (−n +1)Pz = (−n +1)Q - линейное уравнение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
dx |
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Найдите решение ДУ |
dy + xy = x3 y3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
Решение: |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

|
Дифференциальные уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
|
289 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Здесь P(x) = x , |
Q(x) = x3 , |
|
n = 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
−3 |
′ |
|
|
−2 |
|
|
|
3 |
|
|
|
|
|
|
|
|||||
|
|
|
Умножив уравнение на |
|
|
, получим y |
|
|
y |
+ xy |
|
|
|
= x |
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
y3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
Заменяя z = y−n+1 = y−2 , получаем dz |
= −2 y−3 dy |
, |
|
|
dz |
−2xz = −2x3 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
dx |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полагая |
z = uυ , |
|
|
|
dz |
= u dυ + du υ , |
|
|
|
|
|
|
dυ + du |
υ −2x υ = −2x3 , |
|||||||||||||||||||||||||
|
|
|
dυ |
|
|
|
du |
|
|
|
|
|
dx |
|
|
dx |
dx |
|
|
|
|
|
|
|
dx |
|
|
dx |
|
|
|
|
|
|
||||||||
|
|
|
u |
dx |
−2xυ |
+υ |
dx |
= −2x |
|
, |
|
приходим |
|
|
к |
|
|
линейному |
ДУ |
для |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
υ : |
dυ |
−2xυ = 0 , |
dυ |
= 2xdx , откуда ln |
υ |
= x2 ,υ = ex2 . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
dx |
|
|
|
υ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда уравнение для u принимает вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ex2 du |
= −2x3 , du = −2e−x2 x3dx , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
откуда u = −2∫e−x2 x3dx =(по частям)= = x2e−x2 +e−x2 +c , |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
z = uυ = x2 +1+ cex2 , y−2 = x2 +1+cex2 , y = |
|
|
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
x2 +1+cex2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Заметим |
, что уравнение Бернулли можно решить как линейное, сразу |
|||||||||||||||||||||||||||||||||||||||
|
сделав замену y = uυ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
10.2.6. Уравнение в полных дифференциалах*) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
Уравнение |
P(x, y)dx + Q(x, y)dy = 0 |
называется уравнением в полных |
||||||||||||||||||||||||||||||||||||||
|
О |
|||||||||||||||||||||||||||||||||||||||||
|
|
Скачано |
|
P(x, y) и Q(x, y) – непрерывные дифференци- |
||||||||||||||||||||||||||||||||||||||
|
|
дифференциалах, |
если |
|
||||||||||||||||||||||||||||||||||||||
|
|
руемые функции, для к т рыхс |
∂P |
= |
∂Q |
, причем |
∂P |
|
и |
|
∂Q |
непрерывны |
||||||||||||||||||||||||||||||
|
|
в некоторой области. |
|
|
|
|
|
|
|
|
|
|
∂y |
∂x |
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
∂x |
|
|
|
|
||||||||||
|
Т |
Для того чтобы выраже ие Pdx + Qdy |
было полным дифференциалом |
|||||||||||||||||||||||||||||||||||||||
|
|
некоторой фу кции двух переменных u(x, y) , |
необходимо и достаточно, |
|||||||||||||||||||||||||||||||||||||||
|
|
чтобы ∂P = ∂Q . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
∂y |
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Докажем необходимость этого условия. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
Пусть du = Pdx + Qdy , |
тогда по определению дифференциала функции |
|||||||||||||||||||||||||||||||||||||||
|
|
двух переменных P = |
∂u |
, |
|
Q = |
|
∂u |
. Вычислим |
|
∂P |
|
= |
|
∂2u |
|
и |
∂Q |
= |
∂2u |
. |
|
||||||||||||||||||||
|
|
∂x |
|
|
∂y |
|
∂y |
|
|
∂y∂x |
|
∂x |
∂x∂y |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Известно, что вторые смешанные производные функции двух переменных р вны друг другу, если они непрерывны.

290 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
Лекции 10 - 11 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Так как |
∂P |
и |
∂Q |
|
непрерывны по условию: |
|
∂2u |
|
= |
|
∂2 |
|
|
|
, следователь- |
|||||||||||||||||||||||||||||||||||||||||
|
∂y |
|
∂x |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x∂y ∂y∂x |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
но, ∂P = ∂Q и Pdx + Qdy = 0 , du = 0 , откуда u(x, y) = c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
∂y |
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Основываясь на вышеизложенном, решим ДУ в полных дифференциа- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
лах. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решить ДУ |
2x |
dx + |
|
y2 −3x2 |
dy = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
y3 |
|
|
|
y4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Здесь |
P = |
2x |
, Q = |
|
y2 −3x2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
y3 |
|
|
|
|
y4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1). Проверим, является ли полным дифференциалом выражение, стоящее |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
в левой части ДУ. Вычислим |
∂P |
= − |
6x |
, |
∂Q = − |
6x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
y4 |
|
|
|
∂x |
|
y4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Видим, что |
∂P |
= |
∂Q |
, значит, |
2x |
dx + |
|
y |
2 −3x2 |
dy = du . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
∂y |
∂x |
|
y3 |
|
|
|
y4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2). Так как выражение, стоящее в левой части уравнения, является пол- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u |
= |
|
2x |
, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u |
|
|
|
|
∂u |
|
|
|
|
|
|
|
|
|
∂x |
|
y |
3 |
|
|
|
|
||||||||||
|
|
ным дифференциалом, значит, du = |
dx + |
dy , и |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
∂x |
∂y |
|
|
∂u |
|
|
|
|
y |
2 |
−3x |
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
. |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
y |
4 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
3). Интегрируя первое из уравнений системы, получаем: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
u(x, y) = ∫ |
2x |
dx +ϕ( y)с= |
x2 |
|
|
+ϕ( y) , где постоянная интегрирования по x |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
y3 |
y3 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
представляет с б й функцию ϕ( y) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
4). Для |
ахожде ия ϕ( y) |
|
|
|
продифференцируем по |
полученное для |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
u(x, y) |
|
|
|
|
|
|
|
|
|
|
∂u |
3x2 |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
выраже ие: |
|
|
∂y = − |
|
|
|
y4 |
+ϕ ( y) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
−3x2 |
|
3x2 |
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
5). Второе ур внение системы дает: |
|
|
|
|
|
|
|
|
|
= − |
|
|
|
|
|
+ϕ ( y) , |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
y4 |
|
|
|
|
y4 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
′ |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
откуда ϕ ( y) |
= |
|
, |
|
ϕ( y) = − |
|
|
+c1 |
, значит, u(x, y) |
= |
|
|
|
|
|
− |
|
|
|
+c1 |
и общим |
||||||||||||||||||||||||||||||||||
|
|
y2 |
|
y |
|
y3 |
|
y |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
интегралом ДУ является выражение |
|
|
x2 |
|
− |
1 |
= c . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
y3 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

|
Дифференциальные уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
ru |
|
291 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
10.2.7. Таблица 1. Решение ДУ первого порядка |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||
|
|
|
|
Вид уравнения |
|
|
antigtuy = u υ |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
Тип уравнения |
|
|
Метод решения |
|
|
||||||||||||||||
|
1. P(x)dx +Q( y)dy = 0 |
|
с разделяющимися |
непосредственное |
|
|
||||||||||||||||||||
|
|
переменными |
|
интегрирование |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2. |
y′ = f |
|
y |
|
|
|
u |
= |
y |
, y = u x , |
|
|
|||||||||||||
|
|
однородное |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x |
|
|
|
y′ = u′ x + u |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x = X +α, |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1x + b1 y + c1 |
|
|
|
y =Y + β; |
|
|
|
|
|
|||||||||||
|
3. |
y′ = f |
|
обобщенное |
|
a α + b β + c = 0, |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
a2 x + b2 y + c2 |
|
|
однородное |
|
a α |
+ b |
β + c |
2 |
= 0; |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
dY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ =Y′ = dX |
|
|
|
|
|
||||||||
|
4. |
y′ = P(x) y + Q(x) |
|
линейное по y(x) |
y |
′ |
= uυ |
′ |
|
′ |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ u υ |
|
|
|
|
|||||||
|
|
|
′ |
Скачано |
|
линейнсе по x( y) |
x = u υ |
|
|
|
|
|
|
|
||||||||||||
|
5. |
x |
= P( y)x + Q( y) |
|
′ |
|
|
|
′ |
|
|
|
′ |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
= u υ +uυ |
|
|
|
|
|
||||||
|
6. |
y′+ P(x) y = Q(x) yn |
|
Бер улли |
|
y = u υ |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
интегрирование |
|
|
|||||||||||
|
7. P( x, y)dx + Q( x, y)dy = 0 |
|
|
|
системы |
|
|
|
|
|
|
|||||||||||||||
|
∂P |
= ∂Q |
|
|
|
|
|
|
уравнение в полных |
|
∂u |
= P(x, y), |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
||||||||||||||
|
∂y |
|
∂x |
|
|
|
|
|
|
дифференциалах |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
du(x, y) = 0 |
|
|
|
|
∂u |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
= Q(x, y) |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

292 |
|
|
|
. |
ru |
Лекции 10 - 11 |
||
|
|
|
|
|
||||
|
10.2.8. Особые решения ДУ первого порядка |
|
|
|
|
|||
|
|
Если ДУ первого порядка не разрешено относительно производной, т.е. |
||||||
|
имеет вид F(x, y, y ) = 0 |
, то через некоторые точки плоскости (x, y) |
|
может про- |
||||
|
|
′ |
|
antigtu |
|
|
|
|
|
ходить не одна интегральная кривая, т.е. для некоторых начальных значений |
|||||||
|
может нарушиться единственность решения. |
|
|
|
|
|||
|
|
Линия L называется огибающей однопа- |
y |
|
|
|
||
|
О |
|
|
|
||||
|
|
раметрического |
семейства |
линий |
|
|
|
|
|
|
|
|
|
|
|||
|
|
Φ(x, y,c) = 0 , если она в каждой точке каса- |
|
|
|
x |
||
|
|
ется той или иной линии семейства, причем |
0 |
|
|
|||
|
|
|
|
|
||||
в различных точках линии L ее касаются различные линии данного семейства.
Для определения огибающей служат следующие два уравнения:
Φ(x, y,c) = 0,Φc′(x, y,c) = 0.
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть ДУ F (x, y, y ) = 0 (*) имеет общий интеграл Φ(x, y,c) = 0 (**). |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если это семейство интегральных кривых имеет огибающую, то оги- |
|||||||||||||||||||||||||||
бающая также является интегральной кривой ДУ. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
Уравнения Φ′(x, y,c) = 0, |
|
по ле и ключения параметра c , |
определяют |
||||||||||||||||||||||||
|
Φc (x, y,c) = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
функцию y =ψ(x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если эта функция уд влетв ряет ДУ (*) и не принадлежит семейству |
|||||||||||||||||||||||||||
(**), то она называется |
с бым решением ДУ. В каждой точке особого ре- |
||||||||||||||||||||||||||
шения нарушается единственн сть решения. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
Пример: |
Решите ДУ y2 |
(1+ y′2 )= R2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
R2 |
− y2 |
ydy |
|
|
|
= dx , (x −c) |
= ±∫ |
ydy |
|
|
||||||||||||
|
|
dx |
= ± |
|
|
y |
, |
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
± |
R |
|
− y |
|
|
|
|
|
|
R |
− y |
|
|||||||||
|
Вычислим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
∫ |
|
|
2 ydy |
= R2 − y2 = t = − |
1 |
∫ |
dt |
|
= |
|
|
|
|||||||||
|
|
|
|
|
2 |
|
|
2 2 |
2 |
t |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
R − y |
|
dt = −2 ydy |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 t 2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
= − |
∫t− |
|
dt = − |
= − t = − R2 − y2 . |
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
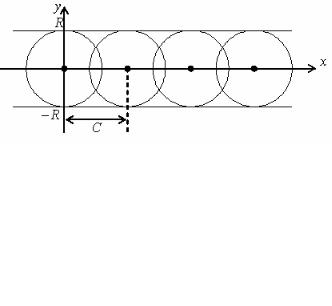
|
Дифференциальные уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
293 |
|||||||
|
|
|
Итак, x − c = ± |
R2 |
− y2 |
, |
(x − c)2 |
= R2 − y2 . |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Значит, Φ( x, y,c ) = (x − c)2 + y2 − R2 = 0 , 2( x − c )( −1) = 0 , |
|
|
|
|
||||||||||||||||
|
|
|
|
|
2 |
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( x − c ) |
|
+ y |
|
= R |
|
y2 |
= R2 , откуда y = ±R , y1 |
= R, y2 = −R |
|
|
||||||||||
|
|
|
x = c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, y = ±R – огибающие, которые удовлетворяют ДУ, являются особыми |
||||||||||||||||||||
|
|
|
решениями. |
|
|
|
|
|
|
|
|
|
|
|
|
. |
ru |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.1. ДУ высших порядков y( n ) = f (x,y,y′,...,y( n −1 ) ) |
|
|
|
|
|
|||||||||||||||||
|
|
Задача Коши заключается в нахождении решения ДУ n-го порядка, |
|||||||||||||||||||||
|
удовлетворяющего заданным начальным условиям: |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
y(x0 )= y0 , |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
y′(x0 )= y0′ , |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
#с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n−1) |
(n−1) |
. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
= y0 |
|
|
|
|
|
|
|
||
|
|
Теорема Коши (существования и единственности решения ДУ n-го по- |
|||||||||||||||||||||
|
Т |
||||||||||||||||||||||
|
|
рядка). Если в ДУ |
y( n ) |
= f |
(x, y, y′,..., y( n−1 ) ) |
функция f (x, y, y′,..., y( n−1 ) ) |
|||||||||||||||||
|
|
||||||||||||||||||||||
|
|
и ее частные производные по аргументам |
y, y′,..., y( n−1 ) |
|
непрерывны в |
||||||||||||||||||
|
|
некоторой обл сти, содержащей значения |
x = x0 , y = y0 , |
y′ = y0′, |
…., |
||||||||||||||||||
|
|
y( n−1 ) = y0( n−1 ) , |
то существует и притом единственное решение y = y( x ) |
||||||||||||||||||||
|
|
ДУ, удовлетворяющее начальным условиям: y( x0 ) = y0 , |
|
|
′ |
′ |
, …, |
||||||||||||||||
|
|
y ( x0 ) = y0 |
|||||||||||||||||||||
|
|
y( n−1 ) ( x0 ) = y0( n−1 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Общим |
решением |
|
ДУ |
|
n-го |
порядка |
называется |
функция |
|||||||||||||
|
О |
|
|
||||||||||||||||||||
|
|
y =ϕ( x,c1 ,c2 ,...,cn ), которая удовлетворяет ДУ при любых значениях |
|||||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
постоянных. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Частное решение ДУ (решение задачи Коши) может быть найдено из |
|||||||||||||||||||||
|
|
общего |
решения |
ДУ по |
заданным начальным |
условиям |
y( x0 ) = y0 , |
||||||||||||||||
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
294 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекции 10 - 11 |
|
′ |
′ |
y |
( n−1 ) |
( x0 |
|
|
|
( n−1 ) |
, из которых получаем систему уравнений: |
||||||||||||||||||
y ( x0 |
) = y0 , …., |
|
|
|
) = y0 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y(x |
0 |
, c0 |
,...c0 )= y |
0 |
, |
|
. |
ru |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
y′(x0 , c10 ,...cn0 )= y0′ , |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
. |
|
|
. |
|
|
. . |
0 ) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
y(n−1) (x |
0 |
, c0 |
,...c |
= y(n−1) |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
n |
|
0 |
|
|
|
|
|
||
для определения постоянных c0 |
,c0 |
,....c0 . |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
Решение задачи Коши для ДУ n-го порядка имеет вид: |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y =ϕ( x,c 0 |
,c 0 |
,...,c 0 ). |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
n |
|
|
|
|
|
11.2. ДУ второго порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решением ДУ |
y′′ = |
f ( x, y, y′) |
является функция |
y =ϕ( x,c1 ,c2 ) , пред- |
|||||||||||||||||||||||
ставляющая совокупность интегральных кривых. |
|
|
|
|
|
||||||||||||||||||||||
Задача Коши заключается и нахождении решения ДУ, проходящего че- |
|||||||||||||||||||||||||||
рез точку M 0 (x0 , y0 ): |
y (x0 ) = y0 в заданном направлении: tgα0 |
= y′(x0 ) = y0′ . |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
||||
11.3. Некоторые типы ДУ второго порядка, приводимые |
|||||||||||||||||||||||||||
|
к ДУ первого порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
11.3.1. ДУ y′′ = |
f ( x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Двукратное и тегрирова |
|
ие дает: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
y′ = ∫ f ( x )dx + c1 , y = ∫(∫ f ( x )dx)dx + c1 x + c2 . |
|
|
|
||||||||||||||||||||||
11.3.2. ДУ вида y′′ = |
f ( x, y′) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Уравнение |
d 2 y |
= f |
|
|
|
dy |
|
|
явно не содержит y(x). Сделаем замену пере- |
||||||||||||||||||
dx |
2 |
x, |
dx |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
менной: p(x) = |
dy |
, тогда |
|
dp |
= |
d 2 y |
и уравнение принимает вид |
dp |
= f ( x, p ), |
||||||||||||||||||
dx |
|
dx |
dx2 |
dx |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
от уда p = p (x,c1 ), |
y = |
∫ |
p (x,c1 )dx + c2 . |
|
|
|
|
|
|
|
|
|
|||||||||||||||
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

Дифференциальные уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
295 |
|||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Решите уравнение xy′′ = 2x − y′, если при x =1 |
|
y = 12 , |
|
|
y′ =1. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
dp |
|
|
|
|
|
dp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dpdx = 2 |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Если y′ = p |
, y′′ = dx |
, то |
x dx |
= 2x − p , |
|
|
− |
|
– |
однородное уравне- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
ние первого порядка. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
ru |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
p = ux , |
|
|
′ |
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
Тогда x = u |
, |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 |
− x |
принимает вид: |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= u x +u , и уравнение |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u x +u = 2 −u . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
du |
|
2(1−u) |
|
|
|
|
|
du |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
u x = 2(1−u), |
|
|
|
dx |
= |
|
|
|
x |
|
, |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
, ln c1 x |
= − |
|
|
|
ln(1−u) , |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2(1−u) |
|
x |
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
p |
|
|
|
|
1 |
|
|
|
|
|
|
p |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
′ |
|
|
||||||
|
|
|
c1x = 1−u , c1x 1− x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
1 , 1− x = c12 x2 , x =1− c12 x2 , p = x − c12 x = y |
, |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
dy = xdx − |
dx |
|
|
, откуда y |
= |
x2 |
|
− |
|
1 |
ln x |
+c . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
c2 x |
2 |
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Тогда y (x) = x − c2 x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из начальных условий: |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
= |
+c2 , |
|
c2 = 0, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
, |
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(1) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
|
|
|
|
|
|
|
|
= |
0. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′(1) =1 |
|
|
|
|
1 =1 |
|
c |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Значит, |
|
y = |
x2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
11.3.3. ДУ y′′ = |
f (y, y′) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Уравнение |
яв о |
|
|
е |
|
содержит |
|
|
независимую |
переменную |
x. |
Пусть |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
y′ = p( y ), т.е. |
dy = p( y ) = p (y (x)) |
является сложной функцией y , следова- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dp |
dp |
|
dy |
|
|
|
|
dp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dp |
|
|
|
|
|
|||||||||
тельно: y′′ = dx |
= dy |
dx |
= |
dy |
p |
. Уравнение принимает вид: |
|
p dy |
= |
|
f ( y, p ), |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
откуда p = p( y,c1 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Для н хождения y получили уравнение dy = p (y,c ), |
|
|
|
|
dy |
|
|
= dx и общий |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
p (y,c1 ) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
интеграл имеет вид Φ( x, y,c1 ,c2 ) = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решите ДУ |
|
′′ |
|
|
(y ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
y |
|
= |
|
|
y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
296 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекции 10 - 11 |
||
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
dp |
|
|
|
|
|
|
|
dp |
|
|
|
|
p2 |
|
dp |
|
p |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
Пусть y′ = p( y) , тогда y′′ = p |
|
|
|
|
и p |
|
|
|
|
|
|
= |
|
|
|
|
|
, p |
|
|
|
|
|
− |
|
= 0 . |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
dy |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
y |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p = 0, |
|
|
|
|
|
||||||||
|
|
|
|
|
|
Это уравнение равносильно совокупности решений |
dp |
|
|
|
|
p |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Решением первого уравнения совокупности dy = 0 является ru |
y = c . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dp |
|
|
|
p |
|
|
|
dp |
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
Найдем решение второго: |
|
|
= |
, |
|
|
= |
, |
ln |
|
p |
|
= ln |
|
y |
|
+ lnc |
( c ≠ 0 ) , |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
y |
|
|
|
|
|
p |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
p = dy = c y , dy = c ydx , |
dy |
= c dx |
, |
lny = c x + lnc |
( c |
|
|
≠ 0 ) , |
|
y = c ec2 x . |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
dx |
|
2 |
|
|
2 |
|
|
|
y |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
3 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Ответ: |
y |
= c , |
y |
2 |
= c ec2 x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
11.4. Таблица 2. Решение ДУ второго порядка, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
допускающих понижение порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
Вид ДУ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Метод решения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
1. |
y′′ = |
f (x) |
|
|
|
|
|
Последовательное интегрирование |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
y |
′′ |
= |
′ |
) |
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
′ |
= y |
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
f (x, y |
|
|
|
|
p(x) = y |
, p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
3. y′′ = f (y, y′) |
|
|
|
|
p( y) = y′, y′′ = |
dp |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
4. y′′ = |
y − xy′ |
|
|
|
|
|
p = |
y |
|
|
, p′ |
= |
|
|
y − xy′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
x2 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
5. yy′′+ y′2 = x |
|
|
|
|
p = yy′, p′ = y′2 + yy′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
11.5. ДУ n-го порядка, допускающие понижение порядка |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
11.5.1. ДУ вида y(n) |
= f ( x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Общее решение получается путем n-кратного интегрирования. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Принимая во внимание, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
y(n) = (y(n−1) )' , y(n−1) = ∫ f (x)dx + C1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
y(n−2) = ∫(∫ f (x)dx)dx +C1x +C2 , …, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
y = ∫...∫ f |
(x)dx...dx + |
C xn−1 |
|
|
+ |
|
C |
xn−2 |
|
|
+... + Cn . |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
(n −1)! |
(n − 2)! |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||

′′ |
1 |
2 x |
′ 1 2 x |
1 2 x |
x2 |
ru |
297 |
Дифференциальные уравнения |
|
|
|
|
|
||
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдите частное решение ДУ y′′′ = e2 x , удовлетворяющее начальным ус- |
|||||||||||||||||||||||||||||||||||||||
|
ловиям: y0 =1 , y0′ = −1 , |
y0′′ = 0 |
при x0 |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Последовательное интегрирование дает: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
y = |
2 |
e +c |
|
, y = |
4 |
e +c x +c |
, y |
= |
8 |
e |
|
+c |
|
|
|
+c x +c . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
1 2 |
.2 |
3 |
|
||||||||||
|
Из начальных условий y(0) =1 |
|
′ |
= −1, |
′′ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
, y (0) |
y (0) = 0 , что приводит к сис- |
||||||||||||||||||||||||||||||||||||||
|
теме для определения постоянных c1, c2 , c3 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
1 |
|
+c3 , |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 = |
|
|
|
|
|
|
|
|
c1 |
= − |
|
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
5 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
+ c2 |
, откуда |
|
|
|
|
|
|
и y = |
e |
2 x |
− |
x |
2 |
− |
x + |
. |
|
|
||||||||||||||||
|
−1 |
= |
|
|
|
|
c2 |
= − |
|
|
, |
8 |
|
4 |
|
4 |
8 |
|
|
|||||||||||||||||||||
|
|
4 |
|
|
|
4 |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
0 = 1 + c , |
|
|
|
|
|
c = 7 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
|
1 |
|
|
|
|
|
3 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдите |
|
общий |
интеграл |
|
уравнения |
|
y " = sin(kx) |
и |
частное |
решение, |
|||||||||||||||||||||||||||||
|
удовлетворяющее начальным условиям y |x=0 = 0, |
y ' |x=0 =1 . |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y ' = ∫sin kxdx +C1 = − 1 cos kx +C1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
|
|
− |
|
cos kx +C1 |
|
+ C2 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
k |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Скачано |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= −∫k cos kxdx + ∫C1dx +C2 |
= − |
k2 |
sin kx + C1x +C2 |
|
- |
общее решение. Из |
|||||||||||||||||||||||||||||||||
|
условия y |x=0 = 0 нах дим 0 = С2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Из условия y ' | |
x=0 |
=1 |
|
нах дим: |
1 = − 1 +C → C =1 + 1 . |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
Таким образом, част ое решение имеет вид: y = − |
sin kx |
|
1 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
k |
|
11.5.2. ДУ вида F (y, y ', y",..., y(n) )= 0
Уравнение не содержит в явном виде независимую переменную x . Порядок уравнения понижается на единицу подстановкой:
|
|
|
d |
|
|
|
|
|
y ' = P(y), y" = dP |
= dP dy |
= dP P, y '" = |
dP P |
= |
||||
|
||||||||
dx |
dy dx |
dy |
dx |
dy |
|
|
||
= P |
d 2 P dy |
+ |
dP dy dP |
= P |
2 d 2 P |
dP 2 |
||||
dy |
2 |
dx |
dy dx dy |
dy |
2 |
+ |
P . |
|||
|
|
|
|
|
dy |
|
||||

|
298 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
Лекции 10 - 11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
им |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ер: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдите общий интеграл уравнения y '2 + 2 yy " = 0 . |
|
|
|
. |
|
|
|
|||||||||||||||
|
|
Подстановка y ' = P (y) |
, y" = dP P |
|
|
|
|
antigtu |
|
|
|
|||||||||||||
|
|
в уравнение дает: |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dP (y) |
|
|
|
|
P (y)= |
dy |
= 0, |
y = const; |
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
P (y)+ 2 y |
|
P (y) |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
dy |
P + 2 y dP = 0; |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 y dP = −P, dP = − dy , ln |
P |
= − 1 ln |
y |
+ ln C , |
P = C y−12 |
= |
C1 |
, |
|
|
|
|
||||||||||
|
|
|
dy |
P |
2 y |
|
|
|
2 |
|
|
|
|
1 |
1 |
|
y |
|
|
|
|
|||
|
|
dy = |
C1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
; |
ydy = C dx; |
2 y 2 = C x +C |
. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
dx |
|
y |
|
1 |
3 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
11.5.3. ДУ вида F (x, y(k ),..., y(n) )= 0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Уравнение не содержит в явном виде функцию |
y и ее производные до |
|
||||||||||||||||||||
(k −1) порядка включительно. Порядок уравнения понижается на k единиц с |
|||||
|
с |
( |
x, P, P ',..., P(n−k ) |
) |
|
помощью замены |
y(k ) = P (x). Имеем F |
|
|
= 0. Если для по- |
|
следнего уравнения найдено решение P (x) = ϕ (x,C1 ,C2 ,...,Cn−k ), то искомая
функция y (x) получает я |
путем |
k - |
кратного |
интегрирования функции |
||||||||||||||||||||||||||
P (x) = ϕ (x,C1 ,C2 ,...,Cn−k ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример: |
Найдите общий интеграл уравнения xy '"+ y "− x −1 = 0 . |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
В урав е ии яв о |
е содержатся функции y, |
|
y ' . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Сделаем заме у |
y " = P (x) → y '" |
= dP . Подстановка приводит к линейному |
|||||||||||||||||||||||||||
|
|
P |
= 1 |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ур внению: P '+ |
+1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение ищем в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uυ |
|
|
1 |
|
|||||||
|
P (x) = u (x)υ (x), P ' = u 'υ +υ ' u, u 'υ +υ ' u + |
= |
|
+1, |
||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ |
|
|
1 + x |
|
|
|
x |
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ u |
'υ = |
, |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
u υ '+ |
|
|
x |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
υ '+υ |
= 0, |
dυ |
|
= − |
υ ; |
dυ |
|
= − dx , |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
dx |
υ |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|||||||
|
|
ln |
|
υ |
|
= −ln |
|
x |
|
→ υ = 1 , u 'υ = |
1+ x |
, |
u ' 1 |
= |
1+ x |
, |
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
x |
|
|
|
x |
|
|
|||||
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||

|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
∫ 4 |
|
|
|
|
|
|
|
|
|
|
|
ru |
|
299 |
|
|||||||
|
Дифференциальные уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
u ' =1 + x, du = (1 + x)dx, u = |
x2 |
+ x +C , P = uυ, P = |
x2 |
+ x +C |
|
1 |
, |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
. |
|
|
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
x |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
C |
x |
|
|
|
C |
|
x |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
P = |
|
|
+1 |
+ |
|
1 , y " = |
|
|
+1 + |
1 , y ' = |
|
|
|
+1 + 1 |
dx + C2 |
= |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
∫ |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
= |
+ x +C ln |
x |
+C |
|
, y = |
|
x2 |
+ x |
+C |
ln |
x |
+C |
2 |
dx +C |
3 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
u = ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
∫ln xdx = |
|
|
|
|
1 |
|
= x ln x − ∫x |
1 dx = x ln x − x = x (ln x −1); |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
du = x dx |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dυ = dx |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
υ = x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
y = |
x3 |
+ |
x2 |
|
+C1x (ln x −1)+C2 x +C3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
12 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
11.5.4. ДУ вида |
|
d |
|
G (x, y, |
y ',..., y(n−1) (x))= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Левая часть ДУ такого вида может быть представлена в виде полной |
|
||||||||||||||||||||||||||||||||||||||||||
|
производной по x |
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
от некоторой функции. Покажем, что интегрирование по |
|
|||||||||||||||||||||||||||||||||||||||||
|
x понижает порядок уравнения на единицу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Скачано |
|
(xy ")' = |
|
x2 |
+ x ', xy " = |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
xy |
'"+ y "− x |
−1 = 0, |
|
|
+ x +C , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
y " = |
x |
|
+1 + C1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
В результ те изучения м териала, изложенного в этих лекциях, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
студенты должны р злич ть и уметь решать: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
основные типы ДУ первого порядка, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
некоторые типы ДУ второго порядка, приводимые к ДУ первого порядка, |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
ДУ n-го порядка, допускающие понижение порядка. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Лекции 12 - 13 |
. |
ru |
|
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
В лекции рассмотрены линейные дифференциальные уравнения (ЛДУ) и методы их
решения. Особое внимание уделено линейным ДУ с постоянными коэффициентами, возникающим как простейшая математическая модель явления при рассмотрении многих задач естественных и прикладных наук.
12.1. Общая теория линейных дифференциальных уравнений высшего порядка. Определения и общие свойства
12.2. Решение ОЛДУ второго порядка с постоянными коэффициентами 12.3. Таблица 3. Решение ОЛДУ второго порядка
12.4. ОЛДУ n-го порядка с постоянными коэффициентами 12.5. Таблица 4. ОЛДУ n-го порядка
12.6. НЛДУ второго порядка 13.1. Решение НЛДУ второго порядка методом вариации
13.3.1. Метод неопределенных antigtuкоэффициентов 13.3.2. Метод вариации произвольной постоянной 13.3.3. Принцип уперпозиции
произвольных постоянных
13.2. Решение НЛДУ второго порядка с постоянными
коэффициентами методом неопределенных коэффициентов |
|
с |
y′′+ py′+ qy = f (x) |
13.3. Таблица 5. Решение НЛДУ |
|
Скачано13.4. НЛДУ высших порядков 13.4.1. Метод вариации произвольных постоянных
13.4.2. Метод неопределенных коэффициентов 13.5. Таблица 6. Решение НЛДУ n-го порядка
13.5.1. Мет д не пределенных коэффициентов 13.5.2. Мет д вариации произвольной постоянной
12.1. Общая теория линейных дифференциальных уравнений
высшего порядка. Определения и общие свойства
О |
Линейным называется ДУ, содержащее функцию у и ее производные в |
||
|
первой степени. |
|
|
|
|
|
|
О |
Неоднородным линейным дифференциальным уравнением (НЛДУ) |
||
|
n-го порядка называется ДУ вида: |
|
|
|
y(n) + a y(n−1) |
+... + a |
y = f (x) , |
|
1 |
n |
|
|
Линейные дифференциальные уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
301 |
|||||||||||||||||||
|
где ai |
(i =1,2,...,n) |
|
и f (x) |
- непрерывные функции от х или постоянные, |
|||||||||||||||||||||||||||||||||||
|
|
причем правая часть |
f (x) ≠ 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
|
||||||||||||||||||
|
|
Линейное ДУ называется однородным (ОЛДУ), если |
f (x) = 0 . |
|
||||||||||||||||||||||||||||||||||||
|
О |
|
||||||||||||||||||||||||||||||||||||||
|
|
Рассмотрим ОЛДУ второго порядка: |
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′′+ a1 y′+ a2 y = 0 . |
|
|
|
|
|
|
|
|||||||||||||
|
|
Пусть y1 = y1(x) |
и y2 = y2 (x) |
- частные решения ДУ. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
О |
Два решения ДУ |
y и y |
|
называются линейно независимыми, |
если их |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
линейная комбинация c1 y1 + c2 y2 = 0 лишь в случае c1 = c2 = 0 . |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
Решения |
|
y1 и |
y2 будут линейно зависимы тогда и только тогда, когда |
|||||||||||||||||||||||||||||||||||
|
|
|
y2 = cy1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Например, |
функции |
y |
= ex |
и y |
2 |
= 3ex |
- линейно зависимы, а функции |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
y |
= ex |
и |
y |
2 |
|
= e−x - линейно независимы. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Если |
|
y1 |
|
|
и |
|
y2 |
являются |
|
|
|
|
функциями |
x , |
то |
определитель |
||||||||||||||||||||||
|
О |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
W (y1, y2 )= |
|
y1 |
|
y2 |
|
= y1 y2′ − y1′y2 называется определителем Вронского. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y1′ |
y2′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W (y1, y2 )≡ 0 , |
||||||||||
|
Т |
Если функции |
|
y1 |
|
и |
y2 |
|
линейно зависимы на [a,b] , |
то |
||||||||||||||||||||||||||||||
|
|
|
x [a,b] . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
|
y2 |
|
y1 |
λy1 |
|
|
|
y1 |
y1 |
|
|
|
||||||||||||
|
|
|
y2 = λy1 → y2′ = λy1′ и W (y1, y2 ) |
|
= |
|
= |
= λ |
|
= 0 . |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1′ y2′ |
|
y1′ |
λy1′ |
|
|
|
y1′ |
y1′ |
|
|
|
|||
|
|
Если |
|
реше ия |
y1 |
и |
|
|
|
y2 |
ДУ |
|
|
|
линейно |
независимы |
на |
[a,b] , то |
||||||||||||||||||||||
|
Т |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
W (y1, y2 )≠ 0, x [a,b] . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Доказательство: |
|
|
|
|
W (y1, y2 )= 0 , |
|
тогда |
y1 y2′ − y1′y2 = 0 . Для |
y1 ≠ 0 : |
|||||||||||||||||||||||||||||
|
|
Допустим противное: |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
y y′ |
− y′y |
|
|
|
|
|
|
|
|
y |
2 |
|
′ |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
2 |
|
1 |
|
2 |
= 0 , |
т.е. |
|
|
= 0 и |
|
|
|
|
2 |
= const , |
что противоречит условию, |
||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
y1 |
|
|
|
|
|
|
|
|
|
|
y1 |
|
|
|
|
|
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
зн чит, W ≠ 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Если y1 и y2 - |
линейно независимые частные решения ОЛДУ второго |
|||||||||||||||||||||||||||||||||||||
|
Т |
|||||||||||||||||||||||||||||||||||||||
|
|
порядка |
y′′ |
+ a1 y′+ a2 y = 0 , то общее решение ДУ равно линейной ком- |
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
302 |
|
|
|
|
(c1 y1 + c2 y2 )″ + a1 (c1 y1 + c2 y2 )′ + a2 (c1 y1 + c2 y2 )= |
ru |
Лекции 12 - 13 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
бинации этих частных решений |
y = c1 y1 + c2 y2 , где c1,c2 |
- произвольные по- |
||||||||||||||||||||
|
стоянные. |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
y1′′+ a1 y1′ + a2 y1 = 0, y2′′ + a1 y2′ + a2 y2 = 0. |
|
|
|
|
|
y1 , то второе |
||||||||||||||||
|
Т |
|
Если известно одно ча тное решениеantigtuОЛДУ 2-го порядка |
||||||||||||||||||||
|
Подставим решение в виде y = c1 y1 + c2 y2 |
в исходное уравнение: |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
= c1 (y1′′+ a1 y1′ + a2 y1 )+ c2 (y2′′ + a1 y2′ + a2 y2 ) = c1 0 + c2 0 = 0 , |
|
|
|
|
||||||||||||||
|
|
|
значит, |
|
y = c1 y1 + c2 y2 |
- общее решение ОЛДУ при любом выборе посто- |
|||||||||||||||||
|
|
|
янных. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Решите уравнение (x −1)y′′− xy′+ y = 0 . |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
= ex |
|
|
|
|
|
|
|
|
|
Подстановкой |
в уравнение убеждаемся, что |
функции |
y = x, |
y |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
удовлетворяют уравнению, причем |
≠ const |
, т.е. они линейно незави- |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
с |
|
y |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
симы, значит y = c x +c ex . |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
частное решение, |
линейно незави имое с первым, находится интегриро- |
|||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
ванием линейного дифференциального уравнения (ЛДУ) первого поряд- |
||||||||||||||||||||
|
|
|
ка. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Пусть |
|
|
y′′+ a1 y′+ a2 y = 0 ; |
|
y1 |
- |
частное |
решение, |
значит, |
|||||||||||
|
|
|
y1′′+ a1 y1′ + a2 y1 = 0 . Второе частное решение ищем в виде y2 = u(x) y1 , где |
||||||||||||||||||||
|
|
|
u(x) |
- неизвест ая фу |
кция. |
(y1′′+ a1 y1′ + a2 y1 ) u + y1u′′+ (2 y1′ + a1 y1 )u′ = 0 , |
|||||||||||||||||
|
|
|
Подставим y2 |
в |
ДУ: |
|
|||||||||||||||||
|
|
|
y1u′′+ ( |
2 y1′ + a1 y1 )u′ = 0 . Заменой u′ = p , приходим к ДУ первого порядка |
|||||||||||||||||||
|
|
|
для н хождения функции р: |
y1 p′+ ( |
2 y1′ + a1 y1 ) p = 0 , интегрирование ко- |
||||||||||||||||||
|
|
|
торого |
|
|
позволяет |
найти |
функцию |
|
u(x) |
и |
y2 = u(x) y1 , |
|
т.е. |
|||||||||
|
y2 = y1 ∫ |
e−∫a1dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12.2. Решение ОЛДУ второго порядка с постоянными оэффициентами
Рассмотрим уравнение

|
Линейные дифференциальные уравнения |
|
|
|
|
|
|
|
|
ru |
303 |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
y′′+ py′+ qy = 0 . |
. |
|
|
(*) |
|||||||
|
Ищем его решение в виде y = ekx |
|
|
|
|
|
|
|
|
k . |
||||||
|
(подстановка Эйлера), найдем значения |
|||||||||||||||
|
Продифференцируем y : |
y′ = kekx , |
y′′ = k2ekx . Подстановка такого вида реше- |
|||||||||||||
|
ния в ДУ дает: k2ekx + pkekx + qekx |
= 0 , k2 + pk + q = 0 . |
|
|
|
|
||||||||||
|
|
Уравнение |
|
|
|
|
|
|
antigtu |
|
|
|
|
|||
|
О |
|
|
2 |
|
|
|
|
|
(**) |
||||||
|
|
|
|
k x |
k x |
|
|
|
|
|
||||||
|
|
|
|
|
k |
+ pk + q = 0 |
|
|
|
|||||||
|
|
называется характеристическим уравнением ОЛДУ для определения |
||||||||||||||
|
|
k . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решения характеристического уравнения имеют вид: |
|
|
|
|
||||||||||
|
|
|
|
|
k |
|
= − |
p |
± |
|
p2 |
− q . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1,2 |
|
2 |
|
4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Возможны следующие виды решений: |
|
|
|
|
|
|
|
|||||||
|
1). Если D = |
p2 |
− q > 0 , то характеристическое уравнение имеет два действи- |
|||||||||||||
|
4 |
|||||||||||||||
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
тельных различных корня k1 и k2 , |
|
|
|
|
|
|
|
|
|
||||||
|
k1 ≠ k2 . |
|
|
|
|
|
|
|
||||||||
В этом случае ОЛДУ имеет два линейно независимых ( k1 ≠ k2 ) различных частных решения y1 = e 1 , y2 = e 2 . Общее решение ДУ имеет вид:
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
p2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
k x |
|
|
|
k |
|
x |
, где k |
|
|
|
|
|
− q . |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
y = c e 1 |
|
+ c e |
2 |
|
|
|
= − |
|
|
|
± |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1,2 |
|
|
|
2 |
|
|
4 |
|
|
|
|
|
|
|
|
||||
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Найдите реше ие ОЛДУ y′′− 2 y′−8y = 0 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
k 2 − 2k −8 = 0, k1 = 4, k2 = −2, y = c1e4 x + c2e−2x . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
2). Если D = |
p2 |
− q = 0 , то k |
= k |
2 |
|
и характеристическое уравнение имеет ко- |
|||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
рень k = − |
|
кратности два. Одно частное решение имеет вид: |
y = e− |
2 |
x |
. Вто- |
|||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
рое линейно независимое частное решение ищем в виде: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
= y u(x) = e− |
|
x |
u , |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тогда |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
− |
x |
|
|
|
|
|
− |
|
x |
|
p |
|
|
|
|
− |
x |
|
p |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
y2′ = e |
2 |
|
u′ |
+ e |
|
|
|
|
2 |
− |
|
|
u = e |
2 |
u′− |
|
|
u |
, |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
′′ |
|
′ |
|
p2 |
|
|
|
|
′ |
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
|
||
304 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекции 12 - 13 |
|
|
|
|
|
|
|
− |
p |
x |
|
|
p |
|
|
|
p |
|
− |
p |
x |
|
|
p |
|
− |
p |
x |
|
|
|
p2 |
|
|
|||||
|
|
|
y2′′ = e |
|
2 u′′− |
|
|
u′ |
− |
|
|
e |
2 |
u′− |
|
u = e |
2 |
|
u′′− p |
′+ |
|
|
|
|
. |
||||||||||||
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
. |
|
4 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
После |
|
подстановки |
|
|
в |
ОЛДУ |
и |
|
|
сокращения |
на |
|
e− |
2 |
x |
получим |
|||||||||||||||||||||
u |
− pu + |
|
u + pu − |
|
|
u + qu = 0 , и уравнение для |
(x) |
принимает вид: |
|||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u′′+ q − |
|
|
u = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В рассматриваемом случае равных корней характеристического уравнения
|
|
|
|
|
p |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
||
D = q − |
|
|
= 0 , и тогда u′′ = 0, |
|
u′ = C1, |
|
|
u = C1x + C2 , y2 = (C1x +C2 )e− |
|
x . По- |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ложим, C =1, |
C |
|
= 0 , тогда |
y |
|
= xe− |
|
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Общее решение ОЛДУ в случае k1 = k2 = k имеет вид: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = ekx (c1 + c2 x), где k = − |
p |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
y |
|
|
= xekx |
2 |
|
|
|
|
|
|
|
|
|
|||||||
! |
|
Убедиться в том, что выражение |
|
2 |
|
является вторым линейно не- |
|||||||||||||||||||||||||||||||||||||||||
|
|
зависимым решением дифференциальногоantigtuуравнения при условии, что |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
k = − |
p |
|
является решением характеристического уравнения, |
можно не- |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
посредственной подстановкой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
y′′−6 y′+ 9 y = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
k 2 − 6k + 9 = 0, k1 = k2 = 3 ± 9 − 9 = 3, y = (c1 + c2 x)e3x . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
3). Если |
D = |
p2 |
− q < 0 , то характеристическое уравнение имеет два сопря- |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
||||||||
женных комплексных корня k |
|
= − |
|
|
|
± i |
|
q − |
|
|
, k =α + βi, k |
2 |
=α − βi , где |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2 |
|
|
2 |
|
|
|
|
|
|
|
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
α = − |
p |
, |
β = |
q − |
p2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ч стные решения имеют вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = e(α+βi) x , |
|
y |
2 |
= e(α−βi) x . |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общее решение |
|
y = |
|
e(α+βi) x + |
|
e(α−βi) x |
= eαx ( |
|
eiβx + |
|
e−iβx ), где |
|
и |
|
- та- |
||||||||||||||||||||||||||||||||
|
c1 |
c2 |
c1 |
c2 |
|||||||||||||||||||||||||||||||||||||||||||
|
c1 |
c2 |
|||||||||||||||||||||||||||||||||||||||||||||
кие комплексные постоянные, что у – действительная функция. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Линейные дифференциальные уравнения |
|
|
|
|
|
|
|
|
ru |
305 |
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
По формуле Эйлера: eiβx = cos β x +i sin β x , |
e−iβx = cos β x −i sin β x , тогда |
|||||||||||||||||||
y = eαx ( |
|
+ |
|
)cos βx +i ( |
|
− |
|
)sin βx . Полагая |
|
+ |
|
= c1 , |
. |
i( |
|
|
− |
|
)= c2 , |
|
c1 |
c2 |
c1 |
c2 |
c1 |
c2 |
|
c1 |
|
c2 |
|||||||||||
c1,c2 - действительные постоянные, получим общее решение ОЛДУ в виде |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
||||||||
|
|
y = eαx (c cos β x + c sin β x), где k |
|
= − |
p |
± i |
|
q |
− |
p2 |
=α ± i |
β |
|||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
1,2 |
2 |
|
|
|
|
4 |
|
|
|
|
||||||
4). В частном случае |
|
y′′+ β2 y = 0 , когда |
p = 0, |
q = β2 , α = 0 , k1,2 |
= ±βi , об- |
||||||||||||||||||||||||||
щее решение имеет вид: y = c1 cos βx + c2 sin βx . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′′− 6 y′+13y = 0 . |
|
|
|
y = e3x (c1 cos 2x + c2 sin 2x). |
|
|
|||||||||||||||||||||
|
|
|
|
k 2 − 6k +13 = 0, k = 3 ± 2i, α = 3, β = 2 , |
|
|
|||||||||||||||||||||||||
12.3. Таблица 3. Решение ОЛДУ второго порядка |
|
|
|
|
|||||||||||||||||||||||||||
|
|
y′′+ py′+ qy = 0, k 2 + pk + q = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Корни характеристического уравнения |
|
|
|
|
|
Вид общего решения |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Скачано |
k1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
p |
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1. D > 0, k = − |
2 |
|
± |
4 |
|
− q = |
k2 |
- |
|
|
|
|
y = c1e |
k x |
+ c2e |
k x |
|
|
|||||||||||||
|
|
|
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
действительные, разные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2. k = k = k = − |
p |
|
- |
|
|
|
|
|
|
|
|
|
|
|
y = (c1 + c2 x)e |
kx |
|
|
|||||||||||||
1 |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
действительные, рав |
|
ые, крат ость 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3. k =α ±iβ, α = − |
p |
, |
|
β = |
q − |
p2 |
- |
|
|
|
y = e |
αx |
(c1 cos β x + c2 sin β x) |
||||||||||||||||||
1,2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|||||||||||
|
комплексные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4. k1,2 |
= ±iβ, α = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
y = c1 cos β x + c2 sin β x |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
306 |
|
|
|
|
|
|
|
|
|
|
|
|
ru |
Лекции 12 - 13 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
12.4. ОЛДУ n-го порядка с постоянными коэффициентами |
|
||||||||||||||||
|
|
|
y( n) + a1 y( n-1) + ...+ an y = 0, |
ai |
= const |
|
|
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Функции ϕ1(x), |
ϕ2 (x),...,ϕn (x) называются линейно независимыми, ес- |
||||||||||||||
|
О |
|
||||||||||||||||
|
|
|
ли никакая |
из |
них |
линейно |
не |
выражается |
через другие для |
всех |
||||||||
|
|
|
||||||||||||||||
|
|
|
x [a,b] , т.е. |
c1ϕ1 + c2ϕ2 +... + cnϕn |
≠ 0 , |
если ci - |
постоянные, не все рав- |
|||||||||||
|
|
|
ные нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если функции |
y1, y2 ,..., yn являются линейно независимыми частными |
||||||||||||||
|
Т |
|
||||||||||||||||
|
|
|
решениями |
ОЛДУ |
n-го |
порядка, |
то его |
|
общее решение |
есть |
||||||||
|
|
|
|
|||||||||||||||
|
|
|
y = c1 y1 + c2 y2 +... + cn yn , |
где |
ci |
- произвольные постоянные. Число ли- |
||||||||||||
|
|
|
нейно независимых частных решений ДУ равно степени характеристи- |
|||||||||||||||
|
|
|
ческого уравнения или порядку ОЛДУ. Найдя n частных решений, мож- |
|||||||||||||||
|
|
|
но записать общее решение ОЛДУ. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
Составим характеристическое уравнение ОЛДУ n-го порядка с постоян- |
|||||||||||||||
|
|
|
ными коэффициентами: |
kn + a k −1 + a |
k −2 +... + a |
n |
= 0 . Найдем его корни |
|||||||||||
|
|
|
k1,k2 ,...,kn . |
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В зависимости от корней характеристического уравнения частные ли- |
|||||||||||||||
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нейно независимые решения ОЛДУ имеют разный вид. |
|
|
|
||||||||||||
|
1). Каждому действительному однократномуantigtuкорню k соответствует частное |
|||||||||||||||||
|
решение вида y = ekx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Скачано |
|
|
|
|
|
кратности r |
|
соответствует r линей- |
||||||||
|
2). Каждому действительному корню k |
|
||||||||||||||||
|
но независимых решений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
= e |
kx |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
y2 = xekx , |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
y |
= x2ekx , |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
................... |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
= xr−1ekx |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
yr |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3). К ждой п ре комплексных корней k1,2 =α ±iβ соответствуют два частных решения:
y1 = eαx cos β x,y2 = eαx sin β x.
|
Линейные дифференциальные уравнения |
|
|
|
|
|
|
|
|
|
|
ru |
307 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
4). Каждой паре комплексных корней k1,2 |
=α ±iβ кратности µ соответствует |
|
||||||||||||
|
2µ частных решений: |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
αx |
cos β x, |
|
|
|
|
|
|
|||||
|
y1 = e |
|
|
|
|
|
|
|
|||||||
|
k n + a1k n-1 + a2 k n-2 + ...+ an |
= 0 |
|
|
antigtu |
|
|
|
|
||||||
|
y2 = xeαx |
cos β x, |
|
|
|
|
|
|
|||||||
|
.......... |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yµ = xµ−1eαx cos β x, |
|
|
|
|
|
|
||||||||
|
|
|
= eαx sin β x, |
|
|
|
|
|
|
||||||
|
yµ+1 |
|
|
|
|
|
|
||||||||
|
|
|
= xe |
αx |
sin β x, |
|
|
|
|
|
|
||||
|
yµ+2 |
|
|
|
|
|
|
|
|||||||
|
.......... |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
= x |
µ−1eαx sin β x. |
|
|
|
|
|
|
|||||
|
y |
2µ |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12.5. Таблица 4. ОЛДУ n-го порядка |
|
|
|
|
|
|
||||||||
|
y( n) + a1 y( n-1) + a2 y( n-2 ) |
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ ...+ an y = 0, ai = const , |
|
|
|
|
||||||||||
|
Скачано |
|
|
|
|
|
|
|
Вклад указанных корней в общее |
|
|||||
|
Корни характеристического уравнения |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
решение ДУ |
|
|
|
||
|
1. Действительные, разные |
|
|
|
|
|
|
|
y = c ek1x |
+ c ek2 x |
+... + c ekn x |
|
|
||
|
k1 ≠ k2 ≠ k3 ≠... ≠ kn |
|
|
|
|
|
|
|
1 |
2 |
|
n |
|
|
|
|
2. Действительные, крат ости r ≤ n |
|
|
|
|
|
y = (c1 + c2 x + c3 x2 +... + cr xr−1 )ekx |
|
|||||||
|
k1 = k2 = k3 =... = kr = k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Комплексные, р зные |
|
|
|
|
|
|
|
y = eα1x (c1 cos β1x + c2 sin β1x)+ |
|
|
||||
|
k1 =α1 ±iβ1, k2 =α2 ±iβ2 ,... |
|
|
|
|
|
|
|
+eα2 x (c3 cos β2 x + c4 sin β2 x)+... + |
|
|||||
|
..., kn =αn ±iβn , α1 ≠α2 ≠ ... ≠αn |
, |
|
|
|
|
+eαn x (c2n−1 cos βn x + c2n sin βn x). |
|
|
||||||
|
β1 ≠ β2 ≠ ... ≠ βn . |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
4. Комплексные, кр тности r = 3 |
|
|
|
|
|
|
y = eαx [ |
(c1 + c2 x + c3 x2 )cos β x + |
|
|||||
|
k1 = k2 = k3 =α + iβ |
|
|
|
|
|
|
|
+(c4 + c5 x + c6 x |
2 |
) sin β x ] |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

308 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекции 12 - 13 |
||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Решите уравнение y′′′− y = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k −1) |
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Характеристическое уравнение: |
k3 −1 = 0, |
k 2 + k +1 = 0 , |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
) |
ru |
|
|
|
|
|
|
|
|
|||
|
|
|
откуда k =1 |
, k |
|
= − 1 |
±i |
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
||||
|
|
|
Частные решения имеют вид: |
y |
= ex , |
|
y |
|
= e− |
|
cos |
|
|
3 |
x , y |
= e− |
|
sin |
3 |
x . |
|||||||||||||||||||
|
|
|
2 |
2 |
|
|
2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
− |
x |
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Общее решение имеет вид: |
y = c1e |
|
+ e 2 |
c2 cos |
|
|
|
x + c3 sin |
|
|
|
x . |
|
|
|
|
||||||||||||||||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
12.6. НЛДУ второго порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
НЛДУ второго порядка имеет вид: |
y′′+ a1 y′+ a2 y = f (x) , где ai и |
f (x) - |
||||||||||||||||||||||||||||||||||||
известные функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Т Общее решение НЛДУ y |
|
= y |
|
равно сумме общего решения y |
|
= |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
y |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
O.H . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O.O. |
|
|
|
||
|
соответствующего однородного уравнения |
|
y′′+ a1 y′+ a2 y = 0 и частного |
||||||||||||||||||||||||||||||||||||
|
решения |
yЧ.Н. = y |
|
данного |
|
|
|
неоднородного |
|
|
|
|
уравнения |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
y′′+ a1 y′+ a2 y = f (x) , то е ть y = y + y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Доказательство: |
|
|
y′′+ a1 y′ |
|
|
|
|
|
|
|
|
|
y′′+ a1 y′+ a2 y = f (x) . Сложим |
|||||||||||||||||||||||||
|
Для y , y |
справедливо: |
+ a2 y = 0, |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
+ y)′ + a2 (y + y)= f (x) , значит, |
|||||||||||||||||||||||
|
эти уравнения п членно: (y |
+ y)″ + a1 (y |
|||||||||||||||||||||||||||||||||||||
|
y = y + y является |
бщим решением НЛДУ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
13.1. Решение НЛДУ второго порядка методом вариации |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
произвольных постоянных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Пусть известно общее решение ОЛДУ |
y = c1 y1 + c2 y2 , где c1,c2 − const . |
|||||||||||||||||||||||||||||||||||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Найдем общее решение НЛДУ методом вариации произвольных постоянных. Будем иск ть общее решение НЛДУ в виде y(x) = c1 (x) y1 + c2 (x) y2 , считая c1
и c2 |
неизвестными функциями x . Найдем c1(x), c2 (x) . |
Вычислим производ- |
ную: |
y′ = c1 y1′ + c1′y1 + c2 y2′ + c2′y2 . Подберем c1(x) и |
c2 (x) так, чтобы |
c1′y1 + c2′y2 = 0 , тогда y′ = c1 y1′ + c2 y2′ , а y′′ = c1 y1′′+ c1′y1′ + c2 y2′′ + c2′y2′ .
Линейные дифференциальные уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
309 |
||||||||||||
|
Подстановка этих выражений в НЛДУ дает: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
(c1 y1′′+ c1′y1′ + c2 y2′′ + c2′y2′ )+ a1 (c1 y1′ + c2 y2′ )+ a2 (c1 y1 + c2 y2 ) = f (x) , |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
c1 (y1′′+ a1 y1′ + a2 y1 )+ c2 (y2′′ + a1 y2′ + a2 y2 )+ c1′y1′ + c2′y2′ = f (x) |
ru |
|
|
||||||||||||||||||||||||||||||||||||||||||
Выражения в круглых скобках равны нулю, так как |
|
y1 и y2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
- частные реше- |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c1′y1′ + c2′y2′ |
= f (x) . |
. |
|
|
|
|||||||||||||
ния соответствующих ОЛДУ. |
Значит, |
|
|
|
|
Получаем, |
что |
|||||||||||||||||||||||||||||||||||||||
|
yO.H . = c1(x) y1 + c2 (x) y2 , если c1(x) и c2 (x) |
|
|
удовлетворяют системе: |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
c′y |
|
|
+ c′y |
2 |
|
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
′ |
′ |
|
|
|
′ |
|
′ |
= f (x). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
c1 y1 |
+ c2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Для линейно независимых |
функций |
|
|
|
|
|
y1 |
|
|
и |
|
|
y2 |
|
определитель системы |
|||||||||||||||||||||||||||||||
|
∆ =W (y1, y2 ) ≠ 0 , |
и можно найти решение системы: c1′ =ϕ1(x), |
c2′ =ϕ2 (x) и |
|||||||||||||||||||||||||||||||||||||||||||
искомые функции c1(x) = ∫ϕ1(x)dx + c1, |
|
c2 (x) = ∫ϕ2 (x)dx + c2 . |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Найдите решение НЛДУ: |
y′′− |
y′ |
|
= x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
′ |
|
|
|
|
|
antigtu |
|
|
|
|
|
|||||||||||||||
|
|
|
Найдем решение ОЛДУ: y′′− |
|
|
= 0 , |
|
|
y′′ |
|
1 |
, ln y′ = ln x +ln c , |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
x |
|
|
|
y′ |
x |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
y′ = cx , yO.O. = c1x2 +c2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Частные решения ОЛДУ: |
y |
= x2 , |
|
|
y |
2 |
|
=1. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Найдем yO.H . = c1 (x) y1 + c2 |
(x) y2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
c′y |
+c′y |
|
= |
0, |
|
c′ x2 |
+c′ |
1 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
1 1 |
2 |
|
2 |
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
c1′y1′ +c2′y2′ = f (x), |
|
2c1′ x +c2′ 0 = x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
Отсюда c1′ = 1 , c2′ |
= − |
1 x2 , |
|
c1 = |
x |
+c1, |
|
c2 |
= − |
x3 |
+c2 . |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|||||
|
|
|
y |
= |
x |
|
+c |
x2 + |
− |
x3 |
|
|
+c |
|
1 = |
x3 |
|
− |
x3 |
+ c x2 |
|
+ c = |
x3 |
+c x2 |
+c . |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
O.H . |
|
|
1 |
|
|
6 |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
6 |
|
|
1 |
2 |
|
3 |
1 |
2 |
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
13.2. Решение НЛДУ второго порядка с постоянными |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
коэффициентами методом неопределенных |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
оэффициентов y′′+ py′+ qy = f ( x) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
Ранее (п. 12.6) |
|
доказано, |
|
что |
|
общее |
|
|
решение НЛДУ |
имеет |
вид: |
||||||||||||||||||||||||||||||||||
|
yO.H . = yO.O. + yЧ.Н. |
= y + y , где |
y |
- общее решение соответствующего ОЛДУ, |
||||||||||||||||||||||||||||||||||||||||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

310 |
|
|
|
|
|
Лекции 12 - 13 |
характеристическое уравнение которого k2 + pk + q = 0 , а |
y |
- частное реше- |
||||
ние НЛДУ. |
|
|
|
. |
|
|
|
|
|
|
|
|
|
Частное решение НЛДУ y может быть найдено методом неопределен- |
||||||
ных коэффициентов для некоторых видов функции |
f (x) |
в правой части |
||||
|
antigtu |
|
|
|
|
|
уравнения и корней характеристического уравнения его левой части |
||||||
Рассмотрим следующие случаи: |
|
|
|
|
ru |
|
1. Если f (x) = aeαx , a ≠ 0 , то y нужно искать в виде |
y = Aeαx , где А – |
|||||
произвольная постоянная, подлежащая определению. Последовательное
дифференцирование дает: y′ = Aαeαx , y′′ = Aα2eαx . |
Подставляя эти выраже- |
|||||
ния в НЛДУ и сокращая на eαx , получим |
|
|
|
|
||
|
|
A(α2 + pα + q)= a . |
|
|
|
(*) |
1). |
Если α не является корнем характеристического уравнения, т.е. |
|||||
|
2 |
+ pα + q ≠ 0 , то уравнение (*) имеет решение A = |
a |
αx |
|
|
α |
|
|
и y = Ae |
. |
||
|
α2 + pα + q |
|
||||
2). |
Если α является корнем характеристического уравнения, |
то y нужно |
||||
искать в другом виде. Так, если α - простой (однократный) корень характе-
ристического уравнения, то y = Axeαx ; е ли α - |
двукратный корень характе- |
|||||||||||||||||||||||||||
ристического уравнения, то y = Ax2eαx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Скачано |
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Найдите решение НЛДУ |
y |
′′ |
− |
′ |
+ 6 y |
= e |
x |
. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
5y |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Для ОЛДУ y′′−5y′+ 6 y = 0 , k 2 −5k + 6 = 0 , |
k1 = 3, k2 |
= 2 и y = c1e3x + c2 e2x . Для |
||||||||||||||||||||||||
|
|
f (x) = e |
x |
α =1, |
так как k1, k2 ≠ α |
, то |
~ |
= |
|
Ae |
x |
|
~ |
Ae |
x |
~ |
x |
. |
|
|||||||||
|
|
|
y |
|
|
. Найдем А. y ′ = |
|
, y ′′ = Ae |
|
|
||||||||||||||||||
|
|
Подста |
|
овка в урав ение дает: |
Aex −5Aex |
+ 6Aex |
= ex , откуда 2 A = 1, A = 1 |
и |
||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
~ |
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
y = |
2 e |
|
|
y = y + y = c1e |
|
+ c2 e |
|
+ |
1 |
e |
|
. |
|
|
|
|
|
|
|
|
|
|||||
|
|
Оконч тельно, |
3x |
2 x |
x |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2. f (x) = ax2 + bx + c = P (x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ч стное решение ищем в виде y = Q (x) = Ax2 + Bx + C ; найдем A, B, C. |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ = 2Ax + B, |
y′′ = 2A, |
2A + 2Apx + pB + Aqx2 + Bqx + Cq = ax2 + bx + c , |
|
|
|
||||||||||||||||||||||
|
|
Aqx2 + (2Ap + Bq)x + (2A + Bp + Cq) = ax2 + bx + c . |
|
|
|
|
|
|
||||||||||||||||||||

Линейные дифференциальные уравнения |
|
|
. |
ru |
311 |
|
|
|
|
|
|||
Неопределенные коэффициенты находятся из системы: |
|
|
|
|||
|
Aq = a, |
|
|
|
|
|
|
|
|
|
|
|
|
|
2Ap + Bq = b, |
|
|
|
|
|
|
antigtu2 |
|
|
|
||
|
2A + Bp +Cq |
= c. |
|
|
|
|
1). Если число «0» не является корнем характеристического уравнения, то y = Ax2 + Bx + C ;
2). Если число «0» является простым корнем характеристического уравнения, тогда частное решение нужно искать в виде y = x(Ax2 + Bx + C ).
3). Если число «0» является двукратным корнем характеристического уравнения, тогда y = x2 ( Ax2 + Bx + C) .
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решите ДУ |
y |
′′ |
= x |
2 |
+ y , если y(0) = −2, |
′ |
|||
|
|
|
|
|
y (0) =1. |
|||||||
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
Для ОЛДУ y′′− y = 0, |
k2 −1 = 0, k1 =1, |
k2 = −1 и y = c1ex +c2e−x . |
|||||||
|
|
|
Так как |
f (x) = x2 , y = Ax2 + Bx +C . |
|
|
||||||
|
|
|
Значит, |
2A −( Ax2 + Bx +C) = x2 . |
|
|
||||||
|
|
|
−A =1, |
|
|
|
|
|
|
|
|
|
|
|
|
−B = 0, |
откуда A = −1, B = 0,C = −2 и y = −x −2 . |
||||||||
|
|
|
|
= 0, |
|
|
|
|
|
|
|
|
|
|
|
2A −C |
|
|
|
|
|
|
|
||
|
|
Скачано |
|
|
−(x2 + 2) , y′ = c1ex −c2e−x −2x . |
|||||||
|
|
|
y = y + y = c1ex + c2e−x |
|||||||||
|
|
|
При x = 0 |
y(0) = −2, |
′ |
|
|
|||||
|
|
|
y (0)с=1, |
|
|
|||||||
|
|
|
−2 = c1 +c2 − 2; |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 = c1 −c2 , |
|
|
|
|
|
|
|
|
|
|
|
|
откуда c = |
1 , |
c |
= − 1 . |
|
|
||||
|
|
|
|
1 |
2 |
|
2 |
|
|
2 |
|
|
|
|
|
Общее решение НЛДУ имеет вид: y = 12 (ex −e−x )−(x2 + 2). |
|||||||||
3. Если f (x) = Pn (x) , |
α = 0 , то решение y нужно искать в следующем ви- |
|||||||||||
де: |
|
|
|
|
|
|
|
|
|
|
|
|
1) если число «0» не является корнем характеристического уравнения, то y = Qn (x) ;
2) если число «0» является простым корнем характеристического уравнения, то y = xQn (x) ;
3) если число «0» является двукратным корнем характеристического уравнения, то y = x2Qn (x) , где Qn (x) - многочлен n-го порядка с коэффициентами, подлежащими определению.

312
4. Если f (x) = Pn (x)eα x , где Pn (x) - многочлен n-го порядка, то решение y нужно искать в следующем виде в зависимости от значений корней характе-
ристического уравнения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1) |
если |
α |
не |
является |
|
корнем |
|
характеристического |
уравнения, |
то |
|||||||||||||||||
|
|
y = Q (x)eα x , где Q - |
многочлен n-ой степени с неопределенными ко- |
||||||||||||||||||||||||
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
эффициентами, подлежащими определению подстановкой в НЛДУru |
; |
|
|
||||||||||||||||||||||
2) |
если α - простой (однократный) корень характеристического. |
уравнения, |
|||||||||||||||||||||||||
|
|
то y = xQ (x)eα x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3) |
если |
α |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- двукратный |
корень |
|
характеристического |
|
уравнения, |
то |
|||||||||||||||||||||
|
|
y = x2Q (x)eα x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
f (x) = M cos βx + N sin βx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Будем искать частное решение в виде |
|
y = Acos βx + Bsin βx , |
найдем А и В. |
||||||||||||||||||||||||
|
y′ = −Aβ sin βx + Bβ cos βx , |
|
|
y′′ = −Aβ2 cos βx − Bβ2 sin βx . |
Подстановка |
в |
|||||||||||||||||||||
НЛДУ дает: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(−Aβ2 + Bpβ + Aq)cos βx + (−Bβ2 − Apβ + Bq)si β x = M cos β x + N sin β x . |
||||||||||||||||||||||||||
Из системы |
|
A(q − β2 )+ Bpβ = M ; |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
−Apβ + B |
( |
q − β2 |
) |
= N |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
найдем А и В. |
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1). |
Если число iβ |
не являет я корнем характеристического уравнения, |
то |
||||||||||||||||||||||||
|
|
y = Acos βx + Bsin βx ; |
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2). |
Если |
число iβ является |
|
|
|
|
|
|
|
|
|
|
|
|
уравнения, |
то |
|||||||||||
к рнем характеристического |
|||||||||||||||||||||||||||
|
|
y = x(Acos βx + Bsin βx). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решите урав е ие y′′−4 y′+ 4 y = cos x . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
4 − 4 = 2 , y = (c1 +c2 x)e2 x . |
|
|
|
|||||||
|
|
|
|
y′′−4 y′+ 4 y = 0 , k2 −4k + 4 = 0 , k1,2 = 2 ± |
|
|
|
||||||||||||||||||||
|
|
|
|
β =1, |
k1,2 ≠ β : |
y = Acos x + B sin x . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Найдем А и В. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ = −Asin x + B cos x, y′′ = −Acos x − B sin x ; |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
(−Acos x − B sin x)−4(−Asin x + B cos x)+ 4(Acos x + B sin x)= cos x ; |
|
|
|
||||||||||||||||||||
|
|
|
|
(−A −4B + 4A)cos x +(−B + 4A + 4B)sin x = cos x ; |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
3A −4B =1, |
|
|
|
3 |
|
|
|
4 |
|
|
|
3 |
|
4 |
|
|
|
|
|
|
|
||
|
|
|
|
4A +3B = 0, → A |
= |
|
, B |
= − |
|
y |
= |
|
cos x − |
|
sin x |
; |
|
|
|
|
|||||||
|
|
|
|
25 |
25 |
25 |
25 |
|
|
|
|
||||||||||||||||
|
|
|
|
y = (c1 |
+c2 x)e2 x + |
|
3 |
cos x − |
4 |
sin x . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
25 |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Линейные дифференциальные уравнения |
|
|
|
|
|
|
|
|
|
ru |
313 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Найдите решение НЛДУ y′′+ 4 y = cos 2x . |
. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
Решение: |
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
k |
2 |
+ 4 = 0 → k1,2 |
= ±2i . y = y |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
+ y . |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
y = c1 cos 2x +c2 sin 2x . Так как 2i является корнем характеристического |
|||||||||||||||||
|
|
|
|
|
уравнения: |
y = x (Acos 2x + B sin 2x), |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
y′ = 2x (−Asin 2x + B cos 2x)+ Acos 2x + B sin 2x , |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
y′′ = 4x (−Acos 2x − B sin 2x)+ 4(−Asin 2x + B cos 2x). |
|
|
||||||||||||
|
|
|
|
|
Подстановка в уравнение дает: |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
(−4Ax + 4B + 4Ax)cos 2x +(−4Bx − 4A + 4Bx)sin 2x = cos 2x , |
|
|
|||||||||||||
|
|
|
|
|
откуда |
|
4B =1, |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
−4A = 0, |
→ A = 0, |
B = 4 , |
y = |
|
sin 2x |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
||||||||||
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = c cos 2x +c |
sin 2x + |
sin 2x . |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
4 |
|
|
|
|
|
|
|
6. |
|
Если |
f (x) = P (x)eαx cos βx + Q (x)eαx sin βx , то y в зависимости от кор- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
ней характеристического уравнения нужноantigtuискать в виде: |
|
|
|
|||||||||||||||||||
1) |
|
если число |
α +iβ |
не являет я корнем характеристического уравнения, |
|||||||||||||||||||
|
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
то y = Rp |
(x)eαx cos |
βx +Vp |
(x)eαx sin βx , где Rp (x) и Vp (x) - многочлены с |
|||||||||||||||||
|
|
|
неопределенными к эффициентамис |
, степень которых равна наивысшей |
|||||||||||||||||||
|
|
|
степени многочлен в Pn (x) |
и Qm (x) , |
p = max(n,m) ; |
|
|
|
|||||||||||||||
2) |
|
если число α +iβ |
является к рнем характеристического уравнения, то |
||||||||||||||||||||
|
y = x[Rp (x)eαx cos β x +Vp (x)eαx sin βx]. |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
! |
|
Указанный вид ч стного решения сохраняется и в тех случаях, |
когда |
|||||||||||||||||||
|
|
|
один |
из |
|
многочленов |
равен |
нулю, |
т.е. |
f (x) = P (x)eαx |
cos βx |
или |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
f (x) = Q (x)eαx sin βx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть НЛДУ т ково, что его правая часть представляет собой сумму не- |
||||||||||||||||||||
|
Т |
|
|||||||||||||||||||||
|
|
|
с оль их, например, |
двух |
функций y′′+ a1 y′+ a2 y = f1(x) + f2 (x) . |
Тогда |
|||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
если y1 - частное решение y′′+ a1 y′+ a2 y = f1(x) , а y2 - частное решение |
||||||||||||||||||||
|
|
|
y′′+ a1 y′+ a2 y = f2 (x) , |
то |
частное |
|
решение |
исходного НЛДУ |
есть |
||||||||||||||
|
|
|
суперпозиция этих двух: |
y = y1 + y2 . |
|
|
|
|
|
|
|
|
|
||||||||||

314 Лекции 12 - 13
13.3. Таблица 5. Решение НЛДУ y′′+ py′+ qy = f ( x) y = yO.O. + yЧ.Н. = y + y
13.3.1. Метод неопределенных коэффициентов |
|
|
|
ru |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (x) |
|
Корни |
|
|
|
|
Вид |
. |
= y |
|||||||
характеристического |
|
|||||||||||||||
|
yЧ.Н. |
|||||||||||||||
|
|
уравнения |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
1. Pn (x) |
а) 0 – не корень |
|
|
|
y = Qn (x) |
|
|
|
|
|
||||||
б) 0 – корень кратно- |
y = xrQ (x) |
|
|
|
|
|
||||||||||
|
сти r (r =1,2) |
|
|
|
|
n |
|
|
|
|
|
|||||
|
а) α – не корень |
|
|
|
αx |
Qn (x) |
|
|
|
|
|
|||||
2. eαx P (x) |
б) α – корень крат- |
y = e |
|
|
|
|
|
|||||||||
n |
ности r (r =1,2) |
|
|
y = xreαxQn (x) |
|
|
|
|
|
|||||||
|
|
|
|
|
||||||||||||
3. Acos βx + Bsin βx |
а) iβ – не корень |
|
|
y = A1 cos βx + Bsin βx |
||||||||||||
б) iβ – корень |
|
|
|
y = xr (A1 cos βx + B1 sin β x) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
4. P (x)cos βx + |
а) iβ – не корень |
|
|
y = Qk cos βx + Mk sin βx , |
||||||||||||
|
|
r |
|
|
|
|
|
|
||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
sin βx], |
|||
+Rm (x)sin βx |
б) iβ – корень |
|
antigtuy = x [Q cos βx + M |
k |
||||||||||||
|
|
|
|
k |
|
|
|
|
||||||||
|
|
|
k = max(n,m) . |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
||||||||||||
5. eαx[P (x)cos βx + |
а) α +iβ – не корень |
y = eαx[Q cos βx + M |
k |
sin βx], |
||||||||||||
n |
|
|
с |
|
|
|
|
|
k |
|
|
|
|
|||
+Rm (x)sin βx] |
б) α +iβ – к рень |
|
|
y = xreαx[Qk cos βx + Mk sin βx] |
||||||||||||
кратн сти r (r =1,2) |
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||
Здесь Q и M – м огочле ы с еизвестными коэффициентами. |
|
|
|
|
||||||||||||
13.3.2. Метод в ри ций произвольной постоянной |
|
|
|
|
|
|||||||||||
yO.H . = c1(x) y1 + c2 (x) y2 , если y1 и y2 |
- частные решения ОЛДУ и |
|||||||||||||||
Скачано |
c′y |
+ c′y |
2 |
|
= 0, |
|
|
|
|
|
|
|
||||
|
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
||||
′ |
′ |
′ |
′ |
|
= f (x). |
|
|
|
|
|
|
|||||
c1 y1 |
+ c2 y2 |
|
|
|
|
|
|
|
||||||||
13.3.3. Принцип суперпозиции
Если f (x) = f1(x) + f2 (x) +... + fn (x) , то y = y1 + y2 +... + yn .
Линейные дифференциальные уравнения |
315 |
13.4. НЛДУ высших порядков
ции или постоянные. Пусть известно общее решение y = c1 y1 + c2 y2 +... + cn yn
y(n) + a y(n−1) |
+... + a |
n |
y = f (x), a (i =1,2,...,n) , f (x) – непрерывные функ- |
||
1 |
|
i |
. |
ru |
|
|
|
|
|
||
|
y1, y2 ,..., yn и имеют вид: |
|
|
|
|
|
|
antigtu |
|
||||||||||
соответствующего ОЛДУ: |
y |
(n) |
+ a y(n−1) +... + a |
n |
y = 0 . |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
13.4.1. Метод вариации произвольных постоянных |
|
|
|
||||||||||||||||
Т |
Общее решение НЛДУ имеет вид |
|
y = c1(x) y1 + c2 (x) y2 +... + cn (x) yn , где |
||||||||||||||||
|
yi |
(i =1,2,…, n) – частные решения ОЛДУ, а ci = ci (x) (i =1,2,…, n) – |
|||||||||||||||||
|
функции, производные которых удовлетворяют системе уравнений: |
|
|||||||||||||||||
|
|
|
|
|
+ c2′y2 +... + cn′ yn = 0, |
|
|
|
|
|
|||||||||
|
|
c1′y1 |
|
|
|
|
|
||||||||||||
|
|
c1′y1′ + c2′y2′ +... + cn′ yn′ = 0, |
|
|
|
|
|
||||||||||||
|
|
.............................................. |
|
|
|
(*) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
(n−2) |
|
′ |
( −2) |
+ |
|
|
′ |
( |
−2) |
= 0, |
|
||||
|
|
c1 y1 |
|
|
+ c2 y2 |
|
... + c y |
|
|
|
|
||||||||
|
|
|
′ |
(n−1) |
|
|
′ |
( −1) |
|
|
|
′ |
( |
−1) |
|
|
|
||
|
|
c1 y1 |
|
|
+ c2 y2 |
|
+... + cn yn |
|
|
= f (x), |
|
||||||||
|
т.е. |
являются решением |
|
этой |
|
системы |
|
{c1′(x),c2′(x),...,cn′(x)} |
при |
||||||||||
|
∆ =W (y1, y2 ,..., yn )≠ 0 |
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
для |
линейно |
независимых частных решений |
|||||||||||||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
c1(x) = ∫c1′dx + c1, |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
c2 (x) = ∫c2′dx + c2 , |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
............................... |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
∫ |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c (x) = |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
c dx + c . |
|
|
|
|
|
|||||||
|
Доказательство: |
|
|
|
|
|
n |
|
n |
|
|
n |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Продиффере цируем у n раз, учитывая (*): |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
y = c1 y1 + c2 y2 +... + cn yn , |
|
|
|
|||||||||||
|
|
|
|
|
y′ = c1 y1′ + c2 y2′ +... + cn yn′ , |
|
|
|
|||||||||||
|
(ост льные члены равны нулю из первого уравнения системы для ci′ |
(*)). |
|||||||||||||||||
|
|
y(n−1) = c y (n−1) |
+ c y (n−1) +... + c y (n−1) , |
|
|||||||||||||||
|
|
|
|
|
1 1 |
|
|
2 |
2 |
|
|
|
|
n n |
|
||||
|
|
y(n) = c y |
(n) |
+ c y (n) +... + c y |
(n) + f (x) . |
|
|||||||||||||
|
|
|
|
|
1 1 |
|
2 |
2 |
|
|
|
|
n |
n |
|
|
|
|
|
316 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекции 12 - 13 |
|||
|
|
Умножим полученные выражения для производных на коэффициенты ai |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
(i =1,2,...,n) и сложим их почленно. Суммы по вертикальным столбцам |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
равны нулю, так как y1, y2 ,..., yn - |
частные решения ОЛДУ, ненулевыми |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
остаются слагаемые |
y(n) + a y(n−1) |
+... + a |
n |
y = f (x) , |
значит |
|
y |
ru |
- решение |
||||||||||||||||||||||||||||||||||||||
|
|
НЛДУ. |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Найдите решение НЛДУ y′′′+ y′ = |
|
|
1 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1. Найдем частные решения ОЛДУ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y′′′+ y′ = 0 , |
k3 + k = 0 , |
|
|
k1 |
= 0 , |
k2,3 |
= ±i . |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
Значит, |
|
y1 =1 , y2 = cos x, |
y3 = sin x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
2. Установим вид yO.O. = y : y = c1 +c2 cos x +c3 s n x . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
3. Запишем вид yO.H . : y = c1 (x) +c2 (x) cos x +c3 (x)sin x . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
4. Составим систему уравнений для определения ci′(x) : |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+c′ si |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c′ 1+c′ cos x |
x = 0, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−c2′ sin x +c3′ cos x = 0, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−c2′ cos x −c3′ sin x = |
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
cos x |
|
|
|
|
|
|
||||||
|
|
|
Решением этой |
|
и темы являют я: |
c |
′ |
= |
|
|
, |
c |
′ |
= − |
, |
c |
′ |
= −1. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu1 2 |
|
sin x |
|
3 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
5. Найдем c (x) : c (x) = |
|
|
dx |
|
|
|
x |
|
+c |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
= ln |
|
tg |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
i |
1 |
|
|
|
|
с |
|
∫sin x |
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
c2 (x) = |
∫ |
− |
cos x |
|
|
|
|
|
|
|
|
|
sin x |
|
+c2 , c3 (x) = −x +c3 . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
sin x |
dx = −ln |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
6. Запишем решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
(−ln | sin x | +c2 )cos x +(−x + c3 )sin x = |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
y = ln |
tg |
|
+c1 + |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
tg |
x |
|
|
−cos x ln | sin x | −x sin x +c +c |
cos x +c |
sin x. |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
= ln |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
3 |
|
|
|
|
|||||
13. 4.2. Метод |
неопределенных коэффициентов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Частное решение НЛДУ |
|
y может быть найдено методом неопределен- |
|||||||||||||||||||||||||||||||||||||||||||||
ных коэффициентов для некоторых видов функции |
|
f (x) |
в правой части |
||||||||||||||||||||||||||||||||||||||||||||||
уравнения и корней характеристического уравнения его левой части. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Р ссмотрим следующие случаи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
I. |
f (x)= P(x)eαx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1). |
Если α не является корнем характеристического уравнения, то частное |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
решение ищем в виде y = R(x)eαx , гдеR(x) - многочлен с неизвестными коэффициентами, степень которого совпадает со степенью P(x);
|
|
|
yIV − y = x3 |
+1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
|
|
317 |
|
|||
|
Линейные дифференциальные уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2). |
Если α корень кратности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||
|
µ характеристического уравнения, то частное |
|
||||||||||||||||||||||||||||||
|
решение ищем в виде y = xµ R(x)eαx . |
|
|
|
|
antigtu |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Характеристическое уравнение k4 −1 = 0, k4 =1, |
k =1, |
k |
2 |
= −1, k |
3 |
= i, k |
4 |
= −i . |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
Общее решение однородного уравнения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
= C ex +C |
e−x |
+ C cos x + C |
|
sin x . |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
y |
4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правая часть уравнения |
f (x) = x3 +1 имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
P (x)eαx , где n = 3, α = 0 , |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
корни характеристического уравнения не совпадают с α . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Частное решение ищем в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
y = Rn (x)eαx = R3 (x)e0 x = (A0 x3 + A1x2 + A2 x + A3 ), y ' = 3A0 x2 + 2 A1x + A2 , |
|
||||||||||||||||||||||||||
|
|
|
|
|
y " = 6A x + 2 A , y '" = 6A , y |
|
= 0, − A x3 |
− A x2 − A x − A = x3 |
+1. |
|
|
|||||||||||||||||||||
|
|
|
|
|
IV |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
1 |
|
|
|
0 |
|
|
|
|
0 |
|
1 |
|
2 |
|
|
3 |
|
|
|
|
|
|
||
|
|
|
Приравнивая коэффициенты при одинаковых степенях x , получим: |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
−A0 =1, A0 = −1, A1 = 0, A2 = 0, A3 = −1, y = −x −1. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Общее решение: |
y = C ex |
+ C e−x + C cos x + C sin x − x3 −1. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Скачано |
1 |
|
2 |
|
|
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
II. |
|
|
|
αx |
cos |
βx + R |
сαx |
sin βx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
f (x)= P(x)e |
|
(x)e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1). |
Если α +iβ не является к рнем характеристического уравнения, то ча- |
|
|||||||||||||||||||||||||||||
|
стное решение ищем |
в виде |
|
y = u (x)eαx cos βx +υ(x)eαx sin βx , |
где |
|
||||||||||||||||||||||||||
u (x), υ(x)- многочле ы, степе ь которых равна наивысшей степени P(x) и
R(x).
2). Если α +iβ является корнем характеристического уравнения кратности
µ , то частное решение: y = x |
µ |
αx |
cos βx +υ |
αx |
|
|
|
|
|
|
|
|
|||||||
u (x)e |
|
(x)e |
sin βx . |
|
|
|
|
|
|||||||||||
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
− y = 6sin x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
IV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Х р ктеристическое уравнение: k4 −1 = 0 , k =1, k |
2 |
= −1, |
k |
3 |
= i, k |
4 |
= −i . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
Общее решение однородного уравнения |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
= C ex +C |
e−x |
+ C cos x + C |
|
sin x , |
f (x) = 6sin x |
|
|
|
||||||
|
|
|
|
y |
4 |
|
|
|
|||||||||||
|
1 |
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||
|
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
318 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
Лекции 12 - 13 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
f (x) = P (x)eαx cos β x + R (x)eαx sin β x, P (x) = 0, e0 x =1, α = 0, β =1 , |
|
||||||||||||||||||||
|
|
|
|
|
|
|
R0 (x) = 6, α +iβ = 0 + i 1 = i |
|
|
|
|
|
|
k3 |
. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
совпадает с корнем |
→ решение ищем в |
|
|||||||||||||||||||
|
|
|
|
|
|
|
виде: |
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
||||||
|
|
|
|
( n) |
|
|
|
|
( n-1) |
|
|
( n-2 ) |
|
|
|
|
|
sin x + xB0 cos x , |
|
||||||||||
|
|
|
|
|
|
|
y = x (A0 cos x + B0 |
sin x), |
y ' = |
A0 cos x − A0 x sin x + B0 |
|
||||||||||||||||||
|
|
|
|
|
|
|
y " = −2 A0 sin x + 2B0 cos x − A0 x cos x − B0 x sin x , |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
y '" = −3A0 cos x + A0 x sin x − 3B0 sin x − B0 x cos x , |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
y |
IV |
= 4 A sin x + A x cos x − 4B cos x + B x sin x . |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подстановка этих значений в исходное уравнение дает |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 A0 sin x − 4B0 cos x = 6s n x, |
, |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
откуда |
4A = 6, |
A = 6 = |
3 , B = 0 |
и |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
4 |
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
y = x 3 cos x, y = C ex |
+C e−x + C cos x +C |
|
sin x + 3 x cos x |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
2 |
3 |
4 |
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
13.5. Таблица 6. Решение НЛДУ n-го порядка |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
y |
|
+ a1 y |
|
|
+ a2 y |
|
|
+ ...+ an y = f ( x), |
yO.H. = yO.O. + yЧ.Н. |
|
||||||||||||||||
|
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
13.5.1. Метод неопределенных кс |
эффициентов |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Корни |
|
|
|
|
|
Вид частного |
|
||||||
|
|
|
Вид правой части |
|
характеристического |
|
|
|
|
решения |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнения |
|
|
|
|
|
|
|
|
|
|||||
|
1. |
f (x) = Pn (x) - |
|
|
|
|
) число 0 не является |
|
y = Qn (x) |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
корнем |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
много лен степени n |
|
б) число 0 является |
|
y = xrQn (x) |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
корнем кратности r |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
а) число α не является |
|
y = eαxQn (x) |
|
|
|
|
||||||||||
|
|
|
|
αx |
|
|
|
|
|
|
|
|
корнем |
|
|
|
|
|
|
|
|
|
|||||||
|
2. |
f (x) = e |
|
Pn (x) |
|
|
|
б) число α является |
|
y = xreαxQn (x) |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
корнем кратности r |
|
|
|
|
|
|
|
|
|
||||||

|
|
Линейные дифференциальные уравнения |
|
|
|
|
|
|
|
|
|
|
|
319 |
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
а) число iβ не является |
y = A cos βx + B sin βx |
||||||||||||
|
3. |
f (x) = Acos βx + |
|
корнем |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
||||
|
|
|
|
|
|
y = x ( A1 cos βx + |
|
|
||||||||||||
|
|
|
+Bsin βx |
|
б) число iβ является |
|
|
|
||||||||||||
|
|
|
|
|
+B1 sin βx) |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
корнем кратности r |
ru |
|
|
|
|||||||||
|
|
|
|
|
|
|
а) число iβ не является |
y = Qk cos βx + |
|
|
|
|||||||||
|
4. |
f (x) = Pn (x)cos βx + |
|
корнем |
|
|
|
|
+Mk sin βx., k = max(n,m) |
|||||||||||
|
|
|
+R (x)sin βx |
|
б) число iβ является |
|
y = xr (Q cos βx + |
|||||||||||||
|
|
|
|
m |
|
|
корнем кратности r |
|
|
|
k |
|
|
|
|
|||||
|
|
|
|
|
|
|
+ Mk sin βx) |
|
|
|
||||||||||
|
|
|
|
|
|
|
а) число α +iβ не явля- |
y = eαx[Qk cos βx + |
||||||||||||
|
5. |
f (x) = eαx[Pn (x) |
|
ется корнем |
|
|
|
+Mk sin βx] |
|
|
|
|||||||||
|
|
|
cos βx + Rm (x)sin βx] |
|
б) число α +iβ является |
y = xreαx[Q cos βx + |
||||||||||||||
|
|
|
|
|
|
|
корнем кратности r |
|
|
|
|
k |
|
|
|
|||||
|
|
|
|
|
|
|
+Mk sin βx] |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Здесь Q, R, M - многочлены с неопределенными коэффициентами. |
|
|
|
|||||||||||||||
|
|
13.5.2. Метод вариации произвольной постоянной |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
c1′y1 + c2′y2 +…+ cn′ = 0, |
|
|
|||||||
|
|
|
|
Скачано |
|
|
|
c1′y1′ + c2′y2′ +…+ cn′ = 0, |
|
|
||||||||||
|
|
|
|
(x)yn |
|
|
|
|
|
|
… |
|
|
|
|
|
||||
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
yO.H . = c1 |
(x) y1 + c2 (x) y2 |
+…+ cn |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
с |
|
(n−2) |
|
(n−2) |
|
|
(n−2) |
= 0, |
|
|||
|
|
|
|
|
|
|
|
c1′y1 |
|
+ c2′y2 |
|
+…+ cn′yn |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
(n−1) |
|
(n−1) |
+ |
|
|
(n−1) |
= f (x). |
|||
|
|
|
|
|
|
|
|
|
c1′y1 |
+ c2′y2 |
|
…+ cn′yn |
||||||||
|
|
|
|
|
c1 = ∫c1′dx + c1, c2 = ∫c2′dx + c2 ,…cn = ∫cn′dx + cn . |
|
|
|
|
|
||||||||||
|
|
|
|
Если |
f (x) = f1(x) + f2 (x) +…+ fk (x) , |
то частное решение представляет |
||||||||||||||
|
|
! |
|
|||||||||||||||||
|
|
|
|
сумму ч стных решений, соответствующих каждому слагаемому в пра- |
||||||||||||||||
|
|
|
|
вой асти. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
В результ те изучения материала, изложенного в этих лекциях, |
|
|
|
|
|
|||||||||||
|
|
|
|
студенты должны знать: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
основные понятия и методы решения ОЛДУ и НЛДУ; |
|
|
|
|
|
||||||||||
|
|
|
|
|
специальные методы решения ОЛДУ и НЛДУ |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
с постоянными коэффициентами. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Лекция 14 |
|
. |
ru |
|
|
||
СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ |
|
||
|
|
||
УРАВНЕНИЙ |
|
|
|
|
|
|
|
|
antigtu |
|
|
В лекции рассмотрены системы дифференциальных уравнений (ДУ) и методы их решения. Особое внимание уделено линейным системам с постоянными коэффициентами, которые возникают при решении многих задач механики и электротехники.
14.1. Основные понятия 14.2. Метод исключения неизвестных 14.3. Линейные системы ДУ
14.4. Однородные системы линейных ДУ с постоянными коэффициентами
14.5. Неоднородные системы линейных ДУ с постоянными коэффициентами
|
|
|
|
с |
|
|
|
|
|
О |
|
Система n ДУ первого порядка с n неизвестными функциями x1, x2 ,..., xn |
|||||||
|
|
от одной переменной t вида |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
Скачано |
|
x′ |
= f (t, x ,..., x ), |
|||||
|
|
|
1 |
|
1 |
1 |
n |
||
|
|
′ |
= f2 (t, x1,..., xn ), |
||||||
|
|
|
|
x2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.............................. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
= fn (t, x1,..., xn ), |
|||
|
|
|
|
xn |
|||||
|
|
называется ормаль ой системой обыкновенных ДУ. |
|||||||
|
|
Общим решением системы называется совокупность n функций от t и n |
|||||||
О |
|
||||||||
|
|
произвольных постоянных: |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
x |
= x (t,c ,c ,...,c ), |
|||||
|
|
|
|
1 |
|
1 |
1 |
2 |
n |
|
|
|
x2 = x2 (t,c1,c2 ,...,cn ), |
||||||
|
|
|
.................................. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
= x |
(t,c |
,c |
,...,c ), |
||
|
|
|
|
n |
|
n |
1 |
2 |
n |
оторые удовлетворяют всем уравнениям системы.
! Любая система ДУ может быть приведена к нормальному виду. Пусть, например, система состоит из n уравнений порядка m :
Системы дифференциальных уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
321 |
||||||||||||
|
|
|
|
|
(m) |
|
|
|
′ |
′′ |
(m−1) |
|
′ |
(m−1) |
|
|
′ |
|
(m−1) |
), |
|
||||||||
|
|
|
|
|
x1 |
= f1 |
|
|
|
|
, x2 |
,...,x2 |
, ..., xn |
,...,xn |
|
|
|||||||||||||
|
|
|
|
|
(t,x1 ,x1 ,x1 ,...,x1 |
|
,x2 |
,xn |
. |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
), |
|
||
|
|
|
|
|
(m) |
= f2 |
|
′ |
′′ |
|
(m−1) |
, x2 |
′ |
|
(m−1) |
, ..., xn |
′ |
|
|
(m−1) |
|
||||||||
|
|
|
|
|
x2 |
(t,x1 ,x1 |
,x1 ,...,x1 |
|
,x2 |
,...,x2 |
,xn |
,...,xn |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
. ru |
|
||||||
............... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
.............................. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
(m) |
= f |
|
( |
′ |
′′ |
|
(m−1) |
, x |
′ |
,...,x |
(m−1) |
, ..., x |
,x |
′ |
,...,x |
(m−1) |
) |
|
|||||
|
|
|
|
|
x |
|
n |
t,x ,x ,x ,...,x |
|
|
,x |
2 |
n |
n |
|
|
|||||||||||||
|
|
|
|
|
n |
|
1 1 1 |
1 |
|
2 |
2 |
|
|
n |
|
|
|
|
|
|
|||||||||
|
|
Переобозначим функции: x1,0 |
= x1 , x2 ,0 = x2 , ..., xn ,0 |
= xn и введем допол- |
|||||||||||||||||||||||||
нительные: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
′ |
x1,2 |
|
′′ |
|
|
|
(m−1) |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1,1 = x1 , |
= x1 , ..., x1,m−1 = x1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x2 ,1 = x2′, x2,2 = x2′′, ..., x2,m−1 = x2(m−1), |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
..................................................... |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
xn ,1 = xn′ , xn,2 = x′′, ..., x ,m−1 = x(m−1). |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
В новых обозначениях уравнения системы принимают вид: |
|
|
|
||||||||||||||||||||||||
x′ |
= x |
|
, |
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1,0 |
11, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
′ |
= x1,2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x1,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1′,m−2 = x1,m−1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x1′,m−1 = f1 (t,x1,0 ,x11, ,x1,2 ,...,x1,m−1 ,x2,0 ,x2,1 ,...,x2,m−1 ,...,xn,0 ,xn,1 ,...xn,m−1 ), |
|
|
|
|
|||||||||||||||||||||||||
x2,0 = x2,1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x′ |
= x |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,1 |
2 |
,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
............... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2,m−2 = x2,m−1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x2′,m−1 = f2 (t,x1,0 ,x11, |
,x1,2 ,...,x1,m−1 ,x2,0 ,x2,1 ,...,x2,m−1 ,...,xn,0 ,xn,1 ,...xn,m−1 ), |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
....................................................................................................................... |
|
||||||||||||||||||||||||||||
|
′ |
= xn,1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
xn ,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
′ |
= xn ,2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
xn ,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
............... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn ,m−2 = xn,m−1 , |
|
|
,x1,2 ,...,x1,m−1 ,x2,0 ,x2 ,1 ,...,x2,m−1 ,...,xn,0 ,xn ,1 ,...xn ,m−1 ). |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
xn′,m−1 = f2 (t,x1,0 ,x11, |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вместо системы n уравнений порядка m получена нормальная система из n ×m уравнений.

322 Лекция 14
14.2. Метод исключения неизвестных
Нормальная система n ДУ первого порядка сводится к одному ДУ n-го порядка методом исключения неизвестных. Проиллюстрируем этот метод решения на примерах.
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
= y |
2 |
+sin t, |
|
|
|
|
|
|
|
. |
|
ru |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Найдите решение системы |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
dy = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
dt |
|
|
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продифференцируем первое уравнение: |
d 2 x |
= |
2 |
dy |
y |
+cos t ; |
|
|
|||||||||||||||||||
|
dt |
2 |
dt |
|
|
|||||||||||||||||||||||
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
подставим |
из второго уравнения: |
|
d 2 x |
= x + cos t ; |
|
|
|
|
|
|
|||||||||||||||||
|
dt |
|
dt2 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
получим НЛДУ второго порядка для |
x(t) |
: |
d 2 x |
− x = cos t . |
|
|
|
||||||||||||||||||||
|
|
dt |
2 |
|
|
|
||||||||||||||||||||||
|
Его решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − 1 cos t , |
|
||||||
|
x = x + x , |
k 2 −1 = 0 , k = ±1 , |
|
x = c et |
+c e−t , |
x |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = c et |
|
|
|
|
|
|
|
|
|
||||||
|
|
x = c et +c e−t |
− 1 cos t , |
|
−c e−t |
+ 1 sin t , |
|
|
||||||||||||||||||||
|
|
|
1 |
|
|
2 |
2 |
|
|
|
|
|
dt |
|
1 |
|
|
2 |
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
y2 = dx −sin t = c et −c e−t |
− 1 sin t . |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
antigtu |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
x = c et +c e−t |
− 1 cos t, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
= c et −c e−сt − 1 sin t |
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В качестве примера решим систему уравнений второго порядка. |
|
|||||||||||||||||||||||||||
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2x = y, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решите систему dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
d 2 y |
= x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дв жды продифференцируем первое уравнение |
d 2 y |
= |
d |
4 x |
, |
|
|
||||||||||||||||||||
|
dt |
2 |
dt4 |
|
|
|||||||||||||||||||||||
|
подст вим во второе d 4 x = x , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x(4) − x = 0 , k 4 −1 = 0 , |
k = ±1, k |
3,4 |
= ±i . |
||||||||||||||||||||||||
|
|
|
|
|
|
dt4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = c1et |
+c2e−t |
+c3 cos t +c4 sin t, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Ответ: |
|
|
+c e−t −c cos t −c |
|
sin t. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
y = x′′ = c et |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
1 |
|
|
2 |
3 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

′ |
|
|
|
|
|
|
|
|
ru |
323 |
Системы дифференциальных уравнений |
|
|
|
|
|
|
|
|||
14.3. Линейные системы ДУ |
|
|
|
|
|
. |
|
|
||
Нормальная линейная |
система |
ДУ с |
|
n неизвестными функциями |
||||||
x1, x2 ,..., xn от одной переменной t имеет вид: |
|
|
|
|
|
|
||||
x′ |
= a |
x + a |
x |
antigtu |
|
|
|
|||
+... + a |
x |
+ b |
, |
|
|
|
||||
1 |
11 |
1 12 |
2 |
1n |
n |
1 |
|
|
|
|
x2 = a21x1 + a22 x2 +... + a2n xn + b2 , |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
........................................................... |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
′ |
= an1x1 + an2 x2 |
+... + ann xn + bn , |
|
|
|
|||||
xn |
|
|
|
|||||||
где коэффициенты aik и bi - известные функции t или постоянные, i,k =1,2,...,n .
О Система называется неоднородной, если хотя бы одна из функций bi (t) (i =1,..., n) отлична от нуля для t (a,b) ; в противном случае система на-
зывается однородной.
14.4. Решение линейных однородных систем ДУ с постоянными коэффициентами
x′ |
= a |
x + a |
x |
+... + a |
x , |
1 |
11 |
1 12 |
2 |
1n |
n |
′ |
= a21x1 + a22 x2 |
+... + a2n xn , |
|||
x2 |
|||||
Скачано |
|
|
|
|||
.................................................. |
||||||
|
|
|
|
|
|
|
|
x |
′ |
= a |
x |
+ a x |
+... + a x . |
|
|
n |
|
n1 1 |
сn2 2 |
nn n |
14.4.1. Метод исключения неизвестных
Из уравнений системы, а также из уравнений, получающихся дифференцированием урав е ий, входящих в систему, исключают все неизвестные (n- 1) функции, кроме од ой xk , для которой получают одно ДУ более высокого
порядка: xk (n) + a1xk (n−1) + a2 xk (n−2) +... + an xk = 0 .
Интегрируя это ур внение, находят одну из неизвестных функций, а остальные (n-1) неизвестные функции определяются из исходных уравнений и уравнений, полу ившихся при дифференцировании, без интегрирования.
Рассмотрим однородную систему двух уравнений:
x′ = a11x + a12 y,
y′ = a21x + a22 y,
где x(t), y(t) - искомые функции, а aij - постоянные.

|
324 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекция 14 |
||
|
Покажем, что эта система может быть сведена к ДУ второго порядка для |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 x |
|
dx |
|
|
||
|
функции |
x(t) . Продифференцируем |
первое |
уравнение |
|
dt2 = a11 dt + a12 y′, |
|||||||||||||||||||
|
подставим y |
′ |
из второго уравнения, тогда |
d 2 x |
|
dx |
|
(a21x + |
a22 y) , отку- |
||||||||||||||||
|
|
dt2 |
= a11 dt + a12 |
||||||||||||||||||||||
|
да d 2 x −(a + a ) dx + (a a − a a )x = 0 . |
|
|
|
|
|
|
. |
ru |
|
|
|
|||||||||||||
|
dt2 |
11 |
|
22 |
dt |
11 |
22 |
|
12 21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Это уравнение является ОЛДУ второго порядка с постоянными коэффи- |
||||||||||||||||||||||||
|
циентами, его характеристическое уравнение имеет вид: |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
k 2 − (a + a )k + (a a − a a ) = 0 , |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
11 |
|
|
22 |
|
11 |
22 |
12 |
21 |
|
|
|
|
|
|
|
|
|
а решение x = x(t) |
зависит от корней характеристического уравнения. |
|
|
|||||||||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
dx |
= ax + y, |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдите решение системы: dy |
= −x + |
y, |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
= const. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Перепишем систему в других обозначениях: |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
x′ = ax + y, antigtu |
dy . |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ ay, |
где x′ = |
dx , |
y′ = |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
y′ = −x |
|
|
dt |
|
dt |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
′ |
′ |
, |
|
|
|
|
|
|
|
|
|
|
Продифференцируем первое уравнение x |
= ax |
+ y |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
подставим значение |
y |
′ |
из второго уравнения, |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
с |
k 2 |
+ 2ak + (1 + a2 ) = 0 , |
|
|
|
|
|
|
|
||||
|
|
|
|
тогда x′′−2ax′+(1+ a2 )x = 0 , |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
откуда k = a ±i |
и x(t) = eat (C1 cos t +C2 sin t ). |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
Из первого урав е ия найдем |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
y = x′−ax = aet (C1 cos t +C2 sin t )+ |
|
|
|
|
|||||||||||
|
|
|
|
|
+eat (−C1 sin t +C2 cos t )−aeat (C1 cos t +C2 sin t )= eat (−C1 sin t +C2 cos t ). |
||||||||||||||||||||
|
|
|
|
|
|
x(t) = eat (C1 cos t +C2 sin t ), |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Ответ: |
|
|
|
cos t −C1 sin t ). |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
y(t) = eat (C2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x′ = 3x −2 y, |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Найдите решение системы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Решение: |
|
|
|
|
|
y′ = 3x −4 y. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
′′ |
′ |
−2 y |
′ |
= 3(3x −2 y) −2(3x −4 y) = 3x +2 y = 3x + |
|
′ |
|
′ |
, |
|
||||||||||
|
|
|
|
|
x = 3x |
|
3x − x |
= 6x − x |
|
||||||||||||||||
|
|
|
|
|
|
|
x′′+ x′−6x = 0 , k2 +k −6 = 0 , k1 = 2 , k2 = −3 . |
|
|
|
|
||||||||||||||
|
|
|
Корни действительные, разные. |
y = 3x − x′ = C1 e2t +3C |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
x = C e2t +C e−3t , |
e−3t . |
|
|
|
|
|||||||||||||
|
Скачано |
1 |
|
|
2 |
|
|
2 |
|
2 |
|
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

Системы дифференциальных уравнений |
325 |
14.4.2. Непосредственное решение
Рассмотрим однородную систему трех ЛДУ с постоянными коэффициентами для трех неизвестных функций
Сформулируем некоторые общие свойства таких систем:
x′ = a x + a y + a z, |
. |
ru |
|
|||
|
11 |
12 |
13 |
|
||
|
|
|
(*) |
|||
y′ = a21x + a22 y + a23 z, |
|
|||||
|
|
|
|
|
|
|
z′ = a31x + a32 y + a33 z. |
|
|
|
|||
|
|
|
antigtu |
|
|
|
1. |
Если |
функции |
|
{x, y, z} |
|
являются |
|
решением |
системы, |
то |
функции |
|||||
|
{Cx,Cy,Cz}, где С – любое постоянное число, также являются решением |
|||||||||||||||
|
системы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. |
Если {x1, y1, z1} и {x2 , y2 , z2} - решения системы, то {x1 + x2 , y1 + y2 , z1 + z2} |
|||||||||||||||
|
являются решением системы. |
|
|
|
|
|
|
|
|
|||||||
|
Справедливость этих свойств устанавливается непосредственной под- |
|||||||||||||||
|
становкой в систему. |
|
|
|
|
|
|
|
|
|
{x2 , y2 , z2} и |
|||||
3. |
Из вышеприведенных свойств следует, что если {x1, y1, z1}, |
|||||||||||||||
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
{x3 , y3 , z3} являются решениями системы, то их линейные комбинации |
|||||||||||||||
|
{C1x1 +C2 x2 + C3 x3 ,C1 y1 +C2 y2 +C3 y3 ,C1z1 +C2 z2 + C3 z3} |
также |
являются |
|||||||||||||
|
решением системы. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
Скачано |
|
|
|
и темы (*) в виде: |
x =αekt , |
y = βekt , |
|||||||||
|
Будем искать ненулевые решения |
|||||||||||||||
|
z =γekt |
(**), где α, β,γ |
и k - некоторые числа, которые нужно подоб- |
|||||||||||||
|
рать так, чтобы функции (**) уд влетворяли системе (*). |
|
|
|
||||||||||||
|
Подставляя функции (**) и их производные в систему, получим: |
|||||||||||||||
|
|
kt |
= a11α e |
kt |
+ a12 β |
e |
kt |
+ a13γ e |
kt |
, |
(a − k)α + a |
|
β + a γ = 0, |
|||
|
α ke |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
11 |
12 |
|
13 |
|
|
|
β kekt = a21α ekt + a22 β ekt + a23γ ekt , ↔ a21α + (a22 − k)β + a23γ = 0, |
|||||||||||||||
|
γ kekt |
= a α ekt |
+ a β ekt + a γ ekt |
|
a31α + a32 β + |
(a33 − k)γ = 0. |
||||||||||
|
|
|
31 |
|
32 |
|
|
33 |
|
|
|
|
|
|
|
|
Полу или однородную систему с тремя неизвестными α, β и γ . Для то-
го, чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы определитель системы был равен нулю. Таким образом, число k должно удовлетворять уравнению:
a11 − k |
a12 |
a13 |
|
|
|
||||
a21 |
a22 − k |
a23 |
|
= 0 . |
a31 |
a32 |
a33 − k |
|
|

326 |
ru |
Лекция 14 |
|
Это уравнение называется характеристическим уравнением системы. Оно является уравнением третьего порядка относительно k . Имеет три корня k1, k2 и k3 . Каждому из этих корней соответствует ненулевое решение систе-
мы α1, β1,γ1 ; α2 , β2 ,γ2 ; α3 , β3 ,γ3 , а значит, и ненулевое решение исходной сис- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
x′ |
= x + 2 y, |
|
antigtu |
. |
|
|
|
||||||||||||||||||||
темы дифференциальных уравнений имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
=α1e |
k1t |
, |
y1 = β1e |
k1t |
, z1 |
=γ1e |
k1t |
, |
|
|
|
|
||||||||||||||||
|
|
x1 |
|
|
|
|
||||||||||||||||||||||||||
|
|
x2 =α2ek2t , y2 = β2ek2t , z2 =γ2ek2 , |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
x |
=α |
ek3t , y = |
β |
ek3t , z = |
γ |
3 |
ek3 . |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
3 |
3 |
|
|
|
3 |
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Линейные комбинации этих функций с произвольными коэффициента- |
|||||||||||||||||||||||||||||||
ми: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x |
= C1α1ek1t |
+ C2α2ek2 + C3α3ek3 , |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
= C1β1ek1t + C2 β2ek2t + C3β3ek3t , |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
= C1γ |
|
k t |
|
|
|
|
|
k |
t |
+ C3γ |
3e |
k t |
, |
|
|
|
|
|
|
|
|
|||||||
|
|
z |
1e 1 |
+C2γ2e |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
также будут решением системы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решите систему |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Скачано |
y′ = 4x +3y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Характеристическое уравнение имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
1−k |
|
|
2 |
|
= 0 , k 2 −4k −5 = 0 → k = 5, k |
2 |
= −1. |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
4 3 −k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Кор и характеристического уравнения действительные, разные. |
|
|
||||||||||||||||||||||||||||
|
|
Реше ие ищем в виде: x =αe5t , |
y = β |
e−t . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
При этом x′ = 5αe5t , y′ = −βe−t . Подстановка решения такого вида в ис- |
||||||||||||||||||||||||||||||
|
|
ходную систему дает: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
(1−5)α + 2β = 0, |
→ −4α |
+2β |
= 0 , |
|
β = 2α , коэффициент α ос- |
|||||||||||||||||||||||||
|
|
1) k = 5 : |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
4α +(3 −5)β = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
тается произвольным. Полагая α = C , получим |
|
x = C e5t , y = 2C e5t . |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
|
|
|
(1+1)α + 2β = 0, |
→ 2α + 2β = 0, |
|
β = −α , коэффициент α ос- |
|||||||||||||||||||||||||||
|
|
2) k = −1 : |
|
|
|
|
|
= 0 |
|
|||||||||||||||||||||||
|
|
4α +(3 +1)β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
тается произвольным. При α = C |
: |
x = C e−t |
, |
y |
2 |
= −C e−t . |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
||

Системы дифференциальных уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
327 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Общее решение имеет вид: |
x |
= C1e5t +C2e−t , |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
2C e5t −C |
e−t . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y = |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x′ = y + z, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||
|
|
Решите систему y′ = 3x + z, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z′ = 3x + y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Ищем решение в виде x =αekt , |
y = βekt , z =γekt . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
Система для нахождения неопределенных коэффициентов α, β и γ име- |
||||||||||||||||||||||||||||||
|
|
ет вид: |
|
|
|
|
|
|
|
|
|
k + β +γ = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
−α |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k +γ = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
3α − β |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
3α + β −γ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Характеристическое уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
−k |
1 |
1 |
|
|
= 0 , k3 −7k −6 = 0 , |
k = −1, |
k |
|
= −2 |
, k |
|
= 3 . |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
3 −k |
1 |
2 |
3 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
3 |
1 |
−k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Корни характеристического уравнения действительные, разные. Подста- |
||||||||||||||||||||||||||||||
|
|
вим в систему для нахождения α, βantigtuи γ полученные значения k : |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
α + β +γ = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1) k1 |
= −1: |
3α + β |
+γ = 0, откуда |
α = 0, |
β = −γ , |
|
γ |
- любое |
число; |
|||||||||||||||||||||
|
|
|
|
|
|
|
+γ = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
3α + β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
если γ =1, п лучим |
|
x = 0 , |
y |
= −e−t , z |
= e−t . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) k2 |
= −2 : |
2α + β +γ = 0, |
2α + β = −γ, |
|
|
−γ, |
β =γ , |
|
|
- |
любое |
|||||||||||||||||||
|
|
3α + 2β +γ = 0, |
|
|
|
|
|
|
|
|
|
α = |
|
γ |
||||||||||||||||||
|
|
|
|
|
|
|
+ 2γ = 0, |
3α +2β = −γ, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
3α + β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
число; если γ =1, то |
|
|
x = −e−2t , |
y |
2 |
= e−2t |
, |
z |
2 |
= e−2t . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3) k3 |
|
−3α + β +γ = 0, |
−3α + β = −γ , |
откуда |
β =γ , |
|
|
|
2 |
γ , |
|
|
||||||||||||||||||
|
|
= 3 : 3α −3β +γ = 0, |
|
|
|
|
|
|
|
|
|
α = |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3α −3β = −γ , |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||
|
|
|
|
3α + β −3γ = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
где γ |
- любое число; если γ = 3 , то α = 2, |
|
β = 3, |
γ = 3 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
и x = 2e3t , y = 3e3t , z = 3e3t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3 |
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Общее решение системы принимает вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
x |
= −C2e−2t + 2C3e3t , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
= −C1e−t +C2e−2t +3C3e3t , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
z |
= C e−t |
+C |
e−2t |
+3C e3t . |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|

328 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
|
|
Лекция 14 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x′ = x − y, |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||
|
|
|
Решите систему |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Решение: |
|
|
y′ = x +3y. |
antigtu |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Характеристическое уравнение: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1−k |
−1 |
|
= 0 , k 2 −4k +4 = 0 , k = k |
2 |
= 2 . |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
1 |
3 −k |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Корни характеристического уравнения действительные, равные. |
|
|
|||||||||||||||||||||||||
|
|
|
Решение ищем в виде: x = (α + β t)e2t , |
|
y = (α |
2 |
+ β |
t)e2t . |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Для него x′ = e2t (β1 + 2α1 + 2β1t), |
y′ = e2t (α2 + β2 + β2t) . |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
Подстановка этих выражений в исходную систему дает два равносиль- |
|||||||||||||||||||||||||||
|
|
|
ных уравнения вида 2α1 + β1 + 2β1 |
=α1 + β1 |
−α2 − β2t . |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Приравнивая коэффициенты в этом уравнении, получаем: |
|
β |
|
= −β , |
|||||||||||||||||||||||
|
|
|
|
|
2 |
1 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α2 |
=α1 − β1, |
|||
|
|
|
при этом коэффициенты α1 |
и β1 остаются произвольными. |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
Положим, α1 = C1, β1 = C2 , тогда общее решение имеет вид: |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
с |
|
= (C1 +C2t )e |
2t |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
= −(C1 +C2 |
+C2t )e2t . |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скачано |
|
|
x′ |
= −7x + y, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Решите систему |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Решение: |
|
|
y′ = −x −5y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Характеристическ е уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
−7 −k |
1 |
|
|
= 0, k 2 +12k +37 = 0 , |
k = −6 ±i . |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
−2 |
−5 −k |
|
|
|
|
|
|
|
|
|
1,2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Кор и характеристического уравнения комплексные. Ищем решение в |
|||||||||||||||||||||||||||
|
|
|
виде x =α ekt , |
y = β ekt . |
Возьмем одно из комплексно-сопряженных |
|||||||||||||||||||||||||
|
|
|
зн чений k = −6 + i : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
(−7 +6 −i)α + β = 0, |
|
−α −iα + β = 0, |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2α +(−5 +6 −i)β = 0, |
|
−2α + β −iβ = 0, |
|
|
|
|
|
|||||||||||||||||
|
|
|
уравнения равносильны, β =α(1+i) , α и |
β остаются произвольными, |
||||||||||||||||||||||||||
|
|
|
пусть, например, |
β =1+i , тогда x = e(−6+i)t , |
y = (1+i)e(−6+i)t . |
|
|
|
|
|
||||||||||||||||||||
|
|
|
По формуле Эйлера |
|
e(α+β i)t |
= eα (cos t +i sin t) , |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = e−6t (cos t +i sin t) , |
y = (1+i)e−6t (cos t +i sin t) = |
|
|
|
|
|||||||||||||||||||||

Системы дифференциальных уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
ru |
329 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
= e−6t (cos t −sin t) + ie−6t (cos t +sin t) . |
|
. |
|
|
|
|||||||||||||
|
|
За системы частных решений можно взять отдельно действительные и |
||||||||||||||||||||
|
|
отдельно мнимые части: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x = e−6t cos t , |
x |
= e−6t sin t ; |
|
y |
= e−6t (cos t −sin t) , y |
2 |
= e−6t (cos t +sin t) . |
|||||||||||||
|
1 |
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|||
|
|
Этих функций достаточно, чтобы составить общее решение системы в |
||||||||||||||||||||
|
|
виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x = e |
−6t |
(C1 cos t |
+C2 sin t), |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
y = e−6t [C (cos t −sin t) +C |
(cos +sin |
)]. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x′ = x −5y, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Решите систему |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
y′ = 2x − y. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Характеристическое уравнение |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1−k |
|
−5 |
|
= |
0 , k 2 +9 = 0, k = ±3i . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
−1−k |
|
|
|
|
1,2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Воспользуемся k = 3i . Ищем решение в виде x =αe3it , y = βe3it , подста- |
||||||||||||||||||||
|
|
новка такого решения в исходную систему приводит к системе: |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(1−3i)α −5β = 0, |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скачано |
|
|
|
|
|
|
β +3iβ −2α = 0, |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
поэтому α и β остаются произвольны- |
||||||||||||
|
|
двух равносильных уравнений, |
||||||||||||||||||||
|
|
ми, так как β = |
α |
1−3i |
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
, п л жим, например, |
α = 5 , β = 1 − 3i . |
|
|
|
||||||||||||
|
|
|
|
5 |
|
|
|
|
||||||||||||||
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = 5e3it = 5(cos 3t +i sin 3t) , |
y = (1−3i)e3it |
= (1−3i)(cos 3t +i sin 3t) . |
|
|
||||||||||||||||
|
|
Действитель ая и м имая части этого решения также являются реше- |
||||||||||||||||||||
|
|
ниями исход ой системы, а их линейная комбинация с произвольными |
||||||||||||||||||||
|
|
коэффициент ми является общим решением: |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
x = 5C1 cos 3t +5C2 sin 3t, |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
y |
= C (cos 3t +3sin 3t) +C (sin 3t −3cos 3t). |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
14.4.3. Метод интегрируемых комбинаций |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x′ = f (t, x, y), |
|
|
|
|
|
||||
|
Интегрирование некоторых систем вида |
|
1 |
|
|
осуществляется |
||||||||||||||||
|
|
f2 (t, x, y) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ = |
|
|
|
|
|
||||
путем подбора интегрируемой комбинации, т.е. дифференциального уравнения, являющегося следствием уравнений системы, но уже легко интегрирующегося.

330 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
Лекция 14 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
dx |
= y, |
|
|
|
|
antigtu |
|
|
|
. |
|
|
|
|
|||||||||||||||||||
|
Пример: |
|
Решите систему: dt |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
dy |
= x. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Решение: |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Складывая почленно данные уравнения, получаем |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
d (x + y) = x + y, |
d (x + y) |
= dt, ln | x + y |= +ln C |
, x + y = C et . |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
dt |
|
|
|
|
|
|
|
x + y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Вычитая уравнения, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
d (x − y) = −(x − y) , |
|
d (x − y) |
= −dt , ln | x − y |= −t +ln C |
, |
x − y = C e−t . |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
dt |
|
|
|
|
|
|
|
x − y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + y = C1e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из системы |
|
|
|
|
|
e−t |
получаем решение в виде: |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
x − y = C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
x = 1 (C1et +C2e−t ), |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
с |
|
|
= 1 (C1et −C2e−t ) . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Решите систему: |
|
dx |
= |
dy |
|
|
|
= |
dz |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Скачано |
|
z −1 (z − x)2 |
|
x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
, |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − |
1 |
|
|
|
|
|
||||||
|
|
|
Составим интегрируемые комбинации: |
z −1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d (z − x) |
= |
|
|
|
|
, |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − z |
|
|
(z − x)2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x −1) |
|
= (z −1) |
+ C1 |
, |
|
|
|
|
|
||||||||||||||
|
|
|
(x −1)dx |
= (z −1)dz, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
C2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
(z − x)d (z − x) = −dy, |
|
|
|
|
= |
(z − x)2 |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−y + |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Решением системы является линия пересечения поверхностей, |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
(x −1) |
−(z − |
1) |
= C1, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
з д в емая системой: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
− x)2 = C |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
2 y +(z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x′+ a11x + a12 y = b1 (t), |
|
|
ru |
331 |
|
Системы дифференциальных уравнений |
|
|
|
|
||
14.5. Неоднородные линейные системы ДУ с постоянными |
|
|||||
|
коэффициентами |
|
|
. |
|
|
|
Рассмотрим неоднородную систему: |
antigtu |
|
|
||
|
|
|
|
|||
|
y′+ a21x + a22 y = b2 (t), |
|
|
|
||
где bi (t) - известные функции, aij - постоянные, |
x( ), y( ) - искомые функ- |
|||||
ции. |
Продифференцируем по t первое уравнение: |
x′′+ a11x′+ a12 y′ = b1′, |
|
|||
|
|
|||||
откуда
y′ = b1′− a11x′− x′′ ;
a12
из первого уравнения y = b1 − a11x − x′, подстановка во второе уравнение дает:
a12
b1′− a11x′− x′′ |
+ 21x + |
22 |
b1 |
− 11x − x′ |
= b2 |
, |
|
|
|
||||
a12 |
с |
|
|
12 |
|
|
|
|
|
|
|
x′′+ (a11 + a22 )x′+ (a22a11 − a12a21)x = b1′+ a22b1 − a12b2 - уравнение 2-го порядка с
одной неизвестной функцией x(t) . |
|
Скачано |
x = f1(t,C1,C2 ) , подставляя это вы- |
Интегрируя это уравнение, получаем |
ражение и его производную в первое уравнение, найдем вторую искомую функцию y = f2 (t,C1,C2 ) .
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x′+ 2x + y = sin t, |
|
|
|
|
|
|
|
|
|
Найдите реше ие системы |
|
|
|
|
|
|
|
|
|||
|
|
|
|
y′ = 4x + 2 y +cos t, |
|
|
|
|
|
|
|
|
|
π |
|
π |
|
|
|
|
|
|
|
|
|
|
если x |
= 2, |
y |
=1. |
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
′′ |
′ |
+ y |
′ |
= cos t , |
подставляя в |
|||
|
|
|
|
|||||||||
|
Продифференцируем первое уравнение: x |
+2x |
|
|||||||||
|
′ |
|
−2x |
из первого уравнения, получим x |
′′ |
= −2 sin t . |
||||||
|
него x = sin t − y |
|
||||||||||
|
Х р ктеристическое уравнение k2 = 0 имеет решение k |
= k |
2 |
= 0 . |
||||||||
|
x = x + x , |
x = C1 |
|
|
|
|
|
|
1 |
|
|
|
|
+C2t , x ищем в виде x = A sin t + B cos t , |
|
|
|||||||||
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
тогда x′ = A cos t − B sin t , и x′′ = −Asin t − B cos t = −2 sin t , |
|
|
|||||||||
|
от уда A = 2 , B = 0 , |
x = 2 sin t . |
|
|
|
|
|
|
|
|
||
|
Решение имеет вид: x = C1 +C2t + 2sin t . |
|
|
|
|
|
|
|
|
|||
|
При этом x′ = C2 + 2 cos t и |
|
|
|
|
|
|
|
|
|||
|
y = sin t − x′−2x = sin t −(C2 + 2cos t) −2(C1 +C2t + 2sin t) = |
|||||||||||
332 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
2 2 |
|
|
ru |
Лекция 14 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
= (−2C1 −C2 ) −2C2t −3sin t −2cos t. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Итак, общее решение системы ДУ имеет вид: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
x = C1 +C2t + 2sin t , |
|
y = −2C1 −C2 −2C2t −3sin t −2cos t . |
|
|
|||||||||||||||||||||||
|
|
Найдем частное решение из начальных условий: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
π |
|
= 2, |
C +C |
|
π |
|
antigtu |
|
|
|
π |
|
|
|
|
|
||||||||||
|
|
x |
|
2 |
+ 2 = 2, |
|
+C |
|
= 0, |
|
|
|
|||||||||||||||||
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
||||||
|
|
|
π |
|
= |
1, |
−2C |
|
−C |
2 |
− 2C |
2 |
π −3 |
=1, −2C |
−C.(1 |
+π) = 4, |
|
||||||||||||
|
|
y |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
1 |
|
|
2 |
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
C +C |
2 2 |
|
|
C1 |
= −2π, C2 |
= −4 . |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2C +C |
2 |
(π +1) = −4, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = 2π −4t + 2sin t, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Тогда |
|
|
|
|
+8t −3sin t −2cos . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
y = −4π + 4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
В результате изучения материала, изложенного в этих лекциях, |
|
|
|
|
|
|
||||||||||||||||||||||
|
студенты должны знать: |
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
основные понятия и методы решения произвольных систем ДУ; |
|
|
|
|||||||||||||||||||||||||
|
методы решения однородных и неоднородных систем линейных ДУ |
|
|
||||||||||||||||||||||||||
|
с постоянными коэффициентами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Лекции 15 - 16 |
|
ru |
|
|
|
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ |
||
|
|
|
|
antigtu |
|
Во многих случаях функциональная зависимость не может быть сведена к функции одной переменной и приходится рассматривать функции, зависящие от нескольких аргу-
ментов. Основные особенности анализа |
таких функций удобно рассмотреть на примере |
|
функций двух переменных: этот случай |
легко интерпретируется геометрически. |
и содер- |
жит все основные отличия, возникающие при переходе от одной к нескольким переменным.
15.1. |
Основные понятия |
|
15.2. |
Предел функции двух переменных |
|
15.3. |
Непрерывность функции двух переменных |
|
15.4. |
Частное и полное приращения функции двух переменных |
|
15.5. |
Частные производные первого порядка функции двух переменных |
|
15.6. |
Полный дифференциал функции |
|
15.7. |
Частные производные высших порядков |
|
15.8. |
Дифференциалы высших порядков |
|
15.9. |
Формула Тейлора |
|
15.10. |
Производная сложной функции. Полная производная |
|
15.11. |
|
с |
Инвариантность формы полного первого дифференциала |
||
15.12. |
Производная от функции, заданной неявно |
|
16.1. |
Локальные эк тремумы функции двух переменных |
|
16.2. |
Условный эк тремум. Метод множителей Лагранжа |
|
16.3. |
Наибольшее и наименьшее значения функции в области |
|
Скачано |
|
|
16.4. |
Геометрические приложения функций двух переменных |
|
16.4.1. Производная векторной функции скалярного аргумента 16.4.2. Уравнение касательной к пространственной кривой 16.4.3. Н рмальная плоскость и ее уравнение 16.4.4. Касательная плоскость и нормаль к поверхности
15.1. Основные понятия
О |
Если каждой то ке на плоскости или паре значений двух независимых |
|
переменных вели ин M (x, y) D соответствует определенное число z , |
|
|
|
то говорят, то на множестве D определена функция двух переменных |
|
z = f (x, y) = f (M ) . |
|
Множество точек (x, y) D значений независимых переменных x и y , |
О |
|
|
при оторых функция z имеет определенное действительное значение, |
|
|
|
называется областью определения функции двух переменных. |
334 |
|
|
|
|
|
|
|
ru |
Лекции 15 - 16 |
|
|
|
|
|
|
|
|
||
Например, |
|
|
x, y > 0 ; |
|
. |
|
|
|
|
1) площадь прямоугольника S = xy , |
|
|
|
|
|||||
|
|
|
|
|
|||||
2) объем параллелепипеда V = xyz , |
x, y, z > 0 ; |
|
|
|
|
|
|||
3) дальность полета тела, брошенного под углом α |
к горизонту со скоро- |
||||||||
|
область: x2 + y2 ≤ 4 - внутренностьantigtuкруга с радиусом |
|
|
|
0 2 |
||||
стью υ : l = |
υ2 sin 2α |
|
π |
|
|
|
|
|
|
|
g |
|
2 |
|
y |
|
|
|
|
Геометрически |
область |
определения функ- |
|
|
|
|
M 2 |
||
ции двух переменных может быть изображена на |
|
|
|
L |
|||||
плоскости (x, y) областью D с границей L , точ- |
|
|
D |
|
M1 |
||||
ка M1 D , M1 L – внутренняя, а M2 L – гра- |
0 |
|
|
|
x |
||||
ничная точка области.
О Область определения называется замкнутой, если ей принадлежат все точки границы.
Пример: |
y |
Областью определения функции z = 4 − x2 − y2 |
|
|
|
является множество точек, определяемое неравенст- |
|
x |
|||||||
|
|
|
вом |
4 − x2 − y2 ≥ 0 , и представляет собой замкнутую |
|
|||||||
|
|
|
2 и центром в точке (0,0) , включающую границу об- |
|
|
|||||||
|
|
|
ласти. |
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Областью |
пределения функции z = |
1 |
|
явля- |
y |
|
|||
|
|
|
x2 + y2 |
− 4 |
|
|||||||
|
|
|
|
2 x |
||||||||
|
|
|
ется |
езамк утое м ожество |
x2 + y2 −4 ≥ 0 , которое и |
0 |
||||||
|
|
|
предст вляет собой внешность круга без точек грани- |
|
||||||||
|
|
|
|
|
||||||||
|
|
|
цы. |
|
|
|
|
|
|
|
|
|
|
Геометри еское изображение функции двух |
z |
|
|
|
|||||||
|
|
|
|
|
||||||||
переменных |
z = |
f (x, y) определяет |
|
|
|
M ( x, y, z) |
S |
|||||
|
Функция |
в про- |
|
|||||||||
|
|
|
|
|
||||||||
стр нстве поверхность |
S , проектирующуюся |
|
|
|
y |
|||||||
на плос ость |
Oxy в область определения D . |
|
0 |
|
|
|||||||
|
|
|
|
|||||||||
|
Скачано |
|
|
|
|
|
|
|
||||
x
D
|
Функции нескольких переменных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
ru |
335 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Поверхность, задаваемая ра- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
венством z = |
sin x2 + y2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
x2 + y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
15.2. Предел функции двух переменных |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
Пусть z = f (x, y) , |
|
(x, y) D , M 0 (x0 , y0 ) D . |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
О |
|
Множество точек, удаленных от точки M 0 |
|
не больше, чем на r , называ- |
||||||||||||||||||||||||||||||||||||
|
|
|
ется |
r −окрестностью |
точки |
|
|
|
M 0 , |
|
|
задается |
неравенством |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
(x − x0 )2 |
+ (y − y0 )2 |
< r 2 |
и |
геометрически |
представляет |
открытый круг |
||||||||||||||||||||||||||||||||
|
|
|
радиусом r |
с центром в точке M 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Число A называется пределом функции f (x, y) = f (M ) |
в точке M 0 |
при |
||||||||||||||||||||||||||||||||||||
|
О |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
с |
M 0 |
, если для ε > 0 найдется такое |
r , |
|||||||||||||||||||
|
|
|
стремлении точки |
|
к точке |
||||||||||||||||||||||||||||||||||||
|
|
|
что |
|
f (x, y) − A |
|
< ε |
|
|
|
f (М) − A |
|
< ε |
|
|
при всех ( x, y ), принадлежащих r |
- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
окрестности точки |
M |
0 |
|
|
x − x0 |
|
|
< r , |
|
y − y0 |
|
< r . |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
A = lim f (x, y) = lim |
|
f (M ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
x→x0 |
|
|
|
M →M 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
y→y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
lim |
3x + 4 |
= |
|
|
0 + 4 = |
4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
x2 + y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
x→0 |
−1 |
4 −1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
y→2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Выясните, имеет ли функция z = |
|
2xy |
|
|
предел при x → 0 , |
y → 0 . |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
x2 + y2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Пусть то ка M (x, y) |
стремится к точке M 0 (0,0) . |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
Р ссмотрим изменение x и y вдоль прямой y = kx . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
Получим, что lim z = lim |
|
|
|
2kx2 |
|
|
= |
|
|
2k |
|
|
. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
x2 + k |
2 x2 |
1 |
+ k 2 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
x→0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Результат имеет различные значения в зависимости от выбранного |
k , |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
т.е. зависит от пути приближения к (0,0) , и поэтому функция не имеет |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
предела в точке (0,0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||

336 |
|
|
|
|
|
|
y→y00 |
ru |
Лекции 15 - 16 |
||
|
|
|
|
|
|
|
|
||||
|
15.3. Непрерывность функции двух переменных |
|
|
|
|||||||
|
|
Функция |
f (x, y) называется непрерывной в точке (x 0 , y 0 ) , если пре- |
||||||||
|
О |
||||||||||
|
|
дельное значение этой функции в точке M 0 существует и равно частно- |
|||||||||
|
|
||||||||||
|
функция z = |
|
2xy |
не определена в точкеantigtu(0,0) , которая является точкой |
|||||||
|
|
му значению f (x0 , y0 ) : lim f (x, y) = f (x0 , y0 ) . |
|
|
|
||||||
|
|
|
|
|
|
|
|
x→x |
|
|
|
|
|
Для непрерывности f (M ) в точке M 0 необходимо выполнение. |
следую- |
||||||||
|
щих условий: |
|
|
|
|
|
|
|
|||
|
|
1) |
f (M ) определена в точке M 0 и вблизи нее; |
|
|
|
|||||
|
|
2) |
предел |
f (M ) при стремлении точки M к точке M 0 |
произвольным |
||||||
|
способом; |
|
|
f (M ) = f (M 0 ) . |
|
|
|
||||
|
|
|
3) lim |
|
|
|
|
||||
|
|
|
M →M 0 |
f (M ) , непрерывная в каждой точке области |
D , называется |
||||||
|
О |
Функция |
|||||||||
|
|
непрерывной в этой области. |
|
|
|
||||||
|
|
|
|
|
|||||||
|
|
Функция |
f (M ) |
разрывна в точке M 0 , если не выполняется какое-либо |
|||||||
|
О |
||||||||||
|
|
из условий непрерывности. |
|
|
|
||||||
|
|
|
|
|
|||||||
|
|
Например, |
|
с |
|
|
|
||||
|
|
функция z = x2 + y2 – непрерывна на всей плоскости xОy ; |
|||||||||
|
|
|
|
|
x2 |
+ y2 |
|
|
|
|
|
разрыва. Разрыв не устраним, так как предел функции z |
в точке (0,0) не су- |
Скачано |
|
ществует. |
|
15.4. Частное и п лн е приращения функции двух переменных
Пусть z = f (x, y) , (x, y) D .
О Дадим переме ой x приращение ∆x , оставляя переменную y неизменной, тогда р зность ∆x z = f (x + ∆x, y) − f (x, y) называется частным прир щением f (x, y) по x , а разность ∆y z = f (x, y + ∆y) − f (x, y) – частное приращение z по y . Полное приращение функции z = f (x, y)
равно ∆z = ∆f (x, y) = f (x + ∆x, y + ∆y) − f (x, y) .
Пример:
Для функции z = x y частные приращения равны:
∆x z = (x + ∆x) y − xy = ∆x y ; ∆y z = x ∆y ;
полное приращение равно:
∆z = ( x + ∆x)( y + ∆y) − xy = ∆x y + x ∆y + ∆x ∆y = ∆x z + ∆y z + ∆x ∆y .
Видим, что ∆z ≠ ∆x z + ∆y z .
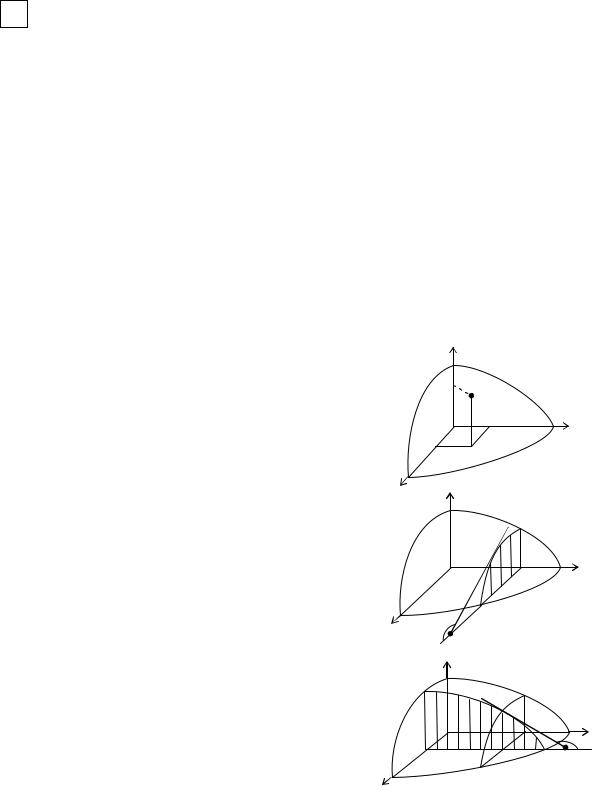
|
|
|
|
∆x→0 |
|
∆x |
|
∆x→0 |
|
|
|
|
∆x |
|
|
|
|
|
|
x |
|
∂x |
|
|
x |
|
|
|
ru∂x |
337 |
|||||
Функции нескольких переменных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
15.5. Частные производные первого порядка функции |
|
|
|
||||||||||||||||||||||||||||||||
|
двух переменных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
О Частной производной по x от функции z = f (x, y) |
называется предел |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∆x z |
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
f |
(x |
+ ∆x, y) − f (x, y) |
|
|
|
′ |
|
∂z |
|
|
′ |
|
|
∂f (x, y) |
|
||||||||||
|
|
|
|
lim |
|
|
|
= lim |
|
|
|
|
|
|
|
|
= |
z |
|
= |
|
= f |
|
(x, y) |
= |
|
|
. |
|||||||
|
Аналогично: |
|
|
|
|
|
|
|
|
|
∆y z |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||||
|
|
′ |
|
|
∂z |
|
|
′ |
|
|
∂f ( x, y ) |
|
|
|
|
|
|
f ( x,y + ∆y ) − f ( x,y ) |
|
||||||||||||||||
|
z |
y |
= |
|
∂y |
= f |
y |
( x, y ) = |
|
∂y |
|
= |
lim |
∆y |
= lim |
|
|
|
|
|
∆y |
|
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∆y→0 |
|
∆y→0 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = x3 sin y + y4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
∂z |
= 3x2 sin y ; |
∂z |
= x3 cos y + 4 y3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
∂x |
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Геометрический смысл частных производных |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Пусть |
z = f (x, y) , M поверхно- |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
x |
|
|
|
z |
|
|
|
|
|
|
|
||||||||||||||||||||
сти S . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
||
Положим y = const . Кривая Гx е ть |
е- |
|
|
|
|
|
|
S |
|
|
M |
|
|
|
|
|
|||||||||||||||||||
чение поверхности |
S пло ко тью, па- |
|
|
|
|
|
|
|
0 |
|
|
|
y |
|
y |
|
|||||||||||||||||||
раллельной плоскости |
Oxz. |
|
x |
|
|||||||
|
Скачано |
|
|
|
|||||||
MK – касательная к крив й |
Гx в т чке |
|
|
||||||||
M ( x, y,z ), а угол, к т рый |
на с став- |
S |
Γx |
||||||||
ляет с осью Ox , равен α . |
|
|
M |
||||||||
∂z |
dz |
|
∂z |
|
|
0 |
y |
||||
∂x |
= |
|
y |
= const , |
∂x |
= tgα . |
|
|
|||
dx |
|
|
|
x |
|
||||||
|
|
|
|
|
|
|
∂z |
α |
K |
||
|
|
|
|
|
|
|
|
z |
|||
Итак, частная производная ∂x численно |
|
S |
|||||||||
равна тангенсу угла наклона касатель- |
|
M |
|||||||||
ной к кривой, получ ющейся в сечении |
0 |
β y |
|||||||||
поверхности |
z = f ( x, y ) |
плоскостью |
x |
||||||||
K ′ |
|||||||||||
|
|
|
|
|
|
∂z |
|
|
|||
y = const . Аналогично |
|
|
|
||||||||
∂y = tgβ . |
x |
|
|||||||||
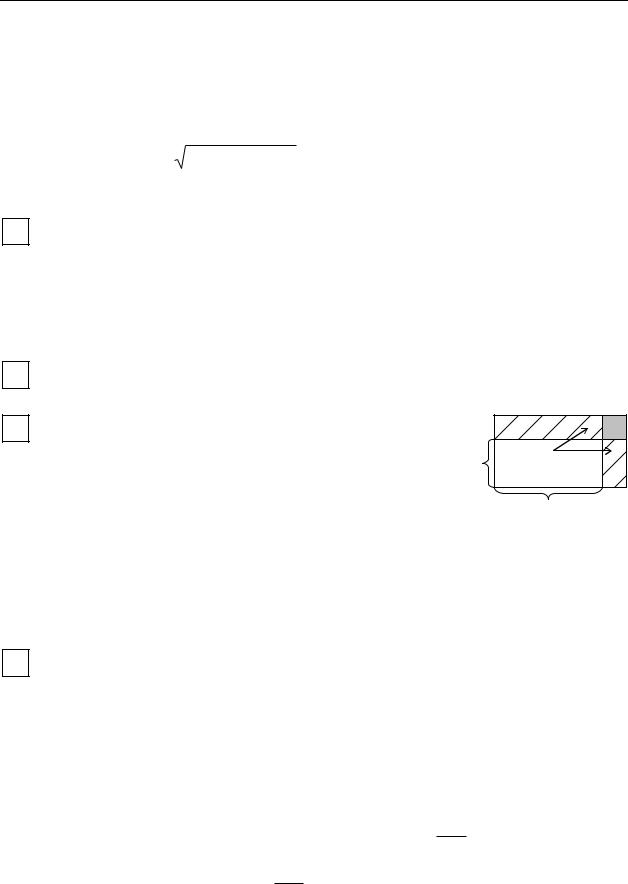
338 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекции 15 - 16 |
|||
15.6. Полный дифференциал функции |
|
|
|
|
|
|
|
||||||||||
|
|
Пусть |
z = f ( x, y ) , |
|
тогда |
полное |
приращение |
функции |
равно |
||||||||
∆z = f (x + ∆x, y + ∆y) − f (x, y) . |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
Рассмотрим две точки: M ( x, y ) и M ( x + ∆x, y + ∆y ) , отстоящие друг от дру- |
|||||||||||||||||
га на расстоянии ρ = |
( ∆x )2 + ( ∆y )2 . |
|
|
|
|
. |
ru |
|
|
|
|||||||
Устремим точку M ′ |
к точке M , при этом ρ → 0 . |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||
О |
|
Если при ρ → 0 можно подобрать не зависящие от ∆x |
и ∆y величины |
||||||||||||||
|
|
A и B так, что выражение ( A ∆x + B ∆y ) будет отличаться от ∆z на |
|||||||||||||||
|
|
величину более высокого порядка малости по сравнению с ρ , то оно на- |
|||||||||||||||
|
|
зывается главной линейной частью полного приращения функции |
|
||||||||||||||
|
|
∆z = A ∆x + B ∆y +γρ , где γ → 0 при ρ → 0 ( ∆x → 0, |
∆y → 0 ). |
|
|
||||||||||||
О |
|
Дифференциалы независимых переменных рав- |
|
|
|
|
|
|
|
||||||||
|
|
ны их приращениям: dx = ∆x , dy = ∆y . |
|
|
|
|
|
|
|
|
|||||||
О |
|
Полным дифференциалом z = f ( x, y ) |
называ- |
|
∆y |
|
∆z |
|
|
|
|||||||
|
|
ется главная линейная часть полного прираще- |
|
y |
|
dz |
|
|
|||||||||
|
|
ния функции: dz = A∆x + B∆y , где |
A, B − const . |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
z = xy |
|
|
antigtu |
|
|
|
x |
|
∆x |
||||
|
|
Например, для |
геометриче ки проиллю- |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
стрируем разницу между ∆z и dz . |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
∆z =( x + ∆x )( y + ∆y ) − xy = y∆x + x∆y + ∆x ∆y = dz + ∆x∆y , |
|
|
|||||||||||||
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
так как dz = ydx + xdy – главная (б льшая) линейная часть приращения функ- |
|||||||||||||||||
ции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
Дифференциал фу кции равен сумме произведений частных производ- |
|||||||||||||||
|
|
ных этой фу кции |
|
а дифференциалы соответствующих независимых |
|||||||||||||
|
|
переменных. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказ тельство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
z = f ( x, y ) . |
По |
определению |
dz = A∆x + B∆y , |
а |
||||||||||
|
|
∆z = A∆x + B∆y +α∆x + β∆y , где α, β – бесконечно малые при ∆x → 0 и |
|||||||||||||||
|
|
∆y → 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Положим ∆y = 0 , тогда ∆x z = A∆x +α∆x , откуда |
∆x z |
= A +α . |
|
|
|
||||||||||
|
|
Устремим ∆x → 0 , тогда lim ∆x z = ∂z = A . |
∆x |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
∆x→0 |
∆x |
∂x |
|
|
|
|
|
|
|
|
|
|
Аналогично: B = ∂z |
, значит, |
dz = |
∂z dx + ∂z dy . |
|
|
|
|
|
|
|
|||||
|
|
|
|
∂y |
|
|
|
|
∂x |
∂y |
|
|
|
|
|
|
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
||||

|
Функции нескольких переменных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
339 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Если |
z = f (x, y) |
|
обладает |
|
непрерывными частными производными |
|||||||||||||||||||||
|
О |
|
|
|||||||||||||||||||||||||
|
|
∂z = f y′(x, y) |
и ∂z |
= f y′(x, y) в данной области, то она дифференцируема |
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
∂x |
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
||||||||
|
|
в этой области. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дифференциала. |
|
|
|
||||||||||
|
|
Геометрический |
|
|
смысл |
|
полного |
|
|
функции |
||||||||||||||||||
|
z = f (x, y) : |
dz в точке (x0 , y0 ) изображается приращением аппликаты точки |
||||||||||||||||||||||||||
|
касательной плоскости, проведенной |
к |
поверхности z = f (x, y) |
в точке |
||||||||||||||||||||||||
|
M 0 (x0 , y0 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Найдите дифференциал функции z = x y . |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
dz = |
∂z dx + |
|
∂z |
dy |
, так как |
∂z |
= yx y−1 , |
∂z |
= x y ln x , |
|
|
|
||||||||||||
|
|
|
|
|
|
∂x |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
∂x |
|
|
∂y |
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|||||
|
|
|
|
то dz = yx y−1dx + x y ln xdy . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
С точностью до бесконечно малых более высокого порядка: ∆z ≈ dz . |
|
|
||||||||||||||||||||||
|
|
|
|
Значит, f (x + ∆x, y + ∆y) ≈ f (x, y) + ∂f (x, y) ∆x + |
∂f (x, y) ∆y . |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
∂x |
|
∂y |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это равенство используется в приближенных вычислениях. |
|
|
|
|||||||||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
Вычислите приближенное значение (2,01)2,02 . |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
Функция имеет вид: z = x y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
Из приближенн го равенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
z(x |
|
+ ∆x, y |
|
|
+ ∆y) ≈ z(x |
, y |
) + |
∂z |
|
|
∆x + |
∂z |
|
|
∆y |
|
|
|
||||||
|
|
|
|
|
0 |
|
0 |
|
|
|
0 |
|
0 |
|
∂x |
( x0 , y0 ) |
|
|
|
|
∂y |
( x , y |
) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|||||
|
|
|
|
при x0 = 2 , |
y0 = 2 , ∆x = 0,01, |
∆y = 0,02 получаем z(x0 , y0 ) = 22 |
= 4 , |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂z = yx y−1 , |
∂z |
|
|
|
= 2 2 = 4 ; |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
∂x |
(2,2) |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
∂z |
= x y |
ln x , |
∂z |
|
|
|
= 22 ln 2 , |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
∂y |
|
(2,2) |
|
|
|
|
|
|
|
|
||
|
|
|
|
полу аем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
(2,01)2,02 ≈ 4 + 4 0,01+ 4ln 2 0,02 = 4(1,01+0,02ln 2) = 4,04 +0,08ln 2 . |
|
|
||||||||||||||||||||||

340 Лекции 15 - 16
15.7. Частные производные высших порядков |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
Частные производные первого порядка от функции двух переменных |
||||||||||||||||
висят |
от порядка |
дифференцированияantigtu, т.е. равны друг другу: |
||||||||||||||
z = f (x, y) , |
равные |
∂z = f x′(x, y) и ∂z |
= |
f y′(x, y) |
, в свою очередь являются |
|||||||||||
|
|
|
|
∂x |
|
∂y |
|
|
|
|
|
|
|
|
|
|
функциями переменных x и y , и от них можно снова находить частныеru |
про- |
|||||||||||||||
изводные второго порядка: |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
∂2 z |
|
∂ ∂z |
|
= f ′′(x, y) ; |
∂2 z |
|
∂ |
|
∂z |
|
= f ′′(x, y) ; |
|
|||
|
∂x |
|
= |
|
|
|
∂y |
|
= |
∂y |
|
∂y |
|
|
||
|
|
2 |
|
|
|
|
xx |
|
2 |
|
|
|
|
|
yy |
|
|
|
∂2 z |
|
∂ ∂z |
′′ |
∂2 z |
|
∂ ∂z |
′′ |
|||
|
|
|
|
= |
|
= |
|
= |
|
= |
||
|
|
|
|
|
|
|
||||||
|
|
∂x∂y |
|
fyx (x, y) ; |
∂y∂x |
|
fxy ( x, y) . |
|||||
|
|
|
∂x ∂y |
|
|
∂y ∂x |
|
|||||
|
Две последние производные по разным переменным называются сме- |
|||||||||||
О |
||||||||||||
|
шанными. |
f (x, y) определена в области D , в которой существуют |
||||||||||
|
||||||||||||
|
Если функция |
|||||||||||
Т |
||||||||||||
|
|
производные |
|
|
|
′ |
|
|
|
|
′ |
|
|
′′ |
, |
′′ |
′′ |
′′ |
и смешанные производные |
′′ |
и |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
f x , |
|
|
fy , |
|
fxx |
f yy , |
fxy , f yx |
fxy |
||||||||||||||||||||||||||||||||
|
|
f yx′′ непрерывны в точке (x0 , y0 ) D , то смешанные производные не за- |
|||||||||||||||||||||||||||||||||||||||||
|
|
f xy′′(x0 , y0 ) = f yx′′(x0 , y0 ) . |
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Запомним эту теорему. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
z = x y , |
x > 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
∂z |
= y xy−1 ; |
|
|
∂2 z |
|
= yx y−1 ln x + x y−1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
∂x |
|
∂y∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
∂z |
= x |
y |
ln x |
; |
|
|
|
∂2 z |
|
|
= yx |
y−1 |
ln x + x |
y−1 |
, значит, |
∂2 z |
|
= |
∂2 z |
. |
|
|
|
||||||||||||||||
|
|
|
|
∂y |
|
|
|
|
∂x∂y |
|
|
∂x∂y |
∂y∂x |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
z = y ln x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
∂z |
= |
|
y |
; |
∂z |
= ln x , |
|
∂2 z |
= |
∂ y |
= − |
y |
, |
∂2 z |
= |
∂ |
(ln x)= 0 , |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
∂x |
|
|
x |
|
∂y |
|
|
|
|
|
|
|
|
|
|
∂x2 |
|
∂x x |
|
|
x2 |
|
∂y2 |
|
∂y |
|
|
|
|
|
|
||||||||
|
|
|
|
∂2 z |
= |
|
∂ y |
= |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
∂y∂x |
|
∂y |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Функции нескольких переменных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
341 |
|||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Вычислите производную восьмого порядка |
|
∂8 z |
|
функции |
ru |
|
|
||||||||||||||||||||||||
|
|
|
|
5 |
∂y |
3 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
. |
|
|
||
|
|
|
|
|
|
|
|
|
|
z = x2 + x + x3 + 2x4 + x7 y9 + y10 |
|
|
|
|||||||||||||||||||||
|
|
|
Последовательно вычисляем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
∂z |
|
7 |
|
8 |
9 ∂2 z |
|
|
|
|
7 7 |
|
|
8 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
∂y = x 9 y +10 y ; ∂y2 = 9 8x y +10 9 y |
|
; |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
∂3 z = 9 8 7x7 y6 |
+10 9 8y |
7 ; |
|
∂4 z |
|
|
= 9 8 7 7x6 y6 ; |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
∂x∂y3 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
∂y3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
∂5 z |
|
= 9 8 7 7 |
6x |
5 |
y |
6 |
; |
|
∂6 z |
|
= 9 |
8 7 7 |
6 5x |
4 |
y |
6 |
; |
|
|
|
|
|||||||||
|
|
|
|
∂x2∂y3 |
|
|
|
∂x3∂y3 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
∂7 z |
|
= 9 8 7 7 6 5 4x3 y6 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
∂x4∂y3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
∂8 z |
|
= 9 8 7 7 |
6 5 4 3x |
2 y |
6 = |
7 9! x2 y6 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
∂x5∂y3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
15.8. Дифференциалы высших порядков |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Пусть z = f (x, y) , |
(x, y) D . |
с |
|
|
|
|
|
antigtu |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
В предположении о суще твовании непрерывных частных производ-
ных второго порядка вычислим дифференциал |
d 2 z второго порядка функции |
|
Скачано |
|
dz при ус- |
z как дифференциал первого порядка от дифференциала функции |
||
ловии, что dz является функцией только x и y . При вычислении дифферен-
циала |
от |
dz |
dx |
и |
dy |
|
считаются |
постоянными, |
при |
вычислении |
||||||||||||
дифференциала от |
∂z |
и ∂z |
приращения x и y берутся равными dx и dy . |
|||||||||||||||||||
|
|
|
|
|
|
∂x |
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
2 |
z |
|
|
|
|
|
∂z |
dx + |
∂z |
|
∂z |
|
|
∂z |
|
||||
|
|
|
= d (dz) = d |
|
|
|
|
dy |
= d dx + d |
dy = |
||||||||||||
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
∂y |
|
∂x |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
||||||
|
|
|
|
|
= ∂2 z dx2 |
+ |
|
∂2 z |
|
dxdy + |
∂2 z dy 2 + |
∂2 z |
dydx = |
|
||||||||
|
|
|
|
|
∂x∂y |
|
|
|
||||||||||||||
|
|
|
|
|
|
∂x2 |
|
|
|
|
|
∂y 2 |
∂y∂x |
|
|
|||||||
|
= |
∂2 z dx2 |
+ |
2 |
|
∂2 z |
|
dxdy + |
∂2 z dy 2 |
, где dx2 |
= (dx)2 , dy 2 |
= (dy)2 . |
||||||||||
|
∂x∂y |
|||||||||||||||||||||
|
|
∂x2 |
|
|
|
|
|
|
∂y 2 |
|
|
|
|
|
|
|||||||
Итак, |
d 2 z = |
∂2 z dx2 |
+ |
2 |
|
∂2 z |
|
dxdy + |
∂2 z dy 2 . |
|
|
|
|
|||||||||
∂x∂y |
|
|
|
|
||||||||||||||||||
|
|
∂x |
2 |
|
|
|
|
|
|
∂y |
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
342 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
Лекции 15 - 16 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Использование символа d = |
|
∂ |
dx + |
|
∂ |
|
dy позволяет записать d 2 z как резуль- |
|||||||||||||||||||||||||||||||||||||||||
|
∂x |
∂y |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
тат действия этого оператора на z в виде: d |
|
|
∂ |
|
|
∂ |
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
2 z = |
|
|
|
|
dx + |
|
|
|
dy |
|
|
z |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Аналогично: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
∂y |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
∂ |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
∂ |
n |
||||
d 3 z = d (d 2 z) = d (d (dz)) |
= |
|
|
|
dx + |
|
|
|
|
dy |
|
|
z , |
d n z = d (d n−1 z) |
= |
|
. |
|
dx + |
|
dy z . |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
∂y |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдите d 2 z , если z = sin xy . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
d 2 z |
= |
∂2 z |
(dx)2 + 2 |
∂2 z |
dxdy + |
|
∂2 z |
(dy)2 , |
|
|
|
|
∂z |
|
= cos xy y , |
|
|
|
|
|
|
∂z |
= cos xy x , |
||||||||||||||||||||||||
|
|
|
∂x∂y |
|
∂y 2 |
|
|
|
|
∂x |
|
|
|
|
|
|
∂y |
|||||||||||||||||||||||||||||||
|
|
|
|
|
∂x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
∂2 z |
= −sin xy y 2 , |
|
|
|
|
|
∂2 z = − si |
xy x 2 , |
|
|
|
∂2 z |
|
= −sin xy xy + cos xy , |
||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
∂x∂y |
|
|||||||||||||||||||||||||||||||||||||
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
d 2 z = −y 2 sin xydx 2 + 2(cos xy − xy sin xy)dxdy − x2 sin xydy 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
15.9. Формула Тейлора |
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
По аналогии с функцией одной переменной формула Тейлора для двух |
||||||||||||||||||||||||||||||||||||||||||||||||
переменных имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Скачано |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
d 2 f ( x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
f ( x, y ) = |
|
f ( x |
, y |
0 |
) + |
|
df ( x , y |
0 |
) + |
|
|
|
, y |
0 |
) + ....+ |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1! |
|
|
|
|
|
0 |
|
2! |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
+ |
|
1 |
d n |
|
f ( x0 , y0 ) + o (ρn (x, y;x0 , y0 )). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Пример: |
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Записать формулу Тейлора для функции z = e xy в окрестности точки P(1,1) |
|||||||||||||||||||||||||||||||||||||||||||||||
|
до чле ов 1-го порядка включительно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Вычисляем ч стные производные f (x, y) = e xy |
в точке (1,1), получаем: |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
xy |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
e |
|
= e + |
1! |
e[( x −1) + ( y −1)] + |
|
2! |
e[( x −1) |
+ ( y − |
1) |
|
+ 2( x −1)( y −1)] |
||||||||||||||||||||||||||||||||||||
|
e[ 1+θ( x−1 )][ 1+θ( y−1 )] . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
15.10. Производная сложной функции. Полная производная
Рассмотрим сложную функцию z = F (u,υ) , где u = ϕ(x, y) , υ =ψ (x, y) ,
т.е. z = F[ϕ(x, y),ψ (x, y)].
Пусть функции F(u,υ) , ϕ(x, y) , ψ (x, y) имеют непрерывные частные производные по всем своим аргументам.
Функции нескольких переменных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
343 |
|||||||||||||||
|
|
Вычислим |
∂z |
и |
∂z . Дадим x приращение ∆x при постоянном y , тогда |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
∂x |
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
ru |
|
|
||||||
u примет значение u + ∆x u , а υ примет значение υ + ∆xυ . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Полное приращение функции z |
|
принимает вид: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∆z = |
|
∂F |
|
∆ |
u + |
∂F |
∆ υ +α∆ |
u + β∆ υ , |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂u |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
∂υ |
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||||||
где α, β – бесконечно малые функции при ∆x → 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
∆z |
= |
|
∂F |
|
∆x u |
+ |
|
∂F ∆xυ |
|
+α |
|
∆x u |
+ β |
|
∆xυ |
. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
∆x |
|
|
|
|
|
|
|
|
|
∂υ ∆x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂u ∆x |
|
|
|
|
|
|
|
|
|
|
|
∆x |
|
|
∆x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
Устремим ∆x к нулю, при этом ∆x u → 0 и ∆xυ → 0 в силу непрерывно- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
сти |
u и υ . |
Так |
|
|
|
|
|
как |
|
|
|
|
lim |
|
∆z |
= |
∂z |
, |
|
|
|
|
lim |
∆x u |
= |
∂u |
, |
lim |
∆xυ |
= ∂υ , |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∆x |
∂x |
|
|
|
|
|
∂x |
∆x |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆x→0 |
|
|
|
|
|
|
|
|
|
|
∆x→0 |
∆x |
|
∆x→0 |
∂x |
|||||||||||||||||||||||
|
limα = lim β = 0 , то ∂z = ∂F ∂u + ∂F ∂υ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
∆x→0 |
∆x→0 |
|
|
|
|
∂x |
|
|
|
|
|
∂u |
|
|
∂x |
|
|
|
∂υ |
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Аналогично: |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
∂F |
|
|
∂u |
|
|
|
∂F |
|
|
|
∂υ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
+ |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
∂u |
|
∂y |
∂υ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
z = ln(u2 +υ), u = ex+y2 , υ = x2 + y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
Вычислим |
∂z |
|
|
и |
∂z |
. |
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
∂z |
|
|
|
2u |
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
= |
|
|
|
, |
|
= |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
∂u |
u2 +υ |
∂υ |
|
u |
2 +υ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
∂u |
|
= ex+y2 |
, |
|
∂u |
|
= 2 yex+y2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
∂x |
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
∂υ |
|
= 2x , |
∂υ |
=1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
∂x |
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(u ex+y2 + x); |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
∂z |
= |
|
2u |
|
|
ex+y2 + |
|
|
|
1 |
|
|
|
|
|
2x = |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
∂x |
u2 + |
υ |
u2 +υ |
|
|
|
u2 +υ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∂z |
= |
|
2u |
|
|
2 yex+y2 |
|
+ |
|
|
|
1 |
|
|
|
|
|
= |
|
|
|
1 |
|
|
(4uyex+y2 +1). |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
∂y |
|
u2 + |
υ |
|
u2 +υ |
u2 |
+υ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Полн я производн я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пусть z = F (x, y) , где y = f (x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
dz |
= |
∂F |
∂x + |
∂F ∂y |
|
, т.е. |
|
dz |
|
= |
∂F |
+ |
∂F |
|
dy |
. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂y ∂x |
|
|
dx |
∂x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
dx |
|
|
∂x ∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y dx |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||

344 |
|
|
|
|
|
|
|
|
|
Лекции 15 - 16 |
Если z = F (x, y) , где x = x(t) , y = y(t) , то |
dz |
= |
∂F dx |
+ |
∂F |
|
dy |
. |
||
|
|
|
|
|
|
|||||
dt |
∂x dt |
|
|
|||||||
|
|
|
∂y dt |
|||||||
15.11. Инвариантность формы полного первого дифференциала |
||||||||||||||||||||
Пусть z = F (u,υ) , где u = u(x, y) , |
|
|
|
|
. |
ru |
||||||||||||||
υ =υ(x, y) . Покажем, что форма пер- |
||||||||||||||||||||
вого дифференциала не меняется и dz = zu′du + zυ′dυ . |
|
|
||||||||||||||||||
Действительно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)dy = |
|
|||
|
|
|
|
|
′ |
′ |
|
|
|
′ ′ |
|
′ |
′ |
|
′ ′ |
′ ′ |
|
|||
|
dz = zx dx |
+ z y dy |
= (zu ux + zυυx )dx + (zu u y |
+ zυυy |
|
|||||||||||||||
|
|
|
|
|
′ |
′ |
′ |
|
|
|
′ |
|
′ |
|
′ |
|
′ |
′ |
|
|
|
|
|
= zu (ux dx + u y dy)+ zυ |
(υx dx +υy dy)= zu du + zυ dυ . |
||||||||||||||||
15.12. Производная от функции, заданной неявно |
|
|||||||||||||||||||
Уравнение |
F (x, y) = 0 |
|
неявно задает |
функцию |
одной |
переменной |
||||||||||||||
y = y(x) . |
|
|
|
|
|
|
|
|
|
|
|
|
antigtu′ |
|
|
|||||
Т Если F(x, y) |
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|||||||
и ее ча тные производные |
Fx (x, y) и Fy (x, y) определены и |
|||||||||||||||||||
непрерывны в некоторой обла ти, |
одержащей точку (x, y) , F (x, y) = 0 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
Fx′(x, y) |
|
|
|
|
|
|
|
||||
и Fy′(x, y) ≠ 0 , то |
y′x = − |
|
|
с |
. |
|
|
|
|
|
|
|||||||||
′ |
(x, y) |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
Fy |
|
|
|
|
|
|
|
||||
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пусть F (x, y) = 0 . Дадим x приращение ∆x , |
тогда |
y примет значение |
||||||||||||||||||
y + ∆y . По условию F (x + ∆x, y + ∆y) = 0 , следовательно, |
полное при- |
|||||||||||||||||||
ращение |
∆F = F (x + ∆x, y + ∆y) − F (x, y) = 0 , |
значит по |
определению |
|||||||||||||||||
∆F : |
∂F |
|
∆x + |
|
∂F |
|
∆y +α∆x + β∆y = 0 , где α, β – бесконечно малые функ- |
|||||||||||||
∂x |
|
∂y |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ции при ∆x, ∆y → 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Тогда |
|
|
|
|
|
∂F |
|
|
∂F |
∆y |
+α + β ∆y = 0 . |
|
|
|||||||
|
|
|
|
|
|
|
|
+ |
|
|
||||||||||
|
|
|
|
|
|
|
|
∂x |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
∂y ∆x |
|
|
∆x |
|
|
|
|||||
Отсюд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Скачано |
|
|
|
∆y |
= − |
∂F |
∂x |
+α |
|
|
|
|||||||||
|
|
|
∂F |
. |
|
|
|
|||||||||||||
|
|
|
∆x |
|
|
∂y |
+ β |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
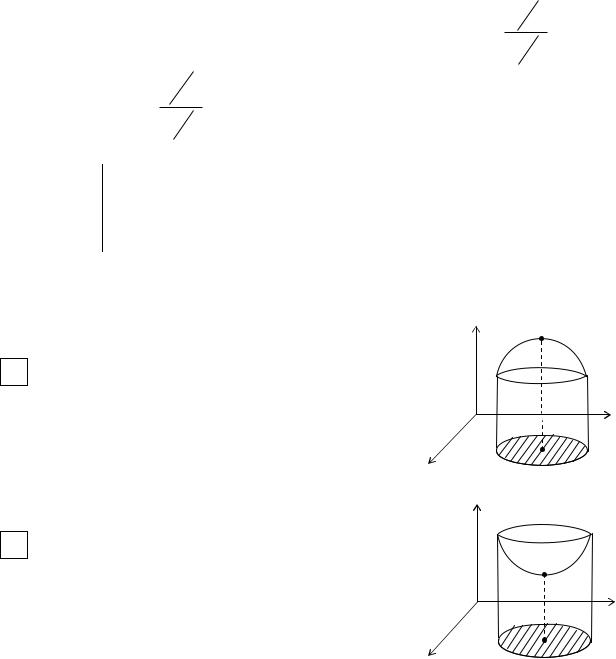
Функции нескольких переменных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
|
345 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
При ∆x → 0 : α, β → 0 ; |
|
∂F |
≠ 0 |
|
по условию, и |
|
. |
|
|
|
|
||||||||||||||||||||||
|
∂y |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂F |
|
|
|
|
antigtu |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
= − |
∂x |
|
= − |
Fx′(x, y) |
|
|
|
|
( ) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
∂F |
|
Fy′(x, y) |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим уравнение F(x, y, z) = 0 . |
|
Оно неявно определяет функцию двух |
|||||||||||||||||||||||||||||||
переменных z(x, y) . Найдем |
|
∂z |
|
и |
∂z . |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
||||
При отыскании |
считаем y |
постоянным, поэтому применима формула ( ) , |
|||||||||||||||||||||||||||||||
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂F ∂x . |
|
|
|
|
если зависимой переменной считать x , а функцией – z : z′x = − |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
∂F ∂y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂F ∂z |
|
|
|
||||||||
Аналогично: z′y |
= − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
∂F ∂z |
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если x |
2 |
+ y |
2 |
+ z |
2 |
|
− R |
2 |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
∂z |
= − |
2x |
= − |
x |
; |
|
∂z |
= − |
2 y |
= − |
y |
. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Скачано |
|
|
|
|
|
2z |
|
|
z |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
∂x |
|
2z |
|
|
|
z |
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
16.1. Локальные экстремумы функции |
z |
|
|
|
|
|
|||||||||||||||||||||||||||
|
О |
двух переме |
|
|
ых |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Функция |
z = f (x, y) |
|
|
имеет |
|
локальный |
|
|
|
|
y |
||||||||||||||||||||
|
|
максимум в |
точке M 0 (x0 , y0 ) , |
|
если для |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
всех то ек (x, y) , |
близких к M 0 |
, выполня- |
x |
|
M0 (x0 , y0 ) |
|
|
||||||||||||||||||||||||
|
|
ется неравенство |
f (x0 , y0 ) > f (x, y) . |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
zmax = f (x0 , y0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
||
|
О z = f (x, y) |
имеет локальный минимум в |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
точ е M 0 (x0 , y0 ) , |
|
|
если |
f (x0 , y0 ) < f (x, y) |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
для всех точек (x, y) , близких к M 0 . |
|
|
|
|
|
y |
|||||||||||||||||||||||||
|
|
zmin = f (x0 , y0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
(x , y ) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
x
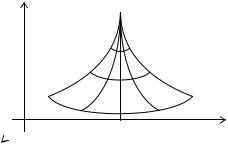
346 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекции 15 - 16 |
|||
|
|
|
Необходимые условия экстремума. В точке экстремума функции двух |
|||||||||||||||||||||||
|
Т |
|
||||||||||||||||||||||||
|
|
|
переменных ее частные производные первого порядка либо равны нулю, |
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||
|
|
|
либо не существуют. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Пусть z = f (x, y) имеет максимальное значение |
f (x0 , y0 ) |
|
|
||||||||||||||||||||
|
|
|
Зафиксируем y = y0 , получим функцию одной переменной z1 = f (x, y0 ) , |
|||||||||||||||||||||||
|
|
|
которая имеет максимум при x = x0 . |
|
. |
ru |
|
|||||||||||||||||||
|
|
|
одной |
переменной |
||||||||||||||||||||||
|
|
|
Из |
теории |
экстремума |
|
|
|
|
|
функции |
|
||||||||||||||
|
|
|
|
dz1 |
|
|
|
= f x′(x0 , y0 ) = 0 или не существует. |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
dx |
|
x=x0 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Аналогично: f y′ = (x0 , y0 ) = 0 или |
|
|
|
. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
В случае минимума доказательство аналогично. В точке экстремума |
|||||||||||||||||||||||
|
|
|
|
M 0 (x0 , y0 ) |
дифференцируемой функции f (x, y) |
производные не суще- |
||||||||||||||||||||
|
|
|
ствуют или равны нулю: |
f |
′(x , y ) = 0; |
|
|
|
|
|||||||||||||||||
|
|
|
|
x |
0 |
0 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
fy′(x0 , y0 ) = 0. |
|
|
|
|
||||||||||
|
О |
|
Точки, |
в которых частные произ- |
|
|
|
|
|
|
||||||||||||||||
|
|
|
водные первого порядка некоторой |
|
z |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
функции равны нулю или не суще- |
antigtu |
|
|
|
|||||||||||||||||||
|
|
|
ствуют, называются критически- |
|
|
|
||||||||||||||||||||
|
|
|
ми. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Геометрический смысл заключает я в |
|
|
M 0 ( x0 , y0 ) |
y |
|||||||||||||||||||||
|
том, что в точке |
M 0 , лежащей выше |
|
x |
|
|||||||||||||||||||||
|
(ниже) всех |
соседних, |
п верхностьс |
|
|
|
|
|
|
|||||||||||||||||
|
z = f (x, y) |
либо имеет г риз нтальную касательную плоскость, либо не име- |
||||||||||||||||||||||||
|
ет никакой касательн й пл ск сти. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Достаточ ые условия экстремума. Пусть в некоторой области, содер- |
|||||||||||||||||||||||
|
Т |
|
||||||||||||||||||||||||
|
|
|
жащей точку M 0 (x0 , y0 ) , функция |
z = f (x, y) имеет непрерывные ча- |
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||
|
|
|
стные производные до второго порядка включительно. |
|
f (x, y) , т.е. |
|||||||||||||||||||||
|
|
|
Пусть |
точка |
M 0 (x0 , y0 ) |
является |
критической точкой |
|||||||||||||||||||
|
|
|
|
∂f (x0 , y0 ) = 0 , |
∂f (x0 , y0 ) = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
∂x |
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Введем обозн чения: |
∂2 f (x0 , y0 ) |
= A, |
∂2 f (x0 , y0 ) |
= B , ∂2 f (x0 , y0 ) = C . |
|||||||||||||||||||
|
|
|
|
∂x2 |
|
|
∂x∂y |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y 2 |
||||
|
|
|
Составим дискриминант ∆ = |
|
A |
B |
|
|
= AC − B 2 . |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
Скачано |
|
|
|
|
B |
C |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Функции нескольких переменных |
ru |
347 |
|
1) если ∆ > 0 , то функция имеет экстремум в точке (x0 , y0 ) , причем это мак-
симум при A < 0 и минимум при A > 0 ; |
|
|
|
|
|
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2) если ∆ < 0 , то экстремума нет; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
3) если ∆ = 0 , то требуется дополнительное исследование |
|
|
|
||||||||||||||||||||||||||||
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
По формуле Тейлора второго порядка |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
f (M ) = |
f (M 0 ) + df (M 0 ) + |
|
1 |
|
d |
2 |
f (M 0 ) + R2 (M ) . |
|
|
|
|||||||||||||||||||||
2! |
|
|
|
|
|||||||||||||||||||||||||||
В критической точке |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
f ′(x0 , y0 ) = f y′(x0 , y0 ) = 0 , |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
df (x0 , y0 ) = f x′(x0 , y0 )dx + f y′(x0 , y0 )dy = 0 , |
|
|
|||||||||||||||||||||||||||
|
|
|
|
f (x, y) − f (x0 , y0 ) = ∆f (x0 , y0 ) |
|
|
|
||||||||||||||||||||||||
и формула Тейлора принимает вид: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
∆f (x |
, y |
) = |
1 |
d 2 f (x |
, y |
) + R (x, y) . |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
2 |
|
|
|
0 |
|
0 |
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Остаточный член R2 (x, y) является бесконечно малой более высокого |
|||||||||||||||||||||||||||||||
порядка, |
|
чем d 2 f (x0 , y0 ) , |
|
|
|
|
поэтому |
|
знак |
∆f (x0 , y0 ) совпадает со знаком |
|||||||||||||||||||||
d 2 f (x , y |
) в окрестности точки (x |
, y |
) . |
|
|
|
|
|
|
|
|||||||||||||||||||||
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
Исследуем знак d 2 f (x0 , y0 ) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
d 2 f (x0 , y0 ) |
= |
∂2 f (x0 , y0 ) |
dx2 + 2 |
∂2 f (x0 , y0 ) |
dxdy + |
||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
Скачано |
|
|
|
|
|
|
|
|
|
∂x2 |
|
|
|
∂x∂y |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
2с |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
∂2 |
f |
(x0 |
, y |
0 ) |
|
dy |
|
Adx |
2 |
|
2Bdxdy + Cdy |
2 |
|
|
||||||||||||||
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
+ |
|
= |
|
||||||||
|
|
|
∂y 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
dx |
2 |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|||||||||
|
|
= dy2 A |
|
|
|
|
+ 2B |
+ C . |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|||||
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Выражение в кв др тных скобках является квадратным трехчленом с дискриминантом D = 4B2 − 4AC = −4∆.
1). Если ∆ > 0 , то D < 0 и знак квадратного трехчлена совпадает со знаком старшего коэффициента A , значит, знак d 2 f (x0 , y0 ) и, следовательно, знак ∆f (x0 , y0 ) совпадает со знаком A , то есть
|
) если A < 0 , |
∆f (x0 , y0 ) < 0 |
и (x0 , y0 ) – точка максимума; |
|
б) если A > 0 , |
∆f (x0 , y0 ) > 0 |
и (x0 , y0 ) – точка минимума. |
2). |
Если ∆ < 0 , то D > 0 и знак квадратного трехчлена меняется в окре- |
||
стности |
точ и (x0 , y0 ) |
и функция |
f (x0 , y0 ) не имеет экстремума в точке |
(x0 , y0 ) . |
|
|
|

348 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
Лекции 15 - 16 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
3). Если ∆ = 0 , то D = 0 и достаточный признак не дает ответа, нужно |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
выяснить сохраняется ли знак разности |
|
|
∆f (x0 , y |
0 ) = f (x, y) − f (x0 |
, y0 ) непо- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
средственно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
antigtu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Схема исследования |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
min |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
f ( x, y) на экстремум: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
1) |
определите критические точки; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
2) проанализируйте выполнение достаточных условий; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3) |
вычислите zэкстр. . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Исследуйте на экстремум функцию z = x2 − xy + y2 +3x −2 y +1. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1) ∂z = 2x − y +3 , |
|
∂z |
|
= −x + 2 y −2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2x − y + 3 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
+ 2 y − 2 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
откуда x0 |
|
= − |
4 |
; |
y0 = |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2) A = |
∂2 z |
|
|
|
|
|
|
|
|
|
= 2 , |
|
B |
= |
|
∂2 z |
|
|
|
|
|
|
|
|
= −1 , C = |
|
∂2 z |
|
|
|
|
|
|
|
|
|
|
= 2 , |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
∂x2 |
|
|
|
|
|
|
|
|
|
∂x∂y |
|
|
|
|
|
|
|
|
|
∂y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
4 |
1 |
|
|
|
|
|
|
|
|
|
|
4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
∆ = AC − B2 = 2 2 −(−1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
Итак, ∆ > 0 , A > 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
; |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
. |
|
|||||||||||||||||||||||||
|
|
|
, значит, − |
3 |
|
|
– точка минимума, z = − |
3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Исслед вать на экстремум функцию z = x |
2 |
y |
2 |
|
x2 |
|
|
|
|
|
y2 |
|
+ xy +1 . |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
+ |
|
+ |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∂z |
= |
|
2xy |
2 |
|
|
+ x |
+ y = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z(0,0) =1. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
= y0 = 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
∂z |
= |
|
2 yx |
2 |
|
|
+ y |
|
+ x = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2). A = |
|
∂2 z |
|
|
|
|
|
=2y2 +1 |
|
|
|
|
|
=1; B = |
∂2 z |
|
|
|
= 4xy +1 |
|
|
|
|
|
|
=1; |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∂x |
2 |
|
(0,0) |
|
(0,0) |
∂x∂y |
|
(0,0) |
(0,0) |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
∂2 z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
C = |
|
|
|
|
|
|
= 2x2 +1 |
|
|
|
|
|
|
|
=1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
∂y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0,0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
(0,0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
∆ = AC − B2 = |
|
|
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Дост точный признак ответа не дает. Исследуем значения z(x, y) . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
x2 |
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
z(x, y) = x |
|
|
y |
|
+ |
|
|
|
+ |
|
|
|
|
|
|
+ xy +1 = |
|
(xy) |
|
+ |
2 |
(x + y) |
|
|
+1 , значит |
z(x, y) >1 , |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
если x ≠ 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
y ≠ 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Получили, что z( x, y) > z(0,0) =1, значит, |
(0,0) |
– точка минимума. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
