Свойства операции умножения матриц:

Добавил:

sava Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Государственный университет — учебно-научно-производственный комплекс (бывш. ОрелГТУ)

Предмет:

Математика

Файл:

Лекции / Курс высшей математики.pdf

Скачиваний:

Добавлен:

13.06.2014

Размер:

9.85 Mб

Скачать

☆

1 / 151 2 3 4 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

ПРЕДИСЛОВИЕ		.	ru

	antigtu
Курс лекций предназначен для студентов технических университетов и
состоит из четырех частей, в которых излагается теоретический материал

курса математики для инженеров.

В первой части излагаются следующие разделы: линейная алгебра, аналитическая геометрия, начала математического анализа (теория пределов и дифференцирование).

Во второй части излагаются следующие разделы: исследование функций, неопределенный и определенный интегралы, дифференциальные уравнения, дифференциальное исчисление функций нескольких переменных

В начале каждой лекции приведены заголовки разделов. В совокупности эти заголовки образуют программу дисциплины и являются базой вопросов для тестовых и экзаменационных заданий. Звездочкой помечены разделы, предназначенные для более глубокого изучения. В конце каждой лекции приведен список ключевых понятий.

В лекциях студент найдет основные определения, формулировки теорем, примеры, демонстрирующие методы решения типичных задач. Если отсутствуют доказательства каких–либо утверждений, то формулировки результатов сопровождаются примерами, разъя няющими их смысл.

	В тексте приняты следующие условные обозначения:
	определение	с
О	определение
Т	теорема
С	следствие
!	замеч ние
	Скачано

Лекции 1-2	.	ru

ОПРЕДЕЛИТЕЛИ И МАТРИЦЫ

В лекциях 1 – 2 излагаются элементы линейной алгебры, в них приведены первоначальные сведения о матрицах и определителях и их применении. Матричное исчисление широко применяется в различных областях математики (решение систем линейных уравнений, векторная алгебра, дифференциальные уравнения, теория вероятности), механики, электротехники, теоретической физики и т.д. Матричное исчисление позволяет в компактной форме получить решение реальных задач, содержащих большое количество переменных.

1.1. Понятие матрицы. Частные виды матриц

1.2.*	Перестановки и подстановки
1.3.* Понятие определителя любого порядка
1.4. Определители второго и третьего порядка
1.5.	Свойства определителей
1.6. Теорема о разложении определителя по строке (столбцу)
1.7. Методы вычисления определителя n-го порядка
	1.7.1. Метод понижения порядка
	1.7.2. Метод сведения к треугольному виду
2.1.		с
	Операции над матрицами
2.2. Обратная матрица. Теорема о существовании левой и правой
	обратной матрицы. Алгоритм нахожденияantigtuобратной матрицы
2.3.	Решение матричных уравнений
Скачано
2.4. Ранг матрицы. Метод окаймляющих миноров.
	Элементарные преобразования матриц
Ниже будут использ ваться с кращенные способы записи сумм и произведений
большого количества элемент в:
	n		n
	∑aj = a1 + a2 +…+ an ,		∏aj = a1 a2 … an .
	j=1		j=1

1.1. Понятие м трицы. Частные виды матриц

Матрицей размерности m ×n называется прямоугольная таблица чисел

aij

a11

a12

...

a1n

...

A =

m,n

= (a )

m,n

2n ,

... ...

...

6		Лекции 1-2
.	ru

где i =1,...,m; j =1,...,n , расположенных в m строках и n столбцах. Числа aij называют элементами матрицы. Числа i, j - индексы элемента матрицы, ука-

зывающие его местоположение: i - номер строки, j - номер столбца. Число

элементов матрицы m ×n определяется как произведение числа строк m на число столбцов n .

Частные виды матриц

О		Нулевой матрицей размерности m ×n называется матрица, все эле-
											0	0	0
											0	0	0
											0	0	0
		менты которой равны нулю, например: =									0	0	0	.
											0	0	0
											0	0	0
		Матрица размерности 1×n			называется матрицей-строкой или просто
О		Матрица размерности 1×n			называется матрицей-строкой или просто
		строкой, например: B = (2			1 7,3)1,3 .
		строкой, например: B = (2			1 7,3)1,3 .
		Матрица размерности m ×1 называется матрицей-столбцом или просто
О
					7			antigtu
					7
		столбцом, например:
		столбцом, например:		C = 3,5		.

					0 3,1
					0 3,1
О		Матрица	называется	квадратной,				если		число			ее	строк	равно числу
		столбцов,	m = n . Число n называется порядком матрицы,												например при
		столбцов,	m = n . Число n называется порядком матрицы,												например при
		n=3:			с
							3	1	2
							0	7	0
					D =		0	7	0	.
							4	5	1
							4	5	1	3,3
		Главной ди гон лью квадратной матрицы называется диагональ, со-
О
		ставленн я из чисел a11,a22 ,...,ann , идущая из левого верхнего угла в пра-

		вый нижний; побочной называется диагональ, идущая из правого верх-
		него угла в левый нижний:
	Скачано													.
	Скачано

Определители и матрицы																	ru	7
Определители и матрицы																		7
	Квадратная матрица называется диагональной, если все элементы,
О
	стоящие выше и ниже главной диагонали, равны нулю:															.
	стоящие выше и ниже главной диагонали, равны нулю:
									6	0		0
											antigtu
							A =		0	2		0	.
								0		0	−11
О	Квадратная матрица называется									треугольной, если все ее элементы,
	расположенные по одну сторону главной диагонали, равны нулю:
			4	1	2
			0	7	5		- верхняя треугольная матрица;
	D =		0	7	5		- верхняя треугольная матрица;
			0	0	1
			0	0	1
		3		0	0
		6		−2	0		- нижняя треугольная матрица.
	D =	6		−2	0		- нижняя треугольная матрица.
		4		−8	1
		4		−8	1
О	Квадратная диагональная матрица с единичными элементами называется
							с
	единичной и обозначается буквой Е.
	Например, единичная матрица 3-го порядка имеет вид:
	Скачано									1	0	0

							E =			0	1	0 .
										0	0
										0	0	1
	Транспонированием матрицы называется преобразование, состоящее в
О
	замене строк столбцами с с хранением их номеров.
	замене строк столбцами с с хранением их номеров.
	Таким образом, строки да						ой матрицы будут в той же последователь-
	ности столбцами тра спо ированной матрицы, и наоборот.
					1	2	3						1	4
					1	2	3		,		T		2 5
			A =		4	5	6		,		A	=	2 5		.
					4	5	6						3	6
													3	6

В слу ае квадратной матрицы транспонирование сводится к повороту м трицы на 180˚ вокруг главной диагонали.

8 Лекции 1-2

1.2. * Перестановки и подстановки							.
							.
О	Перестановкой n символов a1 ,a2 ,...,an называется любое расположение этих сим-
	волов в определенном порядке.					antigtu
	волов в определенном порядке.
	Так как данные n						,n , то изучение пе-
	Так как данные n			символов можно занумеровать числами 1,2,			,n , то изучение пе-
	рестановок любых n символов сводится к изучению перестановок этихruчисел. Число
	всех перестановок из n чисел равно n! =1 2 3 ... n (читается: « n -факториал»).
Пример:
Пример:
		Все перестановки чисел 1, 2, 3 имеют вид: 123, 132, 213, 231, 312, 321.
		Число их 3! = 6.


О	Два числа в перестановке образуют инверсию, если большее число стоит впереди
	меньшего, и образуют порядок, если меньшее число стоит впереди большего.
	Способ подсчета числа инверсий: читаем числа перестановки в порядке их за-
	писи (слева направо), для каждого из чисел считаем, сколько чисел, меньших данно-
	го, стоит правее него, и все полученные числа складываем.
Пример:
Пример:
		В перестановке 528371964 число инверсий равно
					4 + 1 + 5 + 1 + 3 + 2 + 1 = 17.

	Перестановка называет я четной или нечетной, смотря по тому, будет число инвер-
О
	сий в ней четно или нечетно.
	сий в ней четно или нечетно.
	Скачано					местами двух чисел перестановки. Транспози-
О	Транспозицией называется переменас					местами двух чисел перестановки. Транспози-
	ция чисел i и j			б значается через (i, j). От любой перестановки n чисел к любой
	ция чисел i и j
	другой перестан вке тех же чисел можно перейти путем ряда транспозиций, причем
	можно обойтись			е более чем n −1 транспозициями.
Пример:
Пример:
		От перест новки 25134 к перестановке 42513 можно перейти путем че-
		тырех тр нспозиций: (2,4),(2,5),(1,5),(1,3).


О	Подстановкой n исел 1, 2, … n, или подстановкой n-й степени, называется вза-
	имно однозна ное отображение совокупности этих чисел на себя, т.е. такое отобра-
	жение, при котором каждому числу от 1 до n соответствует одно из этих чисел и
	двум р зличным числам всегда соответствуют два различных числа.
	Подст новка записывается двумя строками в общих скобках, причем каждому
	числу верхней строки соответствует стоящее под ним число нижней строки.
			2 1 3 4				→1, 2 → 3 , 3 → 4 ,
	Например,		3 1 4 2		обозначает подстановку, в которой 1		→1, 2 → 3 , 3 → 4 ,
			3 1 4 2

4 → 2 . Иначе можно сказать, что подстановка n-й степени – это соответствие между двумя перестановками n чисел.

Пусть дана квадратная матрица порядка n:

Определители и матрицы											9
В зависимости от расположения чисел в верхней строке одну и ту же подстановку
можно записывать многими способами.
Например, записи	1	2	3	2	3	1	,	3	2	1	обозначают одну и ту же
Например, записи		3	,		1	2	,		3		обозначают одну и ту же
	2	3	1	3	1	2		1	3	2

	подстановку, в которой 1 переходит в 2, 2 в 3, 3 в 1. Каждая подстановка n чисел до-
	пускает n! различных записей. Число различных подстановок n элементов также
	равно n!.	.	ru
	ется число, полученное из элементов этой матрицыantigtuпо формулам:


О

О Подстановка называется четной, если общее число инверсий в обеих ее строках четно, и нечетной, если нечетно. Иначе говоря, подстановка четна, если ее строки име-

ют одинаковую четность, и нечетна, если – противоположную четность.

1.3. * Понятие определителя любого порядка

		a11		a12	...	a1
A = (a )		a		a	...	a
A = (a )		=	21	22	...	2	.
ij	n,n	... ...			...	...
		a		a	...
		n1		n2		nn

Определителем n -го порядка, или определителем матрицы A , при n >1 называ-

a11

a12

...

a1n

aij

n,n =

a21

a22

...

a2n

= ∑(−1)s+t ai1 j1 ai2 j2 ...ain jn ,

...с... ...

...

an1

an2

...

ann

где сумма берется по всем различным между собой подстановкам

...

причем s - число инверсий в верхней, а t

- в нижней строке.

Слаг емые суммы н зываются членами определителя; каждый член опреде-

лителя равен произведению n

элементов матрицы, взятых по одному из каждой

Скачано

строки и каждого столбца, причем это произведение берется со своим знаком, если подстановка индексов етна, и с противоположным, если нечетна.

Определитель первого порядка равен единственному своему элементу. Число всех членов определителя n -го порядка равно n !. Элементы, строки, столбцы и т. д. м трицы A н зыв ются соответственно элементами, строками, столбцами и т. д. определителя A .

Лекции 1-2

1.4. Определители второго и третьего порядка

Определителем квадратной матрицы A второго порядка называется

число, равное det A =

a11

a12

= a a

− a

a .

antigtu

a21

Например,

=1 4 − 2

3 = −2 .

Определителем квадратной матрицы А третьего порядка называется

число, равное

a11

a12

a13

det A =

a21

a22

a23

a31

a32

a33

= a11a22a33 + a12a23a31 + a21a32a13 − a13a22a31 − a21a12a33 − a32a23a11 .

Это выражение получается по правилу треугольников (правилу Саррюса), которое можно пояснить следующей схемой:

Скачано		с	,
	+		-

где элементы определителя изображаются кружками, а соответствующие произведения - отрезками или треугольниками. Знаки «+» и «-» соответствуют знакам слагаемых, входящих в определитель, например,

∆ =	1	0	0	=1 2 1 + 0 1 0 +1 3 0 −0 2 0 −1 3 1−1 1 0 = −1.
∆ =	1	2	1	=1 2 1 + 0 1 0 +1 3 0 −0 2 0 −1 3 1−1 1 0 = −1.
	0	3	1

1.5. Свойства определителей

Сформулированные ниже свойства легко проверяются непосредственным вычислением определителей 2-го или 3-го порядков и остаются справедливыми для определителей порядка n .

Введем необходимые определения.

Определители и матрицы					11
	Суммой нескольких строк одинаковой длины называется строка, каж-
О
			.
	дый элемент которой равен сумме соответствующих элементов данных
	строк.	antigtu
О	Произведением строки на число называется строка, каждый элемент
	которой получен из соответствующего элемента данной строки умноже-

	нием его на данное число.			ru
О	Линейной комбинацией нескольких строк одинаковой длины называ-
	ется строка, равная сумме произведений данных строк на некоторые

	числа, называемые коэффициентами этой линейной комбинации. Если
	одна строка является линейной комбинацией других, то говорят, что она
	линейно выражается через	эти строки. Например, равенство

(1, −1, −3, −5)= 3(1,1,1,1)− 2(1, 2,3, 4) означает, что первая строка является линейной комбинацией двух других.

1˚. При транспонировании определителя его значение не меняется. Свойство 1˚ устанавливает полное равноправие строк и столбцов определителя |A|. Иначе говоря, свойства определителей, доказанные для строк, верны и для столбцов, и наоборот.

2˚. При перестановке местами двух любых строк (столбцов) определитель меняет знак.

3˚. Определитель, имеющий две одинаковые строки (столбца), равен 0.

Из 2˚: при перестановке	трок ∆ = −∆, ∆ + ∆ = 0 , 2∆ = 0 ∆ = 0 .
Скачано
4˚. Общий множитель любой строки (столбца) можно выносить за знак оп-
ределителя.	с

Это свойство можно сф рмулир вать иначе: умножение всех элементов некоторой строки (ст лбца) пределителя |A| на число k равносильно

умножению определителя		а это число, например,
	2	1	2	= 2	1	1	2
	2	1	2		1	1	2
	4	3	4		2	3	4	.
	6	5	6		3	5	6

5˚. Если все элементы некоторой строки (столбца) определителя |A| равны нулю, то и сам определитель равен нулю. Это свойство вытекает из предыдущего при k = 0.

6˚. Если все элементы одной строки (столбца) определителя пропорциональны соответствующим элементам другой строки (столбца), то он равен нулю.

7˚. Если всякий элемент любой строки (столбца) представляет собой сумму двух слагаемых, определитель равен сумме двух определителей, в пер-

12																			Лекции 1-2
вом из которых в соответствующей строке (столбце) оставлены первые
слагаемые, а во втором – вторые, например,																.		ru
	1	2	3		1	2	3			1	2	3		1	2		3
	1	2	3		1	2	3			1	2	3		1	2		3
	4	5	6	=	1 + 3 3 + 2 5 +1				=	1	3	5	+	3	2		1
	7	8	9		7	8	9			7	8	9		7	8		9
								antigtu

8˚. Если к элементам любой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на любое

число, то он не изменится.

Пользуясь свойством 8˚, можно все элементы некоторой строки (столбца) определителя, кроме одного, сделать равными нулю, не меняя при этом величину определителя.

1.6. Теорема о разложении определителя по строке (столбцу)

a11

a12

...

a1n

Рассмотрим определитель n -го порядка

a21

a22

...

a2n

... ... ... ...

an1

an2

...

ann

Минором Мij элемента аij определителя n-го порядка называется опре-

делитель (n-1)

порядка,

полученный

из исходного

вычеркиванием

i-строки и j–ст лбца, на пересечении которых стоит элемент aij.

Н пример, ∆ =

, M13 =

, M32 =

Алгебраическим дополнением Аij элемента аij называется его минор со

зна ом (-1)i+j, где i – номер строки, а j – номер столбца, на пересечении

которых стоит элемент aij,

A = (−1)i+ j M

, например,

Скачано

		n									ru		13
Определители и матрицы													13
A = (−1)1+3 M	13	= (−1)4 M	13	= M	13	,	A = (−1)3+2 M	32	= (−1)5 M	32	= −M	32	.
13	13		13		13		32	32		32		32

Т	Определитель n-го порядка \|A\| численно равен сумме произведений эле-
	antigtu
	ментов любой его строки (столбца) на соответствующие алгебраические

дополнения: .

det A = ∑aij Aij = ai1 Ai1 + ai2 Ai2 +... + ain Ain , i =1,..., n , i=1

det A = ∑aij Aij = a1 j A1 j + a2 j A2 j +... + anj Anj , j =1,..., n . i=1

Эти формулы представляют собой разложение определителя по i-й строке и по j-му столбцу. Например, для определителей третьего порядка разложение по первому столбцу имеет вид:

a11

a12

a13

a21

a22

a23

= a11 A11 + a21 A21 + a31 A31 =

a31

a32

a33

= a

a22

a23

−

a13

= a11a22a33 + a12a23a31 + a21a32a13 − a13a22a31 − a21a12a33 − a32a23a11 .

Скачано

Алгебраическая сумма произведений элементов любой строки (столбца)

определителя |A| на алгебраическое дополнение соответствующих эле-

ментов другой стр ки (ст лбца) равна нулю: ∑Aij akj = 0,k ≠ i .

j=1

Непосредстве

ым вычисле ием показывают,

что этой сумме соответ-

ствует определитель с двумя одинаковыми строками (столбцами).

1.7. Методы вы исления определителя n-го порядка

Определители высшего порядка вычисляются с использованием их свойств двумя способами.

14	ru	Лекции 1-2

1.7.1. Метод понижения порядка

Так как в формуле разложения определителя n-го порядка по строке

(столбцу)

detA= ∑n aij Aij = ai1 Ai1 + ai2 Ai2 + ...+ ain Ain , .

j=1

все алгебраические дополнения являются определителями (n-1)-го порядка, то задача свелась к вычислению n определителей меньшего, (n-1)-го порядка.

Если в некоторой строке исходного определителя много нулей, то именно по ней удобно проводить разложение. Более того, используя свойство 8˚, можно добиться того, что все элементы некоторой строки (столбца), кроме

одного, станут равны нулю.

1.7.2. Метод сведения к треугольному виду

Используя свойства 1˚– 8˚, добиваются такой структуры определителя,

при которой все его элементы, стоящие выше (ниже) главной диагонали, равны нулю, т.е. определитель имеет треугольную форму и численно равен произведению элементов, стоящих на главной диагонали:

antigtu

				a11		a12					...			1n
											с							n
		A	=	0		a22					...			2n	= ∏aii =a11 a22 ... ann .
				... ... ... ...													i	=1
				0			0				...			ann			i	=1
Скачано
Пример:
	Вычислить					пределитель ∆ =										1		0			0	двумя способами.
																1		0			0
																1		2			1
																0		3			1
	1). Разложим определитель по первой строке:
			∆ =1 (−1)1+1						2 1				+ 0 (−1)1+2							1 1		+ 0 (−1)1+3		1 2			= 2 −3 = −1.
			∆ =1 (−1)1+1						2 1				+ 0 (−1)1+2							1 1		+ 0 (−1)1+3		1 2			= 2 −3 = −1.
									3		1									0	1			0	3
	2). Приведем определитель к треугольному виду:
					1		0	0				1		0	0				1		0	0				1
					1		0	0				1		0	0				1		0	0

					1 2 1					=		0 2 1					=		0 2			1	=1 2		−			= −1.
					1 2 1					=		0 2 1					=		0 2			1	=1 2		−			= −1.
					0		3	1				0		3	1				0		0	− 0,5				2
					0		3	1				0		3	1				0		0	− 0,5

Определители и матрицы

2.1. Операции над матрицами

Две матрицы

A = (aij )

и B = (bij

)

m,n

равны, A = B , если равны их размер-

m,n

Свойства операции умножения на чи лоantigtu:

aij = bij ,

ности

все

их

соответствующие

элементы совпадают,

i =1,...,m;

j =1,...,n .

Суммой двух матриц A = (aij )

m,n

и B = (bij )

m,n

одинаковой размерности m ×n

называется матрица

C = (cij )

C = A + B ,

все элементы которой равны

m,n

cij = aij + bij ,

i =1,..., m;

j =1,..., n .

Свойства операции сложения:

1˚. A + B = B + A .

2˚. A + B +C = (A + B) +C .

3˚. A + = A .

4˚. A + (−A) = .

Произведением матрицы A = (

ij )

на число α называется матрица

B = (bij )

m,n

B =α A,

все

элементы

которой

равны

bij =αaij ,

i =1,...,m;

j =1,...,n .

Скачано

5˚. (α β)A =α(β A) .

6˚. α( A + B) =α A +αB .

7˚. (α + β) A =α A + β A .

8˚. 0 A = ; 1 A = A .

Для доказательства свойств 1˚-8˚ достаточно воспользоваться соответст-

вующими определе иями.

Операция умножения двух матриц вводится только для случая, когда

число столбцов первой м трицы равно числу строк второй матрицы.

Произведением матрицы A = (ail )m,n размерности (m ×n)

на матрицу

B = (blj )n,k

размерности

(n ×k )

называется матрица

C = (cij )

= A B

m,k

р змерности (m ×k ), элементы которой вычисляются по формуле:

cij

= ∑ail

blj

= ai1 b1 j + ai2 b2 j

+... + ail

blj i =1,..., m ,

j =1,...,k .

l=1

16		Лекции 1-2
.	ru

Иначе: элемент, стоящий на пересечении i-й строки и j-го столбца матрицы произведения cij , равен сумме произведений элементов i-й строки

матрицы А на соответствующие элементы j-го столбца матрицы В.

Пример:								antigtu
								antigtu

	1	3	1			9	10		. Найти C = A		B .
	Дано: A =		, B =			2			. Найти C = A		B .
	2	4	0			2		1
	c11 =1 1+3 0 =1,					c12 =1 9 +3 2 =15 ,					c13 =1 10 +3 1 =13 ,
	c21 = 2 1+ 4 0 = 2 ,					c22 = 2 9 + 4 2 = 26 ,					c23 = 2 10 + 4 1 = 24 .
	1	15	13
	C =	26	.
	2	26	24
Свойства операции умножения матриц:
			с
	9˚. (A× B)×C= A×( B× C) (A× B)× C= A×( B× C).
	10˚. (A+ B)× C = A× C+ B× C.
	11˚. A×( B + C)= A× B+ A× C.
	12˚. A×E=E× A= A.
Скачано
	13˚. A× = × A = .
	14˚. (A×B)			T	= B		T		T	.
	14˚. (A×B)				= B			× A		.

15˚. det(A× B) = det A×det B .

Для доказательства свойств 9˚-14˚ достаточно воспользоваться определениями операций ад матрицами.

О Матрицы A и B н зыв ются перестановочными (коммутирующими),

если A×B=B×A. В общем случае произведение матриц не коммутативно, A×B≠B×A.

Определители и матрицы

2.2. Обратная матрица. Теорема о существовании левой и правой обратной матрицы.

Алгоритм нахождения обратной матрицы

Квадратная матрица A n–го порядка называется вырожденной, если оп-

ределитель этой матрицы равен нулю,

= 0

, и невырожденнойru

, если

≠ 0 .

Матрица А-1 называется обратной матрицей для некоторой квадратной

матрицы А, если выполняется соотношение: A× A−1 = A−1 × A = E .

Теорема о существовании и единственности обратной матрицы.

Если матрица A не вырождена, то существует, и притом единст-

венная, обратная матрица A−1 , равная A−1 =

( A )T , где A = (Aij )-

det

присоединенная матрица (матрица, составленная из алгебраических до-

полнений элементов исходной матрицы).

Доказательство:

Пусть дана квадратная матрица порядка n :

по теореме о разложении определителя по строке (столбцу),

			a11			a12		...	a1n
				a
	A = (a )		=	a	21	a antigtu... a
	A = (a )		=		21		22		2n		.
	ij	n,n	... ...					... ...
			a		n1	a	n2	...	a	nn
					n1		n2			nn
1.			с
1.	Доказательство существ вания (необходимость). Пусть существует
A−1 . По определению A−1 A = E . По свойству 15˚ операции умножения
матриц det( A−1 A) = det E ,		det A−1 det A = det E =1 det A ≠ 0 , то есть мат-
рица A не вырожде а.
2.	Доказательство существования (достаточность). Пусть матрица A
не вырождена. Н йдем вид элементов								A−1 , для чего вычислим произве-
дение
	C = A ( A )T = (aij ) (Aij )T ,
	n			n				det A,			i = j
	cij = ∑aik ( AT )kj = ∑aik Ajk							det A,			i = j
	cij = ∑aik ( AT )kj = ∑aik Ajk							=
	k =1			k =1				0, i ≠ j
Скачано

18	т.е.	A ( A )T = det A E .																								ru	Лекции 1-2
18																											Лекции 1-2
		det A				0		...		0				1						0 ...			0
					det A																		.
	откуда C =		0					...		0	= det A 0									1 ...			.			= det A E ,
	откуда C =		0					...		0	= det A 0									1 ...			0			= det A E ,
						...		...		...								.
		...				...		...		...				...				.
			0			0		...		det A				0						0			1
	Так как det A ≠ 0 , A						( A )T		= E и A			−1	1		( A			)		T
													=								.
							det A						=	det A							.
	3.	Доказательство единственности (от противного). Предположим, что
	кроме матрицы A−1 ,					для которой A−1 A = E , существует матрица B , для
	которой также B A = E ,							причем			B ≠ A−1 . Вычтем из одного равенства
	другое:
				A−1 A − B A = E − E = , ( A−1 − B) A =.
	Умножив последнее равенство на A−1												справа, получим:
							( A−1 − B) AA−1 = A−1 = .
	Так как A A−1 = E ,				( A−1 − B)E = , A−1 − B = ,															A−1 = B , что противоре-
	чит B ≠ A−1 . Предположение неверноantigtu, обратная матрица единственна.
	Скачано								с
!	1˚.	(A−1 )−1 = A .
	2˚. (α A)−1 =		1	A−1 .
			α
	3˚. (A× B)−1 = B−1 × A−1 .
	4˚. (A−1 )T = (AT )−1 .
Алгоритм н хождения обратной матрицы:
1.	Находим det A , проверяем det A ≠ 0 .
2.	Находим M ij		- все миноры матрицы A .
3.	Определяем		A = (−1)i+ j M					ij	.
			ij					ij
4.	Строим м трицу алгебраических дополнений																A = (Aij						)	и транспониру-
	ем: ( A )T = (Aji ).
	Делим каждый элемент матрицы на det A : A														−1						1				T
5.																=						( A		)		.
5.																=			det A			( A		)		.

Определители и матрицы

Пример:

Найти матрицу, обратную для матрицы A =

1. det A = 4 − 6 = −2 ≠ 0 .

antigtu

2. M11 = 4, M12 = 3, M 21 = 2, M 22

=1.

3. A11

= 4, A12 = −3, A21

= −2, A22

=1.

−3

)

−2

4. A

, ( A

−2

−3

5. A−1 = −

−2

−3

3 / 2 −0,5

Проверка:

1 2 −2

1 −2 +3 1−1 1 0

= E .

A A−1 =

3 − 2

4 1,5

−0,5

−6 +6

0 1

2.3. Решение матричных уравнений

Если A , B - известные матрицы, а X

– неизвестная, то равенство вида

Скачано

A X = B называется матричным уравнением.

Основные типы матричных уравнений:

A X = B . Матрица A д лжна быть квадратной,

≠ 0. Умножим уравне-

ние на A−1 слева: A−1 A X = A−1B , E X = A−1B ,

X = A−1B .

X A = B . Матрица A долж а быть квадратной,

≠ 0. Умножим уравне-

ние на A−1 спр ва:

X AA−1 = B A−1 X = B A−1 .

≠ 0,

≠ 0 .

A X B = C . М трицы A и B должны быть квадратными,

Умножим на A−1 слева: A−1 A X B = A−1C X B = A−1C . Умножим на

B−1 справа: X B B−1 = A−1C B−1 X = A−1 C B−1 .

Пример:

Решить матричное уравнение:

A X = B ,

B =

где A =

;

Лекции 1-2

X = A

−1

B , A

−1

−2

( A )

−0,5

det

1,5

r (A)= r

(B).

− 2

3 5 −1

−1

−1 −1

antigtu

A−1 B =

X =

− 0,5

1,5

5 9

2.4. Ранг матрицы. Метод окаймляющих миноров.

Элементарные преобразования матриц

Пусть в матрице A размерности (m ×n) выбраны k

строк и k столбцов,

причем k ≤ min (m,n). Тогда элементы,

стоящие на пересечении выбранных

строк и столбцов, образуют квадратную матрицу k -го порядка. Определитель Mk этой матрицы называется минором k -го порядка матрицы A .

О		Рангом матрицы A называется число, равное максимальному порядку
		r отличных от нуля миноров M k этой матрицы:

			с
		r = r (A)= r ng A.
О		Матрицы называются эквивалентными, что обозначается A B , если
		Ранг матрицы A вычи ляет я методом окаймляющих миноров или ме-
	Скачано
тодом элементарных преобразований.
Метод окаймляющих мин р в
		Пусть в матрице A элемент aij ≠ 0 , тогда M1 ≠ 0 и r (A)≥1. Окаймляем

этот элемент элеме тами ( j +1)-го столбца и (i +1)-й строки, получаем минор 2-го порядка:

M2 =	ai, j	ai, j+1	.
	ai+1, j	ai+1, j+1

Если M2 = 0 , то присоединяем другие строки и столбцы, перебирая все возможные миноры 2-го порядка. Если все миноры второго порядка равны нулю, то r (A)=1; если же существует хотя бы один минор 2-го порядка, отличный от нуля, то r (A)≥ 2 .

Выбираем отличный от нуля минор 2-го порядка M2 и окаймляем его

элементами соседних строк и столбцов до минора 3-го порядка и так до тех пор, пока не будет выполнено условие: Mr ≠ 0 , но все Mr+1 = 0 .

Определители и матрицы

Пример:

−1

Найти ранг матрицы A =

− 2

2 .

отбрасывание нулевой

троки ( толбцаantigtu) матрицы.

−1

1 −1

−1 1

M1 =1;

M 2

2 −2

= −2 + 2 = 0 , M

2 =

−2 2

= −2 + 2 = 0 ,

M23 =

2 −2

= 2 + 2 = 4 ≠ 0 ; M 3 =

−1

= 0 r( A) = 2 .

2 − 2 2

−1

Метод элементарных преобразований

К элементарным преобразованиям матрицы относятся следующие:

транспонирование;

перестановка строк (столбцов);

умножение строки (столбца) на число α ≠ 0 ;

прибавление к элементам строки (столбца) матрицы элементов другой

строки, умноженных на некоторое число;

Скачано

Элементарные преобразования матрицы не меняют ее ранга.

Для определения ранга матрицы A методом элементарных преобразова-

ний следует:

Переставить стр ки так, чт бы в верхнем левом углу матрицы был нену-

левой элемент.

Все элементы первого столбца, кроме a11 , обратить в ноль:

...

A =

...

3. Повторить операцию со второй строкой: во втором столбце должен быть ненулевой элемент, после чего все элементы второго столбца, кроме a12

и a22 , обр тить в ноль.

О онч тельно после многократного применения указанной процедуры и отбрасывания нулевых строк преобразованная матрица будет иметь вид:

a11		a12 ...			a1,r−1		a1r	...	a1n
	0	a	22	...	a	2,r−1	a	...	a
			22			2,r−1	2r		2n
A = ... ... ...						...	...	...
	0	0 ...			a	−1,r−1	a	...	a
					r	−1,r−1	r−1,r		r−1,n
	0	0 ...				0	a	...	a
							rr		rn

Тогда ранг матрицы A = r (A) = rang A = rang A.

В результате изучения материала, изложенного в этих лекциях, у студентов должны сформироваться следующие понятия:

	матрица - таблица,
	определитель - число,
	ранг матрицы - число,
	минор,
	алгебраическое дополнение.
Студент должен уметь:		с
	вычислять определители 2-го, 3-го и n -го порядков,
	перемножать матрицы,		antigtu
	находить обратную матрицу,		antigtu
	определять ранг матрицы,
	решать матричные уравнения.
Скачано

Лекции 1-2

Лекция 3 СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

В лекции 3 излагаются элементы теории систем линейных уравнений Системы ли-

ретической физики и т.д. Матричное исчисление позволяет в компактной форме получить решение таких систем. Реальные задачи, содержащие большое количество переменных (десятки и сотни), требуют владения этими методами.

нейных уравнений возникают при решении многих задач механики, электротехники, тео-
antigtu	.	ru

3.1.	Системы m линейных уравнений с n неизвестными.
	Основные определения
3.2.	Системы n линейных уравнений с n неизвестными.
	Матричный метод решения. Правило Крамера. Метод Гаусса
	(метод последовательного исключения переменных)
	3.2.1. Системы n-линейных уравнений с неизвестными
	3.2.2. Правило Крамера
	3.2.3. Метод Гаусса
3.3.	Теорема Кронекера - Капелли
3.4. Однородные системы линейных уравнений
3.5.				с
3.5.	Схема отыскания общего решения системы m уравнений
	с n неизвестными
3.6.* Фундаментальная				и тема решений
Скачано
3.1. Системы m линейных уравнений с n неизвестными.
Основные определения
Рассмотрим систему ли ей ых уравнений (СЛУ), содержащую m урав-
нений и n неизвестных:
		a11x1 + a12 x2 +…+ a1n xn = b1,
		a21x1 + a22 x2 +…+ a2n xn = b2 ,
		…………………………………,					(1)

		a x	+ a x		+…+ a x = b .
		m1 1		m2 2	mn n	m
где aij , i =1,..., m;		j =1,...,n	-	коэффициенты системы, bi , i =1,..., m			- сво-
бодные члены, xj ,		j =1,...,n - неизвестные.
Система может быть записана в матричном виде:						A X = B ,

Лекция 3

a11

a12

...

a1n

где

A = (a

)

...

- основная матрица системы,

m,n

= 21

...

... ...

am1

am2

...

amn

m,n

B = (b )

- матрица-столбец свободных членов,

m,1

...

bm m,1

X = (x

)

- матрица-столбец неизвестных.

n,1

...

xn ,1

Например, первое уравнение системы получено умножением первой

строки матрицы A на столбец неизвестных: a11x1 + a12 x2 +... + a1n xn = b1 .

Матрица, полученная из матрицы

A добавлением столбца свободных

членов, называется расширенной матрицей системы:

antigtu

a11

a12

...

a1n

...

A = (A

B)= с...

...

m,n+1

Упорядоче

ое

м ожество

из

величин

x1 = c1 ,

x2 = c2 , … xn = cn

называется реше ием СЛУ,

если при подстановке этих чисел в систему

уравнения превращаются в тождества. Решение может быть записано в

виде м трицы

X = (ck )n,1 = ...

n,1

Система ур внений называется совместной, если она имеет хотя бы од-

но решение, и несовместной, если у нее нет ни одного решения.

Система называется определенной, если она имеет единственное реше-

ние, и называется неопределенной, если она имеет бесконечное множе-

ство решений.

Скачано

Системы линейных уравнений

Система линейных уравнений (1)

называется неоднородной, если мат-

рица B не является нуль−матрицей ,

если

и называется однородной,

B = .

antigtu2

Однородная система всегда имеет

нулевое (так называемое тривиаль-

ное) решение: x1 = x2 =... = xn = 0 .

Например,

1).

Система x1 + x2 =1

несовместна, решений нет;

x1 + x2 = 2

2).

Система x1 + x2 =1

совместна, но не определена, так как имеет беско-

x1 + x2 =1

нечное множество решений: x =1−c, x = c

или (в матричной форме)

1 − c

X =

, где c - произвольная постоянная;

3).

Система x1 + x2 =1

, совместна и определена, так как имеет единствен-

x1 − x2 =1

ное решение: x1 =1,

x2 = 0

(или X = 1

3.2. Системы n линейных уравнений с n неизвестными.

Скачано

Матричный метод решения. Правило Крамера.

Метод Гаусса (мет д п следовательного исключения

переменных)

3.2.1. Системы n ли ей ых уравнений с n неизвестными

Система n линейных уравнений с n неизвестными имеет единственное

решение, если определитель основной матрицы A отличен от нуля.

Доказательство:

Запишем систему уравнений в матричном виде: A X = B , где

a11 ...

a1n

A = ... ...

... , X = (xi )n,1

= ... ,

B = (bk )n,1 = ... .

(2)

...

nn n,n

n,1

Пусть det A ≠ 0, тогда существует обратная матрица A−1 , A−1 A = E .

Умножим уравнение слева на A−1 :

A−1 A X = A−1B , X = A−1 B .

26							ru	Лекция 3
26								Лекция 3
		1. Если система n уравнений с n неизвестными имеет отличный от нуля
	С
		определитель, она может быть решена матричным методом.
		определитель, она может быть решена матричным методом.
		Например, система x1 + x2 =1 в матричном виде выглядит как
		x1 − x2 =1		antigtu		.
		x1 − x2 =1
		1	1	x	1
				1	= .
		1	−1	x2	1

, det A = −2

≠ 0 ,

−1

−

1 −1

−1

A =

−1

1 −1

−1 1

X = = −

= .

2 −1 1 1

2. Если однородная система

уравнений с

неизвестными имеет от-

личный от нуля определитель основной матрицы системы, то у нее су-

ществует только нулевое (тривиальное) решение.

Для однородной системы

B = ; A X = .

Так как существует A−1 ,

то

X =A−1 = .

3.2.2. Правило Крамера

Обозначим через ∆ - определитель

основной матрицы системы

(2)

(главный определитель системы)

∆ = det A =

a11

...

a1n

...

an1

...

ann

∆i - i-й вспомог тельный определитель системы (2), получается из ∆ заме-

ной i -го столбца на столбец свободных членов,

Скачано

a11

... a1,i−1

a1,i+1

...

a1n

∆

a21

...

a2,i−1

a2,i+1

...

a2n

... ... ... ... ... ... ...

an1

...

an,i−1

an,i+1

...

ann


	Системы линейных уравнений		27
		ru
.		ru

Т Если главный определитель системы линейных уравнений не равен нулю, то система совместна и определена, причём единственное решение

(x1, x2 ,…, xn ) вычисляется по формулам Крамера:

По теореме о разложении определителя по столбцу сумма в круглых скобках – это определитель матрицы Ai , которая отличается от матрицы

x =

∆1 , x =

∆2 , … , x =

∆n .

∆

Доказательство:

−1

(V )

Матрица, обратная к матрице

коэффициентов: A

( A )

, ее

det A

i+ j

−1

= (q j ) , q j =

(−1)i+ j

M ji

элементы A ij =

(−1)

Mij ,

det

det A

Запишем элемент произведения X = A−1 B :

(−1)i+k

i+k

xi = ∑qikbk = ∑

bk =

∑(−1)

bk Mki .

det A

k =1

det A k =1

antigtu

A тем, что i-й столбец заменен на столбец свободных членов.

Таким образом,				x = ∆i .					с
				i	∆
Пример:
Скачано							2x1		+3x2	+ 2x3 = 9,
	Решить систему:						x + 2x + 3x					=14,
								1	2	3
							3x + 4x			+ x		=16.
								1	2	3
	По формулам Крамера:
		2		3	2						9	3		2					2	9	2
		2		3	2						9	3		2					2	9	2
	∆ =	1		2	−3	= −6 ≠ 0, ∆1 =					14	2		−3	= −12,		∆2	=	1	14	−3	= −18,
		3		4	1						16	4		1					3	16	1
			2	3	9	=12.
			2	3	9
	∆3 =		1	2	14
			3	4	16
	Вычислим значения неизвестных:
							x =		∆1 = 2 , x =				∆2	= 3		, x =	∆3	= −2 .
								1	∆	2			∆			3	∆

28 Лекция 3

3.2.3. Метод Гаусса (метод последовательного исключения неизвестных)

Рассмотрим систему n уравнений с n неизвестными (2). Данная система с помощью элементарных преобразований приводится к эквивалентной сис-

теме, решение которой находится проще.
Элементарными преобразованиями системы являются следующиеru				:
	перемена местами двух любых уравнений системы;	.
	перемена местами двух любых уравнений системы;
	умножение любого уравнения системы на произвольное число k ≠ 0 ;
	antigtu
	прибавление к одному уравнению системы другого уравнения, умно-
	женного на произвольное число k ≠ 0 .
!	1). Элементарным преобразованиям уравнений соответствуют элемен-
	тарные преобразования строк расширенной матрицы системы		A		= (A	B).

2). Элементарные преобразования матрицы не изменяют ее ранга. 3). Метод Гаусса справедлив и для произвольных систем ( m ×n ).

Метод Гаусса предполагает следующий алгоритм:

= b

x +... + a

1. Для системы уравнений ..............................

Скачано

+... + a

= b

n1 1

записывают расширенную матрицу системы:

a11

a12

...

a1n

...

A = (A

B)=

... ...

... .

...

n,n+1

2. Элемент рными преобразованиями строк приводят ее к трапециевидной форме, при этом основн я матрица системы приводится к верхнему тре-

угольному виду.

3. Возвращаясь к системе уравнений, определяют все неизвестные.

Пример:

x1 + x2 + x3 = 6

Решить систему 2x1 − x2 + x3 = 3 .

x1 + x2 − x3 = 0

Для удобства будем обозначать строки матрицы αi , а столбцы – β j .

Системы линейных уравнений

1 1

α2 − 2α1

1 1 1

−1

−3 −1

−9

−

, вернемся к системе урав-

1 1 −1

0 0 −2

−6

antigtu

нений:

+ x

= 6

+ x

+ 3 = 6

− 3x2

− x3

= −9

− 3x2

− 3

.= −9

− 2 x3

= −6

= 3

+ 5 = 6

x2 = 2

x2 = 2 .

= 3

Употребляется также расширенный метод Гаусса,

или метод Гаусса –

Ньютона. В нем основная матрица системы элементарными преобразо-

ваниями строк преобразуется к диагональному виду, пункт 2 предыдущей схемы (так называемый прямой ход) дополняется обратным ходом

– преобразованием верхней треугольной матрицы к диагональной. Для предыдущего примера это будет выглядеть так:

1	1 1			6		1 1 1					6	1		1 0	3

0	−3 −1			−9		0 −3 −1					−9	0		−3 0	−6
	0	−2		−6										0 1	3
0						0 0 1					3	0
Скачано							с
			1		1 0			3	1 0 0			1
			0		1 0			2		0 1 0		2
													,
			0		0 1			3		0 0 1		3

откуда ответ очевиден.

3.3. Теорема Кронекера - Капелли

Р ссмотрим систему m -линейных уравнений с n -неизвестными (1).

В нач ле лекции было показано, что ее можно представить в матричном виде. Будем р ссм трив ть матрицу A размерности m ×n как набор строк αi (столб-

цовβj ):

Лекция 3

A = α2

или

A = (β , β

, ..., β

...

antigtu

αm

1 j

где α

= (a

,...,a ) – матрица - строка;

a2 j

- матрица-столбец.

Введем понятие линейной зависимости строк (столбцов) матрицы.

Линейной комбинацией строк называется выражение вида:

λα + λ α

+ ... + λ α

λα

2 2

k k

∑ i

i=1

= λ1 (a11 a12 ... a1n )+λ2 (a21 a22 ... a2

)+ ... + λk (ak1 ak 2 ... akn ).

Строки матрицы α1, α2 , ...,

αk

называют

линейно зависимыми, если

существует такой набор чисел λ1, λ2 , ..., λk , не равных одновременно ну-

лю, при которых линейная комбинация строк обращается в ноль:

Скачано

λ1α1 + λ2α2 + ... + λkαk = 0 .

Строки матрицы являются линейно зависимыми, если одна из них явля-

ется линейной к мбинацией

стальных:

= λα + λ α

+ ... + λ α

+ λ

+ ... + λ α

1 1

2 2

k −1 k −1

k +1 k

n n

Действиям

ад строками матрицы соответствуют действия над уравне-

ниями системы.

Пусть м трица A р змерности (m×n)

имеет ранг r . Отличный от нуля

минор порядка r , составленный из элементов матрицы A , называется

базисным минором матрицы A .

Неизвестные, коэффициенты перед которыми входят в базисный минор,

называются базисными неизвестными. Неизвестные, не являющиеся ба-

зисными, н зываются свободными.

Теорема о б зисном миноре. Если матрица (m×n) имеет ранг r , то су-

ществуют r

таких строк (столбцов), что все остальные строки (столбцы)

являются линейными комбинациями данных. Из элементов, входящих в

эти строки (столбцы), можно построить базисный минор матрицы.

! Базисных миноров может быть много, но ранг определяется одно-

Системы линейных уравнений

значно.

1). Строки (столбцы), входящие в базисный минор, линейно независимы.

2). Все строки (столбцы) матрицы, не входящие в базисный минор,

Так как добавление столбца B

в множе твоantigtu{β ,..., β } не увеличивает количество

линейно зависимы с базисными.

3). Число линейно независимых строк матрицы равно числу линейноru

не-

зависимых столбцов и равно рангу r .

4). rang (A)≤ min (m,n).

Теорема Кронекера - Капелли. Для того чтобы система m уравнений с

n неизвестными была совместной, необходимо

и достаточно, чтобы

ранг основной матрицы системы равнялся рангу расширенной матрицы:

Доказательство*:

r(Α) = r (Α

Β).

Достаточность. Пусть r(Α) = r(Α

Β). Рассмотрим столбцы матрицы A и

a21

, … , β

B =

линейно независимых столбцов,

толбец B есть линейная комбинация столбцов ос-

Скачано

новной матрицы, т.е. суще твуют такие x1, x2 ,…, xn ≠ 0 , что

B = x1β1 + x2β2 +…+ xn βn ,

или

= x

+ x

+...

+ x

= a

x +... + a

Записывая последнее в виде

= a

x +... + a

убеждаемся в том, то x1, x2 ,…, xn - решение системы, система совместна.

Необходимость. Пусть система совместна, x1, x2 ,…, xn - решение системы.

З писыв я систему в виде

11 x

+...

x1β1 + x2β2 +…+ xn βn = B ,

Лекция 3

видим, чтоB является линейной комбинацией β1,..., βn , добавление столбца свобод-

ных членов не увеличивает ранга матрицы, r( A) = r( A) .

Итак, если r(Α) ≠ r (Α

Β), то система заведомо не имеет решений; если же

r(Α) = r (Α

Β), то возможны два случая:

1) если r = n , тогда решение единственно;

2) если r < n , тогда решений бесконечно много.

3.4. Однородные системы линейных уравнений

Однородная система имеет вид:

+ a

x +... + a

= 0,

a21x1 + a22 x2 +... + a2

= 0,

............................................

+ a

x +

... + a

x = 0,

m1 1

m2 2

ей соответствует матричное уравнение Α Χ = .

Однородная система всегда совместна,

так как r( A) = r(

, поскольку

нулевой столбец не меняет ранг матрицыantigtu, всегда существует нулевое реше-

ние (0, 0, ..., 0) .

Для того чтобы дн р дная система имела ненулевое решение, необхо-

димо и достат чно, чт бы r( A) < n .

Доказательство:

r не может быть больше n (ранг матрицы не превышает числа столб-

цов или строк);

r ≠ n , т.к. если r = n , то главный определитель системы ∆ ≠ 0 , и, по

формул м Кр мера, существует единственное тривиальное решение

x1 = x2 =... = xn = 0 , что противоречит условию. Значит, r( A) < n .

Для того чтобы однородная система n линейных уравнений с n неиз-

вестными имела ненулевое решение, необходимо и достаточно, чтобы

∆ = 0 .

Скачано

Системы линейных уравнений

3.5. Схема отыскания общего решения системы m уравнений с n неизвестными

входят в общий базисный минор. Остальные уравнения являются линейными комбинациями этих уравнений и не несут дополнительной информации.

1. Находим ранги матриц A и (A

B).

Если r(Α) ≠ r (Α

Β ), то система не имеет решений.

Если r(Α) = r (Α

Β )= r , то у системы есть решения. У матриц A

есть общий базисный минор. Выбираем его.

2. Оставляем в системе только те уравнения, коэффициенты которых

antigtu

3. Сравниваем ранг и количество неизвестных.

Если r = n , то есть порядок базисного минора совпадает с количеством неизвестных, решаем систему n уравнений с n неизвестными (ее определитель ∆ ≠ 0) и получаем единственное решение.

Если r < n , то в системе имеются (

− r)

свободных неизвестных. Тогда

x1 , x2 , ..., xr

– базисные неизвестные, а

xr+1 ,

...,

xn – свободные неиз-

вестные.

Переносим свободные неизвестные в правую часть уравнений системы:

x + a

+... + a

= b

−... − a

x ,

− a

11 1

12 2

1r r

1,r+1 r+1

1n n

a21x1 + a22 x2 +... + a2r xr

= b2 − a2,r+1xr+1 −... − a2n xn ,

(3)

...........................................................................

Скачано

x + a

+... + a x

= b

− a

−... − a

x .

r1 1

2 2

rr r

r,r+1 r+1

rn n

или, в матричной форме,

AX r

= B0 + xr+1B1 + xr+2 B2 +... + xn Bn−r ,

(4)

где

a11

a12 ...

a1r

A =

a ...

, det A ≠ 0 ,

... ...

...

ar1

ar 2 ...

arr

a1,r+1

a1,n

, B

= 2

= − 2,r+1

, ...,

= − 2,n .

...

n−r

...

ar,r+1

ar,n

34	ru	Лекция 3

Система (3) является следствием исходной системы (1) и ее решение может

быть найдено любым ранее рассмотренным способом.									.
быть найдено любым ранее рассмотренным способом.
Пусть свободные неизвестные принимают значения
	xr+2 = c2			antigtu
xr+1 = c1 ,	xr+2 = c2			,	...,			xn = cn−r
Тогда система (4) принимает вид:
AX r = B0 + c1B1 + c2 B2 +... + cn−r Bn−r										(5)
и базисные неизвестные x1, x2 ,		..., xr		выражаются определенным образом
через эти значения: xi = xi (c1 ,	c2 , ...,				cn−r ) ,			i =1,2,..., r .	Решение неодно-
родной системы A X = B можно записать в виде матрицы-столбца:
x1(c1, c2 , ..., cn−r )
x (c , c , ..., c					−r	)
2	1		2		−r
...........................

X = xr (c1, c2 , ...,				c −r )			.			(6)
	с		c1
			c2
			c2
			...
			...
			cn−r
			cn−r
Скачано

Поскольку свободные неизвестные могут принимать произвольные числовые значения, то исходная система имеет бесконечно много решений. Выражение (6) называется бщим решением системы (1). Если константам c1, c2 , ..., cn−r придать к нкретные значения, то получим частное решение

системы (1).

Пример:

	2x		+3x	2	− x		3	= 2,
		1		2			3
Решить систему: 7x1 + 4x2 + 2x3 = 8,
			− 2x2 + 4x3							= 5.
	3x1		− 2x2 + 4x3							= 5.
Рассмотрим расширенную матрицу:
			2 3 −1						2					−1 3 2		2
			2 3 −1						2					−1 3 2		2
			7 4 2						8				~	2 4 7		8	~
(Α	Β )=		7 4 2						8	~	β3	↔ β1	~	2 4 7		8	~
			3 −2 4						5					4 −2 3		5
			3 −2 4						5					4 −2 3		5

			α2 + 2α1								−1	3	2	2
			α2 + 2α1								0	10	1112
			~ α			+ 4α				~	0	10	1112		.
					3			1			0	0	0	1
											0	0	0	1

Системы линейных уравнений																																ru	35
Системы линейных уравнений																																	35
		Следовательно, r(Α) = 2				и r(Α							Β) = 3 . Поскольку r(Α) ≠ r(Α																			Β) , система


																												.
																												.
		несовместна. Очевидно, что третье уравнение преобразованной системы:
		0 x1 +0 x2 +0 x3 =1 не имеет решений.
	Пример:														antigtu
															antigtu

					x1 − x2 + x3									=12,
				2x1 +3x2 − x3										=13,
				2x1 +3x2 − x3										=13,
		Решить систему			3x2 + 4x3									= 5,
					3x2 + 4x3									= 5,
			−3x + x				2		+ 4x				3	= −20.
					1		2						3
		Рассмотрим расширенную матрицу:
				1 −1 1							12															1 −1 1				12
				1 −1 1							12															1 −1 1				12
				2 3 −1							13						α				−2α					0 5 3			−11
		(Α	Β) =													~			2			1		~								~
				0 3 4							5						α				+3α					0 3 4			5
				0 3 4							5						α				+3α					0 3 4			5
																			4			1
																										0	−2 7		16
			−3 1 4								−20															0	−2 7		16
			−3 1 4								−20
					1	−1				1		12													1		−1	1			12
					1	−1				1		12
					0 3 4							5						α2 −α3
					0 3 4							5						α2 −α3
		~ α2 +α4 ~				с						5				~ α					↔	α			~ 0 −2 7						16 ~
		~ α2 +α4 ~			0 3 4							5				~ α					↔	α			~ 0 −2 7						16 ~
																				4			2		0		3	4			5
					0	−2				7		16
	Скачано
								1 −1 1													12				1 −1 1			12

			~ 2α3 +		3α2	~				0 −2 7											16	~			0 −2 7			16
			~ 2α3 +		3α2	~				0 −2 7											16	~			0 −2 7			16
										0 0 29											58				0 0 1			2
										0 0 29											58				0 0 1			2

		Следовательно, r(Α) = r(Α							Β) = 3 ,							поэтому система совместна и имеет
		Следовательно, r(Α) = r(Α							Β) = 3 ,							поэтому система совместна и имеет
		еди стве ое реше ие.
																		x − x						+ x =12,
																					1	2				3
		Преобр зов нн я система имеет вид:																			− 2x2 + 7x3 =16,
																									x3		= 2,
																									x3		= 2,
		ее решение: x1 =9,		x2 = −1, x3 = 2 .

Лекция 3

Пример:

−4x

+ 2x

= −1,

Решить систему

2x1 −3x2 − x3 −5x4

= −7,

= −8.

3x1 −7x2 + x3 −5x4

Рассмотрим расширенную матрицу:

1 −4 2 0

−1

α2 −2α1

−4 2 0

(Α

Β) =

−3 −1 −5

−7

0 5 −5 −5

−5

~ α

−

3α

−7 1 −5

−8

0 5 −5 −5

−5

1 −4 2 0

−1

1 0 −2 −4

−5

~ α

−

0 1 −1 −1

−1

~ α

+ 4α

0 1 −1 −1

−1

0 0 0 0

Следовательно, r(Α) = r(Α

Β) = 2 , поэтому система совместна и не опре-

делена. Выберем

и x2 в качестве базисных неизвестных и запишем

преобразованную систему:

= −5 + 2x

+ 4x

x2 = −1 + x3 + x4 .

Полагая x3 = c1 ,

x4 = c2 ,

где c1

− произвольные числа, получаем об-

щее решение

и темы

antigtu

−5 + 2c +

−5

−1

X =

−1+ c1 + c2

+ c1

+ c2

Реше ие соответствующей однородной системы

x − 4x

+ 2x

= 0,

2x1 − 3x2 − x3 − 5x4 = 0,

− 7x2 + x3 − 5x4

= 0

3x1

можно записать в виде:

Скачано

X = c

+ c

Системы линейных уравнений

3.6*. Фундаментальная система решений

Если СЛУ имеет вид A X = c1B1 + c2 B2 ,

то ее решение может быть записано в виде

X = c1 X1 +c2 X2 , где

и X 2

- решения систем

A X = B1 и A X = B2

соответствен-

но.

Доказательство:

= A−1 B

X = A−1 (c B + c B

)

= A−1 (c B )

+ A−1 (c B

= c A−1 B +c A−1 B = c X

+c X

В предыдущем параграфе возникла система (5)

AXr

= B0 +c1B1 +c2 B2 +... +cn−r Bn−r .

Из только что доказанной теоремы следует, что

= Xr ,0 +c1 Xr ,1 +c2 Xr,2 +... + cn−r Xr ,n−r ,

(7)

где Xr,0 , Xr,1,

Xr,2 , ..., Xr,n−r

- решения системы (5) при подстановке в нее (5) вместо

правой части столбцов B0 ,

B1, B2 , ..., Bn−r .

antigtu

Поскольку X

что базисные неизвестные линейно зависят от

, это означает,

...

свободных неизвестных и в выражении

x1 (c1, c2 , ..., cn−r )

x (c , c , ...,

)

n−r

...........................

xr (c1, c2 , ..., cn−r )

(8)

X =

...

cn−r

для общего

решения

системы

xi = xi (c1, c2 , ..., cn−r )

линейные функции

c1, c2 , ..., cn−r .

Это позволяет записать матрицу–столбец (6) - общее решение системы (1) в виде:

X = X0 +c1 X1 +c2 X2 +...+cn−r Xn−r ,

(9)

Скачано

38														ru		Лекция 3
38																Лекция 3
	где частные решения Xi					(i = 0, 1, 2, ..., n −r) , образующие фундаментальную сис-
	тему решений, получены при следующих значениях постоянных в выражении (5):
	x1 (0, 0, ..., 0)				x1 (1, 0, ..., 0)				x1 (0, 1, ..., 0)				x1 (0, 0, ..., 1)
		СЛУ);			x (1, 0, ..., 0)				antigtu				x (0, 0, ..., 1)
	x (0, 0, ..., 0)				x (1, 0, ..., 0)				x (0, 1, ..., 0)				x (0, 0, ..., 1)
	2				2					2			2
	....................				....................				....................							.........

X = xr (0, 0, ..., 0)			,	X = xr (1, 0, ..., 0)			, X		= xr (0, 1, ..., 0)		, ..., X		= xr		(0, 0, ..., 1)		.
0				1				2				.
		0				1				0						0
		0				0				1						0
		...				...				...						...
		...				...				...						...
		0				0				0						1
		0				0				0						1
	Выражение (8) называется разложением по фундаментальной системе решений.

	В результате изучения материала, изложенного в этой лекции,
	студент должен знать:
	основные понятия теории СЛУ (основная и расширенная мат-
		рицы		системы,		совместные			/	несовместные, определен-
						с
		ные/неопределенные однородные/неоднородные системы, ба-
		зисные и свободные неизвестные, общее и частное решение
		способ выяснения, имеет ли					и тема решения
		(теорема Кронекера – Капелли);
	Скачано
		методы решения СЛУ – матричный, правило Крамера, метод
		Гаусса;
		схему отыскания				бщего решения СЛУ.

Студент должен п нимать, что преобразования строк матриц системы соответствуют пре браз ваниям уравнений системы.

Лекция 4 ВЕКТОРНАЯ АЛГЕБРА

В лекции 4 излагаются элементы векторной алгебры. Необходимость применения

ством и наглядностью математических формулировок законов, сколько объективными свойствами изучаемых явлений. Направленные величины используются при описании широкого круга явлений, относящихся к теоретической механике, механике жидкости и газа, теории электромагнетизма. Курс математики для инженерных специальностей включает также элементы векторного анализа, который будет излагаться после изучения дифференциального и интегрального исчислений одного и нескольких переменных.

векторного исчисления при изложении технических дисциплин вызвана не столько удоб-
antigtu	.	ru

4.1.	Основные определения
4.2. Линейные операции над векторами
4.3.* Линейная зависимость векторов.
	Геометрические критерии линейной зависимости.
4.4.	Базис и координаты
4.5. Ортонормированный базис. Декартова прямоугольная система
	координат
4.6.	Скалярное произведение векторов. Определение.
		с
	Алгебраические свойства. Геометрические приложения.
	Выражение через декартовы координаты сомножителей
4.7.	Векторное произведение векторов. Определение.
	Алгебраические и геометриче кие свойства. Выражение через де-
	картовы координаты омножителей
Скачано
4.8.	Смешанное произведение векторов. Определение.

Алгебраические и геометрические свойства. Выражение через декартовы к рдинаты с мн жителей

4.1. Основные определе ия

Величины, для определения которых достаточно знать одно число, называются ск ляр ми (температура, масса, работа силы, плотность). Величины другого рода х р ктеризуются не только численным значением, но и направлением в пространстве. Таковы перемещение, скорость, ускорение, сила, напряженность электри еского поля и т.д. Рассмотрение такого рода величин приводит к понятию вектора.

О Геометрическим вектором (вектором) назы-

вается направленный отрезок (отрезок, у которого одна граничная точка считается начальной, другая – конечной).

падают: 0G, 0G = 0 .

Лекция 4

На чертеже вектор обозначается стрелкой; над буквенным обозначением

JJG

вектора также ставится стрелка AB , a .

Длиной вектора (модулем) называется расстояние между началом и кон-

JJG

цом вектора. Обозначение:

или

Нулевым вектором называется вектор, у которого начало и конец сов-

Векторы называются коллинеарными, если лежат на одной прямой, ли-

бо на параллельных прямых.

Нулевой вектор коллинеарен любому вектору.

Три вектора называются компланарными, если они лежат в одной

плоскости или в параллельных плоскостях.

Если тройка векторов содержит нулевой вектор или пару коллинеарных

векторов, то эти векторы компланарны.

Вектор, фигурирующий в определении, носит название связанного, или

закрепленного вектора.

JJJG

Если же точка приложения вектора (точка

A для вектора

AB ) может

быть выбрана произвольно, вектор называется свободным. Если точка

приложения может двигаться по линии действия вектора, говорят о

скользящем векторе. Иначе говоря, свободный вектор aG

является пред-

ставителем бесконечного множе тваantigtuсвязанных или скользящих векто-

ров.

Скачано

матривать только

В дальнейшем мы будем ра

свободные векторы. Для них, в частности, спра-

ведливо следующее пределениес .

Два вектора равны, если

ни коллинеарны, име-

ют одинаковую длину и направление.

Например, aG = bG.

4.2. Линейные опер ции над векторами

Суммой aG +b двух векторов

и b

называется

векторG, идущий из начала вектора a в конец век-

тора b при условии, что начало вектора b

при-

ложено к концу вектора a (правило треуголь-

ник ).

Векторная алгебра

Свойства операции сложения векторов:

1˚.

= b

+ a

(переместительное свойство).

2˚.

(сочетательное свойст-

+b )+ c

= a +(b

+ c )

во).

antigtu

3˚. Существует нулевой

вектор

0 ,

такой,

что

+ 0G

= aG

для любого вектора

(особая роль

нулевого вектора).

aG существует противо-

4˚.

Для каждого вектора

положный

ему

′

такой,

что

вектор a =

−a ,

+ (−a ) =

0 .

Свойства доказываются геометрически. Докажем, например, свойство 1˚.

Рассмотрим

произвольный

параллелограмм

ABCD

Пусть

JJG

a = AB ,

JJJG

JJG

JJJG

JJG

JJJG

= BC . Тогда a

+b = AC

. Но BC

AD ,

DC =

AD + DC

= b

+ a .

Таким образом, a +b

= b + a .

При

доказательстве

свойства

1˚ обосновано

еще одно правило сложения векторов, назы-

ваемое правилом параллелограмма: если

векторы a и b приложены к общему началу и

на них построен параллелограмм, то сумма

Скачано

этих векторов представляет собой диа-

гональ параллел грамма, идущуюс

из общего

начала векторов

a и b .

Вычитание вект р в

пределяется через сложение:

−b = a + (−b) .

Иначе: если векторы

и b

приложены к общему началу, то разностью

−b ,

векторов a

и b будет вектор a

идущий из конца вектора b

к концу

вектора aG.

Произведением αaG

вектора a на вещественное число α

называется

вектор bG, коллинеарный вектору a , имеющий длину

и на-

правление, совпадающее с направлением вектора a

в случае α > 0 и

противоположное направлению вектора a в случае α < 0 .

Геометрический смысл операции умножения вектора на число:

при умножении вектора aG на число α вектор a «растягивается» в

раз

при

>1, при 0 <

<1 вектор «сжимается» в

раз. Если α < 0 , век-

тор, кроме этого, меняет направление на противоположное.

чиселG).

Лекция 4

Свойства операции умножения вектора на число:

5˚.

α(a +b )=αa +αb

(распределительное свойство

суммы

относительно

6˚.

векторов).

antigtu

(α + β )aG =αaG + βaG (распределительное свойство относительно суммы

7˚.

α(βa)= (αβ )a (сочетательное свойство чи-

словых сомножителей).

8˚.

1 aG = aG

(существование единицы).

ДокажемG

например, свойство 5˚. Отложим

векторы a и

от общего начала и построим на

них параллелограмм, диагональ которого будет

представлять собой сумму aG

+b . При «растяжении» (α >1 ) сторон этого па-

раллелограмма в α

раз его диагональ также «растягивается» в α раз, но это и

означает, что сумма αa

+αb

равна α(a + b) .

Свойства 1˚ ÷ 7˚ для векторов позволяют производить выкладки в век-

торной алгебре по тем же правилам, по которым производятся аналогич-

ные выкладки в алгебре вещественных чисел.

4.3.* Линейная зависимо ть векторов.

Скачано

Геометрические критерии линейной зависимости

Линейной комбинацией вект рсв a , aG , ..., aG называют выражение:

+ ...

α1a1 + α2a2

+αnan =

∑αi ai ,

i =1

где α , α

, ..., α

- произволь ые действительные числа.

Система векторов a1

, a2 , ..., an

называется линейно зависимой, если существуют

действительные числа α1 , α2 , ..., αn , такие, что хотя бы одно из них отлично от нуля,

и выполняется р венство:

α aG

+ α aG

+ ...+α aG = 0 .

(*)

1 1

2 2

n n

В противном слу ае,

т.е. если линейная комбинация (*) обращается в ноль только

при всех αi

= 0,

i =1, ..., n , то система векторов называется линейно незави-

симой.

Если векторы линейно зависимы, то любой вектор может быть выражен в виде ли-

нейной

омбинации остальных. Например, если αn ≠ 0 , то из (*) следует, что

n−1

, где β1

= −

α1

, ..., βn−1

= −

αn−1

an = β1a1

+ β2 a2 + ...+βn−1an−1 =

∑βi ai

αn

i=1

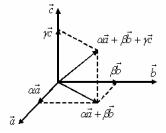
Векторная алгебра

Геометрические критерии линейной зависимости

Система двух ненулевых векторов a1 ,

aG2

линейно зависима тогда,

и только тогда,

когда векторы коллинеарны.

antigtu

Доказательство:

α2 aG

4.4. Базис и координаты

= −

; или

Необходимость. Пусть

α aG + α

= 0 и α ≠ 0 . Тогда α aG

= −α aG

1 1

2 2

1 1

2 2

= λaG , где λ = −α2 .

α1

Достаточность.

Пусть

= λa .

Запишем это

равенство

в виде

−λa

= 0

или

α a

+ α

= 0 ,

где α =1, α

= −λ ≠ 0 . Итак, существует нулевая линейная комби-

нация с ненулевыми коэффициентами, а это и означает, что система векторов линей-

но зависима.

Система трех векторов aG1, aG2 , aG3 линейно зависима тогда и только тогда, когда век-

торы компланарны.

т.е. для любых aG1, aG2 , aG3 , aG4

Система четырех векторов всегда линейно зависима,

найдутся

такие

числа

α ,

, α

не

равные

одновременно нулю,

что

+ α

+α

G 1

α a

= 0 .

Базисом в пространстве будем называть три некомпланарных вектора,

Скачано

взятые в определенном порядке.

Базисом на плоск сти будем называть два неколлинеарных вектора на

этой плоскости, взятые в

пределенном порядке.

Базисом на прям й будем называть любой ненулевой вектор этой пря-

мой.

Каждый вектор может быть разложен по базису в пространстве и это

разложение единственно.

Иначе, если aG

, bG, cG

– три некомпланар-

ных вектора в простр нстве, то любой вектор

может

быть

записан

виде:

=αa + βb +γc .

Док з тельство возможности:

} - некоторый базис в простран-

Пусть {a, b,

стве, dG - произвольный вектор.

Тогда

αaG + βb +γcG = 0G

только

при

α = β = γ = 0 .

α aG +α

bG +α

cG +α

= 0 , при этом α4 ≠ 0 ,

так как если

Лекция 4

α4 = 0 , то α1aG +α2bG +α3cG = 0 , а этого быть не может, т.к. {aG, bG, cG} - ба-

зис.

Тогда G

α1

α2

α3

d = −α a −α

b −α

c , d = −

antigtu

=αa + βb +γc .

α4

Доказательство единственности:

по базису

Предположим, что существуют два разложения вектора

G G

то есть

;

d =

{a, b,

α1a

β1b

+γ1c

α2a + β2b +

γ2c . Вычтем из од-

ного равенства

другое:

(

Так как

(α1 −α2 )a

β1 − β2 )b + (γ1 −γ2 )c

G G

}- базис, ни один из векторов

} не может быть выражен

{a, b, c

{a, b,

через

другие

при

ненулевых

коэффициентах,

поэтому

α1 =α2 ,

β1 = β2 ,γ1 =γ2 .

Геометрически вектор

представляет собой пространственную диаго-

наль параллелепипеда, построенного на векторах a ,

b и сG.

Коэффициенты разложения вектора по базису называются координата-

ми вектора в данном базисе и в каждом базисе определяются одно-

значно:

{

d =αa + βb +γc =

, β,γ

При сложении двух векторов d

и d

их координаты (относительно лю-

Скачано

бого базиса) складываются. При умножении вектора dG1 на любое число

α все его координаты умн жаютсяс

на это число.

Доказательств :

Пусть

=α

. Тогда в силу свойств 1˚-7˚

=α a +

β b +γ c

a + β

линейных операций

ад векторами

)bG

)cG,

dG + dG

= (α +α

)aG

+ (β

+ β

+ (γ

+γ

λdG

)aG

= (λα

+ (λβ )bG

+ (λγ

)cG.

В силу единственности разложения вектора по базису теорема доказана.

Системой координат в

пространстве

называют

совокупность базиса

G G

}

и некоторой точки, называемой началом координат.

{a, b,

JJJJG

Вектор OM , идущий из начала координат в точку M , называется ради-

ус-вектором точки M .

JJJG

Координ т ми точки M (α, β,γ )

называются координаты вектора OM .

Та им образом,

координаты радиус-вектора

JJJG

и координаты точки

M совпадают.

Векторная алгебра

4.5. Ортонормированный базис. Декартова прямоугольная система координат

Пусть в качестве базиса выбраны три взаимно перпендикулярных векто-

ра с длинами, равными единице.

G G

Обозначения: {i, j,k},

Такой базис называется

ортонормированным

(ОНБ). Векторы iG,

Gj, kG

называются базисны-

ми ортами. Зафиксируем точку О – начало ко-

ординат и отложим от нее векторы i ,

j, k . По-

x i 0

лученная система координат называется пря- X

моугольной декартовой. Координаты любого

вектора в этом базисе называются декартовыми

координатами вектора:

aG ={x, y, z} = x iG+ y Gj + z k

Прямые линии, проведенные через начало координат по направлениям

базисных векторов, называются координатными осями: Gi – порождает

– порождает antigtuOz . Координаты точки М (вектора

Ox ; j – порождает

Oy ; k

JJJJG

Oy , Oz называются

OM ) в декартовой си теме координат по осям Ox ,

соответственно абсциссой, ординатой и аппликатой.

Декартовы прямоугольные координаты

x, y, z вектора a равны проекци-

ям этого вектора на

си Ox ,

Oy , Oz соответственно; другими словами,

x = npOX aG =

cosα ,

y = npOY a =

cos β , z = npOZ aG =

cosγ .

Здесь α, β, γ

– углы, которые составляет вектор

a с координатными

осями Ox , Oy , Oz соответственно, при этом cosα ,

cos β , cosγ

называ-

ются напр вляющими косинусами вектора a .

Вектор aG0 =

={cosα, cos β, cosγ} представляет собой вектор единич-

Скачано

ной длины данного направления, или орт данного направления. Для напр вляющих косинусов справедливо соотношение:

cos2 α + cos2 β + cos2 γ =1.

Лекция 4

4.6. Скалярное произведение векторов. Определение.

Алгебраические свойства. Геометрические приложения.

Выражение через декартовы координаты сомножителей

antigtu

G G

Углом между векторами a и b

(обозначается (a , b )) называется наи-

меньший угол, на который надо повернуть векторa

до.совмещения с

вектором bG.

Проекцией вектора aG

на ось l,

прl a , называ-

ется величина А`В` направленного отрезка

JJJJJG

оси l.

A`B`

(

)

прl a =

cosϕ =

cos a , l0

где

- орт

оси l.

Скалярным произведением двух векторов называется число, равное

произведению длин этих векторов на косинус угла между ними:

G G

(a b )= (a,b )= b =

cos(a , b ).

Если один из векторов aG,

нулевой, то

(

G b

)

= 0 .

Алгебраические свойства

калярного произведения:

Скачано

1˚.

(a b )=(b

a).

Переместительное свойство:

2˚.

Сочетательное св йство:

(λaG b )= λ(aG bG)= (aG λbG)

3˚.

Распределитель

ое свойство:

((aG +b ) cG)= (aG cG)+(bG cG),

(aG (b + cG))= (aG bG)+(aG cG).

4˚.

G G

, если

= 0 .

(a, a)> 0

≠ 0 , и (a,

a)= 0 , если a

Доказ тельства свойств следуют из определения.

Геометри еские приложения скалярного произведения:

1. Связь с понятием модуля:

G G

cos0

;

G G

(a,a)=| a | | a | cos

a , a

(a, a ) .

(aG, b )

Косинус угла между векторами:

cos(a , b )=

вязь с понятием проекции.

Векторная алгебра

Проекция прGaG

вектора aG на вектор b :

(a, b )

G (a, b )

прbGa =

cos(a , b )=

, т.е. прbGa =

antigtu

(a, b )

Аналогично: прaGb

Необходимым и достаточным условием ортогональности (перпендику-

лярности) двух ненулевых векторов является равенство нулю их скаляр-

G G

ного произведения: a b : (a , b )= 2 (a,b) = 0 .

Выражение скалярного произведения векторов

через декартовы координаты сомножителей

Если два вектора

заданы своими декартовыми прямоугольными

координатами

a ={x1,

y1,

z1},

b ={x2 ,

y2 , z2},

то скалярное произведе-

ние этих векторов равно сумме парных произведений их соответствую-

щих координат, т.е. (a, b )= x1x2 + y1 y2 + z1z2 .

Доказательство: a

= x i

+ y j

+ z k

b = x i + y

+ z

k .

В силу свойств 2 и 3 имеем:

(aG, bG)=

((x1iG + y1 Gj + z1kG),(x2iG + y2 Gj + z2kG))=

Скачано

G G

= x1x2 (i ,i )+ x1 y2

(i , j )+ x1z2 (i ,k )+

+y1x2 (Gj,iG)+ y1 y2 (Gj, Gj )+ y1z2 (Gj,k )+

+z1x2 (kG,iG)+ z1 y2 (kG, Gj )+ z1z2 (kG,kG).

Так как i j , i k

, j

Gj) =1 1 cos90o = 0 .

то (iG, Gj) = (iG, kG) = ( Gj,iG) = ( Gj, kG) = (kG,iG) = (kG,

G G

=1.

Но (i ,i )

=| i

| cos(i ,i ) =| i

=1, аналогично ( j, j) =1

, (k , k )

Таким образом, (a, b )= x1x2 + y1 y2 + z1z2 .

1. Длина ве тора: aG ={x,

y, z},

(aG, aG) =

x2 + y2 + z2 .

2. Расстояние между двумя точками:

Если A=(x1, y1,

z1 ), B =(x2 ,

y2,

z2 )

– точки,

48 Лекция 4

то ρ(AB) =

JJJG

= (x −x )2

+(y − y )2

+(z −z )2 .

3. Угол между векторами:

Если aG = (x1, y1, z1 ),

= (x2 , y2 ,

z2 ), то

(aG,

b )

x x

y y

z z

cos(a

, b )=

+ 2

4. Проекция прGaGвектора a на вектор b

(aG, b )

x1x2 + y1 y2

+ z1z2

прbGa

x22 + y22

+ z22

5. Направляющие косинусы вектора:

cosα

= cos a,

x2 + y2 + z2

cos β

= cos

x2 + y2 + z2

cosγ

= cos a,

;

antigtux + y + z

cos2 α + cos2

β + cos2

γ = 1

4.7. Векторное пр изведение векторов. Определение. Алгебраические свойства. Геометрические приложения. Выраже ие через декартовы координаты сомножителей

	Упорядоченн я тройка некомпланарных векторов	a	,	aG	, aG	, приведен-
О
		1		2	3

ныхGк одному н ч лу, называется правой, если из конца третьегоG вектора a3 кр тч йший поворот первого вектора a1 ко второму a2 виден со-

вершаемым против часовой стрелки. В противном случае тройка назы-

вается левой.		JG
JJG		JG
a3	JJG	a3	JJG
	a2		JJG
			a2
	JG	G
	a1	a1
	правая	левая
Скачано

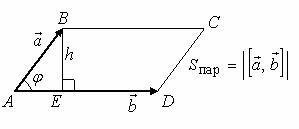
Векторная алгебра

Система координат называется правой, если ее базисные векторы обра-

зуют правую тройку.

В дальнейшем мы будем рассматривать только правые системы коорди-

нат.

При перестановке местами двух соседних векторов ориентация тройки

меняется.

Если тройки

b c a ,

c a b

правые,

то

G G

a b c ,

a c b ,

c b a ,

b aG c - левые. При круговой (циклической) перестановке.векторов ори-

ентация тройки не меняется.

Векторным произведением вектора a на вектор b

называется вектор

c =

a, b

= a ×b

= a

×b , удовлетворяющий следующим трем требова-

ниям:

на синус

1). Длина вектора c равна произведению длин векторов

и b

JGG

угла между ними, т.е.

sin (a,b).

a, b

2). Вектор c ортогонален к каждому из векторов a и b , т.е. c перпенди-

кулярен плоскости, в которой лежат векторы

и b .

b c является правой.

3). Вектор c направлен так, что тройка

Алгебраические свойства векторного произведения:

antigtuG

1˚.

Антиперестановочность

омножителей:

a, b

= − b, a .

2˚.

Сочетательное свойство:

αa,

G G

3˚.

Распределительн е св йство:

+ b, c

=[a, c]

+ b, c

4˚.

для люб го вект ра a .

[a, a]

= 0

Геометрические свойства векторного произведения векторов:

равен площади

Модуль вектора

Sпар параллелограмма, построен-

ного на вектор х a и b .

Площадь параллелограмма, построенного на векторах a и bG, равна

JJJG

пар

=| AD |

| BE |=| b |

h =| b || a | sin(a , b) .

Скачано

Лекция 4

Необходимым и достаточным условием коллинеарности двух векторов

является равенство нулю их векторного произведения.

Доказательство:

Необходимость. Пусть aG

и b коллинеарны.

G G

Тогда

[a , b]

[a , b] = 0 .

=| a | | b | sin (a , b )= 0

Достаточность.

G G

Пусть [a,b] = 0

[a , b]

= 0

| a | | b | sin (a , b )= 0 .

Тогда существуют три возможности: 1) либо sin (a , b )= 0 ,

2) либо aG = 0 ,

G G

3) либо b = 0 .

a коллинеарен b ; 2) и 3) a коллинеарен b

1) sin (a , b )= 0

, b )= 0,

по определению.

Выражение векторного произведения через координаты сомножите-

лей. Если два вектора aG

и b заданы своими декартовыми координатами

aG =

{

x , y , z

, b =

{

x , y

, z

antigtu

то их векторное произведение имеет вид:

c =

={y1z2 − z1 y2 , z1x2 − x1z2 , x1 y2 − y1x2},

или в виде симв лическ г

спределителя (более удобном для запомина-

ния):

c = a,

Доказ тельство:

Тройка {iG,

Gj, k} - пр вая. Преобразуем:

c = a ×b

= (x1i

+ y1 j

+ z1k )×

(x2i

+ y2 j

+ z2k )

G G

= x1 x2 i

× i

+ x1 y2 i

+ x1 z2 i × k

G G

+ y1x2 j

×i

+ y1 y2 j × j

+ y1z2 j

×k

+z x

×iG

+ z y

× Gj

+ z z

kG×kG .

Скачано

Векторная алгебра

Заметим, что

G G

×i

= j × j

= k ×k

=0, i

× j

− j ×i

= k,

iG×kG = − kG×iG = −Gj,

Gj ×kG

= − kG

× Gj = iG

antigtu

С учетом этих равенств выражение для c

можно представить в видеru

= ( y1z2 − z1 y2 ) i −(

x1z2 − z1x2 )

a, b

j +

(x1 y2 − y1x2 )

k ,

что можно выразить через определители:

aG,

b =

−

Если два вектора aG = (x1,

y1, z1 ) и b = (x2 ,

y2 , z2 )

коллинеарны, то их ко-

ординаты пропорциональны, то есть

4.8. Смешанное произведение векторов. Определение.

Алгебраические и геометриче кие свойства.

Скачано

Выражение через декартовы координаты сомножителей

Если вектор aG

умн жить вектсрно на вектор b ,

а результат

aG, bG

ска-

лярно умножить на вект р c , то полученное число называется смешан-

ным произведе ием векторов a ,

b ,

c : ( aG, b ,

cG)= aGbGcG.

Смешанное произведе ие

екомпланарных векторов a , b ,

c по абсо-

лютной величине р вно объему параллелепипеда, построенного на этих

векторах, приведенных к одному началу. Оно положительно, если тройка

G G

b , c

, b , c пр в я и отриц тельно, если она левая. Если же векторы a

G G

компланарны, то a b c равно нулю.

Доказательство:

Объем п раллелепипеда равен произведе-

нию площ ди основания на высоту.

bG, cG

осн.

;

h =

cosθ

;

bG, cG

cosθ

V = Sосн. h =

= (aG , b , cG )=

aGb cG

Лекция 4

Знак смешанного произведения зависит от знака

cosθ :

G GG

> 0 , если

a b c

вектор

направлен в ту же сторону, от плоскости, определяемой векто-

что и вектор

, т.е. когда тройка векторов правая; ана-

рами b и c ,

antigtu

логично доказывается, что aGb cG < 0 для левой тройки

плоскости,

Если же векторы aG, b и c компланарны, то вектор c лежит вru

определенной векторами

a и b , следовательно, прeG c

= 0

([a,b

],c )= 0 .

G G

G G G

G G

([a,b

],c )= ([b

,c],a)= ([c,a

],b ), поскольку тройки

a b c и b c a , c a b

имеют одинаковую ориентацию (циклическая перестановка векторов в

смешанном произведении не меняет его знака).

Нециклическая перестановка векторов в смешанном произведении

приводит к изменению ориентации тройки векторов и смене знака сме-

шанного

произведения:

GG G

G G G

G GG

Это

означает, что

b a c

= a c b

= c b a

= −ab c .

G G

смешанное произведение можно записывать просто в виде a b c , так как

G G

]) (смешанное произведение

зависит от

([a,b],

c )

= ([b

= (a , [b,c

порядка сомножителей, но не зависит от того, какие сомножители связа-

ны первичным знаком векторного произведения).

2. Критерий компланарно ти трех векторов. Необходимым и достаточ-

ным условием компланарно ти трех векторов является равенство нулю

их смешанного произведения.

Доказательство:

0 , то должно выполняться хотя бы одно из

Если a b c =

cosθ =

условий:

= 0 => векторы компланарны;

G G

b,c

= 0 , если b и c коллинеарны, => a , b , c - компланарны;

cosθ = 0 , тогда aG b, cG

, т.е. a компланарен

b и c .

G G

Скачано

Обратно, если a

, b , c - компланарны и не имеют место случаи 1) и 2),

то имеет место случай 3).

Векторная алгебра

Выражение смешанного произведения через

декартовы координаты сомножителей

Если три вектора

заданы своими декартовыми координатами

, b

a = x1i + y1 j + z1kG,

Gb = x2i + y2 j + z2k ,

antigtu

то смешанное

c = x3i

+ y3 j + z3k ,

произведение

a b c

равняется определителю,

строки которого соответ-

ственно равны координатам перемножаемых векторов:

a b c =

Доказательство:

cG =

b ,

= i

− j

+ k

(a,

b ,

c )= x1

− y1

+ z1

Необходимым и достаточным у ловием компланарности трех векторов,

заданных в декартовом бази е, является равенство нулю определителя

Скачано

третьего порядка, в первой строке которого записаны координаты перво-

го вектора, во второй - второгос, в третьей - третьего.

В результате изуче ия материала, изложенного в этой лекции,

студент должен з

ать:

р зличия между ск лярными и векторными величинами;

определения и свойства линейных операций над векторами

(сложение и умножение на число);

понятие базиса и координат вектора в данном базисе;

определения скалярного, векторного и смешанного произведений;

алгебраи еские и геометрические свойства произведений векторов;

выр жение произведений векторов через координаты сомножителей;

что вычисляется с помощью произведений векторов:

лярного (число) – длины векторов, углы, проекции,

ве торного (вектор) – площади треугольников и параллелограммов,

смешанного (число) – объемы.

Лекция 5 . ru

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ

Предметом изучения аналитической геометрии является описание геометрических объектов на плоскости и в пространстве с помощью уравнений. Методы аналитической геометрии широко используются в современном естествознании и прикладных техниче-

ских дисциплинах при построении математических моделей объектов и процессов. В лекции 5 рассматриваются наиболее простые объекты, описываемые уравнениями первой степени – плоскости и прямые. Приводятся различные виды уравнений плоскостей и прямых в пространстве, показывается, для какого типа задач тот или иной тип более уместен. Примеры иллюстрируют методы решения типичных задач.

5.1.	Основы аналитической геометрии
	5.1.1. Уравнение поверхности
	5.1.2. Уравнения линии
5.2.	Плоскость в пространстве
	5.2.1. Плоскость как поверхность первого порядка.
	Общее уравнение плоскости.
	5.2.2. Неполные уравнения плоскостей
	5.2.3. Уравнения плоскости «в отрезках»
	5.2.4. Нормальное уравнение плоскости
			antigtu
	5.2.5. Расстояние от точки до плоскости
	5.2.6. Уравнение пло ко ти, проходящей через три данные точки
	5.2.7. Угол между двумя плоскостями
	5.2.8. Условие параллельности и перпендикулярности плоскостей
5.3.		с
	Прямая линия в пр странстве
	5.3.1. Вект рн е уравнение прямой
	5.3.2. Параметрические уравнения прямой
	5.3.3. Ка о ические уравнения прямой
	5.3.4. Урав е ия прямой, проходящей через две данные точки
	5.3.5. Общие урав ения прямой
	5.3.6. Ур внение пучка плоскостей, проходящих через прямую
	5.3.7. Угол между двумя прямыми. Условия параллельности
	и перпендикулярности двух прямых
5.4.	Прямая и плоскость
	5.4.1. То ка пересечения прямой и плоскости
	5.4.2. Угол между прямой и плоскостью. Условия параллельности
	и перпендикулярности прямой и плоскости
Скачано

1 / 151 2 3 4 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в папке Лекции

#
13.06.20149.85 Mб45Курс высшей математики.pdf
#
13.06.20141.98 Mб46Курс лекций - Вычислительная математика.doc
#
13.06.20142.66 Mб74Лекции по математике 2 семестр.doc
#
13.06.2014279.55 Кб63Лекции по математике для экономистов.doc