1.2.2. Определение поверхности адсорбционной пленки

Поверхность адсорбционной пленки – это поверхность мезопор. Поверхность адсорбционной пленки может быть найдена по термодинамическому методу, предложенному А.В. Киселевым. Метод основан на использовании следующего термодинамического уравнения капиллярной конденсации:

(1.13)

где σ - поверхностное натяжение жидкого адсорбата при температуре опыта, Дж/м²; A_d – дифференциальная работа адсорбции, Дж/моль; a_S – максимальная величина адсорбции при P/Ps = 1, моль/г.

Численное значение интеграла находят графическим способом. Для этого, предварительно рассчитав дифференциальную работу адсорбции при различных относительных давлениях адсорбата P/Ps по уравнению:

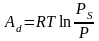(1.14)

строят графики зависимости A_d = f(a_адс.) и A_d = f(a_дес.) (рис. 1.2).

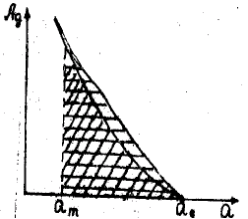
Рис. 1.2. Зависимость дифференциальной работы адсорбции от ее величины.

Путем графического интегрирования определяют площади под адсорбционной и десорбционной кривыми в интервале от a_m до a_S (в Дж/г) и среднее значение площади , которое численно равно интегралу в уравнении 13:

(1.15)

где S_a и S_d – площади, под адсорбционной и десорбционной кривыми соответственно.

Зная численное значение интеграла, рассчитывают поверхность адсорбционной пленки:

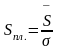(1.16)

1.2.3. Раздельное определение объемов микро- и мезопор

При адсорбции пара на пористом адсорбенте в начальные моменты, когда относительное давление паров мало, процесс идет обратимо до тех пор, пока на поверхности не образуется адсорбционная пленка определенной толщины. При этом микропоры заполняются жидким адсорбатом объемно. При повышении относительного давления начинается необратимый процесс капиллярной конденсации (рис.1. 3):

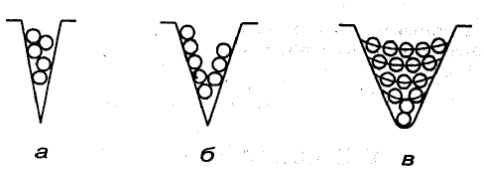
Рис.1.3. Объемное заполнение микропор (а) и стадии капиллярной конденсации (б, в).

В ходе капиллярной конденсации объемно заполняются мезопоры. Макропоры при адсорбции и капиллярной конденсации объемно не заполняются; поверхность их мала и адсорбированная на ней пленка не имеет большого объема, которым можно пренебречь. Поэтому можно считать, что объем жидкого адсорбата при P/P_S = 1 соответствует предельному суммарному объему микро- и мезопор V_Σ. Суммарный объем микро- и мезопор может быть рассчитан по уравнению:

(1.17)

где V – объем одного моля адсорбата (м³/моль); a_S – максимальная величина адсорбции при P/Ps = 1, моль/г.

Объемы микро- и мезопор находят по приближенному уравнению, предложенному Цицишвилли:

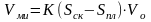(1.18)

(1.19)

где К – коэффициент, показывающий из скольких слоев состоит адсорбционная пленка к моменту начала гистерезиса; Vo – объем мономолекулярного слоя площадью в 1 м², (м³). Для приближенных расчетов предполагают, что К = 1. Тогда

где l– толщина адсорбционной пленки при мономолекулярном заполнении поверхности адсорбента адсорбатом, м:

(1.20)

где V – объем одного моля адсорбата (м³/моль); Sск – удельная поверхность скелета адсорбента, (м²/г).

1.2.4. Построение кривой распределения объема пор по радиусам

Для исследования пористой структуры адсорбентов и катализаторов применяются такие методы исследования как капиллярная конденсация и ртутная порометрия.

Метод капиллярной конденсации применим для изучения структуры мезопористых сорбентов. Сущность его заключается в следующем. Если для непористых и макропористых адсорбентов характерна моно- или полимолекулярная адсорбция газов, то в мезопористых адсорбентах адсорбция протекает по механизму капиллярной конденсации. При малых давлениях в мезопорах сначала образуется монослой или полислои адсорбата. Образующаяся в порах адсорбционная пленка адсорбата имеет вогнутую поверхность. Поскольку давление насыщенных паров над вогнутой поверхностью ниже, чем давление паров над плоской поверхностью, то в этих порах в дополнении к чисто адсорбционному процессу происходит капиллярная конденсация при P/P_S < 1.

Капиллярная конденсация – это процесс конденсации паров адсорбата в порах твердого тела.

Капиллярная конденсация начинается при таком значении адсорбировавшегося вещества, при котором образуется мениск жидкости с радиусом кривизны более 2-3 диаметров молекулы. В результате капиллярной конденсации происходит объемное заполнение пор жидким адсорбатом. Капиллярная конденсация описывается уравнением Томпсона – Кельвина:

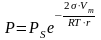(1.21)

где P – давление насыщенного пара над вогнутой поверхностью; P_S – давление насыщенного пара над плоской поверхностью; σ - поверхностное натяжение жидкого адсорбата; V_m – молярный объем жидкого адсорбата; r – радиус кривизны сферического мениска.

В уравнение Томпсона - Кельвина входит радиус кривизны мениска и это позволяет использовать его для расчета функции распределения пор по размерам.

Пористая структура адсорбента разнообразна, однако считается, что ее можно описать четырьмя видами пор: конусообразными, цилиндрическими с один или двумя открытыми концами и бутылкообразными. Для цилиндрических и бутылкообразных пор опорожнение пор при десорбции происходит при меньшем давлении, чем его заполнение. Этим объясняется появление петли капиллярно-конденсационного гистерезиса на изотерме адсорбции (рис. 1.4).

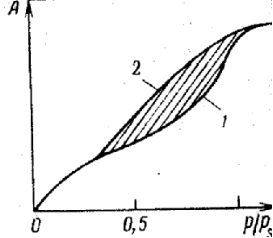
Рис. 1.4. Изотерма адсорбции при капиллярной конденсации:

1 – кривая адсорбции; 2 – кривая десорбции.

Адсорбции соответствует нижняя кривая, а десорбции – верхняя. При малых давлениях, когда не происходит капиллярная конденсация, гистерезиса не наблюдается. Для получения кривой распределения объема пор по радиусам используют десорбционную ветвь изотермы.

Каждой точке кривой десорбции соответствует определенное значение величины адсорбции и относительного давления. Эффективный радиус опорожняемых пор при данном относительном давлении рассчитывают из уравнения Томпсона-Кельвина:

(1.22)

Эффективные радиусы опорожняемых пор рассчитывают для различных относительных давлений, начиная с давлений, соответствующих заполнению мономолекулярного слоя.

При десорбции после опорожнения поры на ее поверхности остается адсорбционная пленка. Чтобы получить истинные радиусы пор, необходимо ввести поправку на толщину адсорбционной пленки:

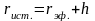(1.23)

где r_ист., r_эф. – истинный и эффективный радиусы соответственно; h – толщина адсорбционной пленки.

Толщину адсорбционной пленки можно рассчитать по уравнению Келси:

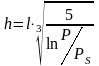(1.24)

где l – толщина мономолекулярного слоя, которая в свою очередь вычисляется по уравнению:

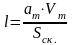(1.25)

Кроме радиусов опорожняемых пор необходимо рассчитать для тех же относительных давлений объемы опорожняемых пор. Эффективный объем пор, опорожняющихся при данном относительном давлении V_{пор, эф.}, равен произведению величины адсорбции на молярный объем абсорбата Vm:

(1.26)

В этот объем также надо включить поправку на объем адсорбционной пленки, который согласно уравнению Дубинина будет равен:

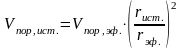(1.27)

Зная объем пор и соответствующие значения радиусов строят интегральную кривую распределения, типичный вид которой представлен на рис. 1.5.

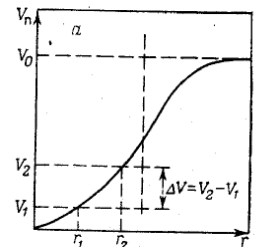
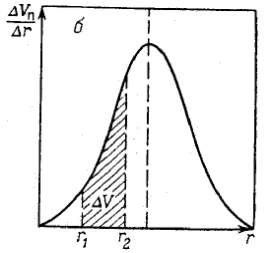
Рис. 1.5. Интегральная (а) и дифференциальная (б) кривые распределения объема пор по радиусам.

Чтобы избежать случайных погрешностей, интегральную кривую выравнивают (т.е. усредняют) и после этого с помощью графического дифференцирования строят дифференциальную кривую распределения. Каждая точка на интегральной кривой распределения, например, V₁ при r₁ дает объем пор с радиусами от r_min до r₁. По этой кривой можно определить объем пор ∆V =V₂ –V₁ с радиусами от r₁ до r₂ и общий объем пор V₀.

По дифференциальной кривой распределения объем пор (или долю от общего объема пор), размеры которого лежат в пределах от r₁ до r₂ определяется площадью, заключенной между осью абсцисс, дифференциальной кривой и ординатами r₁ и r₂. Чем резче выражен максимум и уже дифференциальная кривая, тем меньше различаются поры по размерам.

Из кривых распределения видно, что общий объем малых пор небольшой, однако доля поверхности, приходящаяся на эти поры, существенно большая. С увеличением размера пор объем растет быстрее, чем поверхность и в связи с этим максимум на дифференциальной кривой распределения сдвинут в сторону меньших радиусов. Построение кривых распределения позволяет более правильно представить структуру пористого тела, например, судить о полидисперсности.