Обработка полученных результатов

1. Определить постоянную калориметра. Для этого на миллиметровой бумаге построить график зависимости температуры от времени: Т = f(t) (рис. 10). Масштаб по оси абсцисс: 1 мин = 1 см. Масштаб по оси ординат: 0,1 0 = 1 см.

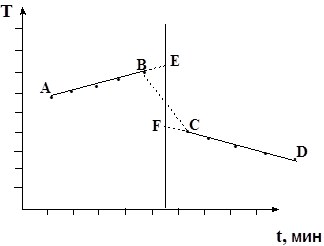
Рис. 10. График изменения температуры при растворении KCl.

Прямая АВ относится к начальному периоду, ВС – к главному, СD – конечному периоду. Точка В – последний отсчет начального периода, точка С – первый отсчет конечного периода. Через середину отрезка ВС провести перпендикуляр в оси абсцисс. Продолжить прямые АВ и CD до пересечением с перпендикуляром. Отрезок EF будет характеризовать действительное изменение температуры в опыте, т.е. ∆T. Крутизна наклона прямых АВ и CD зависит от характера теплообмена с окружающей средой. Определив ∆T, рассчитать постоянную калориметра W по уравнению 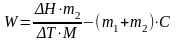5.5:

(5.5)

где m₁ и m₂ – масса воды и растворяемой соли соответственно; ∆H – молярная теплота растворения соли (для KCl ∆H = 18 841 Дж/моль); М – молярная масса растворяемой соли; С – удельная теплоемкость раствора (для раствора KCl С = 4,103 Дж/г·К).

2. Найти изменение температуры для суспензии исследуемого адсорбента ∆T расчетным способом:

(5.6)

где Т₂ – последний отсчет главного периода; Т₁ – последний отсчет начального периода; δ_Т – поправка на потерю тепла в окружающую среду.

Поправку δ_Т рассчитать по уравнению Щукарева (5.7):

(5.7)

где n - общее число интервалов главного периода;

Z₁ – среднее изменение температуры между двумя отсчетами в начальном периоде (разность первого и последнего отсчета, деленная на число измерений);

Z₂ – среднее изменение температуры между двумя отсчетами в конечном периоде (разность первого и последнего отсчета, деленная на число измерений);

Р – число первых интервалов главного периода, когда температура растет быстро ( не менее 0,003 ⁰);

y – число остальных измерений главного периода, когда температура растет медленно.

Если в конечном периоде температура не падает, а повышается, то Z₂ становится отрицательной величиной. Если температура в конечном периоде не изменяется, то Z₂ = 0.

3. Рассчитать удельную теплоту смачивания Q по уравнению 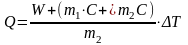(5.8):

(5.8)

где W – постоянная калориметра; m₁ и m₂ – масса воды и исследуемого образца соответственно; С – удельная теплоемкость исследуемого вещества.

4. Рассчитать теплоту смачивания 1 м² поверхности твердого тела q водой по уравнению 5.3 используя справочные данные, приведенные ниже.

5. Найти удельную поверхность исследуемого адсорбента, используя уравнение 5.4.

Таблица 5.1

Поверхностное натяжение воды на границе с воздухом при различных температурах

Температура, оС	 . 103, н/м	Температура, оС	 . 103, н/м
10	74,22.	21	72,59
11	74,07	22	72,44
12	73,93	23	72,28
13	73,78	24	72,13
14	73,64	25	71,97
15	73,49	26	71,82
16	73,34	27	71,66
17	73,19	28	71,50
18	73,05	29	71,35
19	72,90	30	71,18
20	72,75	35	70,38

Таблица 5.2

Удельные теплоемкости

№	Вещество	С, Дж/гК
1	Al2O3	0,774
2	SiO2	0,741

Контрольные вопросы и задания

1. Чем обусловлен тепловой эффект смачивания?

2. Что такое дифференциальная теплота смачивания?

3. Что такое интегральная теплота смачивания?

4. Для чего и в каком случае используют показатель теплоты смачивания?

5. Физический смысл термического коэффициента смачивания.

Лабораторная работа № 6.

Исследование процесса ограниченного набухания полимера

Краткие теоретические сведения

В отличие от процесса растворения низкомолекулярного вещества, при котором происходит в основном диффузия растворяемого вещества в растворитель, начальная стадия процесса растворения высокомолекулярных соединений (ВМС) заключается в диффузии молекул растворителя в объем полимера. Проникновение молекул растворителя в объем полимера сопровождается процессом набухания.

Растворение макромолекул обязательно проходит через стадию набухания, являющуюся характерной качественной особенностью веществ этого типа. При набухании молекулы растворителя проникают в твердый полимер и раздвигают макромолекулы. Последние, из-за своего большого размера, медленно диффундируют в раствор, что внешне проявляется в увеличении объема полимера. Набухание может быть неограниченным, когда конечным его результатом является переход полимера в раствор, и ограниченным, если набухание не доходит до растворения полимера.

Неограниченное набухание – это набухание, заканчивающееся растворением, когда полимер сначала поглощает растворитель, а затем при той же температуре переходит в раствор, образуя однофазную гомогенную систему. Так набухают каучуки в углеводородах, биополимеры в воде. Если растворение полимера останавливается на стадии набухания, то говорят об ограниченном набухании. Так, полимеры пространственного строения могут только ограниченно набухать, образуя студни. Ограниченно набухают полимеры, имеющие химические связи - мостики между молекулами, которые лишают полимер свойства текучести, не позволяют его молекулам оторваться друг от друга и перейти в раствор. Примером ограниченно набухающего полимера с мостиковыми связями между молекулами является вулканизированный каучук, в котором мостиками служат атомы серы или полярные группировки.

Процесс набухания с точки зрения термодинамики характеризуется уменьшением энергии Гиббса ∆G = ∆H ─ T∆ S < 0, и состоит из двух этапов или стадий.

1 стадия – энергетическая, характеризуется сольватацией (гидратацией) полимера: ∆Н < 0; ∆S ≈ 0. При этом |T∆ S| < | ∆H| , поэтому ∆G < 0 за счет уменьшения энтальпии (экзотермическая стадия).

2 стадия – энтропийная, характеризуется активным разрахлением сетки ВМС, увеличением объема полимера, поэтому энтропия возрастает, а энтальпия практически не меняется: ∆Н ≈ 0; ∆S > 0; T∆S > 0.

Уменьшение энергии Гиббса ∆G < 0 происходит за счет возрастания энтропии.

В случае полимеров линейного строения, при изменении условий (температуры, концентрации и др.) ограниченное набухание может перейти в неограниченное, т.е. в растворение полимера. При контакте полимера с растворителем начинается взаимная диффузия молекул растворителя в полимер, а макромолекул полимера − в растворитель. Однако скорость диффузии будет различаться в той же пропорции, что и размеры, а также подвижности диффундирующих частиц. Резкое различие в подвижностях молекул растворителя и макромолекул ВМС является причиной набухания.

Количественной мерой набухания является степень набухания α, которая может иметь объемное или массовое выражение:

(6.1),

где V₀, V, m₀, m – соответственно объемы и массы исходного и набухшего полимера.

На рисунке 6.1 приведена зависимость степени набухания от времени. Максимальная или равновесная степень набухания определяется природой полимера и растворителя, сродством между ними, густотой пространственной сетки полимера.

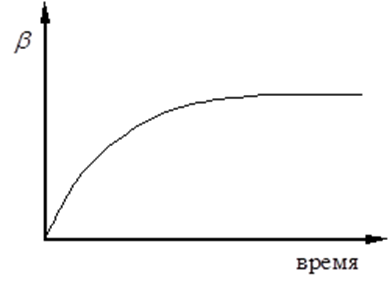
Рис.6.1. Зависимость степени набухания от времени.

Более точным является определение «α» по ее массовому выражению, так как в этом случае результаты измерений не зависят от явления контракции. Контракция заключается в том, что объем раствора (смеси) двух жидкостей оказывается меньше, чем сумма объемов взятых жидкостей.

В зависимости от структуры полимера и температуры набухание может быть ограниченным или неограниченным (рис. 6.2, а). При ограниченном набухании (рис. 3а, кривая 1) степень набухания достигает предельного значения, после чего набухание не зависит от времени (желатин в холодной воде). Для неограниченного набухания характерна зависимость (рис. 6.2 а, кривая 2), проходящая через максимум, после чего α падает до нуля в результате постепенного растворения полимера.

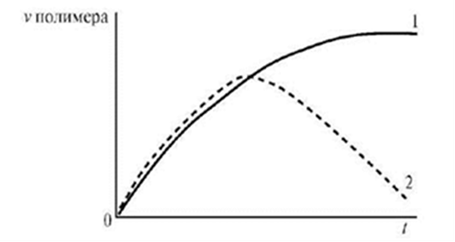
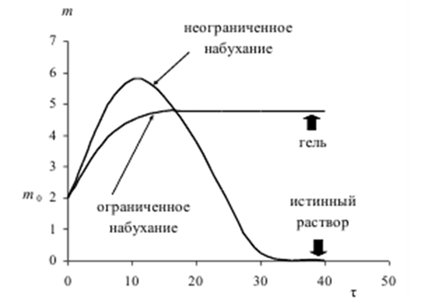
а б

Рис. 6. 2. Кинетика процесса набухания ВМС: а- кривые ограниченного (1) и неограниченного (2) набухания; б- кинетические кривые перехода полимера в гель и раствор.

Ограниченность или неограниченность набухания определяются соотношением энергий связей в полимере с энергией сольватации и энтропийным фактором. В линейных и разветвленных полимерах молекулы связаны ван-дер-ваальсовыми силами, энергия этих связей невелика, поэтому энергия сольватации и энтропийный фактор уже при комнатной температуре превышают их. При таких условиях набухание идет неограниченно. Если между цепями полимера имеются химические связи, то для их разрыва недостаточно бывает энергии сольватации и энтропийного фактора. Набухание протекает ограниченно, и полимер превращается в студень (рис. 6.2,б).

Набухание, как и сольватация, специфично, так как полимер набухает в растворителе, соответствующем его природе. В процессе набухания происходит односторонняя диффузия молекул растворителя в полимер. Это объясняется тем, что крупные макромолекулы, связанные в надмолекулярные структуры, практически не могут переходить в растворитель, а малые и хорошо диффундирующие молекулы растворителя легко проникают в полимер, увеличивая его объем. При набухании отдельные молекулы надмолекулярных структур сольватируются, межмолекулярное взаимодействие значительно ослабевает, в результате чего становится возможной диффузия макромолекул в растворитель (рис. 6.3).

Рис. 6.3. Взаимодействие растворителя с полимером: 1 – межструктурное набухание; 2 – внутриструктурное набухание; 3 – растворение.

Факторы, влияющие на процесс набухания

Процесс набухания имеет химическую природу и, следовательно, специфичен. Полимер набухает только в том растворителе, с которым он взаимодействует, поэтому полярные полимеры набухают в полярных жидкостях (белки в воде), неполярные - в неполярных (каучук в бензине).

Набухание не всегда кончается растворением полимера. Часто после достижения определенной степени набухания процесс прекращается либо из-за ограниченной растворимости ВМС в данном растворителе, либо из-за наличия в полимере поперечных химических связей, препятствующих отрыву макромолекул друг от друга и переходу их в раствор.

Набухание является экзотермическим процессом, поэтому в соответствии с принципом Ле Шателье, степень набухания увеличивается при уменьшении температуры. Однако скорость набухания при уменьшении температуры уменьшается, так как при более низких температурах диффузия протекает менее интенсивно.

С повышением температуры ограниченное набухание может переходить в неограниченное, т.е. полимер начинает растворяться. Начальная стадия процесса характеризуется положительным тепловым эффектом (выделяется теплота сольватации). В дальнейшем тепловой эффект ∆Н≈0, но зато возрастает энтропия за счет разрыхления сетки, и поэтому свободная энергия Гиббса остается отрицательной:

∆G = ∆H - T∆S < 0. (6.2)

Набухание твердого полимера в растворителе характеризуется степенью набухания (α), выраженной через массу образца ВМС до начала (m₀) и после завершения процесса (m):

(6.3)

Очевидно, что  численно равна массе жидкости, поглощенной 1г полимера. Процесс характеризуется также числом набухания n, представляющим собой отношение объема обработанного полимера к объему исходного образца:

(6.4),

где m₀ и m¹∞ - массы исходного образца и поглощенного им к концу процесса растворителя, ρ₀ и ρ - плотность полимера и растворителя, соответственно.

Определяя степень набухания образца ВМС через различные промежутки времени, получают кривые, характеризующие кинетику процесса. Аналитически эти кривые описываются кинетическим уравнением реакции первого порядка:

(6.5),

где К - константа скорости набухания, m¹_τ - количество растворителя, поглощенного образцом к моменту времени τ. Набухание в простейшем случае кинетически протекает как реакция первого порядка, потому что скорость процесса определяется скоростью диффузии растворителя в полимер.

Интегрируя уравнение (6.5), имеем:

(6.6)

Отсюда следует, что величину К можно определить графически, представив опытную зависимость m¹_τ, τ в виде прямой линии:

ln(m¹_∞ - m¹_τ) = ln(m¹∞) - K_τ, (6.7),

тангенс угла наклона которой определяет константу скорости набухания.

О влиянии природы растворителя на степень набухания можно судить по следующим данным, полученным для полистирола в органических жидкостях (α выражено в процентах): хлороформ – 1100, толуол – 1000, циклогексан – 100, гексан – 20, н-гексиловый спирт – 4.

Влияние поперечных связей в макромолекуле на способность к набуханию хорошо иллюстрирует пример с каучуком. Невулканизированный, т.е. не содержащий поперечных связей, каучук неограниченно набухает в углеводородах, образуя растворы. Вулканизированный каучук – резина, содержит поперечные сульфидные связи и набухает ограничено. Эбонит, представляющий собой каучук с очень «густой» пространственной сеткой, набухает значительно меньше. Степень набухания слабо вулканизированного каучука составляет 800-1000, а эбонита не более 150%.

Определяя степень набухания через заданные промежутки времени, можно получить кривые, характеризующие кинетику набухания. Скорость набухания различных полимеров можно сравнивать по наклону касательных, проведенных к кривым из начала координат, а способность полимеров к набуханию следует характеризовать по предельной степени набухания. На процесс набухания полимеров в воде влияет присутствие электролитов и значение рН среды. Влияние электролитов своеобразно прежде всего тем, что влияние оказывают в основном анионы, а катионы – лишь в незначительной степени. Причем одни анионы усиливают набухание, а другие ослабляют:

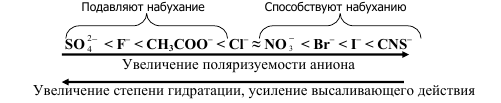
Влияние рН среды на набухание полимера больше всего проявляется в растворах белков, поскольку их молекулы – полиамфолиты.