Обработка результатов измерений

1. По калибровочному графику определить концентрацию вытекшего раствора толуола в н-гептане. Выразить концентрацию в мл/л.

2. Построить график зависимости концентрации вытекшего раствора от его объема (см. рис. 3.1).

Таблица

№	С, %	показатель преломления калибровочных раст-воров, d	объем вытек-шего раствора Vx, мл	показатель преломле-ния вытекающего раствора, dx

Рис. 3.1. Выходная кривая

Заштрихованная площадь на выходной кривой пропорциональна количеству адсорбированного толуола при полном насыщении слоя; V_г – объем чистого вытекшего н-гексана.

3. Рассчитать адсорбционную активность силикагеля по уравнению (1.28).

4. Методом графического интегрирования найти площадь заштрихованной фигуры.

5. Рассчитать величину равновесной адсорбции толуола по уравнению:

(1.29)

где S – площадь заштрихованной фигуры; K – коэффициент пропорциональности, равный произведению масштаба по оси абсцисс на масштаб по оси ординат. Например, на приведенном графике K = 5•10^-2; ρ - плотность толуола; m – масса силикагеля.

II. Поверхность раздела твердое тело - жидкость

2.1. Межфазные взаимодействия между конденсированными фазами.

К межфазным взаимодействиям между конденсированными фазами относятся смачивание/несмачивание, растекание, адгезия и когезия.

Адгезией (от лат. adhaesio — прилипание) называют межфазное взаимодействие между поверхностями конденсированных фаз при их молекулярном контакте. Работа адгезии Wa — это работа обратимого разрыва адгезионной связи между двумя фазами, отнесенной к единице площади. При этом происходит образование новых поверхностей раздела каждой из этих фаз с воздухом (на это затрачивается энергия (σ_жг + σ_тг)) и разрушение границы раздела контактировавших фаз (– σ_тж). В результате работа адгезии в системе ж/т :

Wa = σ_ЖГ+ σ_ТГ – σ_ТЖ (2.1)

Это уравнение (уравнение Дюпре) отражает закон сохранения энергии при адгезии. В этом случае энергия затрачивается на образование двух поверхностей раздела, равных по величине, но разных по свойствам. Соответственно, изменения свободной энергии связаны с заменой свободной энергии исходной межфазовой границы на свободную энергию поверхностей фаз, граничащих с собственным паром.

Работу адгезии можно рассматривать как меру интенсивности взаимодействия двух разных контактирующих фаз, т.е. степени взаимного насыщения нескомпенсированных поверхностных сил, причем член σ_тж определяет интенсивность остаточных нескомпенсированных связей ( чем больше σ_тж, тем меньше при прочих равных условиях величина Wa).

В отличие от адгезии, которая характеризует взаимодействие между поверхностями разных фаз, когезия отражает связь внутри одной фазы, характеризуя прочность конденсированной фазы и способность тел противодействовать внешнему усилию. Работу когезии Wk определяют как работу разрыва однородной гомогенной фазы с образованием двух новых поверхностей раздела этой фазы с ее собственным паром. В простейшем случае, работа когезии (Wk) определяется затратой энергии на обратимый изотермический разрыв фазы, отнесенной к единице площади:

Wk = 2σ_ЖГ (2.2),

где множитель 2 указывает на образование двух новых одинаковых по величине и свойствам поверхностей раздела ж/г. В итоге работу когезии можно рассматривать как меру межмолекулярного взаимодействия в объеме гомогенной конденсированной фазы.

Соотношение между работами адгезии и когезии можно выразить с помощью следующих уравнений:

Wa /Wk = 0.5 ( 1 + Cos θ ) (2.3)

или

Wa = σ_ЖГ (1+ Cos θ) (2.4)

Уравнение (2.4) удобно тем, что позволяет исключить трудно определяемые экспериментально величины σ_ТГ и σ_ТЖ, в то время как значения σ_ЖГ и Cosθ измеряются довольно легко.

В зависимости от соотношения между силами адгезии между жидкостью и твердым телом и силами когезии внутри жидкости возможны следующие результаты при нанесении небольшого количества жидкости на поверхность твердого тела: несмачивание, смачивание и растекание.

Смачивание – поверхностное явление, которое возникает в результате взаимодействия жидкости с твердым телом или другой жидкостью при наличии одновременного контакта с воздухом. Общая граница контакта трех фаз называется линией смачивания.

Количественной характеристикой смачивания является краевой угол (θ) – угол между касательной к поверхности капли и смачиваемой поверхностью (рис. 2.1), причем вершина угла лежит на линии смачивания. Краевой угол θ отсчитывается в сторону жидкости, а при избирательном смачивании – в сторону более полярной из двух жидкостей.

Рис. 2.1. Схема смачивания жидкостью поверхности твердого тела: а – капля жидкости на смачиваемой поверхности (δ < 90°); б – капля жидкости на несмачиваемой поверхности (δ > 90°).

Чем меньше краевой угол, тем выше смачивание и наоборот. Величина смачивания определяется результатом конкуренции сил межмолекулярного притяжения внутри жидкости (сил когезии) и сил молекулярного взаимодействия между жидкостью и твердым телом (сил адгезии).

В зависимости от молекулярной природы жидкости и твердого тела могут наблюдаться три частных случая.

1. Если молекулы жидкости взаимодействуют с молекулами твердого тела сильнее, чем между собою, то капля растекается по поверхности, образуя мениск с острым краевым углом (0° < θ < 90°) (см. рис. 4,а) или

тонкую пленку с краевым углом θ = 0°. Последний случай (θ = 0°) называется полным смачиванием (вода на обезжиренной поверхности стекла или кварца).

2. Если же молекулы жидкости взаимодействуют друг с другом сильнее, чем с молекулами твердого тела, то капля стягивается, образуя тупой краевой угол θ > 90° (см. рис. 4,б), как в случае воды на парафине или фторопласте. Случай θ = 180° (полное несмачивание) является гипотетическим, т.к. он означал бы полное отсутствие молекулярного взаимодействия между фазами, что нереально.

3. Между этими крайними случаями наблюдаются различные промежуточные, когда капля жидкости образует с поверхностью краевой угол θ, который является мерой смачивания (рис.2.1,а).

По измерению краевого угла все поверхности делятся на две группы: гидрофильные и гидрофобные. Если вода на твердой поверхности образует угол 0° < θ < 90°, то такую поверхность называют гидрофильной, если угол θ > 90° , то поверхность является гидрофобной.

Тела, для которых в условиях избирательного смачивания краевой угол θ < 90^о (Cos θ > 0), называются гидрофильными, а в обратном случае (θ > 90^о, Cos θ < 0) – гидрофобными (или олеофильными).

Гидрофильными телами являются, например, оксиды и гидроксиды металлов, большинство неорганических солей – силикаты, сульфаты, карбонаты и др., из органических соединений гидрофильна целлюлоза (благодаря наличию в структуре макромолекулы большого количества полярных ОН- групп).

К гидрофобным телам относятся органические вещества с большим содержанием СН-связей (парафиновые и ароматические углеводороды, вещества с полярными группами, но большим углеводородным радикалом, например, средние и высшие жирные кислоты). Из неорганических веществ гидрофобны сера, графит, многие сульфиды, чистые металлы.

Смачивание можно рассматривать как процесс, при котором в системе из трех соприкасающихся фаз происходит уменьшение свободной поверхностной энергии. Если удельная свободная поверхностная энергия на границе твердого тела и жидкости меньше, чем на границе твердого и газа (σ_ТЖ < σ_ТГ), то энергетически выгодно растекание жидкости (смачивание), при котором поверхность с высокой энергией частично заменяется на поверхность с меньшим запасом свободной энергии. И наоборот, если σ_ТЖ > σ_ТГ , то энергетически выгодно несмачивание.

Условие равновесного смачивания выражается уравнением Юнга:

σ_ТГ = σ_ТЖ + σ_ЖГ cosθ (2.5)

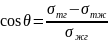(2.6)

Из уравнения Юнга вытекают некоторые следствия:

1) Различные жидкости тем лучше смачивают данную твердую поверхность, чем ниже поверхностное натяжение жидкости.

2) Смачиваемость твердых тел тем больше, чем выше их свободная поверхностная энергия. Поэтому, в общем, смачиваемость повышается в ряду: тела с молекулярной кристаллической решеткой < с полярными связями < с ионной кристаллической решеткой.

Парафин, сера, уголь смачиваются хуже, чем оксиды, соли, силикаты.

3) При избирательном смачивании из двух жидкостей смачивать данную твердую поверхность будет та, полярность которой ближе к полярности твердого тела. Другими словами смачивающей будет та жидкость, у которой меньше разность полярностей с данным твердым телом, т.е. она более близка к нему по молекулярной природе, проявляет более сильное межмолекулярное взаимодействие с ним и обеспечивает, следовательно, более низкое значение величины σ_ТЖ.

Из уравнений (2.3-2.4) также следует:

при θ= 0⁰ Cos θ = 1.0 Wa /Wk = 1.0 (полное смачивание),

90⁰ > θ > 0⁰ 1> Cos θ > 0 0.5 < Wa /Wk < 1.0 (смачивание),

θ= 90⁰ Cos θ = 0 Wa /Wk = 0.5 (равновесие)

180⁰>θ >90⁰ 0> Cos θ > -1 0 < Wa /Wk < 0.5 (несмачивание)

При равенстве работ когезии и адгезии контактный угол θ=0⁰, а условие Wa/Wk > 1.0 приводит к неограниченному растеканию (это же условие является необходимым условием последующего растворения). Движущую силу растекания определяют как разницу работ адгезии и когезии и называют работой растекания.

Неограниченное растекание жидкости. Как отмечено выше, положительное или отрицательное смачивание зависит от соотношения работ адгезии и когезии смачивающей жидкости. При полном смачивании (Wа = Wk) жидкость образует на поверхности тонкую пленку (в пределе – мономолекулярную), при этом краевой угол θ = 0°. Возможен случай, когда жидкость обладает столь высоким молекулярным сродством к поверхности («фильностью»), что адгезионные силы будут превышать силы когезии (Wа > Wk), и тогда происходит процесс, называемый неограниченным растеканием жидкости: ее межмолекулярные связи разрушаются в результате адгезии, и поверхностная пленка переходит из жидкого в газообразное состояние: молекулы жидкости занимают всю доступную поверхность, подобно тому, как газ занимает весь объем сосуда (происходит поверхностное испарение). Величина f = Wа – Wk называется коэффициентом растекания (коэффициентом Гаркинса). Его можно выразить через величины поверхностного натяжения, подставляя значения Wа и Wk:

f = (σ_ТГ + σ _ЖГ – σ_ТЖ) – 2 σ _ЖГ = (σ_ТГ – σ _ТЖ ) - σ_ЖГ = σ_ЖГ·cosθ - σ_ЖГ

f = σ_ЖГ (cosθ - 1) (2.7)

При отрицательных значениях f происходит ограниченное растекание с установлением конечного значения краевого угла. Условие неограниченного растекания: f > 0.

Величина адгезии всегда больше нуля, т.к. между соприкасающимися фазами всегда имеется какое-либо, пусть очень небольшое межмолекулярное взаимодействие. Поэтому ситуация, когда Wa=0 и угол θ=180⁰, невозможна.

Тепловой эффект смачивания обусловлен межмолекулярным взаимодействием на границе Т/Ж, в результате которого при нанесении жидкости на твердое тело происходит убыль не только свободной поверхностной энергии, но и полной поверхностной энергии (поверхностной энтальпии). Межмолекулярное взаимодействие тем сильнее, чем меньше разность полярностей жидкости и твердого тела. Поэтому тепловой эффект смачивания гидрофильных тел водой больше, чем углеводородами и наоборот – для гидрофобных тел он ниже, чем при смачивании их углеводородами. Различают дифференциальную и интегральную теплоты смачивания.

Дифференциальная теплота смачивания λ_d – теплота, выделяющаяся при нанесении бесконечно малого количества жидкости на поверхность, уже содержащую некоторое количество жидкости (слой толщиной x). Эта теплота максимальна при x = 0 и убывает до λ_d = 0 при некоторой толщине x = h, равной расстоянию, на котором интенсивность поля ненасыщенных молекулярных сил поверхности спадает до нуля. Ее относят к 1 моль смачивающей жидкости: [λ_d] = Дж/моль.

Интегральная теплота смачивания λi - теплота, выделяющаяся при

нанесении некоторого конечного количества жидкости x на исходную

(сухую) поверхность:

λi = 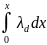(2.8)

При x → h величина λi возрастает до λi = λmax ,где λmax – полная интегральная теплота смачивания, отвечающая полному заполнению поверхностного слоя с единичной площадью: [λi] = Дж/м².

Теплоты смачивания используют для оценки поверхностных молекулярных свойств тела и количественной характеристики смачиваемости, когда невозможно экспериментально определить значение краевого угла: в случае порошкоообразных, волокнистых, пористых тел. Чтобы избежать измерений межфазной поверхности таких тел, в качестве термической характеристики смачиваемости используют отношение полных теплот смачивания тел водой и углеводородом:

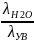= β (2.9)

где λ_H2O и λ_УВ - полная интегральная теплота смачивания водой и углеводородом, соответственно; β - термический коэффициент смачивания. Если β > 1, то тело гидрофильно, при β < 1 тело гидрофобно.