13 Косвенные измерения. Определение. Алгоритм обработки результатов косвенных измерений. Вычисление точечных оценок результата косвенных измерений. Пример.

Косвенное измерение  определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной. Примером косвенных измерений может быть измерение плотности цилиндрического тела ( = m/v), измерение удельного сопротивления проводника электрическому току, измерение сопротивления методом амперметра-вольтметра (R = U/I). Погрешность косвенных измерений, как правило, больше погрешности прямых измерений, что является их недостатком. Это связано с двумя причинами: измерением нескольких величин и использованием приближённых значений физических констант. Зато с помощью косвенных измерений можно измерить такие величины, которые принципиально невозможно (плотность вещества) или нерационально (площадь земельного участка) измерять прямо. Это  достоинство косвенных измерений. При обработке результатов косвенных измерений нужно помнить что они являются функциями случайных величин. Обращение с результатами измерений как не с СВ вызывает появление ошибок. Особо сложным случаем является обработка функции 2х не нормально распределенных величин. В этом случае закон распределения функции будет отличаться от законов распределения аргументов. Пусть выполняют косвенные измерения величины Z путем вычисления ее значений по результатам прямых измерений величин х и у. Для вычисления используют функциональную зависимость . Пусть величина Х характеризуется точечными оценками.Точечные оценки результата косвенных измерений Z получают путем приближенного вычисления. Для этого функциональная зависимостьраскладывается в ряд Тейлора бесконечный ряд с убывающими значениями.

Наибольшую весомость имеют первые 3 слагаемые ряда:-1ое характеризует среднее значение результата косвенных измерений. -2ое характеризует стандартное отклонение результата косвенных измерений.R-коэффициент корреляции величин ХиУ.R учитывает наличие взаимосвязи между ХиУ. Если между величинами существует функциональная связь то =1. Если величины независимы друг от друга то=0. Если между величинами существует случайная связь то 0<<1Из-за особенности ряда Тейлора результат косвенных измерений всегда оказывается больше Z на величину 3-го слагаемого ряда поэтому в результат косвенного измерения вносят поправку числено равную 3-му слагаемому но с противоположным знаком.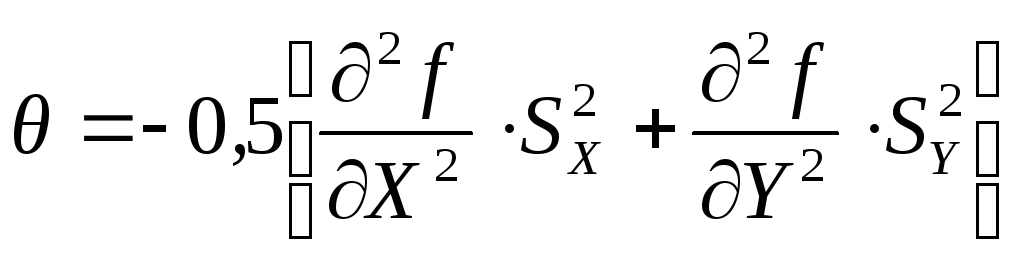Результат косвенных измерений записывают в виде неравенства .Р=,,, n=…. E=t^*·S, где t^* коэффициент надежности определяемы по числу степеней свободы результата

14 Обработка экспериментальных данных при изучении зависимостей. Сущность метода наименьших квадратов, условия его применения. Алгоритм построения зависимости по экспериментальным данным методом наименьших квадратов.

При проведении экспериментальных исследований МХ преобразователей, часто возникает потребность в построении их градуировочных характеристик. Для этого используют несколько методов. Выбор метода зависит от количества информации, которой располагает экспериментатор.

1. Если известно, что входная величина задана абсолютно точно для каждой экспериментальной точки, а выходная величина подчиняется нормальному закону распределения, то используют метод наименьших квадратов.

Это упрощённый вариант метода максимального правдоподобия, который предполагает многократное измерение выходной величины в каждой экспериментальной точке.

2. Если погрешностью входной величины пренебречь нельзя, то используют метод конфлюэнтного анализа.

3. Если значение входной величины известно точно, а значение выходной величины не подчиняется нормальному закону – используют робастные (устойчивые) методы.

Эти методы (робастные) помогают подогнать закон распределения выходной величины под нормальный закон.

Построение градуировочных характеристик методом наименьших квадратов

1. Строят график экспериментальной зависимости в виде точек

2. По виду последовательности точек определяют начальный вид уравнения регрессии (обычно это уравнение прямой), т.е.

3. Определение параметров уравнения регрессии. Параметры предложенного уравнения нужно определить так, чтобы погрешность, с какой линия описывает экспериментальные данные, была бы минимальной. При этом руководствуются положениями:

1. Каждая точка несёт информацию о зависимости и далее учитывается в равной степени по сравнении с другими точками.

2. Каждая точка содержит погрешность измерения.

Для определения параметров уравнения регрессии используют метод наименьших квадратов. Он заключается в том, что оптимальной кривой регрессии считают такую, для которой сумма квадратов отклонений экспериментальных значений от расчётных, будет минимальной, т.е.

Это условие будет выполнятся если:

Поэтому для определения параметров уравнения регрессии коэффициентов a и b составляют систему уравнений, в которой частные производные приравниваются к нулю, затем из этой системы находят формулы для вычисления параметров.

Например, для линейного уравнения регрессии система уравнений имеет вид:

– решить систему уравнений и определить неизвестные параметры, например, для линейного уравнения регрессии решение имеет вид:

.

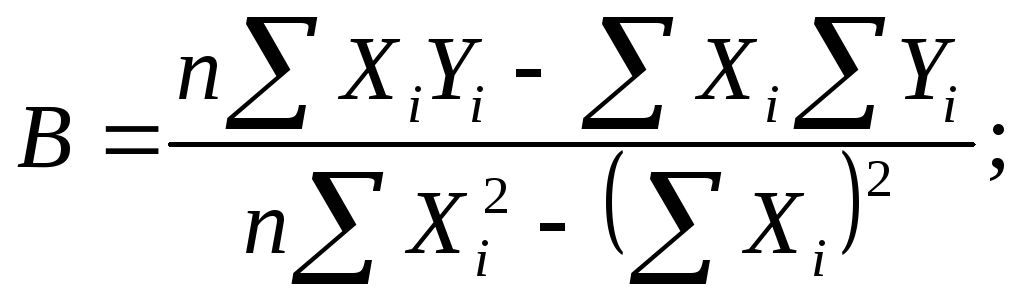
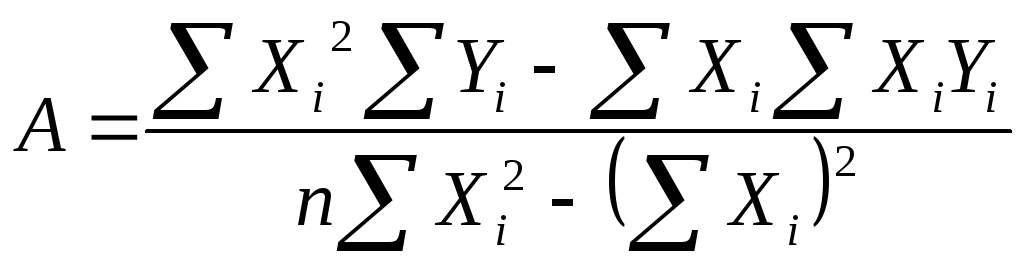4. Проверка правильности выбора уравнения регрессии и расчёта его параметров.

На этом этапе определяют, достоверно ли экспериментальные данные описываются уравнением, считается, что уравнение достоверно описывает данные, если в последовательности отклонений отсутствуют тренды (смещения). Тренды могут быть:

1. Аддитивные (экспериментальные точки выше кривой регрессии)

2. Мультипликативные (экспериментальные точки выше и ниже кривой регрессии)

3. Колебательные (в виде параболы пересекающей кривую регрессии)

Отклонения бывают случайными или систематическими (содержать тренды). Если в последовательности отклонений тренды отсутствуют, то гипотеза о выборе уравнения регрессии сделана верно.

Для выявления трендов используют критерий серий и инверсии:

– рассчитать отклонения экспериментальных значений Y_i от соответс­твующих значений Y_pi, рассчитанных для того же аргумента X_i по полученному уравнению регрессии:

Y_i = Y_i – Y_pi ;

– построить в осях координат X, Y полученные значения Y_i для со­ответствующих X_i;

– записать последовательность значений Y_j по мере возрастания X_j, X_j  [l,n];

– рассчитать число серий N в полученной последовательности Y_j (под серией в данном случае понимают последовательность отклонений одного знака, перед и после которой следуют отклонения противоположного знака или нет вообще никаких отклонений);

– задавшись доверительной вероятностью Р ( уровнем значимости  = 1 – Р) для n = 20 определить по соответствующей таблице (таблица А.6 [4] или таблица Ж.1) допустимые границы N_1-0,5 и N_0,5;

– рассчитать число инверсий А в полученной последовательности Y_j (под инверсией понимается событие, заключающееся в том, что Y_j > Y_jk при k > j):

,

где A_j – это число инверсий j - гo члена последовательности, т.е. число членов последовательности, которые, будучи расположенными в последовательности после j - ого члена, имеют значение меньшее, чем DY_j;

– задавшись доверительной вероятностью Р ( уровнем значимости  = 1 – Р) для n = 20 определить по соответствующей таблице (таблица А.7 [4] или таблица И.1) допустимые границы A_1-0,5 и A_0,5;

– сравнить А с A_1-0,5 и A_0,5;

Если выполняются неравенства

N_1-0,5 < N  N_0,5;

A_1-0,5 < A  A_0,5,

то с выбранной доверительной вероятностью Р можно считать, что отклонения экспериментальных значений Y_i, от соответствующих значений Y_рi найденного уравнения регрессии являются случайными, не содержат аддитивного, мультипликативного или колебательного трендов, т.е. рассчитанное уравнение регрессии достоверно описывает экспериментально исследуемую зависимость между величинами X и Y.

Если хотя бы одно из указанных выше неравенств, не выполняется, то следует пересмотреть выбор вида уравнения регрессии. В частности, можно увеличить степень полинома m на единицу и повторить вычисления по описанному выше алгоритму. Например, для полинома второй степени:

Y = А + В∙Х + С∙Х².

С целью определения параметров уравнения регрессии в данном случае необходимо решить систему уравнений: