10 Однократное измерение. Особенности метрологического анализа однократного измерения. Алгоритмы обработки результата однократного измерения.

Особенности метрологического анализа однократного измерения заключаются в следующем:1.из множества возможных значений отсчета получается только одно (и используется);2.представление о законе распределения вероятности отсчета и его СКО формируется исключительно на основе априорной информации.Порядок действий при однократном измерении: 1.Предварительно проводят тщательный анализ априорной информации. Уясняется физическая сущность объекта измерений, уточняется его модель, устанавливаются влияющие факторы и принанимается решение о мерах по уменьшению влияния этих факторов (термостатирование, экранирование, компенсация полей). Определяются значения поправок, выбирается метод и средства измерения, разрабатывается методика измерений. Анализируется опыт подобных измерений в прошлом. Одним из итогов анализа априорной информации является вывод о достаточной точности однократного измерения для решения измерительной задачи. 2. Получение одного значения отсчета – основная измерительная процедура. Отсчет является случайным значением измеряемой величины и не может полностью характеризовать ее.3.Получение одного значения показания Х средства измерения. Имеет ту же размерность, что и измеряемая величина. 4.Определение пределов, в которых находится значение измеряемой величины. Зная класс точности средства измерения, определяют предельную допустимую абсолютную погрешность и пределы в которых лежит значение измеряемой величины:;5.Внесение суммарной поправки. Осуществляется на основе анализа особенностей метода измерений и условий, в которых оно выполнялось. Поправка смещаетQ₁ и Q₂, устанавливает пределы измеряемой величины. В качестве априорной информации может использоваться и опыт подобных измерений в прошлом. В конечном счете, необходимо знать закон распределения вероятности результата измерения и СКО. Показания могут подчиняться, например равномерному закону (из-за наличия люфтов) или нормальному закону. Во всех этих случаях значение измеряемой величины без учета поправки не отличается от случайного показания средства измерения Х больше, чем на половину доверительного интервала (нормальный закон) или на полуразмах (равномерный закон).Поправка при однократном измерении всегда вносится на последнем этапе.

11 Прямое многократное измерение. Особенности метрологического анализа многократного измерения. Алгоритмы обработки результата многократного измерения.

Многократное измерение проводится в основном в профессиональной метрологической деятельности а также при проведении точных измерений научных экспериментов. Они очень трудоемки и требуют затрат времени и средств, поэтому необходимость многократного измерения должна быть технико-экономически обоснована.Рассмотрим последовательность действий при проведении многократного измерения. 1.Анализ априорной информации. Назначение анализа такое же, как при однократном измерении. При этом роль анализа в данном случае уменьшается за счет большого количества апостериорной информации, получаемой в процессе измерений (распределение вероятности результата измерений определяется экспериментально). 2.Получение n независимых значений отсчета. Эта основная измерительная процедура, которая может быть организованная по-разному: Если измерением измеряемой величины во времени можно пренебречь, то значения отсчета получают путем многократного повторения процедуры сравнения; Если известно, что измеряемая величина может существенно измениться, то ее измеряют одновременно несколькими средствами измерений, каждое из которых дает одно из значений отсчета. 3. Перевод значений отсчета в показания и внесение в них поправок. В результате этого действия получают n независимых результатов измерений. Если многократное измерение выполнялось одним средством измерения, то поправки могут изменяться за счет изменения во времени влияющих факторов. Если использовалось несколько средств измерений, то поправки отличаются из-за индивидуальных свойств средств измерений. Весь массив данных (гдеi=1..n) характеризует результат многократного измерения. 4.Исключение ошибок. Определяют точечные оценки результата измерения и проверяют по правилу «трех сигм» (или иначе) сомнительные результаты. Если ошибки есть, то их исключают и повторно определяют точечные оценки (способ ранее рассмотрен). 5.Проверки нормальности закона распределения вероятности результата измерения. Дальнейшая обработка результатов измерений производится в зависимости от того, является ли закон распределения вероятности нормальным или нет.5.1Строят гистограмму. По виду гистограммы уже можно определить, что закон распределения отличается от нормального закона. Если по гистограмме можно предположить что закон может быть нормальным эту гипотезу нужно математически доказать. При построении гистограммы учитывают следующие рекомендации:интервалы по оси абсцисс следует выбирать, по возможности одинаковыми; число интервалов зависит от n; масштаб гистограммы целесообразно выбирать так, чтобы ее высота относилась к основанию как ½. 5.2 Проверка нормальности закона распределения по критерию Пирсона. Выдвигают гипотезу о том, что экспериментальные данные соответствуют нормальному закону. За меру расхождения экспериментальных данных с теоретическим законом принимают сумму квадратов отклонений отношения m/n от теоретической вероятности p_i попадания отдельного значения в i-тый интервал (m – число результатов измерения в i-том интервале; n – число всех результатов измерения), причем каждое слагаемое умножают на коэффициент n/p_i: , гдеk – число интервалов; n – число результатов, попавших в i-тый интервал; p_i – вероятность попадания отдельного результата в i-тый интервал. Если расхождение случайно, то χ² (коэффициент «ХИ-квадрат» или «коэффициент Пирсона») подчиняется распределению Пирсона. По этому распределению есть необходимые таблицы. По таблицам в зависимости от доверительной вероятности и числа интервалов можно определить табличный коэффициент χ₀². Если χ²< χ₀² ,то с установленной вероятностью можно признать случайным расхождение экспериментальных данных и теоретического закона распределения, что подтверждает гипотезу о выбранном теоретическом законе. Последовательность действий при проверке следующая: разбивают диапазон изменения Q на интервалы (5-30) так, чтобы в каждом интервале было не менее 5 значений; определяют значения t_i для каждого i-ого интервала по формуле: , гдеQ_i – наибольшее значение для i-ого интервала; определяют значение интеграла вероятности Лапласа L(t_i) для каждого i; определяют ; определяют; определяют χ², сравнивают его с табличным значением χ₀²; делают заключение о законе распределения результата измерения. Критерий согласия Пирсона широко применяется при n=40..50 и более. 5.3 Проверка нормальности закона распределения по составному критерию. Применяют при 10..15<n<40..50. Рассчитывают критерий по формуле: . Проверяют выполнение условия:, гдеd_min и d_max – коэффициенты, зависящие от вероятности P₁^*, с которой принимают решение. Они определяются по соответствующим таблицам. Если условие выполняется, то дополнительно проверяют «хвосты» теоретического и эмпирического распределения. При 10<n<20 считается допустимым отклонение одного из результатов Q_i от среднего арифметического больше, чем на 2,5S_Q; при 20<n<50 – двух, что соответствует доверительной вероятности P₁^**=0.98. Несоблюдение хотя бы одного из этих условий достаточно для того, чтобы гипотеза о нормальности распределения была отвергнута. В противном случае гипотеза принимается с вероятностью .5.4 Решение принимается на основе априорной информации. Приn<10 гипотеза о нормальности закона распределения вероятности результата измерения не проверяется. 6. Определение доверительного интервала. 6.1При нормальном законе распределения вероятности результата измерения доверительный интервал определяется, как изложено в п.1.9.4: при n>40..50 определяется через функцию вероятности; при n<30..40 – по распределению Стьюдента. 6.2.При отклонении гипотезы о нормальности закона распределения по виду гистограммы можно выдвинуть гипотезу хотя бы о симметричности закона. Гипотезы о симметричности закона распределения проверяются по тем же критериям. При этом в качестве теоретического закона выбирают одну из стандартных аппроксимирующих функций, вид которой можно определить по гистограмме или по априорной информации.Особенность стандартных аппроксимирующих функций заключается в том, что они усеченные. Поэтому смысл доверительного интервала для них теряется. Вместо него по «МИ 1317-86 ГСИ. Результаты измерений и характеристики погрешностей измерений. Формы представлений …» используется аналог доверительного интервала, определяемый как ±a·S, где a – аналог коэффициента t, он берется из соответствующих таблиц. В случае, когда по гистограмме явно видно, что закон распределения несимметричный, то поступают следующим образом: устанавливают пределы, за которыми не может оказаться значение измеряемой величины при любом законе распределения (точность при этом, конечно, ниже). Для несимметричных законов среднее арифметическое и СКО уже не являются оценками результата измерения как ранее. Неравенство Чебышева устанавливает, что вероятность того, что значение случайного числа при любом законе распределения не будет отличаться от среднего значения больше, чем на половину доверительного интервала:

В данном случае S определяется как:. По таблице определяют для доверительной вероятности значениеt, по которому вычисляют доверительный интервал. Если закон не нормальный, но симметричный, то значение можно оставить прежним (как при нормальном законе). Неравенство Чебышева в данном случае будет иметь вид:.При этом точность измерения более высокая.

12 Обработка результатов нескольких серий измерений. Понятия «серия измерений», «однородная» и «неоднородная» серии измерений. Алгоритмы обработки результатов нескольких серий измерений.Часто возникают ситуации, когда многократное измерение одной и той же величины производится в несколько этапов, разными людьми, в разных местах, в разное время и на разных приборах. Результат такого измерения необходимо определять путем обработки нескольких серий результатов, которые могут отличаться по статистическим характеристикам.Серии называют однородными, если результаты в них подчиняются одному и тому же закону распределения вероятности. В противном случае серии считаются неоднородными.Обработка результатов нескольких серий зависит от того, однородны они или нет. Поэтому при задании способа обработки результатов обязательно производят проверку однородности серий.Обычно сравнивают средние арифметические и оценки дисперсий в каждой серии. Проверка производится в 2 этапа:1.проверка значимости различия между средними арифметическими; 2.проверка равно рассеянности результатов измерений в сериях. 1.При проверке значимости различия между средними арифметическими вначале проводят обработку данных в каждой серии отдельно. При этом определяют значения средних арифметических (и), СКО (и) для каждой серии; производят проверку нормальности закона распределения. Затем определяют моменты закона распределения разностиG . Среднее, СКО, гдеn1 и n2 – число результатов в первой и второй сериях. Если n1+n2>20..30, то, задавшись доверительной вероятностью p, по таблицам для нормального распределения определяют t и вычисляют доверительный интервал, как . РазностьG не может оказаться за пределами этого интервала, если она является случайной и распределена по нормальному закону. Если выполняется условие: , то различия между средними арифметическими в сериях незначимы. 2. При проверке равно рассеянности результатов измерения в двух сериях после вычисления среднего арифметического и СКО для каждой серии и проверки нормальности результатов измерений в сериях определяют отношение дисперсий:, которое подчиняется распределению Фишера. Задаются вероятностьюP с которой принимается решение. По соответствующим таблицам определяют для выбранной вероятности P, значений n1 и n2 значение аргумента интегральной функции распределения вероятности Фишера ψ₀. Если выполняется условие , то серии считаются равно рассеянными, если не выполняется – то серии считают неравно рассеянными. Равно рассеянные серии с незначимым различием между средними арифметическими считаются однородными. Если полученные экспериментальные данные определены в одних и тех же условиях, то говорят о сходимости измерений, если в разных – то о воспроизводимости измерений. Экспериментальные данные однородных серий обрабатывают как единый массив. Для сокращения вычислений применяют формулы:

При обработке неравно рассеянных серий с незначимо различающимися средними арифметическими особенно ценные измерения учитываются с большей точностью. Последовательность обработки данных следующая: определяют среднее арифметическое в каждой серии (j – число серий); определяют СКО среднего в каждой серии S_j; определяют стандартное отклонение среднего взвешенного: 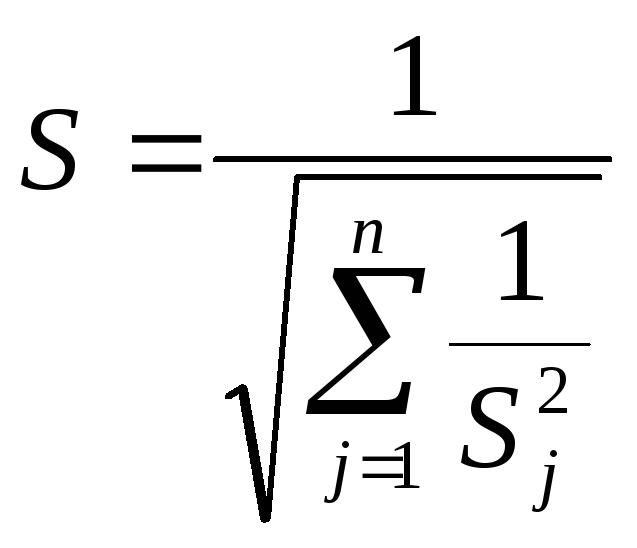, гдеn – число серий (n=1..j). определяют среднее взвешенное: ; задаются доверительной вероятностьюP; определяют n₀ по таблицам t и рассчитывают доверительный интервал, как ; записывают результат измерения. При обработке неравнорассеянных серий со значимым различием средних арифметических результаты измерений в каждой серии обрабатывают отдельно. При этом обработку проводят по правилам обработки результата многократного измерения.