1.8.3 Нормирование метрологических характеристик си. Класс точности.

Любое Си имеет определенную погрешность, значение которой не должно превышать некоторого предельного значения. В противном случае СИ считают непригодным для применения. Предел допускаемой погрешности – это наибольшая (без учета знака) погрешности СИ, при которой оно может быть признано годным к применению.

Отдельно могут нормироваться основные, дополнительные систематические и случайные погрешности. Наиболее общей характеристикой является класс точности.

Класс точности– обобщенная характеристика СИ, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами СИ, влияющими на точность, значения которых устанавливают в стандартах на отдельные виды СИ.

ГОСТ 8.401-80 «ГСИ. Классы точности СИ. Общие требования» устанавливает общие положения деления СИ по классам точности способы нормирования МХ и обозначения классов точности.

Обозначение класса точностизависит от того, какая из погрешностей нормируется для СИ.

1. Если нормируется предел допускаемой абсолютной погрешности, то классы точности обозначаются латинскими прописными буквами или римскими цифрами, которые непосредственно не отражают значение предельной допускаемой погрешности (в документации указывается: «класс точности – М», на приборе – М).

2. Если нормируются пределы относительной или приведенной погрешности, то классы точности обозначаются арабскими цифрами, которые равны этим пределам в % (если нормируется приведенная погрешность, в документации указывается: «класс точности 0,5», на приборе – 0,5; еслишкала прибора неравномерная, к обозначению класса точности добавляется дополнительный знак:; если нормируетсяотносительная погрешностьв документации указывается: «класс точности», на приборе:).

3. В некоторых случаях, например для цифровых приборов, нормируют относительную погрешность, причем нормирование проводят таким образом, чтобы значение предела зависело от значения измеряемой величины. В этом случае класс точности обозначают двумя числами: с/d(например: 0,1/0,2).CиD– это параметры уравнения для вычисления пределов допускаемой относительной погрешности. Обычно эти уравнения заносят в нормативную документацию на прибор (в его паспорт).

Стандарт (ГОСТ 8.401-80) устанавливает следующий ряд чисел, определяющих пределы погрешностей, а следовательно и классы точности: 1; 1,5; 2; 2,5; 4; 5; 6. Допускается применять: 1,6; 3. Числа ряда могут быть умножены на 10ⁿ, гдеn– целые числа: 1; 0; –1; –2 ….

1.9 Основы теории измерений

1.9.1 Факторы, влияющие на точность измерений.

Все в окружающем нас мире взаимосвязано и взаимообусловлено. Поэтому результат измерения, то есть то, что, мы получаем при проведении измерительной процедуры, определяется не только значением измеряемой величины, но и совместным влиянием целого ряда факторов, учет которых представляет иногда довольно сложную задачу.

Объект измерений.Перед проведением измерения необходимо хорошо изучить объект измерения и представить себе модель исследуемого объекта, которая в дальнейшем, по мере получения измерительной информации, может уточняться. Чем точнее модель соответствует реальному объекту, тем корректнее измерительный эксперимент.

Примеры:

1. При измерении диаметра вала необходимо быть уверенным, что он круглый (иначе неясно какое значение принимать за диаметр). При контроле отклонений формы, наоборот измеряют отклонение от округлости.

2. При измерении периода обращения Земли вокруг Солнца можно пренебречь неравномерностью периода, а можно, наоборот сделать его объектом исследования (измерения).

3. При измерении меняющихся во времени величин часто определяют их средние значения, пренебрегая их измерением. В то же время, существует целое направление – Флуктуационные методы измерений и контроля. Оно основано на изучении флуктуаций (изменений) величины. С помощью этих методов получают необходимую информацию о качестве объекта измерений и осуществляют прогнозирование его технического состояния.

Эксперт или экспериментатор– субъект измерений. Экспериментатор привносит в результат измерения элемент субъективизма, который, по возможности, необходимо стремиться уменьшить. Этот эффект зависит от квалификации измерителя, состояния его здоровья, соблюдения эргономических требований и т.д. Субъективная погрешность измерений исключается путем автоматизации измерений. Если нет возможности перехода к автоматизированным или автоматическим инструментальным измерениям, проводят комплекс мероприятий:

1. к измерениям допускаются лица, прошедшие специальную подготовку, имеющие соответствующие знания, умения, практические навыки;

2. последовательность действий экспериментатора строго регламентируется методикой выполнения измерений.

В

Рисунок 1.1 – Зависимость работоспособности экспериментатора от продолжительности его работы.

ажное значение имеет режим работы экспериментатора, степень его устойчивости. На рисунке 1.1 представлен график зависимости работоспособности экспериментатора в течение рабочей смены.

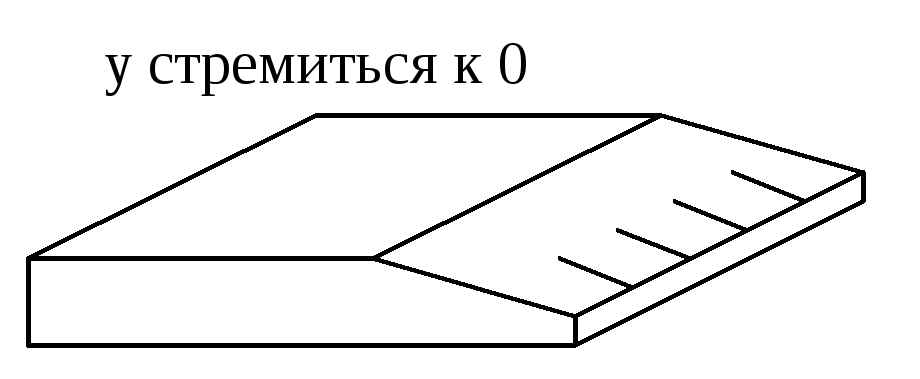
В

Рисунок 1.2:I –указатель; II – шкала.

ажное значение имеют также санитарно-гигиенические условия труда:

Освещенность– мелкие предметы различаются при освещенности 50…70лк. Максимальная острота зрения при освещенности 600…1000лк. При естественном освещении производительность труда примерно на 10% выше, чем при искусственном. Применяют три вида освещения:

• общее – освещение всего помещения (при проведении механических измерений невысокой точности);

• местное – освещение непосредственно рабочего места (при измерении применять не рекомендуется, так как получается неравномерное распределение яркости в поле зрения, что снижает производительность труда, приводит к появлению ошибок, повышает утомляемость).

• комбинированное – сочетание общего и местного освещения (при проведении высокоточных измерений, когда необходимо, чтобы свет на мелкие объекты падал под разными углами).

При оптимальном освещении время ясного видения составляет 3 часа непрерывной работы. Для нормальной работы оператора измерительные приборы располагают в зоне, ограниченной углами 30⁰от оси в горизонтальной и вертикальной плоскостях. Отсчетные устройства располагаются перпендикулярно линии зрения оператора. Относительное расстояние от глаз до шкалы:, гдеh– высота знака; α – угол, равный 40…50⁰.

Н

Рисунок 1.3 – Способы уменьшения погрешности параллакса.

еточность измерения, обусловленная субъективным фактором, называетсясубъективнойилиличнойпогрешностью. Одной из составляющих такого вида погрешности является погрешностьпараллакса, обусловленная отклонением от перпендикулярности, шкалы отсчетного устройства, к линии зрения оператора. Для определения этой составляющей рассмотрим рисунок 1.2.

Применяются различные конструктивные приемы для уменьшения субъективной погрешности параллакса (рисунок 1.3).

Уровень шума– не должен превышать 40..45дБ. Оказывает существенное влияние на результат измерения, на утомляемость и производительность экспериментатора.

Часто для снижения утомляемости применяют функциональную музыку: мелодичные ненавязчивые мелодии со спокойным темпом. Рекомендуемое время звучания музыки – 1,5 …2,5часа за смену.

Метод измерения.Оказывает существенное влияние на результат измерения.

Примеры:1) измерение сопротивления методом амперметра-вольтметра; 2) измерение ЭДС вольтметром; 3) измерение времени (время течет непрерывно, а сигнал поступает дискретно).

Неточность измерений, обусловленная несовершенством метода измерения, называется погрешностью метода или теоретической погрешностью.

Средство измерения. Оказывает двоякое действие на результат измерения. С одной стороны, подключение СИ к объекту измерения может привести и как правило приводит к некоторым изменениям измеряемых величин.

Пример:1) измерение тока амперметром; 2) измерение температуры жидкости ртутным термометром.

С другой стороны, само СИ, в силу ряда причин, допускает неточность при измерении входной величины. К этим причинам можно отнести:

• нелинейность функции преобразования СИ, которая заменяется линейной;

• отклонения действительных значений параметров деталей и элементов СИ от заданных значений;

• износ деталей и элементов СИ;

• зазоры в подвижных соединениях, приводящие к неопределенности во взаимном положении деталей;

• наводки при работе электронных устройств;

• паразитные емкости и индуктивности и т.д.

Неточность измерения, обусловленная используемыми СИ, называют инструментальной погрешностью измерений.

Условия измерения. Это температура окружающей среды, влажность, давление, электромагнитное и гравитационное поля, напряжение в сети, вибрация и т.д.

Очевидно, что все эти факторы влияют на результат измерения, поскольку они приводят к изменениям параметров и размеров деталей и элементов СИ, приводят к возникновению различных помех (изменение сопротивления от температуры – ТКС, изменение линейных размеров от температуры).

Неточность измерений, вызванная условиями измерений, называют погрешностью от изменения условий измерения.