4. Характеристики погрешностей си

Для метрологов наиболее важным является способ выражения погрешности.

По способу выражения различают:

1. абсолютную погрешность – разность между показаниями СИ и значением измеряемой величины

Абсолютная погрешность измеряется в единицах измеряемой величины.

2. относительная погрешность

3. приведенная погрешность

X - нормирующее значение шкалы прибора

Эта погрешность получила название от ее приведения к шкале, она постоянна во всем диапазоне измерений.

Постоянство достигается использованием Х- постоянной зависящей от вида шкалы СИ.

Нормирующее значение – определяется в зависимости от вида шкалы прибора.

1. Если 0 находится на краю или вне диапазона измерений, нормирующее значение равно верхнему пределу измерений.

2. Если 0 находится внутри диапазона измерений нормирующее значение равно наибольшему из модулей пределу измерений.

3. Для электроизмерительных приборов нормирующее значение равно сумме модулей пределов измерений.

4. Для шкалы с условным нулем нормирующее значение равно модулю разности приделов измерения.

5. Если для средства измерения (СИ) нормируется номинальное значение величины, нормирующее значение равно этому номинальному значению.

Эти способы распространяются на равномерные и равностепенные шкалы. В случаи неравномерных шкал нормирующее значение устанавливается равным длине шкалы в мм. Для этих шкал абсолютную погрешность выражают в мм. По условиям окружающей среды различают: 1. Основную погрешность – погрешность СИ при его использовании в нормальных условиях

2. Дополнительная погрешность – погрешность СИ возникающая при отклонении одного из внешних условий от нормальных. В зависимости от режима работы СИ различают: 1. Статическую погрешность – погрешность СИ при измерении установившегося во времени значение величины. 2. Динамическую погрешность – разность между погрешностью СИ в динамическом режиме и его статической погрешностью.

6 Нормирование метрологических характеристик средств измерений. Сущность и назначение процедуры нормирования метрологических характеристик. Понятие «класс точности». Способы обозначения классов точности. Примеры.

Нормирование метрологической характеристики средства измерения (МХСИ). Класс точности?

Любое средство измерение имеет погрешность, значение которого не должно превышать придела допускаемой погрешности. Допускаемая погрешность – это наибольшая по модулю погрешность СИ, при которой оно может быть допущено к применению.

Каждый прибор имеет индивидуальное значение погрешности. Определение погрешности для каждого конкретного прибора была бы очень дорогостоящим и трудоемкой задачей. Чтобы эту задачу устранить вводят комплексную метрологическую характеристику класса точности. Класс точности (КТ) – это обобщенная характеристика СИ, определяющаяся пределами основных и дополнительных погрешностей, а также другими свойствами СИ влияющими на их точность.

Общие требования к КТ устанавливает ГОСТ 8.401- 80 «ГСИ. КТ. СИ. Общие требования». Обозначение класса точности зависит от вида нормируемой погрешности:

1. Если нормируется придел допустимой абсолютной погрешности, то КТ обозначают латинскими прописными буквами или римскими цифрами. Это обозначение не несет в себе информации о значении абсолютной погрешности.

2. Если нормируется придел приведенной погрешности, то КТ обозначается арабскими числами. Число равно приделу приведенной погрешности в %. Оно означает, что для данного СИ нигде в приделах диапазона измерений приведенная погрешность не должна превышать указанного значения.

3. Если нормируется придел допускаемой относительной погрешности, то КТ обозначают арабскими числами в кружочке.

4. В некоторых случаях относительную погрешность нормируется так, чтобы ее предел зависел от значения измеряемой величины. В этом случаи КТ обозначают двумя числами (C/d; 0,1/0,2). Числа C и d – это коэффициенты уравнения, по которому вычисляют придел относительной погрешности.

5. Если шкала прибора не равномерная, то в обозначении КТ добавляют особый знак «галочка» ().

Значение КТ выбирают из ряда предпочтительных чисел: [1,0; 1; 1,5; (1,6); 2,0; 2,5; (3,0); 4,0; 5,0; 6,0]* 10, гдеn= 1; 0; -1; -2; -3;….; -. Числа 1,6 и 3,0 сохранились только для устаревших приборов и в новые не закладываются.

Основы теории измерений.

Факторы, влияющие на точность измерений?

Измерение – это комплексная деятельность, поэтому их точность определяют несколькими группами факторов. Для обеспечения требуемой точности все эти факторы нужно учитывать.

1. Объект измерений. Перед измерением объект изучают и составляют его модель тем, чем точнее модель, тем достовернее будет результат.

2. Эксперт или экспериментатор – субъект измерений. Любой человек вносит в измерение погрешность. Она вызывается опытом человека, остротой его органов чувств, усталостью, а также соответствию отсчетных уставов органам чувств человека.

Одно из составляющих субъективной погрешности измерения является погрешность Параллакса, вызываемая отклонением от перпендикулярности шкалы прибора линии человека.

Для уменьшения погрешности Параллакса используют несколько конструктивных приемов, все они направлены на уменьшение либо угла либо у

А) зеркальная шкала,

Б) фигурные стрелки,

В) фаска,

Г) солнечный зайчик.

3. Метод измерения. - в зависимости от выбранного метода измерений погрешность измерений может быть различной. Эту погрешность называют методической погрешностью.

4. Средство измерений – оказывает двойное влияние на результат: 1) обладает основной погрешностью; 2) вследствие не правильного применения может вносить погрешность в десятки раз больше основной, эта погрешность называется инструментальной погрешностью.

5. Условие измерений – это температура, давление, влажность и т.д. окружающей среды. Эту погрешность называют дополнительной погрешностью.

Таким образом, поскольку на результат измерений одновременно влияет множество разнородных факторов, предсказать его абсолютно точно не возможно.

7 Основной постулат метрологии. Следствия из основного постулата метрологии, обуславливающие правила математического описания результатов измерений. Оценки результатов измерений. Виды оценок и их свойства.

1. Основной постулат метрологии.

Вследствие действия на результат измерений большого количества факторов ОТЧЕТ по шкале СИ всегда является случайным числом. На основании отчета определяют показания средства измерений Из основного постулата метрологии следует 2 следствия:1.Не одну ФВ нельзя измерить абсолютно точно. 2.Т.к. результаты измерений являются случайными числами их нужно обрабатывать с использованием теории вероятности.

2. Положение теории вероятностей, используемые при обработке

результатов измерений.

При обработке результатов измерений используют непрерывные функции распределения вероятностей. В основном равномерную и нормальную функции. Для получения функции распределения вероятностей по результатам измерений выполняем действия: 1.Отмечают результаты измерений на прямой. 2.Разбивают участок от кна несколько (лучше 7) равных отрезков.3.Подсчитывают число результатов попавших в каждый отрезок 4.Находят чистоту попадания результатов в отрезке:

5.Откладывают виде столбиков. Получают гистограмму.6. Соединяют центры столбиков плавной линией и получают полигон распределений. 7.Сравнивают вид полигона распределения с теоретическими функциями распределения вероятностей и делают заключение о виде функции распределения результатов измерений. Нормальному закону подчиняются результаты измерений, если все факторы действуют на результат в равной степени. Равномерное распределение соответствует результатам измерений формирования, которых наибольшую погрешность вносит один из факторов. Функция распределения вероятностей дает полную информацию о результатах измерений, но ее получение очень трудоемкий процесс. Поэтому входе измерений определяют числовые характеристики законов распределения моменты. Это числа, которые получаются из случайных значений но сами случайными не являются. Различают 2 вида моментов законов распределения: 1.Начальные моменты это числовая характеристика закона распределения определяемая от начала координат. В метрологии используют начальный момент первого порядка математическое ожидание или среднее значение измеряемой величины. Матожидание характеризует среднее значение отсчета. На практике экспериментально определитьM(X) невозможно, поскольку число результатов должно стремиться к а оно всегда конечно. В практических расчетах определяют лишь оценку матожидания. Среднее арифметическое значение измеряемой величины.2.Центральные моменты законов распределения это моменты, которые измеряют от центра закона распределения. В метрологии очень широко используют центральный момент второго порядка дисперсию (среднее квадратическое отклонение).При многократных измерениях определяют лишь оценку среднеквадратического отклоненияХарактеристики нормального закона распределения: 1. 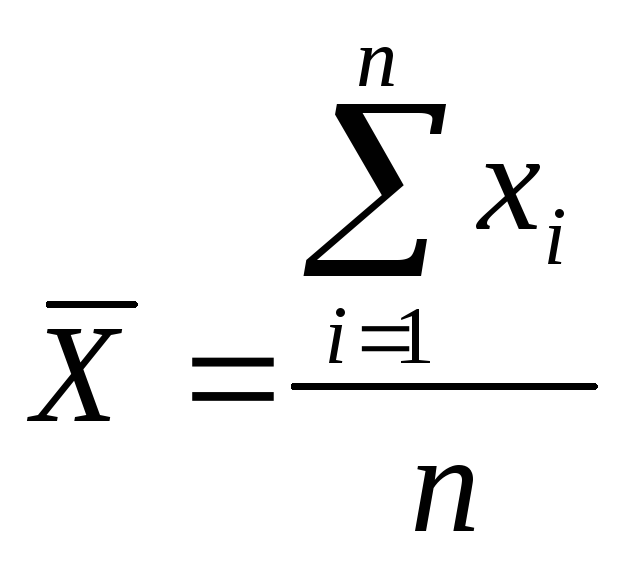Дифференциальная функция распределения .2.Интегральная функция распределения .3.Среднеарифметическое значение .4.Оценка СКО (среднеквадратического отклонения) .5.Значение квантиля распределения зависят от доверительной вероятности. 6.Нормальный закон устойчивый, т.е. комбинация нормальных законов дает тоже нормальный закон. Характеристики равномерного закона распределения: 1.Диффененциальная функция .2.Интегральная функция .3.Среднее значение .4.Оценка СКО .5.Квантиль распределения .6.Равномерный закон не устойчивый. Например, сумма двух равномерно распределенных величин подчиняется закону Симпсона.

Оценки результатов измерений.

После внесения поправок систематическая составляющая погрешности становится нулевой, и погрешность результата измерений можно считать только случайной. Случайная величина должна описываться случайными функциями. Однако для получения моментов случайных функций нужно бесконечное число результатов измерений. На практике это сделать невозможно, поэтому моменты случайных функций определяют приближенно – оценивают. Для этого используют оценки результатов измерений – числа, найденные по результатам измерений и приближенно характеризующие функцию распределения вероятностей результатов измерений.

Например, количество результатов измерений n = 20; мат.ожидание М(х) (≈) ± σ_х (≈S_х) (т.к. число конечно n = 20, то используют приближенные оценки). Оценки результатов измерений могут быть точечными и интервальными.

Точечные оценки – это оценки моментов закона распределения вероятностей результата измерений, которые выражаются одним числом и поэтому изображаются на числовой прямой в виде точки.

К точечным оценкам результатов измерений относятся:

1) Среднее арифметическое значение – это оценка математического ожидания результа измерений, характеризующая его истинное значение

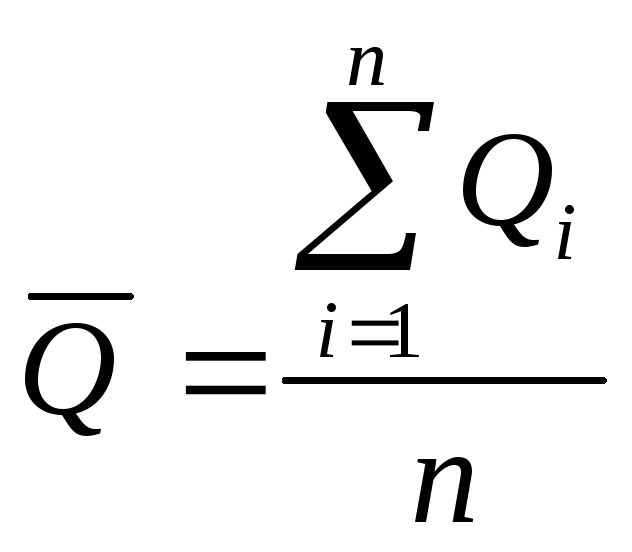
С увеличением числа результатов n точность среднего арифметического значения увеличивается

2) Оценка среднеквадратического отклонения результатов измерений.

Это оценка среднеквадратического значения результатов измерений, которое является мерой рассеивания отдельных результатов измерений около среднего арифметического значения и характеризует погрешность однократного измерения

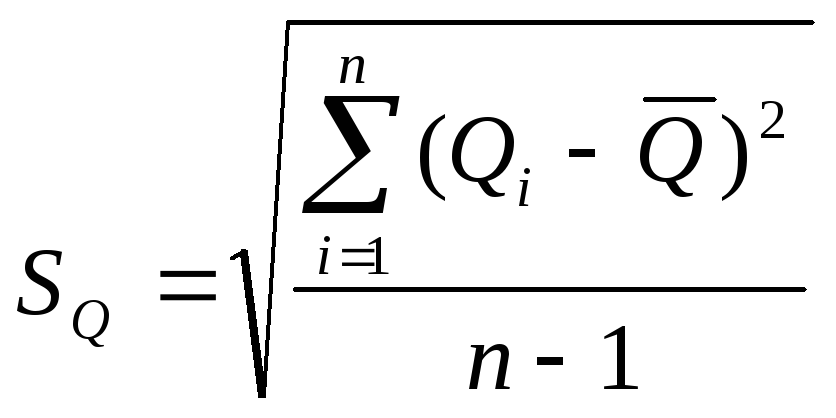
3) Оценка СКО среднего (стандартного) отклонения.

Отклонение – это оценка среднеквадратического отклонения, которое является мерой рассеивания средних арифметических значений около истинного значения измеряемой величины и характеризует погрешность многократного измерения.

Для результатов, подчиняющихся нормальному закону распределения находят по формуле

Интервальные оценки результатов измерения.

С помощью точечных оценок недостаточно наглядно т.к. не дает информации о пределах, в которых лежит истинное значение величины.

Более наглядными являются интервальные оценки. Доверительный интервал и доверительная вероятность.

Доверительный интервал – это интервал значений в котором с принятой доверительной вероятностью лежит истинное значение измеряемой величины E=tS , где t – коэффициент надежности, Е – доверительный интервал.

Для однократного измерения доверительный интервал находится по формуле: E=tS_Q

Зная доверительный интервал можно утверждать, что с принятой доверительной вероятностью Р истинное значение величины лежит в диапазоне Доверительный интервал – это мера точности результата измерений.

Доверительная вероятность – это вероятность с которой определяется доверительный интервал.

Доверительная вероятность – это мера надежности с которой утверждается наличие истинного значения в доверительных границах. Значение доверительной вероятности устанавливает экспериментатор на основании общих рекомендаций к их выбору.

В Машино и Приборостроении для измерения обыкновенной точности используют

Р=0,9…0,95

Для точных измерений

Р=0,99

Для измерений особой точности

Р=0,999

Для оценки качества измерений и качества технологических процессов Р выбирают так, чтобы оно соответствовало «трем сигмам»(сигма – СКО)

Р=0,9927

8 Учет факторов, влияющих на точность результата измерений, на различных этапах выполнения измерений. Виды поправок к результатам измерения, порядок их внесения. Составляющая погрешности, компенсируемая внесением поправок, ее виды. Примеры.