I. Описание критерия q

Для вычисления Q_эмп по данным выборок находят S₁ – количество значений в выборке 1, которые выше максимального значения в выборке 2, и S₂ - количество значений в выборке 2, которые ниже минимального значения в выборке 1.

Q_эмп= S₁+ S₂.

Q_кр находим по таблице критических значений в зависимости от n₁ и n₂.

Далее с помощью оси значимости определяем, какую гипотезу принять, а какую отвергнуть.

зона незначимости зона неопределенности зона значимости

Н_о р≤0,05 р≤0,01 Н₁

Q_крит Q_крит

Графически данный критерий Q можно представить следующим образом:

а) б) в)

Рис.1.

На рис. а) все значения ряда 1 выше значений ряда 2, различия, безусловно, достоверны. На рис. б) диапазоны значений совпадают, различия недостоверны и применение критерия Q бессмысленно. В варианте в) значения рядов частично налагаются друг на друга, поэтому достоверность различий проверяем методом Q, который выясняет, достаточно ли велики значения S₁ и S₂, чтобы утверждать, что различия между выборками статистически значимы. Чем больше Q, тем более достоверные различия сможем констатировать.

Критерий Q – простой непараметрический метод, который позволяет быстро оценить различия между двумя выборками. Но если он не выявляет различий, это не значит, что их действительно нет. В этом случае применяют другие более мощные критерии, такие критерий t-Стьюдента, φ^* Фишера или критерий U Манна-Уитни и др.

Ограничения Q-критерия:

1. В каждой из выборок должно быть не менее 11 испытуемых, при этом n₁ ≈ n₂:

1. если n_1, n₂ ≤ 50, то/ n₁- n₂/≤10;

2. если 51 ≤ n_1, n₂ ≤ 100, то/ n₁- n₂/≤20;

3. n_1, n₂ ≥ 100, то n₁/ n₂ ≈ 1,5 – 2 раза.

2.Диапазоны разброса значений в двух выборках не должны совпадать.

3. При n₁, n₂ > 26 полученное эмпирическое значение сопоставлять с Q_кр=8 (р≤0,05) и Q_кр=10 (р≤0,01).

II. Описание критерия u

Существует несколько способов использования данного метода. Рассмотрим метод, который определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами значений. В отличии от критерия Q этот метод используют, когда ряды «налагаются» частично друг на друга.

Графически данный критерий можно представить следующим образом:

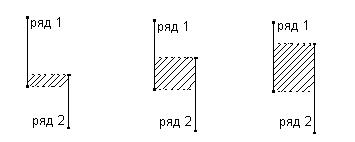
а) б) в)

Рис.2.

На рисунке представлены три из множества возможных вариантов соотношения двух рядов значений. В случае а) область перекрещивания слишком мала, т.е. вероятнее всего различия достоверны. В случае б) область наложения обширна, существуют ли различия, определяется с помощью критерия U. В последнем случае различия скрадываются. Чем меньше область перекрещивающихся значений, тем более вероятно, что различия достоверны. Эмпирическое значение U_эмп отражает то, насколько велика зона совпадения значений, поэтому, чем меньше U_эмп, тем более достоверны различия.

При применении критерия кроме упорядочивания значений признака, необходимо их проранжировать, одновременно оба ряда. Подсчитать сумму рангов отдельно для каждой выборки, сравнить совпадает ли общая сумма рангов с расчетной. И рассчитать U_эмп

U_эмп= n₁ n₂ + - R_x,

где R_x – большая из двух ранговых сумм, а n_х – объем выборки с большей ранговой суммой.

U_кр находим по таблице критических значений в зависимости от n₁ и n₂.

Далее с помощью оси значимости определяем, какую гипотезу принять, а какую отвергнуть. Но так как, чем меньше U_эмп, тем более достоверны различия, зоны на оси значимости поменяются местами. Это критерий – исключение.

зона значимости зона неопределенности зона незначимости

Н₁ р≤0,01 р≤0,05 Н₀

U_крит U_крит

Ограничения критерия:

1. В каждой выборке должно быть не менее 3 наблюдений; допускается в одной 2 наблюдения, но тогда во второй не менее 5.

2. В каждой выборке n₁,n₂≤60 (из-за сложности ранжирования большого количества данных).

Пример. Две группы испытуемых решали задачу. Показателем успешности служило время решения. Одна из групп получала дополнительную мотивацию в виде денежного вознаграждения. Вопрос: влияет ли денежное вознаграждение на успешность решения задачи?

группа без доп. мотвац.	102	104	105	107	108	111	112	113	114	117	122	123			суммы
															1338	111,5
ранги R1	4,5	6,5	8	11,5	14	15,5	17	18	19	24	25	26			189
группа с доп мотвац.	90	95	99	102	104	106	107	107	107	111	115	115	116	116	1490	106,4
ранги R2	1	2	3	4,5	6,5	9	11,5	11,5	11,5	15,5	20,5	20,5	22,5	22,5	162

Из таблицы видно, что время решения задачи у испытуемых с денежной мотивацией меньше, чем в другой группе. Именно на эту выборку приходится меньшая ранговая сумма. Значит, можно сформулировать гипотезы:

H₀ : решение задачи в группе с дополнительной мотивации не успешнее, чем в группе без мотивации.

H₁: решение задачи в группе с дополнительной мотивацией успешнее, чем в группе без мотивации.

n₁=12, n₂=14, N=26.

1. Применим критерий Q Розенбаума.

n₁ ,n₂ >11. / n₁ - n₂ /<10.

S₁=3, S₂=3. Q_эмп=3+3=6.

По таблице критических значений по n₁=12, n₂=14 находим

7 (р≤0,05)

Q_кр=

9 (р≤0,01)

Н_о р≤0,05 р≤0,01 Н₁

6 7 9

По оси значимости делаем вывод, что принимается гипотеза H₀ -решение задачи в группе с дополнительной мотивации не успешнее, чем в группе без мотивации.

2. Применим критерий U.

Проранжируем двав ряда значений.

Общая сумма рангов 189+162=351.

Расчетная сумма Σ R = N(N+1)/2=26(26+1)/2=351.

Тогда

U_эмп=12 14+ - 189=57.

По таблице критических значений по n₁=12, n₂=14 находим

51 (р≤0,05)

U_кр=

38(р≤0,01)

По оси значимости делаем аналогичный вывод, как и в первом случае, что принимается гипотеза H₀ - решение задачи в группе с дополнительной мотивации не успешнее, чем в группе без мотивации.

Н₁ р≤0,01 р≤0,05 Н₀

38 51 57

3. Критерии Н и S предназначены для оценки различий между тремя, четырьмя и т.д. выборками по уровню какого либо признака.

Но если метод Крускала-Уоллиса позволяет установить, что уровень признака изменяется при переходе от группы к группе, но не указывает направление этих изменений, то метод Джонкира выявляет тенденцию изменения признака, что позволяет упорядочить выборки по изучаемому признаку.

Данные выборок для этих критериев должны быть представлены в порядковой, интервальной или шкале отношений и упорядочены по возрастанию.

Гипотезы: H₀ – между выборками 1, 2, 3 и т.д. существуют лишь случайные различия по уровню исследуемого признака.

H₁ – между выборками 1, 2, 3 и т.д. существуют неслучайные различия по уровню исследуемого признака.

В случае S-критерия гипотезы могут формулироваться и другим образом:

H₀ – тенденция возрастания признака при переходе от выборки к выборке является случайной.

H₁ – тенденция возрастания признака при переходе от выборки к выборке не является случайной.