Тема 2.6. Параметрические методы сравнения выборок

План

1. Задачи, решаемые параметрическими методами сравнения.

2. Сравнение средних двух выборок. Критерий t-Стьюдента.

3. Сравнение однородности двух выборок. F-критерий Фишера.

1. Критерии носят название «параметрические», т.к. в формулу их расчета входят такие параметры, как среднее, дисперсия, среднеквадратичное отклонение. С помощью t-критерия можно выявлять различия в уровне исследуемого признака, а также определять достоверность сдвига в его значениях. Кроме этого, критерий t позволяет проверять гипотезу о различии среднего значения одной выборки и некоторой заданной величины.

К параметрическим методам относится и сравнение дисперсий двух выборок по критерию F Фишера. Этот метод приводит к ценным содержательным выводам, а в случае сравнения двух независимых выборок сравнение дисперсий является обязательной процедурой.

Параметрические критерии применимы к выборкам, признак в которых распределен статистически нормально.

Эти критерии хотя и более сложны в вычислениях, но они намного мощнее непараметрических методов.

2. Критерий t Стьюдента предназначен для сравнения двух средних и , которые распределены по нормальному закону. Он имеет широкое применение, т.к. могут сопоставляться связные и несвязные выборки с разными объемами. Выделяют три ситуации сравнения средних:

I. Сравнение несвязных выборок.

Метод позволяет проверить достоверность различий средних значений двух генеральных совокупностей, из которых извлечены две независимые выборки (независимость предполагает не только две группы испытуемых, но и представители двух выборок не составляют коррелирующие пары – дети и родители, мужья и жены и т.д.).

Эмпирическое значение вычисляется по формуле

t_эмп = , где S= , а = – исправленные дисперсии.

Если n₁= n₂=n, то S= /

Если же n₁≠n₂, то

S= .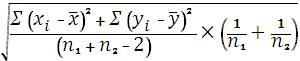

t_кр находится по таблице критических значений в зависимости от числа степеней свободы ν=( - 1) + ( - 1) = _.

P.S. Если распределение признака хотя бы в одной выборке отличается от нормального или дисперсии статистически различаются, то альтернативой данному критерию служит непараметрический критерий U Манна-Уитни.

Пример. Психолог изучал различия в интеллекте студентов 1-го и 5-го курсов по одной и той же методике.

Данные для обработки могут быть занесены в таблицу, позволяющую упорядочить вычисления:

№п/п
	…	…	…	…	…	…
суммы			0		0
средние

После обработки данных, он получил следующие результаты:

=103 при n₁=30 - 1-й курс, =109 при n₂=28 - 5-й курс.

Гипотезы:

Н₀ - интеллект студентов 5-го курса не выше, чем у студентов 1-го курса.

Н₁ - интеллект студентов 5-го курса статистически достоверно выше, чем у студентов 1-го курса

Тогда t_эмп=2,17, ν=30+28-2=56, критические значения находятся приблизительно, т.к. для ν=56

ν	р
	0,05	0,01
40 60	2,02 2,00	2,70 2,66

Эмпирическое значение t_эмп=2,17 находится между критическими значениями для р=0,05 и р=0,01, т.е. р<0,05.

Принимаем гипотезу Н₁ с уровнем значимости 0,05.

II. Сравнение связных выборок.

Метод позволяет определить, достоверны ли различия средних значений двух генеральных совокупностей, из которых извлечены две зависимые выборки (рассматриваются два замера на одной и той же выборке или положительно коррелирующие пары).

Для каждой пары значений находятся разности (сдвиги) d_i=x_i ­- y_i.

Эмпирическое значение t_эмп= , где - среднеарифметическое разностей соответствующих значений = = ,

S= = .

–дисперсия разностей.

Критические значения в таблице в зависимости от ν=n–1.

P.S. Если распределение признака хотя бы в одной выборке отличается от нормального, то альтернативой данному критерию служит непараметрический критерий Т-Вилкоксона.

Пример. При проверке эффективности тренинга каждому из 8 членов группы задавался вопрос «Насколько часто твое мнение совпадает с мнением группы?» до и после тренинга. Ответы давались по 10-балльной шкале: 1–никогда, …,5–в половине случаев,…, 10–всегда. Возрастает ли самооценка конформизма (соглашательство, придерживание мнения большинства) участников в результате тренинга?

Данные занесем в таблицу:

№п/п	Х1	Х2
1 2 3 4 5 6 7 8	3 6 5 2 7 3 4 5	4 6 6 4 6 4 5 6	1 0 1 2 -1 1 1 1	1 0 1 4 1 1 1 1
суммы	35	41	6	10

Гипотезы:

Н₀–увеличение показателя самооценки конформизма после тренинга статистически недостоверно.

Н₁– увеличение показателя самооценки конформизма после тренинга статистически достоверно.

S= ≈0,31, = =0,75, t_эмп= ≈2,42.

По ν=8–1=7 в таблице критических значений находим

2,37 (р≤0,05)

t_кр=

3,50 (р≤0,01)

По оси значимости делаем вывод, что принимается гипотеза H₁ –увеличение показателя самооценки конформизма после тренинга статистически недостоверно с уровнем значимости р 0,05.

Н₀ р≤0,05 р≤0,01 Н₁

2,37 2,42 3,50

III. Сравнение среднего значения одной выборки с известной величиной.

Метод позволяет проверить, достоверно ли, что среднее изучаемого признака отличается от заданной величины А.

Расчет эмпирического значения почти не отличается от случая II: t_эмп= , S= = .

Критические значения в таблице в зависимости от ν=n–1.

Пример. Психолог исследовал влияние условий воспитания в детском доме на интеллектуальное развитие детей. При использование стандартного теста интеллекта для случайной выборки воспитанников детдома были получены следующие результат: =106, s=15, n=36. Вопрос: превышает ли интеллект детей из детдома нормативный показатель А=100.

Гипотезы:

Н₀–средний уровень интеллекта воспитанников детдома не превышает нормативный показатель.

Н₁– средний уровень интеллекта воспитанников детдома превышает нормативный показатель.

t_эмп= 2,4, ν=36–1=35. Критические значения по таблице

ν	р
	0,05	0,01
30 40	2,04 2,02	2,75 2,70

Эмпирическое значение t_эмп=2,4 находится между критическими значениями для р=0,05 и р=0,01, т.е. р<0,05.

Принимаем гипотезу Н₁ с уровнем значимости 0,05.

3. Метод сравнения однородностей позволяет выявить статистически значимые различия между дисперсиями двух генеральных совокупностей, из которых извлечены сравниваемые выборки.

Формула для эмпирического значения критерия F-Фишера:

F_эмп= , причем > , т.е. F_эмп ≥1.

= , аналогично для .

Критические значения находят по таблице в зависимости от ν₁=n₁–1 и ν=n₂–1.

Метод может применяться для проверки предположения о равенстве (гомогенности) дисперсий перед проверкой достоверности различия средних для независимых выборок с разной численностью.

Пример. Детям давались обычные арифметические задачи, и фиксировалось время их решения. После этого одной случайно выбранной половине учащихся сообщалось, что они не прошли испытания, а остальным обратное. Затем у каждого ребенка спрашивали, сколько времени ему понадобилось для решения аналогичной задачи. Сравнивались разности между называемым временем и фактическим. Предполагалось, что сообщение о неудаче вызовет некоторую неадекватность самооценки ребенка.

Были получены следующие данные:

=90.45. =8,16, n₁= n₂=12.

Гипотезы:

Н₀–дисперсия совокупности самооценок не зависит от того, сообщалось детям о неудаче или успехе.

Н₁– дисперсия совокупности самооценок зависит от того, сообщалось детям о неудаче или успехе.

F_эмп= =11,08, ν₁= ν₂=11.

2,82 (р≤0,05)

F_кр=

4,46 (р≤0,01)

По оси значимости делаем вывод, что принимается гипотеза H₁ – дисперсия совокупности самооценок зависит от того, сообщалось детям о неудаче или успехе.

.

Н₀ р≤0,05 р≤0,01 Н₁

2,82 4,46 11,08