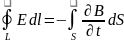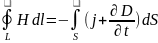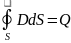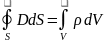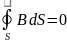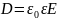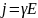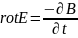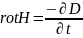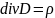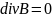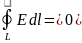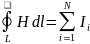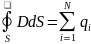- •1. Постоянный электрический ток. Условия существования и т.Д.
- •2. Сторонние силы. Эдс. Напряжение. Закон Ома.
- •3. Закон Джоуля-Ленца в интегральном и дифференциальном виде.
- •Электронная теория электропроводности металлов
- •Электропроводность жидкостей
- •6.Электропроводность газов
- •7. Магнитное поле. Магнитный момент рамки и т.Д.
- •8. Поток вектора магнитной индукции. Теорема Остроградского-Гаусса для магнитного поля.
- •9. Силовое действие магнитного поля и т.Д.
- •10. Закон Био-Савара-Лапласа.
- •11. Применение закон б-с-л для расчёта полей и т.Д.
- •12.Взаимодействие двух параллельных прямых проводников с токами
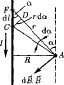
10. Закон Био-Савара-Лапласа.
![]()
Направление dB перпендикулярно dl и r т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть задано по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB если поступательное движение винта соответствует направлению тока в элементе.
Модуль вектора dB определяется выражением
![]() //это dB
//это dB
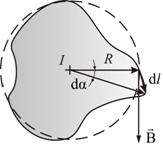
11. Применение закон б-с-л для расчёта полей и т.Д.
Расчет магнитных полей различных проводников с током
Виток с током.
Ра ссмотрим
круговой виток с током, каждый элемент
которого Idl создает
на расстоянии h от
центра витка поле с индукцией dB.
По закону Био-Саварра-Лапласа индукция
равна
ссмотрим
круговой виток с током, каждый элемент
которого Idl создает
на расстоянии h от
центра витка поле с индукцией dB.
По закону Био-Саварра-Лапласа индукция
равна 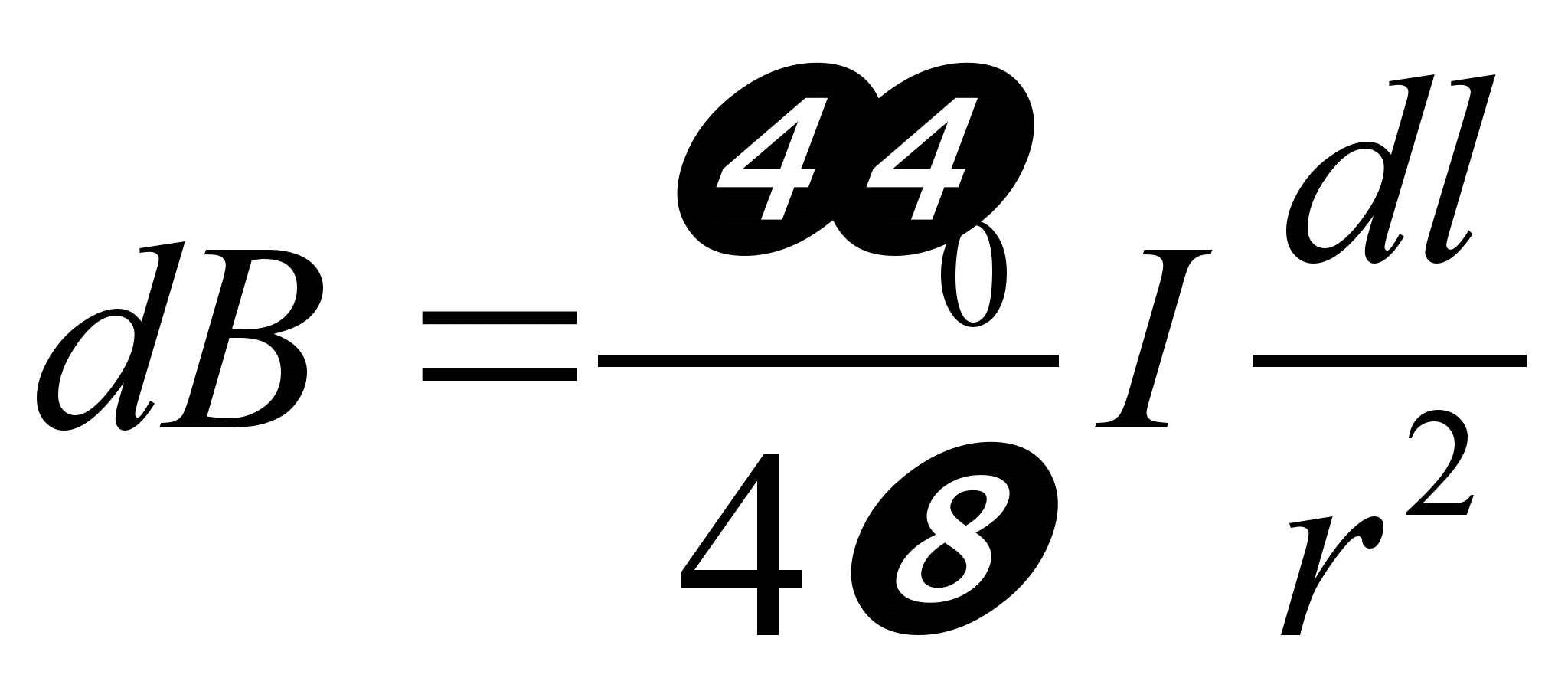 ,
так как элемент контура dl и
радиус-вектор r лежат
во взаимно перпендикулярных плоскостях.
Тогда
,
так как элемент контура dl и
радиус-вектор r лежат
во взаимно перпендикулярных плоскостях.
Тогда ![]() .
В силу осевой симметрии кольца
.
В силу осевой симметрии кольца ![]() ,
значит,
,
значит, 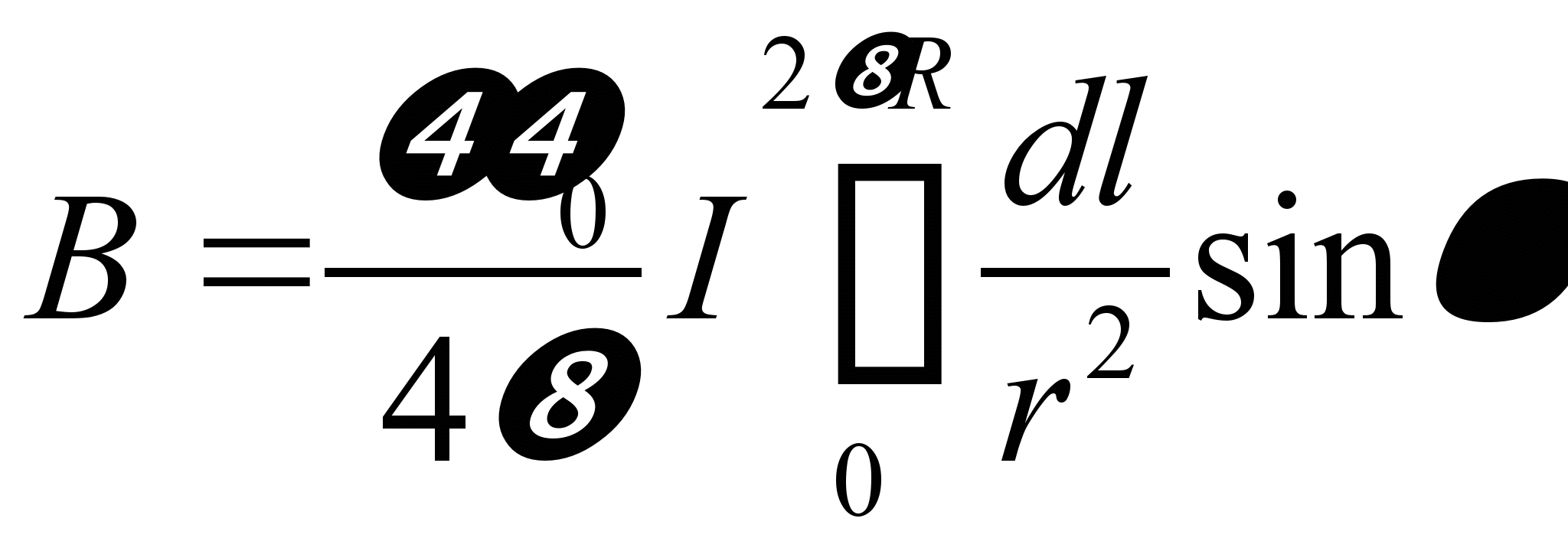 .
Из рисунка видно, что
.
Из рисунка видно, что 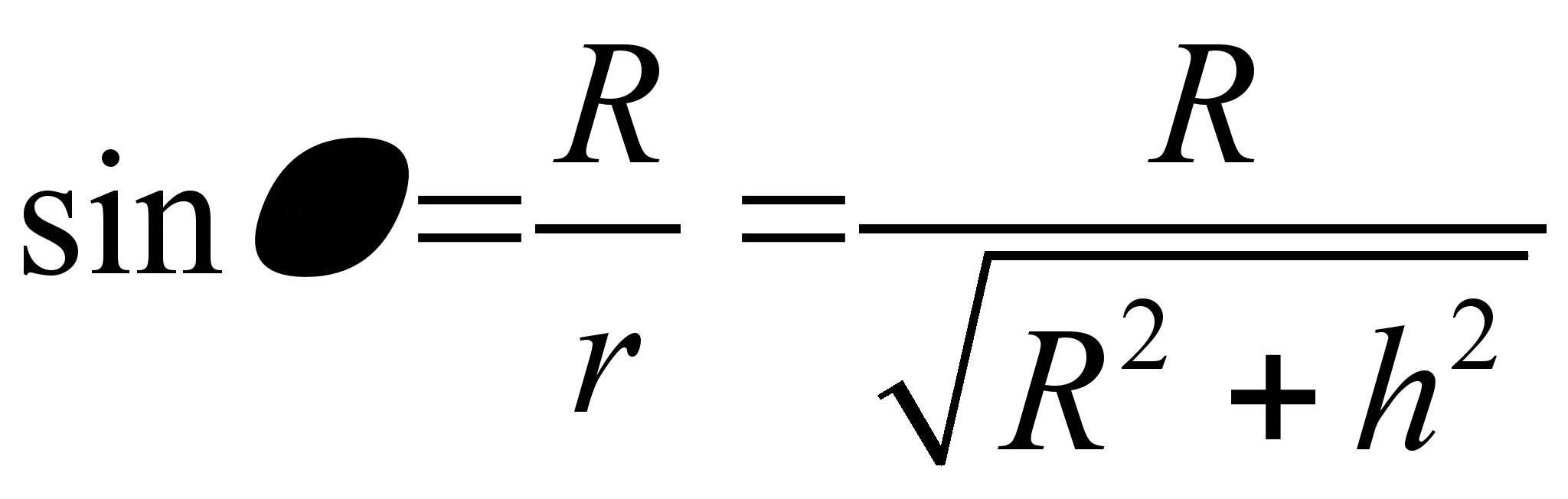 ,
тогда вынося за знак интеграла константы
и интегрируя, получим
,
тогда вынося за знак интеграла константы
и интегрируя, получим 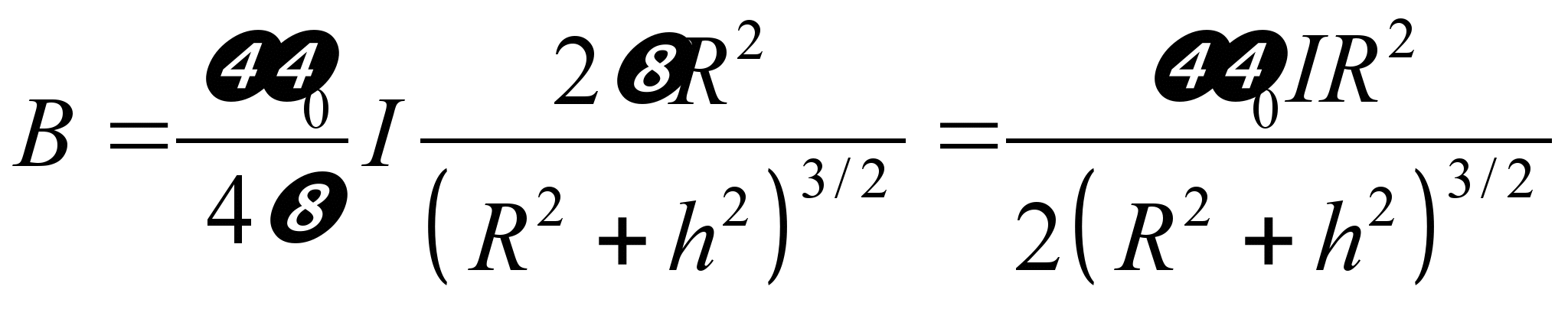 .
Чтобы найти индукцию магнитного поля
в центре витка, положим h =
0 и тогда
.
Чтобы найти индукцию магнитного поля
в центре витка, положим h =
0 и тогда 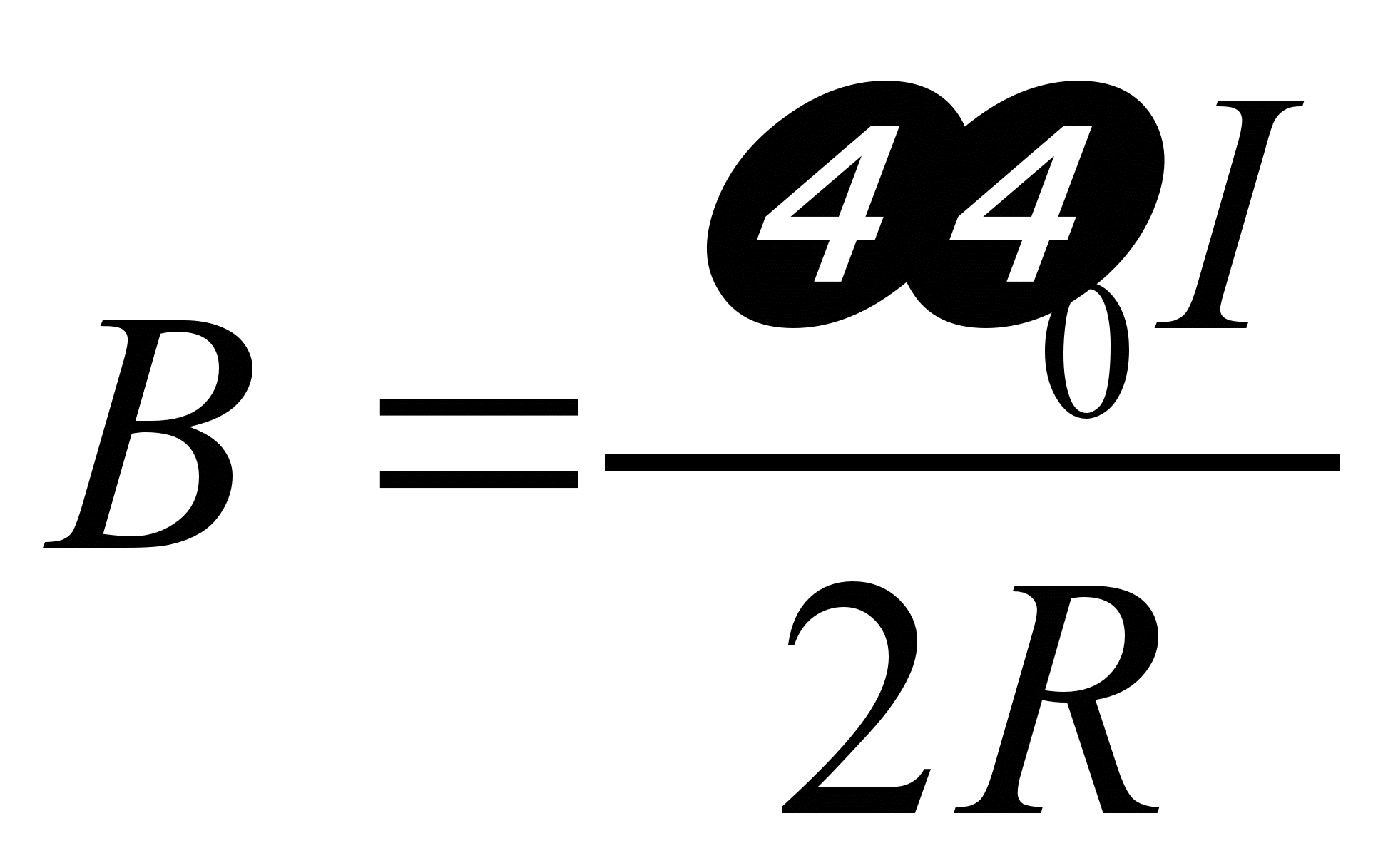
Прямой провод.
Ра ссмотрим
прямой проводник, каждый элемент тока
которого создает поле с индукцией dB.
По закону Био-Саварра-Лапласа индукция
равна
,
тогда
.
В силу осевой симметрии
ссмотрим
прямой проводник, каждый элемент тока
которого создает поле с индукцией dB.
По закону Био-Саварра-Лапласа индукция
равна
,
тогда
.
В силу осевой симметрии ![]() ,
значит,
,
значит, 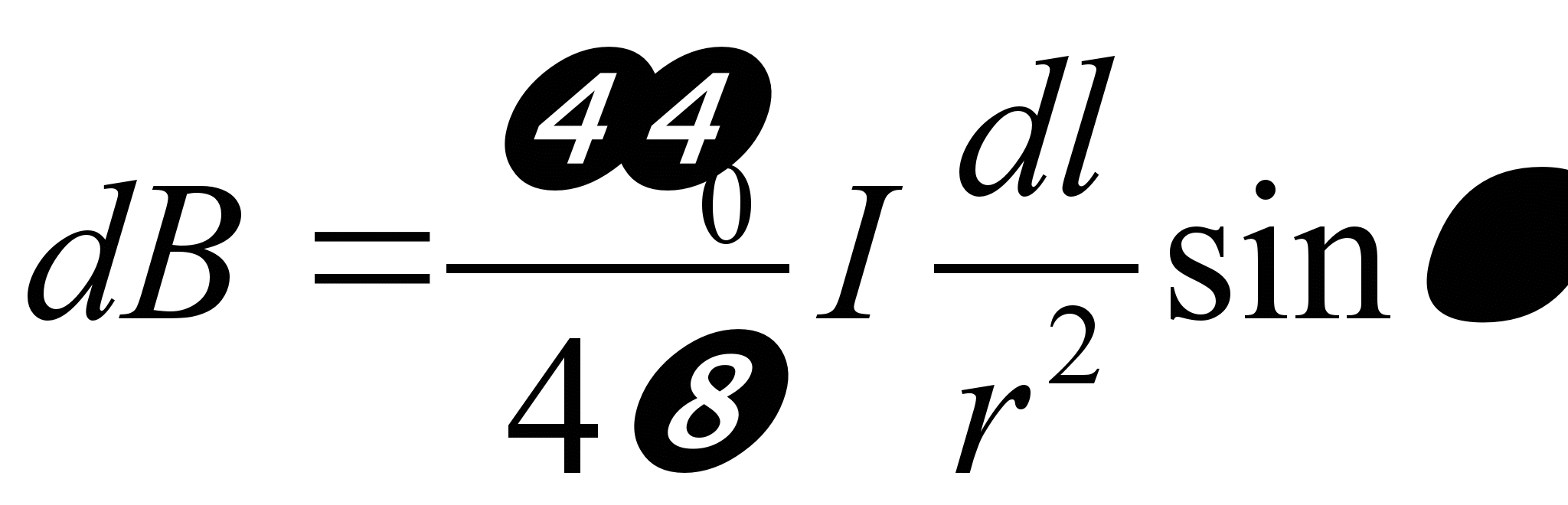 .
Из рисунка видно, что
.
Из рисунка видно, что 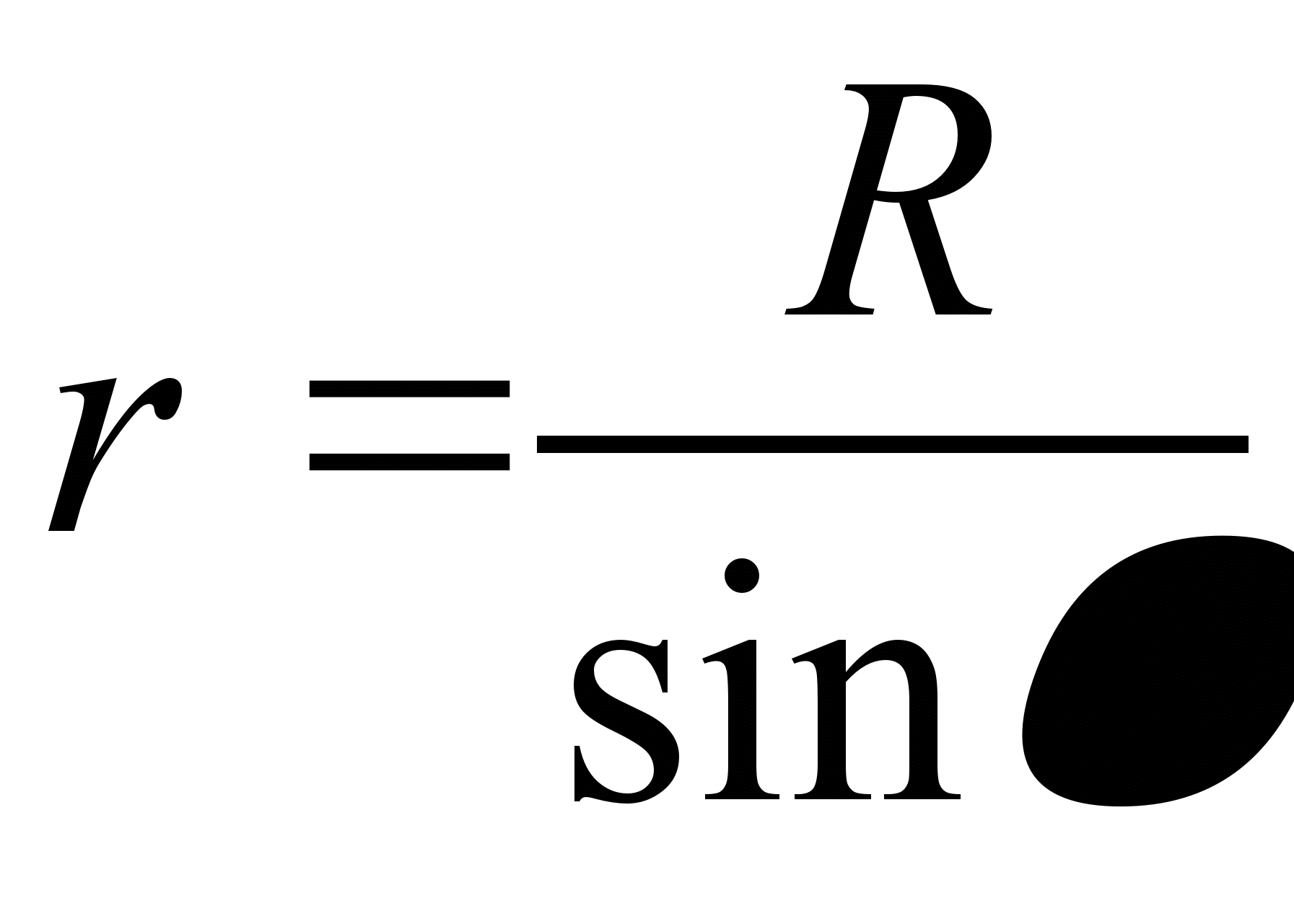 ,
а элемент контура
,
а элемент контура 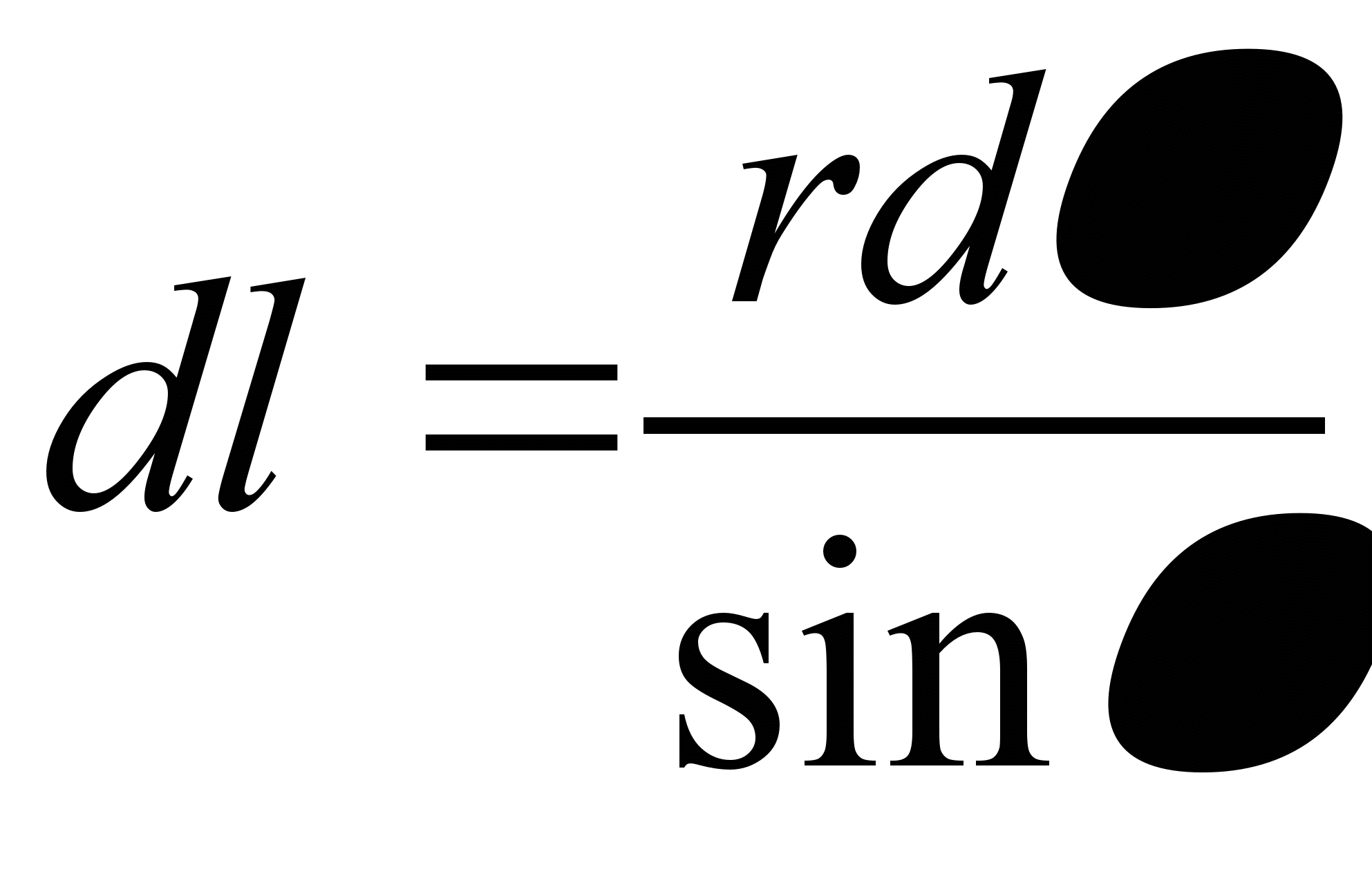 ,
тогда
,
тогда  .
Интегрируя получим
.
Интегрируя получим 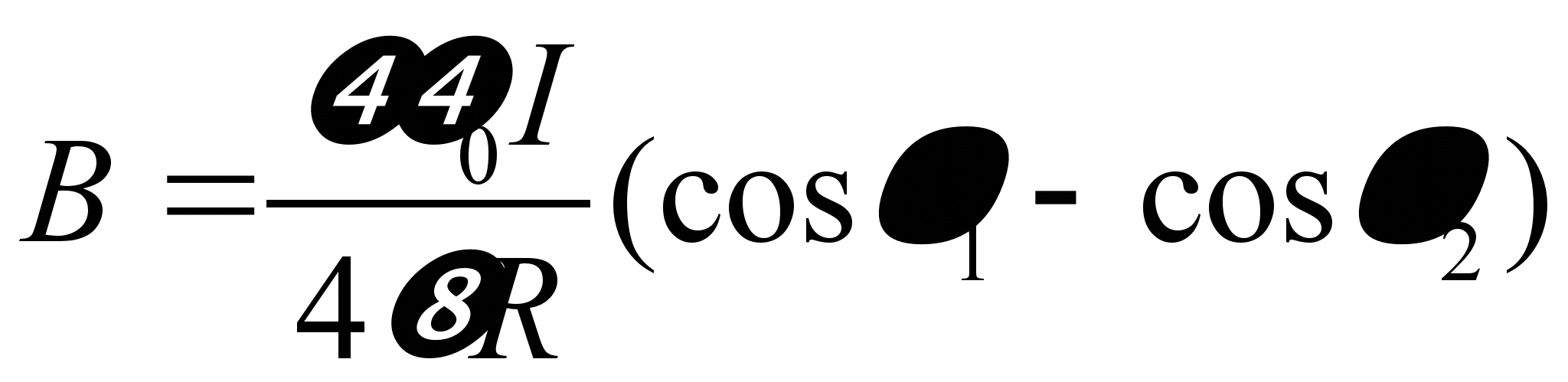 .
Если провод бесконечный, интегрирование
проводится от 1 =
0 до 2 =
,
тогда
.
Если провод бесконечный, интегрирование
проводится от 1 =
0 до 2 =
,
тогда 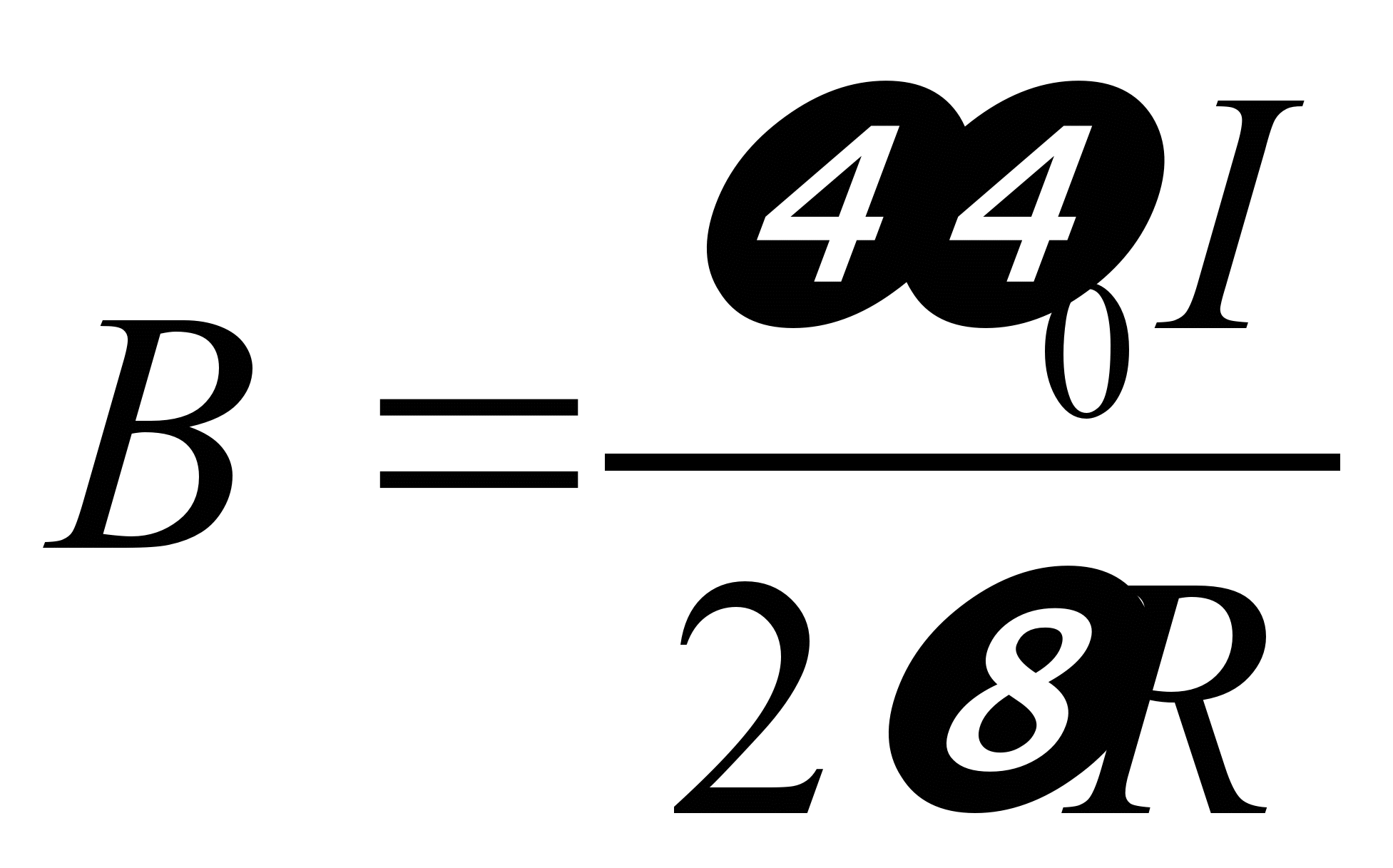
12.Взаимодействие двух параллельных прямых проводников с токами
Два параллельных бесконечно длинных и тонких проводника с токами I1 и I2, расположенные на расстоянии а друг от друга, взаимодействуют с силой на единицу длины
Два параллельных бесконечно длинных и тонких проводника с токами I1 и I2, расположенные на расстоянии а друг от друга, взаимодействуют с силой на единицу длины
![]()
Это вытекает из закона Ампера. Причем, когда токи в проводниках параллельны, проводники притягиваются, а когда токи в проводниках антипараллельны - проводники отталкиваются.
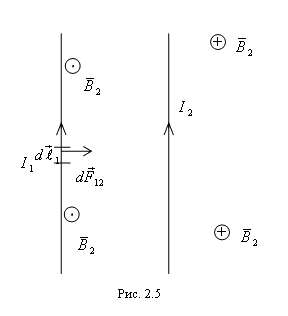 Рис.
2.5
Рис.
2.5
Рассмотрим задачу (рис. 2.5). Первый проводник находится во внешнем поле, созданном вторым проводником. Тогда
![]()
или
![]() .
.
Направления ![]() и
и ![]() взаимно
перпендикулярны и
взаимно
перпендикулярны и
![]() ,
,
и, окончательно:
![]()
или
![]() .
.
Пусть теперь второй проводник находится в поле, созданном первым проводником. Рассуждая по такой же схеме, получим:
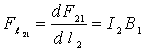
или
![]() ,
,
![]() .
.
13.Циркуляция вектора магнитной индукции |
|
|
|
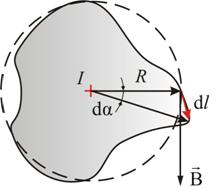
Возьмем
контур l (рис.
2.8), охватывающий прямой ток I,
и вычислим для него циркуляцию вектора
магнитной индукции
Рис. 2.8 Вначале рассмотрим случай, когда контур лежит в плоскости перпендикулярно потоку (ток I направлен за чертеж). В каждой точке контура вектор направлен по касательной к окружности, проходящей через эту точку (линии прямого тока – окружности). Воспользуемся свойствами скалярного произведения векторов.
Отсюда
это теорема о циркуляции вектора : циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную. Иначе обстоит дело, если ток не охватывается контуром (рис. 2.9).
При
обходе радиальная прямая поворачивается
сначала в одном направлении (1–2), а
потом в другом (2–1). Поэтому
Рис. 2.9
Итак,
Эта формула справедлива и для тока произвольной формы, и для контура произвольной формы. Если контур охватывает несколько токов, то
т.е. циркуляция вектора равна алгебраической сумме токов, охваченных контуром произвольной формы.
Теорема
о циркуляции вектора индукции магнитного
поля
Рис. 2.10
Итак,
циркуляция вектора магнитной
индукции
отлична
от нуля, если контур охватывает ток
(сравните с циркуляцией вектора Такие поля, называются вихревыми или соленоидальными.
Магнитному
полю нельзя приписывать потенциал,
как электрическому полю. Этот потенциал
не был бы однозначным: после каждого
обхода по контуру он получал бы
приращение Линии напряженности электрического поля начинаются и заканчиваются на зарядах. А магнитных зарядов в природе нет. Опыт показывает, что линии всегда замкнуты (см. рис. 1.2. и 1.7). Поэтому теорема Гаусса для вектора магнитной индукции записывается так:
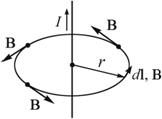
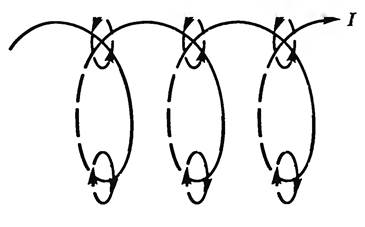
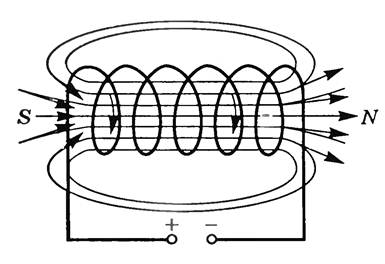
14. Магнитное поле соленоида. Магнитное поле соленоида представляет собой суперпозицию отдельных полей, которые создаются каждым витком в отдельности. Через все витки протекает один и тот же ток. Оси всех витков лежат на одной лини. Соленоид представляет собой катушку индуктивности, имеющую цилиндрическую форму. Эта катушка намотана из проводящей проволоки. При этом витки уложены плотно друг к другу и имеют одном направление. При этом считается, что длинна катушки значительно превышает диаметр витков. Давайте рассмотрим магнитную индукцию, создаваемую каждым витком. Видно, что индукция внутри каждого витка направлена в одну и ту же сторону. Если смотреть в центр витка, то индукция от его краев будет складываться. При этом индукция магнитного поля между двух соседних витков направлена встречно. Так как она создана одним и тем же током то она компенсируется.
Рисунок 1 — Поле создаваемое отдельными витками соленоида
Если витки соленоида намотаны достаточно плотно, то между всеми витками встречное поле будет компенсировано, а внутри витков произойдет сложение отдельных поле в одно общее. Линии этого поля будут проходить внутри соленоида, и охватывать его снаружи. Если исследовать магнитное поле внутри соленоида любыми способами, например, с помощью железных опилок то можно сделать вывод, что оно однородно. Лини магнитного поля в этой области представляют собой параллельные прямые. Мало того что они параллельны сами себе но они еще параллельны оси соленоида. Выходя за приделы соленоида, они искривляются и замыкаются снаружи катушки.
Рисунок 2 — Поле создаваемое соленоидом
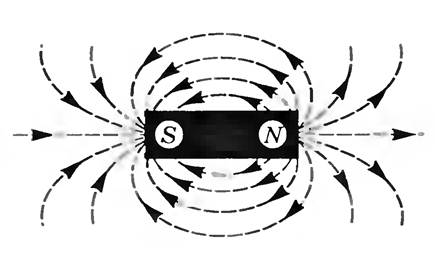
Из рисунка видно, что поле создаваемое соленоидом похоже на поле, которое создает постоянный стержневой магнит. На одном конце силовые линии выходят из соленоида и этот конец аналогичен северному полюсу постоянного магнита. А в другой они входят, и этот конец соответствует южному полюсу. Отличие же заключается в том, что поле присутствует и внутри соленоида. И если провести опыт с железными опилками, то они втянутся в пространство между витками. Но если внутрь соленоида вставить деревянный сердечник либо сердечник из любого другого немагнитного материала, то при проведении опыта с железной стружкой картина поля постоянного магнита и соленоида будет идентична. Так как деревянный сердечник не исказит силовые лини, но при этом не даст проникнуть опилкам внутрь катушки.
Рисунок 3 — Картина поля постоянного стержневого магнита
Для определения полюсов соленоида можно использовать несколько методов. Например, самый простой, использовать магнитную стрелку. Она притянется к противоположному полюсу магнита. Если же известно направление тока в витке полюсы можно определить при помощи правила правого винта. Если вращать головку правого винта в направлении тока, то поступательное движение укажет направление поля в соленоиде. А зная, что поле направлено от северного полюса к южному и можно определить, где какой полюс находится. Чтобы найти модуль магнитной индукции соленоида состоящего из одного слоя можно воспользоваться формулой.
Формула 1 — Модуль магнитной индукции соленоида Где N число витков соленоида l длинна соленоида n число витков на единицу длинны I Ток в соленоиде Мю магнитная проницаемость среды находящейся внутри соленоида Мю0 магнитная постоянная
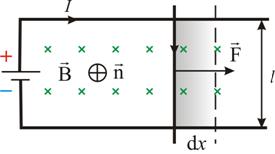
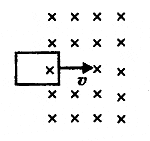
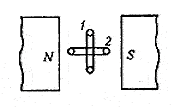
15.Работа совершаемая при перемещении проводника с током и контура в магнитном поле Проводник:
На
проводник с током в магнитном поле
действуют силы, которые определяются
с помощью закона Ампера. Если проводник
не закреплен (например, одна из сторон
контура сделана в виде подвижной
перемычки, рис. 1), то под действием
силы Ампера он в магнитном поле будет
перемещаться. Значит, магнитное поле
совершает работу по перемещению
проводника с током.
Где I- сила тока; l-длина проводника; B-индукция магнитного поля Пусть проводник l переместится параллельно самому себе на расстояние dx. При этом совершится работа:
так
как ldx=dS — площадь, которую пересекает
проводник при его перемещении в
магнитном поле, BdS=dФ — поток вектора
магнитной индукции, который пронизывает
эту площадь. Значит,
Контур: Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле.
Рассмотрим
прямоугольный контур с током 1-2-3-4-1
(рис. 2.18). Магнитное поле направлено
от нас перпендикулярно плоскости
контура. Магнитный поток Ф1 ,
пронизывающий контур, направлен по
нормали
Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и новый контур будет пронизан магнитным потоком Ф2 . Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком Ф* . Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:
где A23 и A41 равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку). A34=I(Ф*+Ф2) .
Провод
1–2 перерезает поток ( Тогда общая работа по перемещению контура A=I(Ф2-Ф1) или A=I∆Ф Где ∆Ф- изменение магнитного потока, сцепленного с контуром Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока, сцепленного с этим контуром. Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле: dA=IdФ 16. Магнитное поле в веществе. Виды магнетиков. Гипотеза Ампера о
молекулярных токах. Вектор
намагничивания.
Различные
вещества в той или иной степени способны
к намагничиванию: то
есть под действием магнитного поля,
в которое их помещают, приобретать
магнитный момент. Одни вещества
намагничиваются сильнее,
другие слабее.
Будем называть все эти
вещества магнетиками.
Для
объяснения способности тел к
намагничиванию, Ампер предположил,
что в молекулах вещества циркулируют
круговые токи (получившие впоследствии
название молекулярных
токов Ампера). Каждый
такой ток обладает собственным магнитным
моментом
Дадим краткую характеристику каждого типа магнетика. Диамагнетики – вещества, характеризуемые отрицательным значением магнитной восприимчивости χ. Вследствие этого вектор намагничивания в этих веществах направлен противоположно внешнему намагничивающему полю . Диамагнетиками являются, например, вода (χ = - 9∙10-6), серебро (χ = - 2,6∙10-5), висмут (χ = - 1,7∙10-4). Парамагнетики – характеризуются положительным значение χ , ведут они себя подобно диэлектрикам с диэлектрической проницаемостью ε>1, то есть вектор в этих веществах параллелен намагничивающему полю . К парамагнетикам относятся алюминий (χ = 2,1∙10-6), платина (χ = 3∙10-4), хлористое железо (χ = 2,5∙10-3). Ферромагнетики – особый вид магнетиков, отличающийся от других магнетиков следующими характерными признаками: 1) высоким значением магнитной восприимчивости (см. таблицу); 2) зависимостью магнитной проницаемости μ от напряженности магнитного поля, вследствие чего зависимость от для этих веществ является нелинейной; 3) наличием петли гистерезиса на кривой намагничивания; 4) существованием температуры, называемой точкой Кюри, выше которой ферромагнетик ведет себя как обычный парамагнетик. Из чистых металлов ферромагнетиками являются железо, никель, кобальт, а также некоторые редкоземельные металлы (например, гадолиний). К числу ферромагнетиков относятся сплавы и соединения этих металлов, а также сплавы и соединения марганца и хрома с неферромагнитными элементами (например, MnAlCu, CrTe и другие). Ферримагнетики (ферриты) – вещества, в которых магнитные моменты атомов кристаллической решетки образуют несколько магнитных подрешеток с магнитными моментами, направленными навстречу друг другу. Имея меньшую величину магнитной восприимчивости по сравнению с ферромагнетиками, в остальном ферримагнетики характеризуются теми же признаками, что и ферромагнетики. Типичными ферритами являются соединения оксидов железа с оксидами других металлов - шпинели (MnFe2O4), гранаты Gd3Fe5O12), гексаферриты (PbFe12O19). Другую группу ферритов образуют двойные фториды типа RbNiF3, а также соединения типа RFe2 (R – редкоземельный металл). Антиферромагнетики – частный случай ферримагнетиков, в которых магнитные моменты подрешеток с противоположно направленными магнитными моментами полностью компенсируют друг друга (скомпенсированный ферримагнетик). Существование антиферромагнетиков было предсказано Л.Д.Ландау в 1933г. В настоящее время известен широкий спектр веществ, обладающих антиферромагнитными свойствами: редкоземельные элементы (Er, Dy, Ho), оксиды и дифториды некоторых металлов (FeO, MnO, CoF2, NiF2), соли угольной и серной кислот (MnCO3, NiSO4) и другие. Сверхдиамагнетики (идеальные диамагнетики) – вещества, магнитная прони-цаемость μ которых равна нулю. Благодаря этой особенности для сверхдиамагнетиков имеет место эффект Мейсснера-Оксенфельда (Meissner W., 1882-1974; Ocksenfeld C.) – полное выталкивание магнитного поля из объема сверхдиамагнетика (магнитная индукция =0). Сверхдиамагнетиками являются все вещества, находящиеся в сверхпроводящем состоянии -низкотемпературные сверхпроводники (металлы) и высокотемпературные сверхпроводники (керамики). Из несверхпроводящих материалов, обладающих сверхдиамагнитными свойствами, известен пока только один пример – хлорид меди (CuCl), открытый в 1986г. (Русаков А.П., МИСиС). 17. Явление электромагнитной индукции. Закон Фарадея. Правило Ленца. ЭДС индукции, возникающая в замкнутом проводящем контуре, численно равна скорости изменяющегося магнитного потока, который пронизывает данное поле. (Определение с лекции)
Явление электромагнитной индукции заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур.
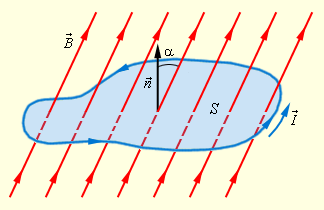
, Рисунок 1. Магнитный поток через замкнутый контур. Направление нормали и выбранное положительное направление обода контура связаны правилом правого буравчика. где B – модуль вектора магнитной индукции, α – угол между вектором и нормалью к плоскости контура
Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура. Единица магнитного потока в системе СИ называется вебером (Вб). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м2:
Фарадей
экспериментально установил, что при
изменении магнитного потока, в
проводящем контуре возникает ЭДС
индукции Закон Фарадея:
Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца. Правило Ленца (Определение с лекции).
При
изменении магнитного потока, который
пронизывает данный проводящий контур,
в этом контуре возникает индукционный
ток такого направления, чтобы его
магнитное поле препятствовало бы
причине, вызвавшей его ток.
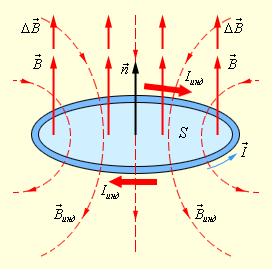
Изменяемое во времени магнитное поле порождает электрическое, которое заставляет заряды двигаться по замкнутому полю (С лекции).
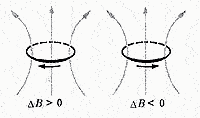
Рисунок
иллюстрирует правило Ленца на примере
неподвижного проводящего контура,
который находится в однородном
магнитном поле, модуль индукции
которого увеличивается во времени.
Иллюстрация
правила Ленца. В этом примере
Правило
Ленца отражает тот экспериментальный
факт, что
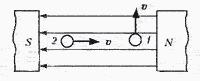
инд и 18. ЭДС индукции в движущихся проводниках. Прямолинейный проводник АВ движется в магнитном поле с индукцией В по проводящим шинам, которые замкнуты на гальванометр.
Готовимся к проверочной работе! 1. При каком направлении движения контура в магнитном поле в контуре будет возникать индукционный ток?
2. Укажите направление индукционного тока в контуре при введении его в однородное магнитное поле.
3. Как изменится магнитный поток в рамке, если рамку повернуть на 90 градусов из положения 1 в положение 2 ?
4. Будет ли возникать индукционный ток в проводниках, если они движутся так, как показано на рисунке?
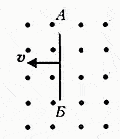
5. Определить направление индукционного тока в проводнике АБ, движущемся в однородном магнитном поле.
6. Указать правильное направление индукционного тока в контурах.
19. Вихревое электрическое поле. Первое уравнение Максвелла. Рассматривая свойства электростатического поля, отмечалось, что работа по перемещению заряда из одной точки поля в другую не зависит от пути. Поле с таким свойством называют потенциальным. Отношение работы по перемещению положительного заряда из бесконечности в какую-либо точку называют потенциалом этой точки, а разность потенциалов двух точек – электрическим напряжением. В электростатическом поле E работа по перемещению единичного заряда по замкнутому контуру L равна нулю (рис. 11.1):
Такой интеграл называют циркуляцией напряженности по замкнутому контуру L. Предел отношения циркуляции векторного поля по замкнутому контуру к площади охватываемого контуром при стремлении ее к нулю называют ротором (rot) векторного поля. Для электростатического поля rot E = 0. Анализируя результаты опытов Фарадея, Максвелл установил, что эдс электромагнитной индукции, возникающая в контуре, пропорциональна скорости изменения магнитного потока, охватываемого этим контуром:
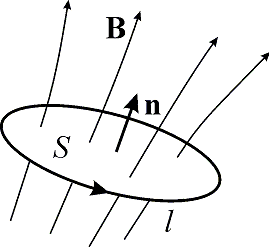
Опыты показали, что эдс индукции не зависит от материала проводника, его состояния и температуры. Максвелл пришел к выводу, что причиной возникновения электромагнитной индукции является само электрическое поле, а проводники играют второстепенную роль и служат только прибором, обнаруживающим это поле. Электроны в проводнике под действием этого поля приходят в движение, и в замкнутой цепи контура возникает индукционный ток. Электрическое поле, возникающее в опытах по электромагнитной индукции, не удовлетворяет условию потенциальности. Особенность этого электрического поля в том, что оно не является электростатическим. Линии напряженности его не начинаются и не заканчиваются на электрических зарядах. Линии напряженности электрического поля, возникающего при электромагнитной индукции, образуют замкнутые кривые. Такое поле называют вихревым электрическим полем. При изменении магнитного поля в какой-либо точке всегда можно найти контур, в котором возникнет эдс индукции, а следовательно, и вихревое электрическое поле. Рассмотрев эти явления, Максвелл пришел к выводу, что всякое изменение магнитного поля вызывает появление электрического поля. Для магнитного потока, пронизывающего контур l, площадью S (рис. 11.1) можно записать соотношение
Рис. 11.1. Контур, охватывающий магнитный поток где Bn – проекция вектора магнитной индукции на ось, параллельную нормали n к элементарной площадке dS. Кроме того, эдс индукции по замкнутому контуру:
Объединяя уравнения (11.1) и (11.3) получим:
Это соотношение выражает связь между вихревым электрическим (E) и переменным магнитным полем (B) и является одним из основных уравнений в теории Максвелла (основной закон электромагнитной индукции).
§ 2. Ток смещения
Рассматривая прохождение переменного электрического тока в цепи, содержащей конденсатор (рис. 11.2) можно заметить, что конденсатор не препятствует прохождению электрического тока, этот ток обеспечивается изменением заряда на обкладках конденсатора. Окружим одну из обкладок конденсатора воображаемой замкнутой поверхностью S. В течение интервала времени dt от источника переменного напряжения по проводнику через эту поверхность переместится заряд dq. По теореме Гаусса поток вектора электрического смещения сквозь замкнутую поверхность равен сумме свободных зарядов, находящихся внутри этой поверхности:
Рис. 11.2. Прохождение переменного электрического тока через конденсатор Изменение потока электрического смещения за время dt равно изменению заряда:
Максвелл назвал величину Iсм током смещения. В соответствии с этим представлением цепь, приведенная на (рис. 11.2), замыкается в конденсаторе током смещения. Найдем плотность тока смещения Iсм на поверхности S:
Максвелл пришел к заключению, что всякое изменение электрического поля вызывает появление магнитного поля, эквивалентного полю, создаваемому токами проводимости. В соответствии с законом полного тока, циркуляция вектора напряженности магнитного поля по замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром. Для плоского конденсатора в области однородного поля , где H – напряженность магнитного поля по длине контура L; Iпр – ток проводимости диэлектрика; jсмS – ток смещения через поверхность S, охватываемую контуром. Для дальнейшего описания теории Максвелла рассмотрим некоторые элементы теории поля.
§ 3. Поля (скалярные и векторные)
Скалярным полем называют пространство, каждой точке которого ставится в соответствие скалярная величина, например температурное поле, распределение плотности, заряда, потенциала и т. д. Скалярные поля удобно отображать в виде поверхностей уровня, на которых поле обладает постоянным значением. Если каждой точке пространства ставится в соответствии вектор, то говорят о векторном поле (например, поле электрической и магнитной напряженности, поле скоростей течения жидкости). Для наглядности представления векторных полей используют линии тока. Это кривые, в каждой точке которых вектор поля есть касательный вектор. Градиентом скалярного поля U называют вектор (обозначаемый gradU), определяемый в каждой точке поля соотношением
где: i, j, k – единичные вектора для осей x, y, z соответственно.
Часто
вектор gradU обозначают
также Градиент потенциала электростатического поля – это напряженность поля:
Если
для векторного поля V(r)
существует функция U(r)
такая, что Дивергенцией (divV) векторного поля V(r) называют скалярную величину
Дивергенция есть мера источников поля. Если, например, в вакууме имеются заряды с плотностью заряда ρ, то напряженность электрического поля E, создаваемая этими зарядами, удовлетворяет уравнению
где ε0 – диэлектрическая постоянная.
Если
Понятие
ротора (rotV)
векторного поля V можно
ввести при помощи понятия циркуляции
векторного поля: В координатном представлении
Для стационарного электрического и магнитного поля:
Кроме того, для всех сред имеются материальные уравнения, которые в случае изотропных, неферромагнитных и несегнетоэлектрических сред имеют самый простой вид.
§ 4. Уравнения Максвелла
Обобщив основные законы электрических и магнитных явлений: теоремы Остроградского-Гаусса, законов полного тока и электромагнитной индукции Максвелл создал теорию, позволяющую решать задачи, связанные с отысканием электрических и магнитных полей, создаваемых заданным распределением зарядов и токов. Согласно этой теории, переменное магнитное поле создает вихревое электрическое, как и переменное, электрическое порождает вихревое магнитное поле. Теория Максвелла представляет собой систему уравнений, в которой свойства среды описываются с помощью трех величин: относительной диэлектрической проницаемости ε, относительной магнитной проницаемости m и удельной электропроводности g. Первое уравнение Максвелла в интегральной форме представляет собой закон электромагнитной индукции:
Если в уравнении (11.11) длина контура L стремится к нулю, то его можно привести к виду:
Это первое уравнение Максвелла в дифференциальной форме. Второе уравнение Максвелла в интегральной форме является законом полного тока:
где Ik – k-й ток, пронизывающий контур L; Iсм – ток смещения. Второе уравнение Максвелла в дифференциальной форме:
Помимо уравнений (11.12) и (11.14) в систему уравнений Максвелла входит теорема Остроградского-Гаусса для электрического и магнитного полей:
Уравнение
(11.16) выражает факт отсутствия свободных
магнитных зарядов. Если ввести объемную
плотность свободных зарядов r и
учесть теорему Гаусса: , (11.17) . (11.18) Полная система уравнений Максвелла:
дополняется материальными уравнениями, связывающими векторы E, D, H и B с величинами, описывающими электрические и магнитные свойства среды:
При заданных начальных условиях система уравнений Максвелла имеет единственное решение. Теория Максвелла не только объяснила уже известные факты, но и предсказала новые явления. Максвелл теоретически предсказал существование электромагнитных волн, распространяющихся в пространстве с конечной скоростью, что в дальнейшем получило блестяще подтверждение.
20. Явление самоиндукции. Ток I, текущий в любом контуре, создает магнитный поток Ф, пронизывающий этот же контур. При изменении I будет изменяться Ф. Следовательно, в контуре будет наводиться ЭДС индукции.
Т.к.
магнитная индукция В пропорциональна
току I
где L – коэффициент пропорциональности, названный индуктивностью контура.
Если
внутри контура нет ферромагнетиков,
то Индуктивность контура L зависит от геометрии контура, числа витков, площади витка контура.
За
единицу индуктивности в СИ принимается
индуктивность такого контура, у
которого при токе Размерность индуктивности:
Вычислим
индуктивность соленоида L.
Если длина соленоида l гораздо
больше его диаметра d (
здесь N –
число витков. Поток через каждый из
витков Потокосцепление
где n –
число витков на единицу длины, т.е.
Из этой формулы можно найти размерность для магнитной постоянной:
При изменении тока в контуре возникает ЭДС самоиндукции, равная:
Знак минус в этой формуле обусловлен правилом Ленца. Явление самоиндукции играет важную роль в электротехнике и радиотехнике. Как мы увидим дальше, благодаря самоиндукции происходит перезарядка конденсатора, соединенного последовательно с катушкой индуктивности, в результате в такой LC-цепочке (колебательном контуре) возникают электромагнитные колебания. 21. Индуктивность соленоида. 22. Энергия магнитного поля. Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:
Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется генри (Гн). Индуктивность контура или катушки равна 1 Гн, если при силе постоянного тока 1 А собственный поток равен 1 Вб:
В качестве примера рассчитаем индуктивность длинного соленоида, имеющего N витков, площадь сечения S и длину l. Магнитное поле соленоида определяется формулой
где I – ток в соленоиде, n = N / e – число витков на единицу длины соленоида. Магнитный поток, пронизывающий все N витков соленоида, равен
Следовательно, индуктивность соленоида равна
где V = Sl – объем соленоида, в котором сосредоточено магнитное поле. Полученный результат не учитывает краевых эффектов, поэтому он приближенно справедлив только для достаточно длинных катушек. Если соленоид заполнен веществом с магнитной проницаемостью μ, то при заданном токе I индукция магнитного поля возрастает по модулю в μ раз; поэтому индуктивность катушки с сердечником также увеличивается в μ раз:
ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно закона Фарадея равна
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней. Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы (рис. 1.21.1). Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Из закона сохранения энергии следует, что вся энергия, запасенная в катушке, выделится в виде джоулева тепла. Если обозначить через R полное сопротивление цепи, то за время Δt выделится количество теплоты ΔQ = I2 R Δt. Ток в цепи равен
Выражение для ΔQ можно записать в виде
В этом выражении ΔI < 0; ток в цепи постепенно убывает от первоначального значения I0 до нуля. Полное количество теплоты, выделившейся в цепи, можно получить, выполнив операцию интегрирования в пределах от I0 до 0. Это дает
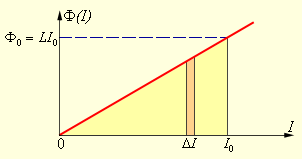
Эту формулу можно получить графическим методом, изобразив на графике зависимость магнитного потока Φ (I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, равное первоначальному запасу энергии магнитного поля, определяется площадью изображенного на рис. 1.21.2 треугольника.
Таким образом, энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, равна
Применим полученное выражение для энергии катушки к длинному соленоиду с магнитным сердечником. Используя приведенные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, можно получить:
где V – объем соленоида. Это выражение показывает, что магнитная энергия локализована не в витках катушки, по которым протекает ток, а рассредоточена по всему объему, в котором создано магнитное поле. Физическая величина
равная энергии магнитного поля в единице объема, называется объемной плотностью магнитной энергии. Дж. Максвелл показал, что выражение для объемной плотности магнитной энергии, выведенное здесь для случая длинного соленоида, справедливо для любых магнитных полей. Энергия магнитного поля (другой способ) Рассмотрим
контур индуктивностью L, по которому
протекает ток I. С этим контуром сцеплен
магнитный поток Ф=LI, поскольку
индуктивность контура неизменна, то
при изменении тока на dI магнитный
поток изменяется на dФ=LdI. Но для
изменения магнитного потока на величину
dФ следует совершить работу dА=IdФ=LIdI.
Тогда работа по созданию магнитного
потока Ф равна
Значит,
энергия магнитного поля, которое
связано с контуром,
23. Гипотеза Максвелла. Второе уравнение Максвелла. Ток смещения. УРАВНЕНИЯ МАКСВЕЛЛА Ограниченность теории дальнодействия. Гипотеза Максвелла. Вихревое электрическое поле. Ток смещения. Система уравнений Максвелла для электромагнитных полей в интегральной форме. Закон неразрывности заряда.
24. Полная система уравнений в инт-ном и диф-ном виде. Электрическое
поле может быть как потенциальным
(EQ),
так и вихревым (EB),
суммарная напряженность равна E
= EQ
+ EB.
Так как циркуляция вектора EQ
равна
нулю (
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и меняющиеся во времени магнитные поля. (См. билет 19) Обобщенная теорема о циркуляции вектора H
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами, либо переменными электрическими полями (См. билет 23) Теорема Гаусса для поля D (электрического)
Если заряд распределён внутри замкнутом поверхности непрерывно с объемной плотностью ρ, то
Теорема Гаусса для поля B (магнитного)
Уравнения, связывающие все эти величины
ε0 - электрическая постоянная μ - магнитная постоянная ε - диэлектрическая проницаемость μ - магнитная проницаемость γ - удельная проводимость вещества
Все эти уравнения и есть полная система уравнений Максвелла в интегральной форме:
В дифференциальной форме:
Если E=const и B=const (стационарный случай), то
Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла — интегральная и дифференциальная — эквивалентны. Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей. Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Уравнения Максвелла — наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т. е. электрическое и магнитное поля неразрывно связаны друг с другом — они образуют единое электромагнитное поле. Одним из важных выводов этой теории явилось существование магнитного поля токов смещения, что позволило Максвеллу предсказать существование электромагнитных волн — переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью. В дальнейшем было доказано, что скорость распространения свободного электромагнитного поля (не связанного с зарядами и токами) в вакууме равна скорости света с = 3108 м/с.
|

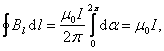 ,
,
 Для
вычисления этой работы рассмотрим
проводник длиной l с током I (он
может свободно двигаться), который
помещен в однородное внешнее магнитное
поле, которое перпендикулярно плоскости
контура. Сила, направление которой
определяется по правилу левой руки,
а значение — по закону Ампера,
рассчитывается по формуле
Для
вычисления этой работы рассмотрим
проводник длиной l с током I (он
может свободно двигаться), который
помещен в однородное внешнее магнитное
поле, которое перпендикулярно плоскости
контура. Сила, направление которой
определяется по правилу левой руки,
а значение — по закону Ампера,
рассчитывается по формуле 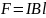
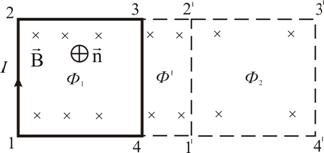
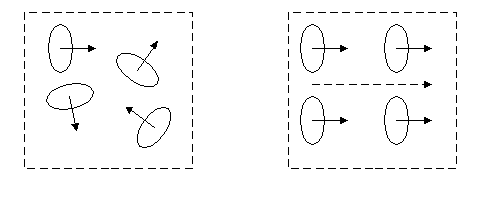 Рис.11.1.
Молекулярные токи Ампера. Намагничивание
вещества.
Под
действием внешнего магнитного поля
магнитные моменты молекул
приобретают преимущественную ориентацию в
одном направлении, вследствие чего
магнетик намагничивается, а его
суммарный магнитный момент становится
отличным от нуля (см. рис.11.1).
Для
характеристики степени намагниченности
вещества используют величину
Рис.11.1.
Молекулярные токи Ампера. Намагничивание
вещества.
Под
действием внешнего магнитного поля
магнитные моменты молекул
приобретают преимущественную ориентацию в
одном направлении, вследствие чего
магнетик намагничивается, а его
суммарный магнитный момент становится
отличным от нуля (см. рис.11.1).
Для
характеристики степени намагниченности
вещества используют величину 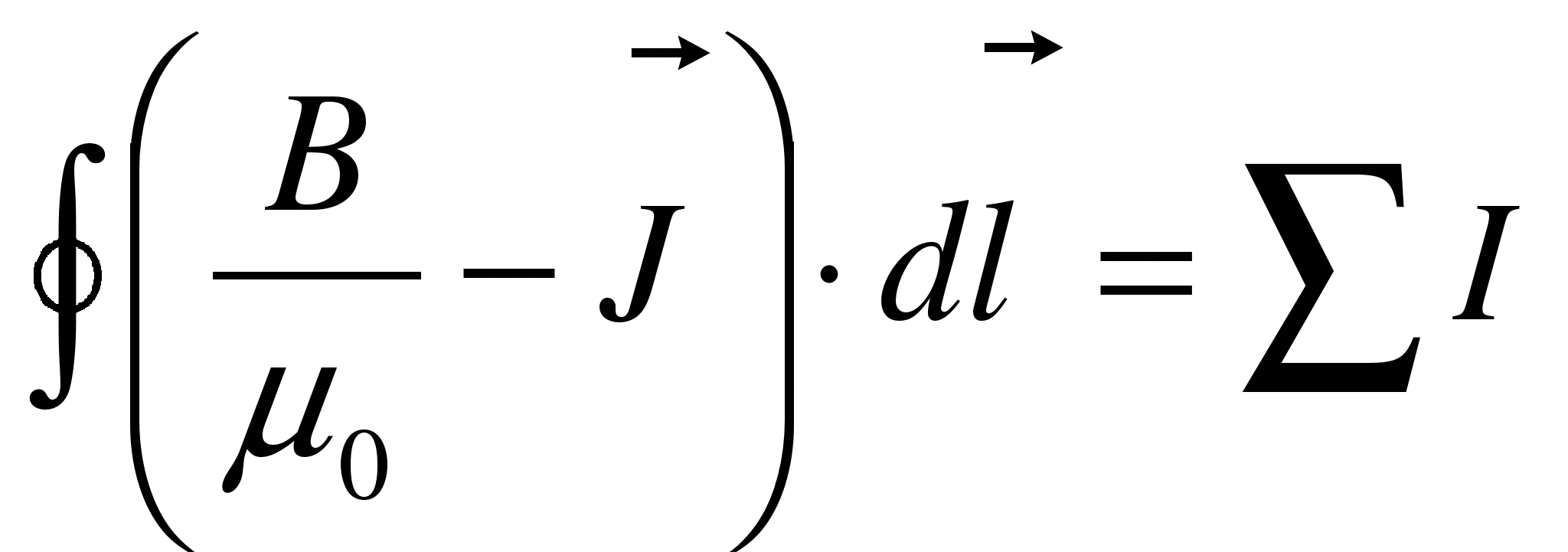 .
Величину,
стоящую в круглых скобках под знаком
интеграла, обозначают буквой
.
Величину,
стоящую в круглых скобках под знаком
интеграла, обозначают буквой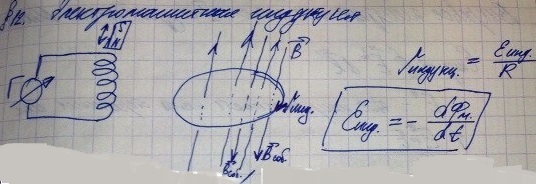
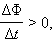 а
инд < 0.
Индукционный ток Iиндтечет
навстречу выбранному положительному
направлению i обхода
контура.
а
инд < 0.
Индукционный ток Iиндтечет
навстречу выбранному положительному
направлению i обхода
контура.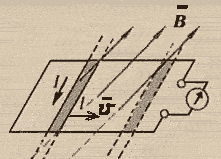 На
электрические заряды, перемещающиеся
вместе с проводником в магнитном поле,
действует
сила
Лоренца:
Fл
= /q/vB sin a
Её направление можно
определить по
правилу левой руки.
Под
действием силы Лоренца внутри проводника
происходит распределение положительных
и отрицательных зарядов вдоль всей
длины проводника l.
Сила Лоренца
является в данном случае сторонней
силой, и в проводнике возникает ЭДС
индукции, а на концах проводника АВ
возникает разность потенциалов.
На
электрические заряды, перемещающиеся
вместе с проводником в магнитном поле,
действует
сила
Лоренца:
Fл
= /q/vB sin a
Её направление можно
определить по
правилу левой руки.
Под
действием силы Лоренца внутри проводника
происходит распределение положительных
и отрицательных зарядов вдоль всей
длины проводника l.
Сила Лоренца
является в данном случае сторонней
силой, и в проводнике возникает ЭДС
индукции, а на концах проводника АВ
возникает разность потенциалов.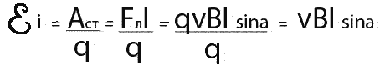 Причина
возникновения ЭДС индукции в движущемся
проводнике объясняется действием
силы Лоренца на свободные заряды.
Причина
возникновения ЭДС индукции в движущемся
проводнике объясняется действием
силы Лоренца на свободные заряды.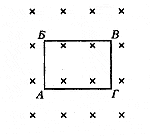
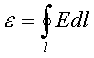 .
(11.3)
.
(11.3)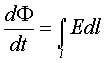 .
(11.4)
.
(11.4)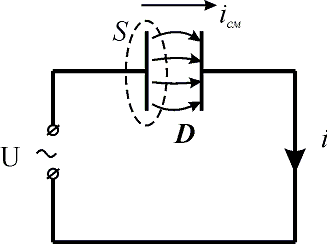
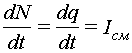 .
(11.6)
.
(11.6)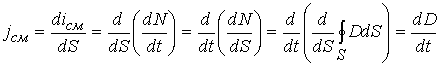 .
(11.7)
.
(11.7)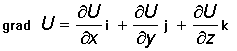 .
.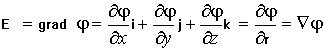 .
(11.8)
.
(11.8)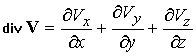 .
.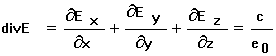 ,
(11.9)
,
(11.9)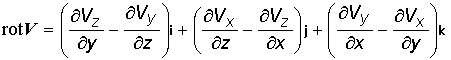 .
.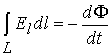 .
(11.11)
.
(11.11)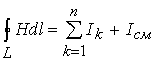 ,
(11.13)
,
(11.13)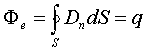 ,
(11.15)
,
(11.15)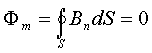 .
(11.16)
.
(11.16)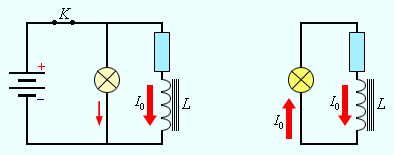
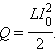
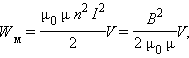
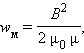
 что
позволяет записать первое
уравнение Максвелла в дифференциальном
виде
что
позволяет записать первое
уравнение Максвелла в дифференциальном
виде
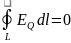 ),
а циркуляция вектора EB
определяется
выражением
),
а циркуляция вектора EB
определяется
выражением
 , то циркуляция
вектора напряженности суммарного
поля
, то циркуляция
вектора напряженности суммарного
поля