7. Магнитное поле. Магнитный момент рамки и т.Д.

·      Сила, действующая на элемент   проводника с током  , помещенного в магнитное поле (сила Ампера),

 

,                                          (21)

где   – вектор магнитной индукции поля.

·      Модуль силы Ампера, действующей на элемент проводника с током,

,                                          (22)

где   – угол между направлением векторов   и  .

·      Полная сила, действующая на весь проводник с током, помещенный в магнитное поле с индукцией  ,

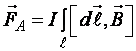.                                          (23)

·      Сила взаимодействия двух проводников с токами   и   (на единицу длины проводника)

,                                             (24)

где   – магнитная постоянная,   – расстояние между проводниками.

 

·      Магнитный момент контура с током

,                                             (25)

где   – магнитный момент;   – сила тока;   – площадь, ограниченная контуром;   – вектор положительной нормали к контуру.

·      Модуль магнитного момента

.                                                (26)

·      Вращающий момент, действующий на контур с током, помещенный в магнитное поле,

,                                            (27)

где  – вращающий момент;   – магнитный момент;   – вектор магнитной индукции поля.

·      Модуль вектора вращающего момента

,                                       (28)

где   – угол между векторами   и  .

·      Сила, действующая на контур с током, помещенный в неоднородное магнитное поле (пондеромоторная сила),

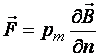,                                             (29)

где   – магнитный момент;   – градиент магнитной индукции поля.

 

·      Модуль пондеромоторной силы

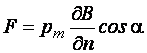,                                      (30)

где   – угол между векторами   и  .

8. Поток вектора магнитной индукции. Теорема Остроградского-Гаусса для магнитного поля.

Потоком вектрора магнитной индукции через площадку dS называется физическая величина, равная скалярному произведению B на dS

где — В cos a — проекция вектора на направление нормали к площадке (а — угол между векторами п dS = = — вектор, модуль которого равен dS, а направление его совпадает с направлением п площадке.

Поток вектора магнитной индукции через произвольную поверхность S равен

Теорема Гаусса для поля поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:

Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

9. Силовое действие магнитного поля и т.Д.

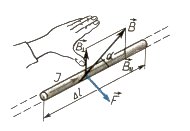
	Сила Ампера. На проводник с током, находящийся в магнитном поле, действует сила, равная F = I·L·B·sin(a), (1) где I - сила тока в проводнике; B - модуль вектора индукции магнитного поля; L - длина проводника, находящегося в магнитном поле; a - угол между вектором магнитного поля и проводником. Сила, действующая на проводник с током в магнитном поле, называют силой Ампера.
Рис. 1.	Направление силы Ампера определяется по правилу левой руки (см. рис.1): четыре пальца по току; перпендикулярная проводнику составляющая вектора индукции В входит в ладонь; отогнутый большой палец дает направление F.
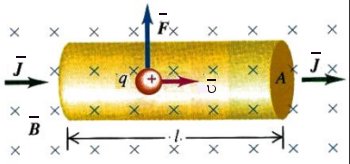
	Сила Лоренца. Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды. Силу, действующую со стороны магнитного поля на движущиеся в нем заряды, называют силой Лоренца. Из закона Ампера (1) следует, что сила Лоренца определяется соотношением: Fл = q·V·B·sin(a). (2) где q - величина движущегося заряда; V - модуль его скорости;  B - модуль вектора индукции магнитного поля; a - угол между вектором скорости заряда и вектором магнитной индукции.
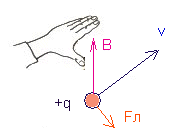
Рис. 2.	Направление вектора Fл определяется по правилу левой руки: четыре пальца по направлению скорости движения положительного заряда V; перпендикулярная скорости составляющая вектора индукции входит в ладонь; отогнутый большой палец дает направление силы Лоренца Fл (см. рис. 2). Примечание: если заряд отрицательный, то направление противоположно тому, которое мы получим по правилу левой руки. Обратите внимание, что Fл перпендикулярна V. Поэтому сила Лоренца не совершает работы, не изменяет модуль скорости заряда и его кинетической энергии. Но направление скорости изменяется непрерывно.
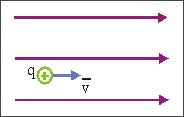
Рис. 3.	Частные случаи 1. Заряд q движется параллельно силовым линиям магнитного поля (см. рис. 3). Т.к. a = 0, то  Fл = 0 и, следовательно, заряд в магнитном поле движется равномерно и прямолинейно.
Рис. 4.	2. Заряд q движется  перпендикулярно силовым линиям магнитного поля (см. рис. 4). Т.к. a = p/2, то Fл = q·v·B. Сила Лоренца создает центростремительное ускорение, равное a = V2/R. Заряд движется по окружности. По второму закону Ньютона не трудно найти радиус окружности и период обращения заряда в магнитном поле: m·v2/R = q·v·B; R = m·V/(q·B); T= 2·p·R/V = 2·p·m/(q·B).