
- •Раздел второй. Экономика Натурального обмена Глава 5. Чистый обмен и основы разделения труда
- •Чистый обмен
- •Общий подход к проблеме
- •Конкретный пример
- •Максимизация полезности в условиях изолированного хозяйствования
- •Эффективность «чистого обмена»
- •Основы разделения труда
- •Общий подход
- •Конкретный пример
- •Оптимальная специализация в условиях фиксированной пропорции обмена
- •Специализация и равновесная пропорция обмена («робинзон-I» продолжает производить часть потребляемого им второго блага)
- •Специализация и равновесная пропорция обмена («робинзон-I» полностью переходит на производство первого блага)
- •Обмен и связанные с ним категории
- •Приложение 1
- •Приложение 2
- •Встречающиеся термины
- •Вопросы и задания
- •Литература
Приложение 1
Модель чистого обмена
Уравнения (1) - (4) представляют модель максимизации величины полезности «робинзона-II» при сохранении уровня благосостояния «робинзона-I» в ходе «чистого обмена». Функция Лагранжа рассматриваемой задачи будет иметь следующий вид:
|
(10) |
Продифференцировав
эту функцию по
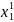 ,
,
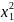 ,
,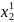 ,
,
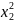 ,
,
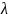 ,
,
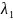 и
и
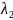 и приравняв полученные результаты нулю,
получим условия первого порядка
максимизации функции
и приравняв полученные результаты нулю,
получим условия первого порядка
максимизации функции
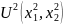 :
:
|
(11) |
|
(12) |
|
(13) |
|
(14) |
|
(15) |
|
(16) |
|
(17) |
Из уравнений (11) - (14) следует:
|
(18) |
Первый и третий члены уравнения (18) представляют собой величины предельных норм замещения первым благом второго блага, соответственно, у «робинзона-I» и «робинзона-II». Их равенство друг другу означает, что исчерпание возможностей обмена, ведущего к максимизации уровня благосостояния «робинзона-II» при сохранении прежней степени удовлетворения потребностей «робинзона-I», происходит по достижении точки пересечения исходной кривой безразличия «робинзона-I» и контрактной кривой.
Приложение 2
Независимость распределения времени между производством обоих благ от изменения трудоемкости производства одного из них в случае, когда функция полезности имеет структуру функции Кобба - Дугласа
Функция
Кобба - Дугласа имеет следующий вид:
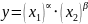 .
Оказывается, что при наделении функции
полезности структурой такой функции
рассматриваемая нами модель изолированного
хозяйствования приобретает следующее
удивительное свойство: в случае изменения
удельной трудоемкости производства
одного из благ оптимальное распределение
времени между их производством остается
прежним. Соответственно, выпуск того
блага, чья удельная трудоемкость не
изменилась, останется таким же, как и
был до этого; выпуск другого блага
изменится пропорционально изменению
трудоемкости его производства. Например,
если трудоемкость производства второго
блага у «робинзона-I»
увеличится вдвое, то оптимальный выпуск
им первого блага никак не изменится, а
второго – сократится в два раза.
.
Оказывается, что при наделении функции
полезности структурой такой функции
рассматриваемая нами модель изолированного
хозяйствования приобретает следующее
удивительное свойство: в случае изменения
удельной трудоемкости производства
одного из благ оптимальное распределение
времени между их производством остается
прежним. Соответственно, выпуск того
блага, чья удельная трудоемкость не
изменилась, останется таким же, как и
был до этого; выпуск другого блага
изменится пропорционально изменению
трудоемкости его производства. Например,
если трудоемкость производства второго
блага у «робинзона-I»
увеличится вдвое, то оптимальный выпуск
им первого блага никак не изменится, а
второго – сократится в два раза.
Приведем доказательство этого утверждения.
Пусть
функция полезности задана формулой
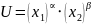 ,
общее время трудовой деятельности
равняется
,
общее время трудовой деятельности
равняется
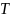 ,
а удельная трудоемкость составляет,
соответственно,
,
а удельная трудоемкость составляет,
соответственно,
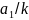 и
,
где
и
,
где
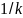 – некоторый произвольный множитель.
Тогда задача состоит в том, чтобы
максимизировать функцию
– некоторый произвольный множитель.
Тогда задача состоит в том, чтобы
максимизировать функцию
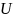 при соблюдении ограничения по времени
производственной деятельности:
при соблюдении ограничения по времени
производственной деятельности:
|
(19) |
при ограничении
|
(20) |
Функция Лагранжа будет иметь следующий вид:
|
(21) |
Соответственно,
частные производные функции Лагранжа
по
 ,
,
 и
,
приравненные к нулю, составят следующую
систему уравнений:
и
,
приравненные к нулю, составят следующую
систему уравнений:
|
(22) |
|
(23) |
|
(24) |
Решение этой системы уравнений дает следующие результаты:
|
(25) |
|
(26) |
Отсюда
видно, что в
условиях изолированного хозяйствования
индивида, функция полезности которого
имеет структуру функции Кобба – Дугласа,
множитель
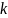 оказывает влияние лишь на величину
.
оказывает влияние лишь на величину
.
Этот вывод распространяется и на случай, когда производитель полностью специализируется на производстве блага, в выпуске которого он обладает сравнительными преимуществами (здесь – второго блага). Отличие заключается лишь в том, что формула (25) определяет количество потребляемого (а не производимого) второго блага, а формула (26), характеризующая количество поступающего через обмен первого блага, должна выглядеть следующим образом:
|
(27) |
где
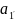 - альтернативные издержки производства
первого блага.
- альтернативные издержки производства
первого блага.

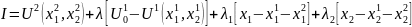

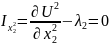
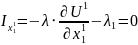
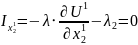
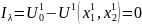
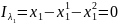
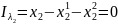
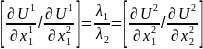
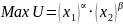
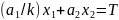
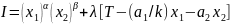

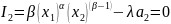
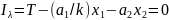

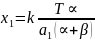
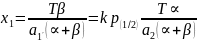 ,
,