Практичне заняття 2 Тема: Похибки обчислення функцій

Мета. Поглибити та уточнити знання, здобуті на лекції та під час самостійної роботи з теоретичним та практичним навчальним матеріалом, сформувати вміння обчислювати похибки функцій.

Вхідний контроль

1. Назвати джерела отримання наближених чисел.

2. Дати означення абсолютної похибки наближення.

3. Сформулювати правило заокруглення чисел.

4. Дати означення відносної похибки наближення.

5. Які цифри числа називаються значущими?

6. Як визначають вірні цифри наближеного числа?

7. Сформулювати правила дій над наближеними числами.

8. Якщо незалежна змінна х відома з деякою точністю, з якою точністю можна знайти значення функції ?

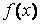9. Якщо необхідно отримати значення функції із заданою точністю, то якою повинна бути точність значення незалежної змінної ?

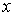10. Як знайти граничну відносну похибку степеневої функції за відомою граничною відносною похибкою аргументу?

11. Як знайти граничну абсолютну похибку логарифмічної функції за відомою граничною відносною похибкою аргументу?

12. Оцінка похибки обчислення функції двох змінних.

13. Оцінка похибки обчислення функції, заданої у неявному вигляді.

Теоретичні відомості

Нехай відомі похибки деякої системи величин. Потрібно визначити похибку даної функції від цих величин.

Нехай задана диференційованана функція

u = f (x₁, x₂, … , x_n)

і нехай │Δx_і│ (і = 1, 2, … , n) абсолютна похибка аргументів функції. Тоді абсолютна похибка функції

Як правило, на практиці │Δx_і│ настільки мала величина, що добутками, квадратами і вищими степенями можна знехтувати. Тому можна покласти

Тут повний приріст замінюємо повним диференціалом, отже

(1)

Позначивши через Δx_і (і = 1, 2, … , n) граничні абсолютні похибки аргументів x_і, а через Δu – граничну похибку функції і для малих Δx_і одержимо

– гранична абсолютна похибка функції (2)

Поділивши обидві частини нерівності (1) на │u│, одержимо оцінку для відносної похибки функції u

Тоді гранична відносна похибка

Наприклад, для двох змінних

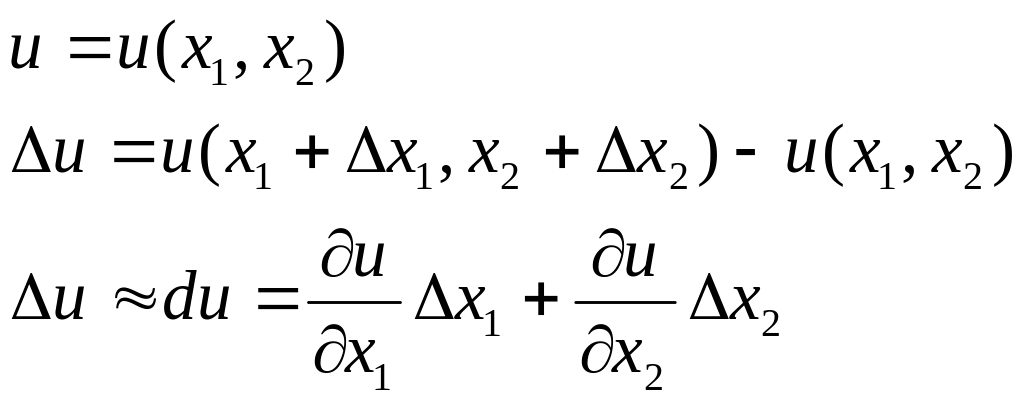
Абсолютну похибку неперервної функції ,що обумовлена достатньо малою похибкою аргументу можна оцінити величиною: . Така оцінка є прийнятною, якщо максимальне значення на інтервалі становить не більше 10% від величини відношення .

Похибка логарифмічних функцій

Абсолютна похибка натурального логарифма будь-якої величини дорівнює відносній похибці цієї величини: .

Абсолютна похибка десяткового логарифма приблизно складає 43% від відносної похибки самої величини: . Отже при обчисленні логарифмів доцільно користуватись такими значеннями, в яких кількість десяткових знаків на одиницю більша ніж задана точність.

Похибка степеневих і показникових функцій

Відносна похибка степеневої функції пропорційна відносній похибці аргументу: .

Відносна похибка показникової функції пропорційна абсолютній похибці аргументу: .

Похибка тригонометричних функцій

Абсолютна та відносна похибки тригонометричних функцій , і оцінюються за наступними формулами:

/

можна зауважити, що абсолютна похибка і не перевищує абсолютної похибки аргументу.

Абсолютна похибка диференційованої функції декількох аргументів

Абсолютна похибка функції обумовлена похибками своїх аргументів:

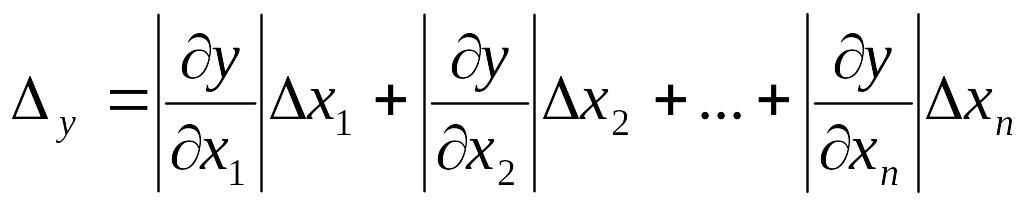
Похибка операції усікання

Похибка усікання виникає коли складний математичний вираз заміщується більш простою формулою. Термін виник з техніки заміни складних функцій вкороченим рядом Тейлора. Елементарні функції можна розкласти у нескінченний ряд, але при обчисленні ми можемо брати лише перші члени ряду.

Приклад.

Для обчислення ми можемо взяти п‘ять перших членів. Так

Похибка округлення

Помилка округлення пов‘язана з обмеженим представленням мантиси десяткового числа. При комп‘ютерних обчисленнях результати арифметичних операцій округлюються і похибка поширюється на наступні обчислення, тому необхідно вибирати такий тип даних для збереження значень, який на декілька розрядів довший ніж задана точність.

Використання наближених і еквівалентних формул

При комп‘ютерних обчисленнях необхідно бути дуже уважними до предсталення формул в тому чи іншому вигляді. Це пов‘язане з такими помилками, як зникнення порядку та ділення на нуль. Також треба пам‘ятати, що в пам’яті комп‘ютера всі дійсні числа представлені наближено і їх неможна безпосередньо порівнювати , лише з перевіряти на рівність з певною степінню точності: .

Для уникнення фатальних помилок при виконані комп‘ютерних обчислень іноді доцільно математичні вирази заміщувати еквівалентними або наближеними формулами, багато з яких беруться із розкладання функцій в ряд але при цьому ні в якому разі не можна нехтувати оцінкою похибки.

Для степеневих функцій застосовують наближену формулу: з похибкою .

Для вилучення кореня степені маємо з похибкою порядку . При діленні – з похибкою .

Така проста задача як обчислення коренів квадратного рівняння при малих значеннях добутку може призводити до помилки зникнення порядку. Тому у таких випадках формулу коренів (3)

Модна замінити еквівалентною формулою помноживши (1) на спряжене

(4)

Зрозуміло, що для випадку краще обчислювати за формулою (4), а – за формулою (3). При , навпаки – за формулою(3), а за формулою (4).

Точний підрахунок похибок результатів обчислень наближених чисел досить громіздкий. Тому здебільшого на практиці точно не враховують похибок, а користуються правилами, підрахунку цифр за В. М. Брадісом:

1. При додаванні і відніманні наближених чисел молодший збережений розряд результату має бути найбільшим серед розрядів, що виражаються останніми значущими цифрами вихідних даних.

2. При множенні і діленні наближених чисел у результаті потрібно зберегти стільки значущих цифр, скільки їх має наближене дане з найменшою кількістю значущих цифр.

3. При піднесенні до квадрата або до куба в результаті треба зберегти стільки значущих цифр, скільки їх має число, яке підносять до степеня.

4. При добуванні кореня в результаті слід брати стільки значущих цифр, скільки їх у підкореневому виразі.

5. При обчисленні проміжних результатів потрібно брати на одну - дві цифри більше, ніж рекомендують попередні правила.

6. Якщо дані можна брати з довільною точністю, то, щоб знайти результат з k правильними цифрами, дані треба брати з такою кількістю цифр, яка забезпечує k + 1 правильну цифру в результаті, відповідно до правил 1-4.

7. При обчисленнях одночленних виразів за допомогою логарифмів слід підрахувати кількість значущих цифр у тому наближеному даному, яке має їх найменше, і взяти таблицю логарифмів з кількістю знаків, на одиницю більшою. У кінцевому результаті остання цифра відкидається.

Примітка. В основу цих правил покладено принцип академіка О. М. Крилева—основний принцип звичайних обчислень, тобто обчислень без строгого врахування похибок: Наближене число слід писати так, щоб у ньому всі цифри, крім останньої, були правильними і лише остання була сумнівною, притому не більш як на одну одиницю.