

Скачано с http://antigtu.ru
Задача Кузнецов Графики 1-7
Условие задачи
Построить графики функций с помощью производной первого порядка.
Решение |
|
antigtu |
|
|
|
||
1) |
Область определения: |
|
|
2) |
Четность функции: |
|
|
Функция общего вида. |
|
|
|
3) |
Интервалы возрастания и убывания: |
|
|
|
Скачано |
с |
|
|
|
|
|
4)График функции: |
|
|
|
. |
ru |
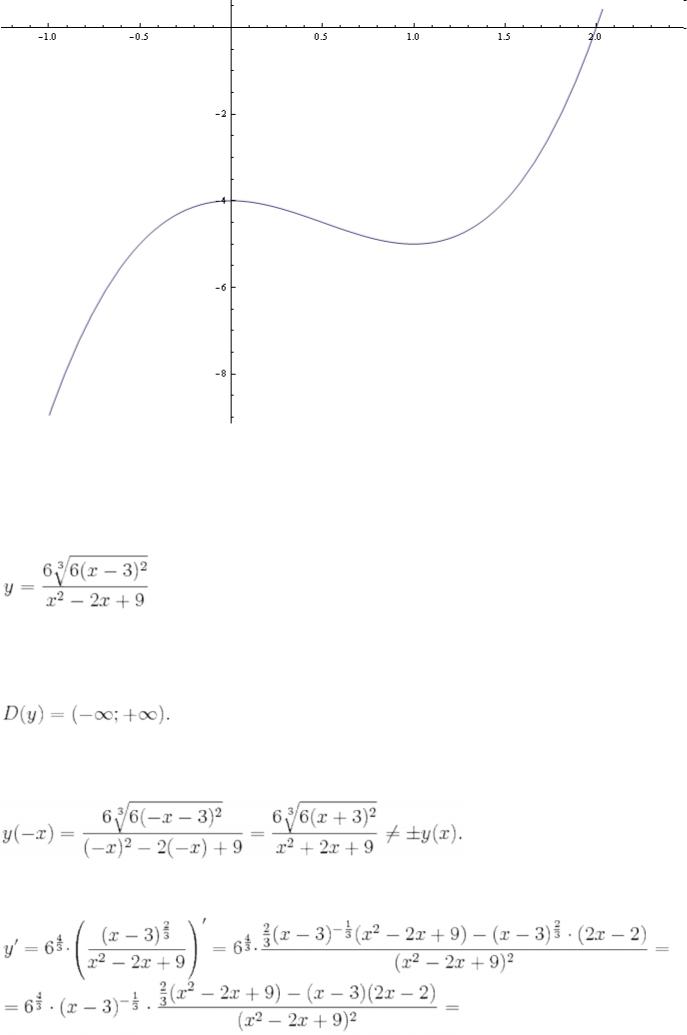
Задача Кузнецов Графики 2-7
Условие задачи
Построить графики функций с помощью производной первого порядка. |
||||
|
|
|
с |
antigtu |
Решение |
|
|
||
|
|
|
||
1) |
Область определения: |
|
|
|
2) |
Четность функции: |
|
|
|
Функция ни четная ни не етная. |
|
|
||
3) |
Интерв лы возр ст ния и убывания: |
|
|
|
|
|
Скачано |
|
|
. |
ru |

При |
- не существует. |
4)График функции: |
с |
|
|
Скачано |
|
Задача Кузнецов Графики 3-7 |
|
Условие задачи
Найти наибольшее и наименьшее значения функций на
antigtu |
. |
ru |
|
|
заданных отрезках.
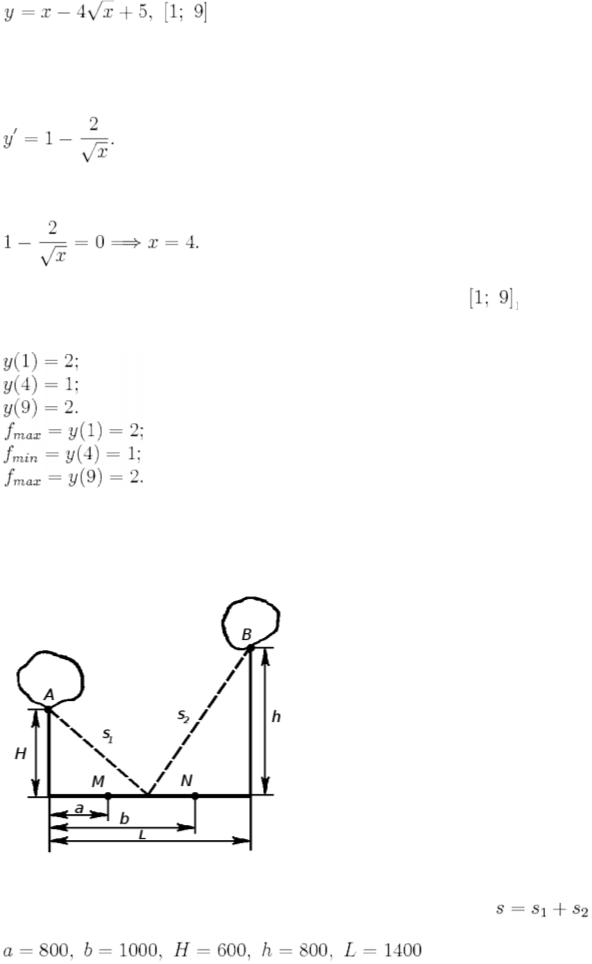
Решение |
|
|
|
. |
ru |
1) Ищем производную заданной функции: |
|
|
|||
2) Находим критические точки функции: |
|
|
|||
Вычислим значения функции в критических точках внутри отрезка |
и значения функции на |
||||
концах отрезка: |
|
antigtu |
|
|
|
Задача Кузнецов Графики 4-7 |
с |
|
|
||
Условие задачи |
|
|
|||
|
|
|
|||
|
|
|
|
|
|
Рыбаку нужно перепр виться с острова A на остров B (см. рис.). Чтобы пополнить свои запасы, он |
|||||
должен попасть на участок берега MN. Найти кратчайший путь рыбака |
|
. |
|||
Решение |
Скачано |
|
|
|
|
|
|
|
|
|
|

Через |
обозначим точку, где рыбак сойдет на берег (точка |
находится между точками |
и ). |
|||||
И пусть |
. Тогда: |
|
|
antigtu |
. |
ru |
|
|
|
|
|
|
|
||||
Откуда общий путь рыбака: |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
Найдем точки экстремума функции |
: |
|
|
|
|
|
|
|
|
Скачано |
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставим заданные зн чения: |
|
|
|
|
|
|
|
|
Вычислим значения функции в критических точках внутри отрезка |
|
и значения |
|
|||||
функции на концах отрезка: |
|
|
|
|
|
|
|
|
