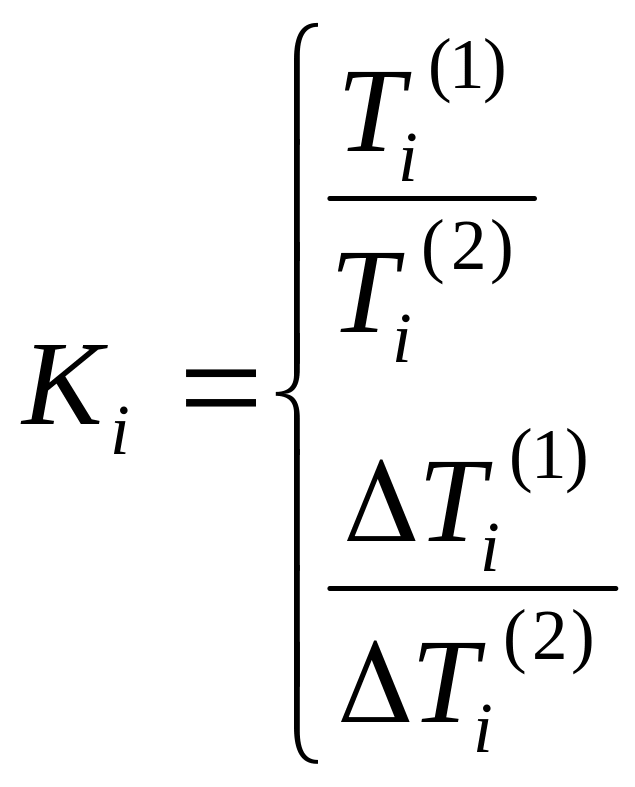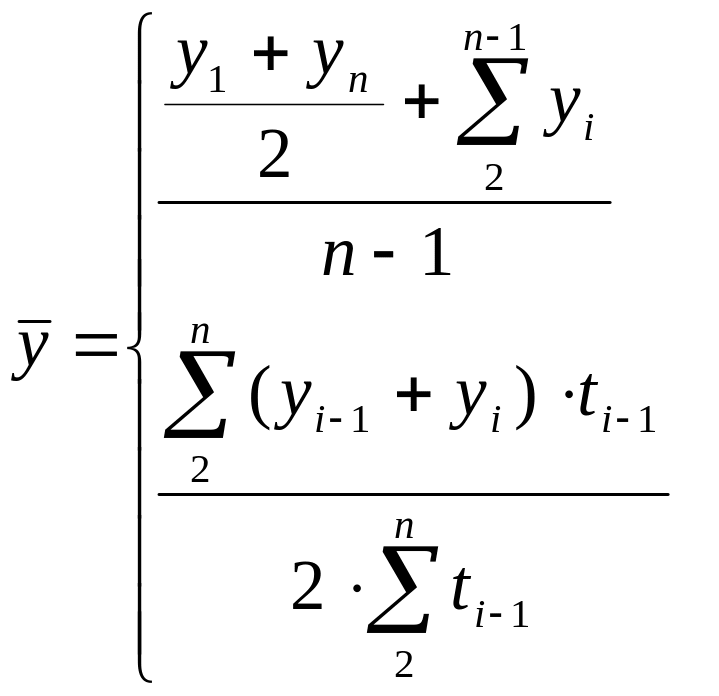6.3. Средние показатели рядов динамики

Для получения обобщающих показателей динамики социально-экономических явлений определяются средние величины: средний уровень ряда, средний абсолютный прирост, средний коэффициент и темп роста, средний темп прироста. Для выявления закономерностей в рядах динамики используются средние показатели, которые рассчитываются на основе цепных, за исключением средних уровней ряда.

Формулы расчета обобщающих показателей в рядах динамики

Название показателя	Расчетная формула
1	2
Средний абсолютный прирост
Средний коэффициент роста, средний темп роста
Средний темп прироста
Коэффициент опережения
равноотстоящие уровни неравноотстоящие уровни Средний уровень интервального ряда
равноотстоящие уровни неравноотстоящие уровни Средний уровень моментного ряда

Иногда можно воспользоваться преобразованными формулами, представленными в данной таблице, если развернуть формулы для первого, второго и третьего показателя:

Четвертый показатель (коэффициент опережения) позволяет сравнивать скорость изменения показателя в разных рядах динамики. Если коэффициент больше единицы, то скорость изменения уровней первого ряда больше скорости изменений второго, и наоборот.

Средний абсолютный прирост оценивает в абсолютных величинах скорость изменения уровней ряда, средний коэффициент, темп роста и прироста – скорость изменения уровней динамического ряда в среднем в относительных величинах.

Так для предыдущего примера =11,04 тыс.руб., , т.е. прибыль в среднем за 1 год увеличивается на 11,04 тыс.руб., что составляет 0,6% в год.

Средний уровень прибыли в год рассчитывается для интервальных рядов с равноотстоящими уровнями и равен =1880,76 тыс.руб.

6.4. Экстраполяция и прогнозирование в рядах динамики.

Важной задачей статистики при анализе рядов динамики является определение основной закономерности (тенденции) развития, присущей тому или иному ряду динамики. Например, за колебаниями продаж различных видов продовольственных товаров в отдельные сезонные периоды может не просматриваться непосредственно тенденция роста (уменьшения) объемов продаж, а должна быть выявлена статистическими методами.

Выявление и характеристика трендов и моделей взаимосвязи создают базу для прогнозирования, определения ориентировочных значений ряда за его пределами в прошлом (ретроспектива) и будущем (перспектива). Этот метод носит название метод экстраполяции. Экстраполяцию в рядах динамики выполняют различными способами, например, экстраполируют ряды динамики выравниванием по аналитическим формулам.

Непосредственное выделение тренда может быть произведено тремя методами:

1. Укрупнение интервалов. Ряд динамики разделяют на некоторое достаточно большое число равных интервалов. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов). Метод укрупнения интервалов, состоит в замене первоначального ряда на ряд уровней, составленный из больших по продолжительности времени периодов, например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции;

2. Скользящая средняя. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Метод скользящей средней состоит в замене первоначального ряда на ряд уровней, рассчитанных по специальной методике. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда (например, трех), затем средний уровень такого же числа уровней, начиная со второго, далее, начиная с третьего и т.д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду от начала к его концу. При этом исходный ряд преобразуется к укороченному ряду;

При нечетном сглаживании полученное среднее арифметическое значение закрепляют за серединой расчетного интервала, при четном этого делать нельзя. Поэтому при обработке ряда с четными интервалами их искусственно делают нечетными, для чего образуют ближайший больший нечетный интервал, но из крайних его уровней берут только 50 %. Недостаток методики сглаживания скользящими средними состоит в условности определения сглаженных уровней для точек в начале и конце ряда. Получают их специальными приемами – расчетом средней арифметической взвешенной.

3. Аналитическое выравнивание. Под этим понимают определение основной проявляющейся во времени тенденции развития изучаемого явления. Развитие предстает перед исследователем как бы в зависимости только от течения времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющийся во времени результат действия всех причинных факторов. Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически. Метод аналитического сглаживания состоит в подборе аналитической зависимости уровней ряда от показателя времени на основе графического изображения ряда в виде линейной диаграммы. В результате приходят к трендовой модели , где f(t) – уровень, определяемый тенденцией развития; _t – случайное и циклическое отклонение от тенденции.

На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции. Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.

Для аналитического сглаживания используются классические функции (полиномы степени, степенная функция и т.д.):

• Линейная зависимость (линейный тренд - ) выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.

• Параболическая зависимость (параболический тренд - 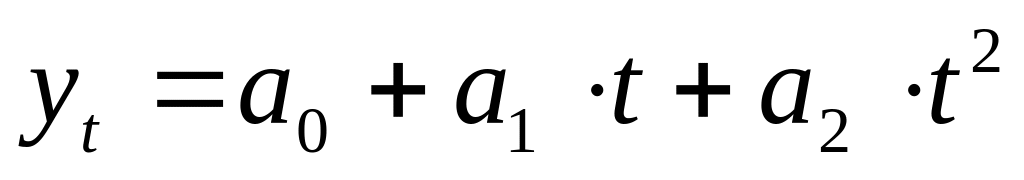) используется, если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют.

• Экспоненциальные зависимости (например, 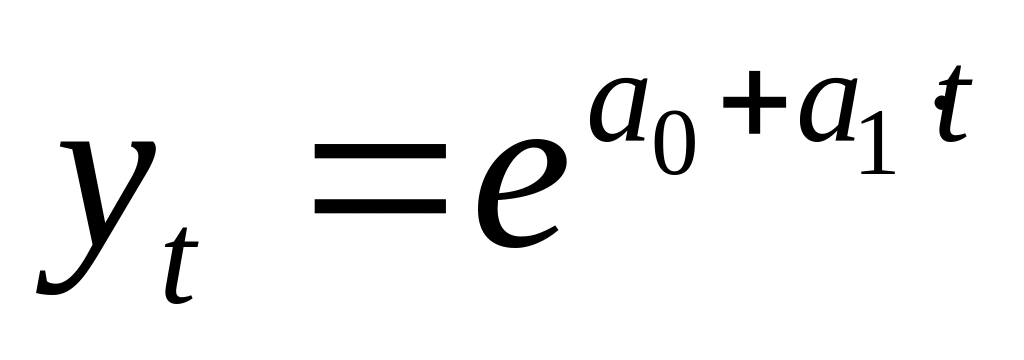) применяются, если в исходном временном ряду наблюдается более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста). При отсутствии такого постоянства – устойчивость в изменении показателей относительного роста (цепных темпов роста и цепных темпов прироста.).

Рассмотрим «технику» выравнивания по прямой . Значения параметров тренда рассчитываются методом наименьших квадратов, рассмотренного в курсе высшей математики. Система нормальных уравнений для линейного тренда имеет вид:

Значения параметров а₀ и a₁ рассчитываются с использованием условных показателей времени t_i, которые задаются самим исследователем. Оценка тренда производится на основе относительной ошибки тренда, величина которой должна быть близка к 6% (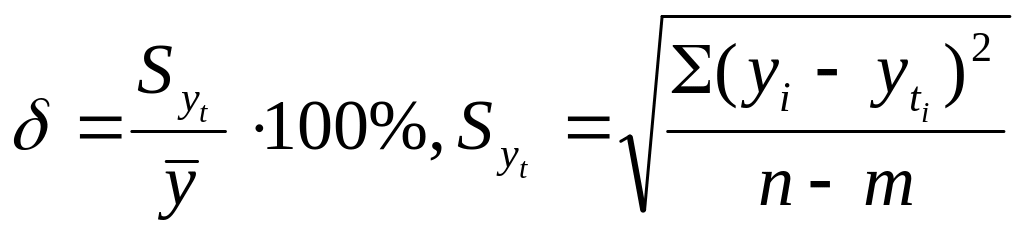 , где - среднее квадратическое отклонение фактических (эмпирических) уровней ряда от теоретических (расчетных), - фактические и теоретические уровни ряда, n-m – число степеней свободы, разность между числом уровней ряда и числом параметров тренда). После оценки тренда можно осуществлять прогнозирование, подставляя вместо t значение, соответствующее прогнозируемому периоду.

Рассмотрим пример:

Год	Прибыль, тыс.у.е.
1994	1561,31
1995	1681,31
1997	1658,69
1998	1446,31
2001	1661,39
2002	1681,41
2003	1780,08
2004	1780,08
2005	1789,08
2006	1876,00
2007	1868,20
2008	1898,08

1. Рассчитать цепные, базисные и средние характеристики ряда, выполнить прогноз на 2011 г. с использованием среднего абсолютного прироста;

2. Построить тренд и на его основе спрогнозировать прибыль на 2011 г.

Решение:

1. Ц епные характеристики, рассчитанные в таблице, показывают периоды увеличения прибыли (1994-1995, 2001- 2006, 2008 г.), причем самый большой рост наблюдался в 2001 г. (увеличение прибыли на 215,08 тыс.руб или на 14,87%, самое большое снижение в 1998 г. – уменьшение прибыли на 212,83 тыс.руб. или на 12,8%). Все базисные характеристики, кроме 1998 г, показывают увеличение прибыли по сравнению с началом изучаемого периода, т.е. 1994 г. 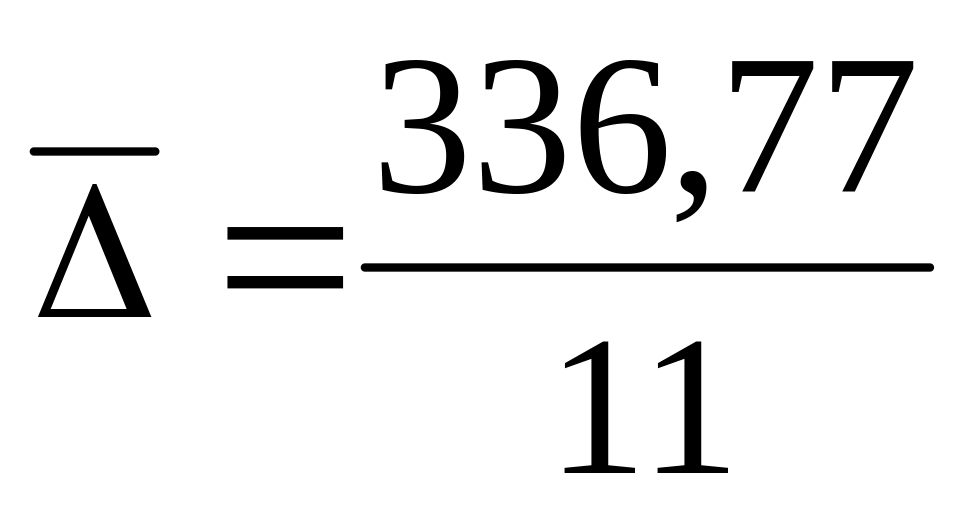Расчет среднего абсолютного прироста = 30,615 тыс.руб. и среднего темпа прироста 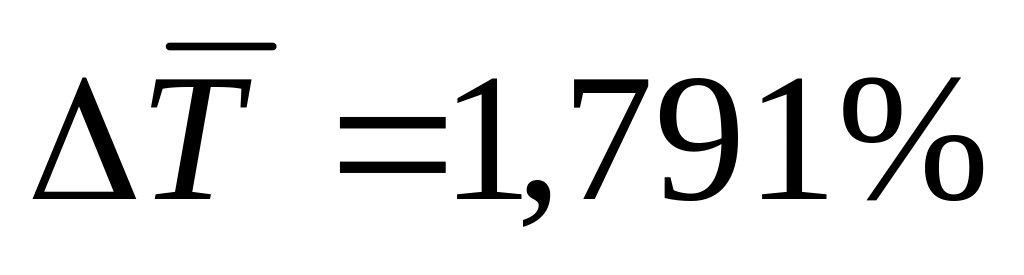показывает среднее увеличение прибыли в год соответственно на 30615 руб. или 1,791%. Средний уровень ряда рассчитывается для интервального ряда с неравноотстоящими уровнями (t –число лет, проходящих между уровнями) 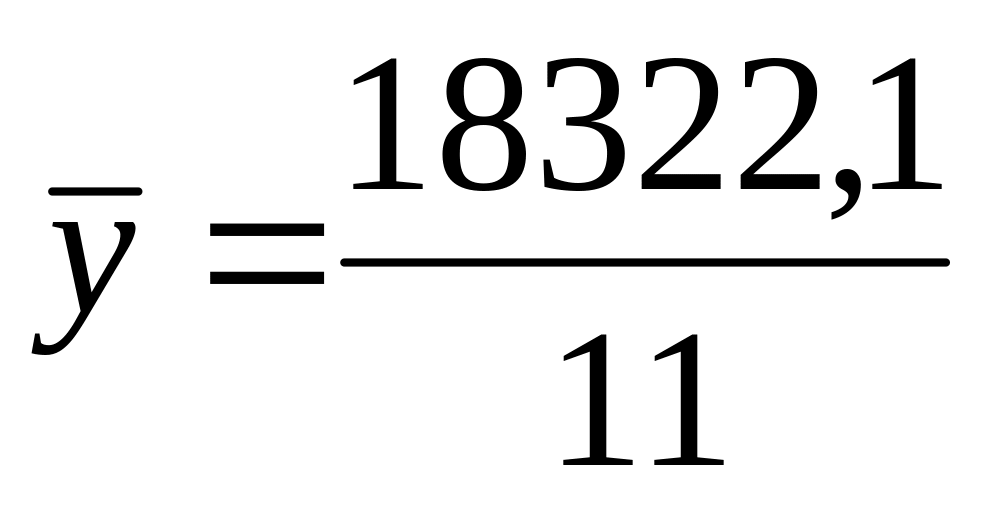=1657,459 тыс.руб. Прогноз на 2011 г. получаем путем прибавления к уровню на 2008 г. среднего абсолютного прироста 3 раза y₂₀₁₁=1898,01+3*30,615=1989,926 тыс.руб.

2. Построим графическое изображение ряда динамики в виде линии:

Все построения для расчетов представлены в таблице. В соответствии с графическим изображением можно предположить линейную зависимость прибыли от показателя времени .

1.

Год	Прибыль, тыс.руб.	i		Ti		Ti		Ai, руб.	ti	yi*ti
		цепной	базисный	цепной	базисный	цепной	базисный
1994	1561,31	-	-	-	-	-	-	-	1	1561,31
1995	1681,31	120,00	120,00	107,69%	107,69%	7,69%	7,69%	15613,1	1	1681,31
1997	1658,69	-22,62	97,38	98,65%	106,24%	-1,35%	6,24%	16813,1	2	3317,38
1998	1446,31	-212,38	-115,00	87,20%	92,63%	-12,80%	-7,37%	16586,9	1	1446,31
2001	1661,39	215,08	100,08	114,87%	106,41%	14,87%	6,41%	14463,1	3	4984,17
2002	1681,41	20,02	120,10	101,21%	107,69%	1,21%	7,69%	16613,9	1	1681,41
2003	1780,08	98,67	218,77	105,87%	114,01%	5,87%	14,01%	16814,1	1	1780,08
2004	1780,08	0,00	218,77	100,00%	114,01%	0,00%	14,01%	17800,8	1	1780,08
2005	1789,08	9,00	227,77	100,51%	114,59%	0,51%	14,59%	17800,8	1	1789,08
2006	1876,00	86,92	314,69	104,86%	120,16%	4,86%	20,16%	17890,8	1	1876,00
2007	1868,20	-7,80	306,89	99,58%	119,66%	-0,42%	19,66%	18760,0	1	1868,20
2008	1898,08	29,88	336,77	101,60%	121,57%	1,60%	21,57%	18682,0	1	1898,08
		336,77							11	18232,10

2.

Год	Прибыль, тыс.руб.	Условные ti	ti*yi	ti2
1994	1561,31	-11	-17174,41	121	1548,951923	152,7220652
1995	1681,31	-9	-15131,79	81	1580,687028	10124,9825
1997	1658,69	-7	-11610,83	49	1612,422133	2140,715529
1998	1446,31	-5	-7231,55	25	1644,157238	39143,52949
2001	1661,39	-3	-4984,17	9	1675,892343	210,3179426
2002	1681,41	-1	-1681,41	1	1707,627448	687,3545562
2003	1780,08	1	1780,08	1	1739,362552	1657,910535
2004	1780,08	3	5340,24	9	1771,097657	80,68247961
2005	1789,08	5	8945,4	25	1802,832762	189,1384692
2006	1876,00	7	13132	49	1834,567867	1716,621634
2007	1868,20	9	16813,8	81	1866,302972	3,598715127
2008	1898,08	11	20878,88	121	1898,038077	0,001757544
	20681,94		9076,24	572	20681,94	56107,57567

Задавая соответствующим образом показатели времени, получаем в системе нормальных уравнений :

 а₀ = 1723,50; а₁ = 15,87.

Уравнение прямой примет вид , для выполнения оценки тренда и последующего его использования рассчитаем теоретические уровни ряда, подставив в полученное уравнение условные показатели времени каждого из уровней. Так как число параметров тренда – 2, а число уровней ряда – 12, то число степеней свободы – 10 и относительная ошибка тренда 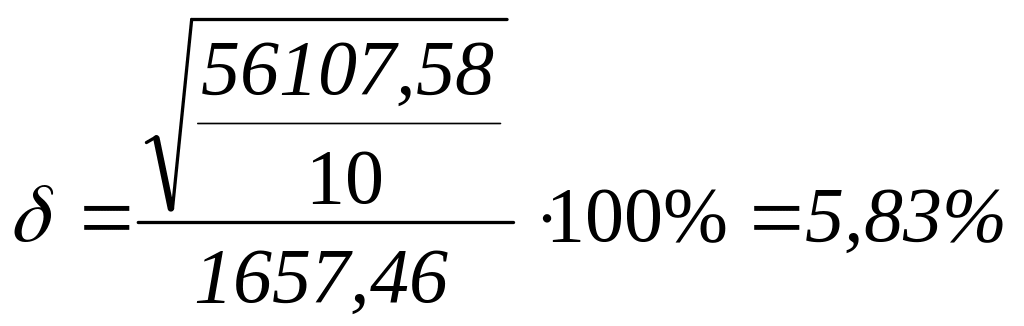, что позволяет сделать заключение о возможности использования тренда для прогнозирования. Прогноз на 2011 г. при t=15, а, следовательно, y₂₀₁₁= 1961,508.

Контрольные вопросы:

1. Для чего нужно изучать динамику явлений?

2. Что характеризуют абсолютные характеристики динамического ряда?

3. Что характеризуют относительные характеристики динамического ряда и каковы формулы для их вычисления?

4. Опишите логику построения цепных и базисных показателей рядов динамики.

5. Какие показатели описывают общую закономерность изменения уровней ряда динамики, запишите формулы для расчета среднего абсолютного прироста, темпа роста и прироста?

6. Какие формулы используются для расчета средних уровней интервальных и моментных динамических рядов?

7. Что представляет собой тенденция ряда динамики?

8. Какие методы сглаживания используются для выявления общей закономерности изменений в уровнях ряда динамики?

9. Как определяется тип уравнения тенденций динамики?

10. Каким образом задаются условные показатели времени при построении тренда?

11. Дайте понятие коэффициента опережения, что он характеризует?

12. Как оценивается возможность использования уравнения тренда для построения прогнозных значений уровней?

13. На какой период можно осуществлять прогноз с использованием тренда?

14. Численность населения одного из регионов РФ в 2008 г. составила 1489,5 тыс.чел., абсолютный прирост составил 10,8 тыс.чел. по сравнению с 2007 г., темп роста – 100,7%. Определить абсолютное значение 1% прироста.

Тесты по теме:

1. Общую тенденцию изменений в уровнях ряда показывают:

а) абсолютный прирост, коэффициент и темп роста, темп прироста, абсолютное значение 1% прироста;

б) средний абсолютный прирост, средний коэффициент и темп роста;

в) все средние характеристики рядов динамики;

г) абсолютный прирост, средний коэффициент и темп роста, темп прироста, абсолютное значение 1% прироста;

д) все цепные характеристики рядов динамики.

2. Для расчета среднего абсолютного прироста используется:

а) средняя геометрическая;

б) средняя арифметическая взвешенная;

в) средняя арифметическая простая;

г) средняя хронологическая.

3. Если цепной темп роста равен 108%, то:

а) наблюдается рост показателя от уровня к уровню 8%;

б) увеличение текущего уровня составило 108%;

в) текущий уровень увеличился на 8% по сравнению с предыдущим;

г) уровень динамики увеличился на 8%.

4. Какая формула используется для расчета средней численности работников предприятия:

Дата (число, месяц)	Число работников
01.01	101
01.02	102
01.03	100
01.04	98

а) ; б) ;

в) ; г) .

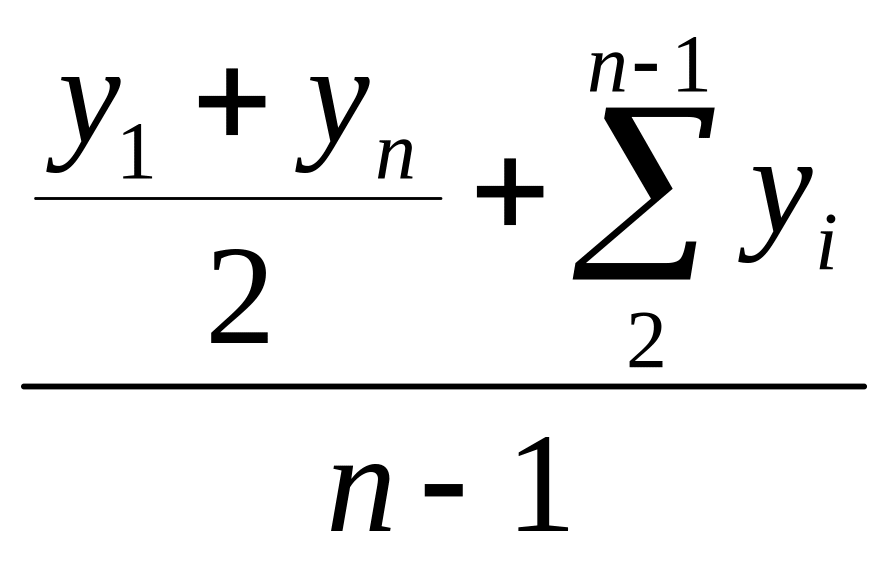5. Какая формула используется для расчета среднегодового выпуска продукции:

Годы	Выпуск продукции, млн. руб.
1997	189
1998	170
2000	102
2003	80
2008	59

а) ; б) ;

в) ; г) .

6. Какая формула используется для расчета средней величины остатков вкладов в банке за изучаемый период:

Дата	Остатки вкладов населения в банке, тыс. у.е.
01.01.08	141,6
01.03.08	144,9
01.04.08	127,3
01.05.08	270,5
01.08.08	208,0

а) ; б) ;

в) ; г) .

7. Если уравнение тренда 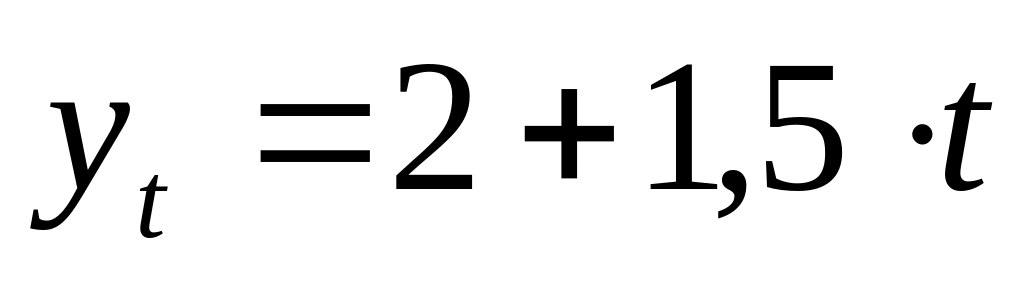, условные показатели времени {-4;-3;-2;-1;0; 1;2;3;4}, периодом для отдельного уровня является год, то каким будет значение уровня ряда через 2 года:

а) 5;

б) 9,5;

в) 11;

г) рассчитать нельзя.

8. Средняя заработная плата в регионе в январе месяце составила 13100 руб., а в июне – на 25% больше. Абсолютный прирост в среднем за месяц равен:

а) 5%; б) 3275; в) 545,83; г) 655.