5.3. Непараметрическое методы оценки связей атрибутивных признаков

Методы КРА не универсальны, они применяются для изучения взаимосвязи количественных признаков. Для исследования взаимосвязи атрибутивных признаков используют непараметрические методы. Оценка силы связи качественных признаков производится на базе коэффициентов ассоциации и контингенции, Пирсона-Чупрова.

В спомогательная таблица для расчета коэффициента взаимной сопряженности

y x	I	II	III	Всего
Итого				n

, , - значения соответствующих категорий, находящихся в указанных местах. Для расчета коэффициентов Пирсона-Чупрова строятся таблицы сопряженности и рассчитываются коэффициенты взаимной сопряженности:

Пирсона ( ) и Чупрова (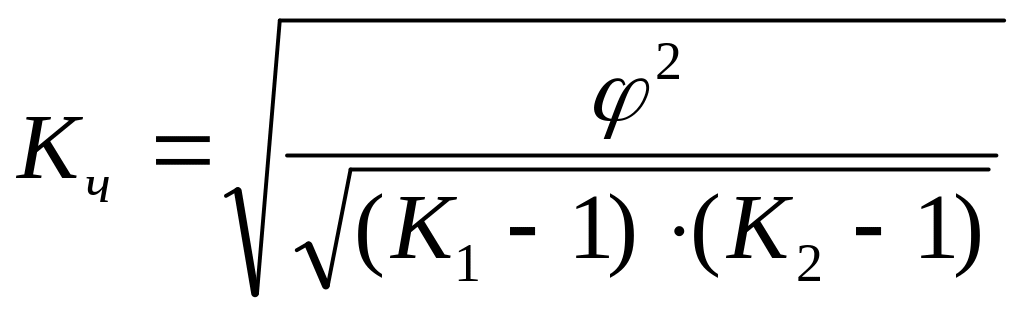 ), где ^ - показатель взаимной сопряженности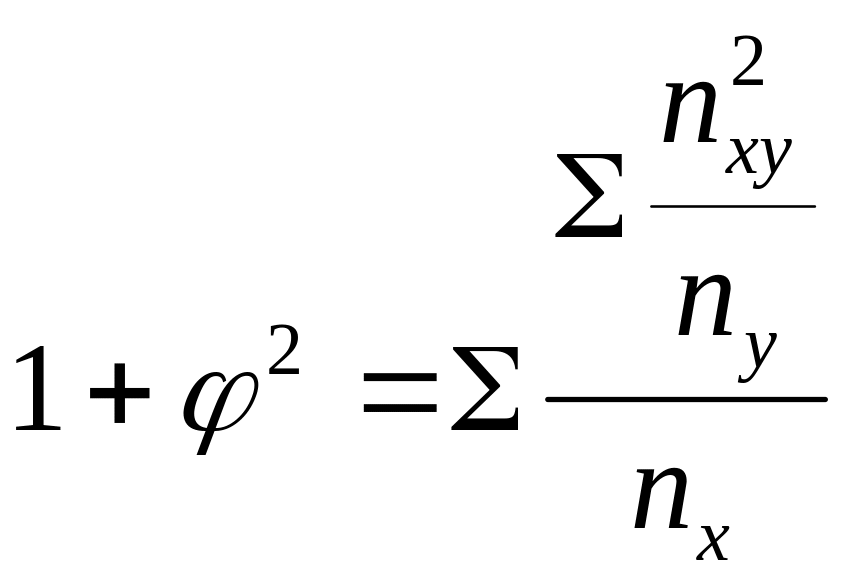 , K₁ – число значений (групп) первого признака, , K₂ – число значений (групп) второго признака.

Коэффициент ассоциации , коэффициент контингенции .

Макет таблицы для расчета коэффициента ассоциации и контингенции

a	b	a+b
c	d	c+d
a+c	b+d	a+b+c+d

Пример. С помощью коэффициента взаимной сопряженности исследуем связь между себестоимостью продукции и накладными расходами на реализацию:

Накладные расходы	Себестоимость			Итого
	Низкая	Средняя	Высокая
Низкие	19	12	9	40
Средние	7	18	15	40
Высокие	4	10	26	40
Итого:	30	40	50	120

= 0,431 + 0,356 + +0,414=1,183  , тогда К_п= =0,39, а К_ч=0,31. Оба коэффициента говорят о средней связи между себестоимостью и накладными расходами на реализацию.

При построении моделей регрессии должны соблюдаться следующие требования:

1. совокупность должна быть однородной и математически описываться непрерывными функциями;

2. факторный признак должен иметь количественное (цифровое) значение;

3. наличие достаточно большого объема исследуемой выборочной совокупности;

4. причинно-следственные связи должны описываться линейной или приводимой к линейной форме зависимостью;

5. отсутствие количественных ограничений на параметры модели связи;

6. постоянство территориальной и временной структуры изучаемой совокупности.

Соблюдение данных требований позволяет построить модель, наилучшим образом описывающую реальные процессы и явления.

Контрольные вопросы:

1. В чем состоит отличие функциональной и стохастической связи?

2. В чем достоинства и недостатки метода параллельных рядов и аналитических группировок?

3. Какие основные задачи решают с помощью корреляционного и регрессионного анализа?

4. Какие виды уравнений регрессии существуют?

5. Что называется корреляционной связью?

6. Какой признак в статистике является факторным?

7. Какой признак в статистике является результативным?

8. Какие коэффициенты используются для оценки связи атрибутивных признаков?

9. Какие формулы используются для расчета коэффициентов в линейном уравнении регрессии?

10. Можно ли строить уравнение парной корреляции для сгруппированных данных?

11. Что показывает коэффициент корреляции и коэффициент детерминации?

12. Для чего используется шкала Чеддока?

13. Каков экономический смысл параметров в уравнении линейной парной корреляции?

14. Какие приемы используются для оценки адекватности линейной регрессионной модели?

15. Охарактеризуйте основные проблемы и правила построения однофакторной линейной регрессионной модели.

16. Исследовалась социально-демографическая характеристика случайных потребителей наркотиков от их семейного положения в одном из регионов РФ (тыс.чел.):

Потребление	Семейное положение
	замужем (женат)	не замужем (не женат)
Потреблял	10,5	14,5
Не потреблял	2,5	4,5

Рассчитайте коэффициенты ассоциации и контингенции, сформулируйте выводы, вытекающие из полученных расчетов.

Тесты по теме

1. Что можно сказать о направлении связи :

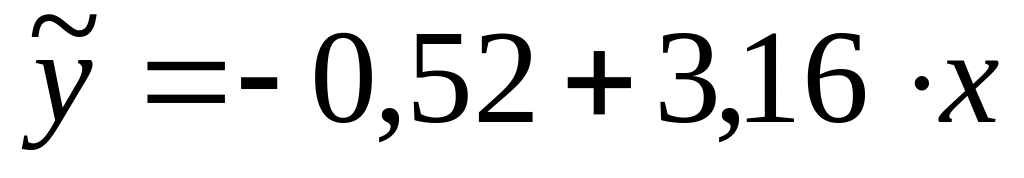а) связь прямолинейная;

б) связь прямая;

в) связь однофакторная;

г) связь криволинейная;

д) связь обратная.

2. Какой вид связи описан уравнением :

а) функциональная однофакторная связь;

б) множественная корреляционная связь;

в) корреляционная криволинейная парная связь;

г) корреляционная линейная парная связь.

3. Если r_xy=-0,7, то, какова сила, направление и теснота связи:

а) связь отсутствует, так как коэффициент корреляции отрицателен;

б) связь линейная, слабая, 49 % изменений результата происходит под влиянием фактора;

в) связь прямая, умеренная, 70% изменений результата происходит под влиянием фактора;

г) связь обратная, сильная, 49 % изменений результата происходит под влиянием фактора.

4. Выберите верные утверждения:

а) стохастическая связь – вероятностным образом определенная связь;

б) функциональная и жестко детерминированная связь разные типы связи;

в) функциональная и статистическая связь это одно и тоже;

г) корреляционная связь – частный случай статистической;

д) уравнение регрессии описывает функциональный вид связи;

уравнение регрессии описывает зависимость условной средней величины результата от фактора.

5. Коэффициенты, использующиеся для изучения связи только атрибутивных признаков (выберите нужные):

а) коэффициент ассоциации;

б) коэффициент Пирсона-Чупрова;

в) коэффициенты взаимной сопряженности;

г) коэффициент контингенции;

д) коэффициент детерминации;

е) линейный коэффициент корреляции.

6. Метод, с помощью которого рассчитываются значения параметров уравнения регрессии:

а) метод параллельных рядов;

б) метод наименьших квадратов;

в) метод аналитических группировок;

г) метод оценки адекватности модели;

д) метод сопоставления рядов.