
- •Астафурова Ирина Сергеевна Статистика.
- •Владивосток
- •Раздел 1 общая теория статистики
- •Глава 1. Предмет, метод и задачи статистики. Статистическая информация.
- •Основные понятия и категории статистики
- •Статистическое наблюдение.
- •Глава 2. Статистическая сводка и группировка.
- •Статистические ряды. Сводка и группировка
- •Формы представления статистических данных
- •Глава 3. Обобщающие показатели в статистике. Выборочное наблюдение.
- •3.1. Абсолютные величины в статистике.
- •3.2. Относительные величины в статистике, их сущность и виды
- •3.3. Средние величины в статистике. Виды средних величин
- •3.4. Структурные средние величины
- •3.5. Меры вариации, их сущность и роль.
- •Среднее квадратическое отклонение для сгруппированных данных.
- •Свойства дисперсии:
- •Среднее значение признака по способу моментов , Дисперсия по способу моментов ,
- •3.6. Показатели асимметрии и эксцесса, центральные моменты распределения
- •Глава 4. Выборочное наблюдение.
- •4.1. Выборочное наблюдение, оценка генеральных параметров
- •4.2. Оптимальный объем выборки. Малая выборка
- •Глава 5. Статистические методы изучения взаимосвязей в статистике. Корреляционно-регрессионный анализ.
- •5.1. Методы изучения связей в статистике
- •5.2. Корреляционно-регрессионный анализ
- •5.3. Непараметрическое методы оценки связей атрибутивных признаков
- •Глава 6. Статистическое изучение динамики.
- •6.1. Понятие ряда динамики, классификация рядов
- •6.2. Цепные и базисные показатели в рядах динамики
- •Пример. Для изучения изменений прибыли предприятия выполнить оценку с помощью цепных и базисных показателей абсолютных и относительных:
- •6.3. Средние показатели рядов динамики
- •Формулы расчета обобщающих показателей в рядах динамики
- •Глава 7. Индексный метод в статистических исследованиях.
- •7.1. Основные понятия, классификации, обозначения
- •7.2. Общие индексы количественных и качественных показателей
- •7.3. Общие индексы средних величин.
- •7.4. Система взаимосвязанных индексов.
- •Раздел II. Социально-экономическая статистика
- •Глава 8. Основные понятия и категории макроэкономической статистики.
- •Объекты макроэкономической статистики
- •Предмет, метод и задачи макроэкономической статистики
- •Основные классификации и группировки в макроэкономической статистике
- •Глава 9. Статистика населения и трудовых ресурсов.
- •9.1. Статистика населения.
- •9.2. Статистика рынка труда
- •Статистика социально-экономического и трудового потенциала
- •Статистика доходов и уровня жизни населения
- •Раздел III. Система национальных счетов
- •Глава 10. Показатели результатов экономической деятельности и методология их расчета в системе национального счетов (снс)
- •Понятие, содержание и общие принципы построения снс
- •Группировки и классификации в системе национальных счетов
- •Методология расчета основных показателей результатов деятельности в снс
- •Глава 11. Статистика национального богатства
- •Система национального счетоводства
- •Текущие счета.
- •Счета накопления.
- •III. Баланс активов и пассивов.
- •Статистика национального богатства. Национально-вещественная структура нб.
- •11.3. Валовой внутренний продукт, национальный доход: методы расчета
- •Метод конечного использования
- •Раздел IV. Статистика предприятия
- •Глава 12. Показатели деятельности предприятия
- •Статистический учет продукции.
- •Система стоимостных показателей.
- •Основные показатели эффекта и эффективности деятельности предприятия.
- •Статистика численности работников и использования рабочего времени
- •Оплата труда
- •Эффективность
- •Производительность труда
- •Глава 13. Основные и оборотные фонды предприятия
- •Виды основных фондов предприятия и виды их оценки.
- •Состояние, движение и эффективность использования основных фондов.
- •Оборотные средства, показатели наличия и эффективности использования.
- •Основные статистические методы анализа деятельности предприятия.
- •Раздел IV. Статистика финансов.
- •Глава 14. Статистика государственного бюджета
- •14.1. Доходы и расходы государственного бюджета
- •14.2. Статистика государственных финансов и налогов
- •14.3. Оценка экономической деятельности сектора государственного управления
- •Глава 15. Статистика цен
- •15.1. Понятие цены, ее виды
- •15.2. Показатели денежного обращения
- •15.3. Инфляция в экономике, сопоставимый вид стоимостных показателей
- •Раздел V. Статистика рынка товаров и услуг.
- •Глава 16. Статистика финансового рынка
- •16.1. Статистика банковской деятельности.
- •16.2. Система показателей кредитов
- •16.3. Статистика биржевой деятельности
- •16.4. Статистика страхового рынка
- •Глава 17. Внешнеэкономическая деятельность
- •17.1. Оценка внешней экономической деятельности
- •17.2. Статистика международной торговли
- •Страна происхождения и Страна назначения: первая - страна, в которой товар или услуга произведена, вторая – страна, куда товар или услуга доставлена;
- •Список рекомендуемой литературы:
- •Основные формулы исчисления общих индексов
Глава 4. Выборочное наблюдение.
4.1. Выборочное наблюдение, оценка генеральных параметров
Статистическая методология исследования массовых явлений различает два способа наблюдения: методом сплошного и несплошного наблюдения. Для исследования части единиц совокупности (проведения несплошного наблюдения) используются три метода: метод основного массива, выборочный и монографический.
Каждый из методов формирует выборочную совокупность или выборку, являющуюся частью всей совокупности. Вся совокупность единиц называется генеральной. Обязательное назначение каждого из методов – распространение результатов исследования части единиц совокупности на совокупность в целом.
Метод основного массива состоит в отборе наиболее крупных единиц совокупности в выборочную совокупность, обладающих изучаемым свойством.
Монографический метод представляет собой отбор одной или нескольких единиц совокупности, подвергающихся более тщательному изучению их свойств.
Выборочный метод представляет собой метод несплошного наблюдения, при котором отбор из основной совокупности выполняется в случайном порядке, в соответствии с научными принципами теории выборочного метода. Основные принципы выборочного метода – случайность отбора (равной возможности попадания в выборку) и репрезентативность, представительство по всем признакам изучаемой совокупности.
Выборочное наблюдение – несплошное наблюдение, выполненное выборочным методом, при котором отобранная часть изучается, а результаты распространяются на всю совокупность.
Главным условием качества первичных данных статистического наблюдения является достоверность и полнота. В проведении ряда исследований наиболее предпочтительным представляется выборочный метод. В основу отбора выборочным методом лежит принцип равной возможности попадания в выборку каждой единицы генеральной совокупности, случайностью отбора.
При любом статистическом исследовании сплошном или несплошном возникают ошибки двух видов: регистрации и репрезентативности. Ошибки регистрации возникают в результате сбора, занесения информации об изучаемом явлении или процессе и могут быть случайными (непреднамеренными, неискажающими общей картины явления) и систематическими (тенденциозными или преднамеренными, умышленно искажающими картину явления). Ошибки репрезентативности присущи только несплошному статистическому наблюдению и возникают в связи с отличием выборочной и генеральной совокупностей.
Условие случайности отбора предупреждает появление систематических (тенденциозных) ошибок и делает возможной оценку ошибки представительства (репрезентативности). Очевидное отличие выборки от генеральной совокупности позволяет сделать вывод о различиях в оценке показателей, характеризующих генеральную совокупность (генеральных параметров) и выборку (выборочных параметров). Это отличие составляет ошибку выборки.
Ошибка выборки (репрезентативности)- разница между значением показателя, полученного по выборке и генеральным параметром. Ошибка выборки оценивается в зависимости от метода отбора повторного или бесповторного. Так повторный метод представляет собой выбор единицы совокупности и возврат ее в основную совокупность после регистрации ее свойств и признаков, при этом выбранная единица может снова служить объектом отбора. При бесповторном отборе единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается, при такой выборке численность единиц генеральной совокупности сокращается.
Основные генеральные параметры, служащие оценке ошибки выборки представлены в таблице:
Характеристики |
Генеральная совокупность |
Выборочная совокупность |
|
N |
n |
|
M |
m |
|
|
|
|
|
|
|
|
|
|
|
|
Основные
генеральные параметры, для которых
выполняется оценка с использованием
ошибки – генеральная средняя (среднее
значение признака в генеральной
совокупности) и генеральная доля (доля
единиц генеральной совокупности,
обладающая изучаемым свойством). Для
этого используются выборочная средняя
(среднее значение признака в выборке)
и выборочная доля (доля единиц выборки,
обладающая изучаемым свойством ),
предельная ошибка выборки (![]() )
и предельная ошибка выборочной доли
(
)
и предельная ошибка выборочной доли
(![]() ).
).
Очевидно,
что генеральный и выборочный параметры
отличаются друг от друга. Так: предельная
ошибка выборочной средней
![]() ,а
предельная ошибка выборочной доли
,а
предельная ошибка выборочной доли
![]() где
где
![]() -
значения средней величины и доли для
выборочной совокупности,
-
значения средней величины и доли для
выборочной совокупности,
![]() -
значения средней величины и доли
генеральной совокупности, отсюда:
-
значения средней величины и доли
генеральной совокупности, отсюда:![]() .
Причем, предельная ошибка выборочной
средней является произведением параметра
функции Лапласа и средней ошибки
выборочной средней (Sx):
.
Причем, предельная ошибка выборочной
средней является произведением параметра
функции Лапласа и средней ошибки
выборочной средней (Sx):
для бесповторного
отбора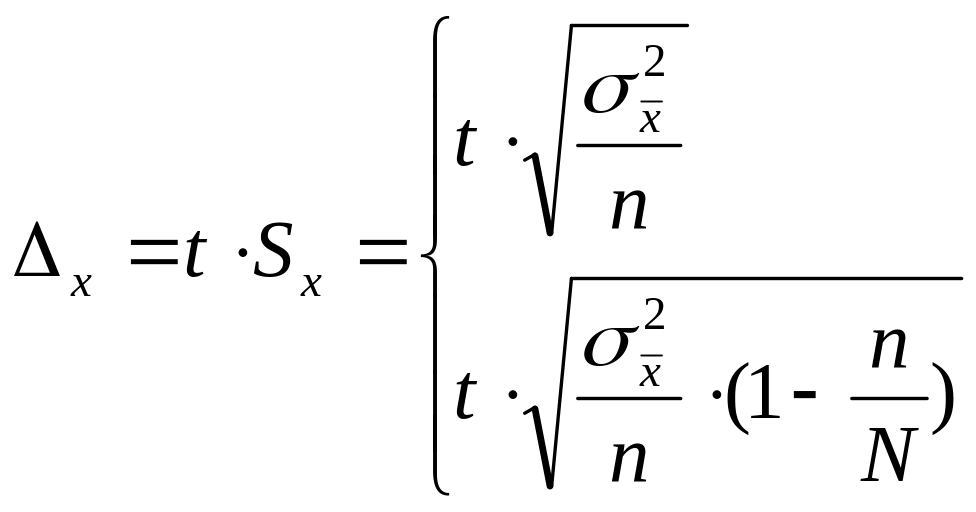
![]() для повторного
отбора
для повторного
отбора
Предельная ошибка выборочной доли является произведением параметра функции Лапласа и средней ошибки выборочной доли (Sw)
для повторного
отбора
для бесповторного
отбора![]()
где n –объем выборки, N – объем генеральной совокупности.
Значение
параметра t
разыскивается по таблице значений
функции Лапласа
![]() (таблица
4), значение
(таблица
4), значение
![]() ,
где m-число единиц
совокупности, обладающих изучаемым
признаком. Некоторые значения функции
Лапласа:
,
где m-число единиц
совокупности, обладающих изучаемым
признаком. Некоторые значения функции
Лапласа:
t |
1 |
2 |
3 |
Ф(t) |
0,683 |
0,954 |
0,997 |
Тогда доверительным интервалом
для генеральной средней будет:
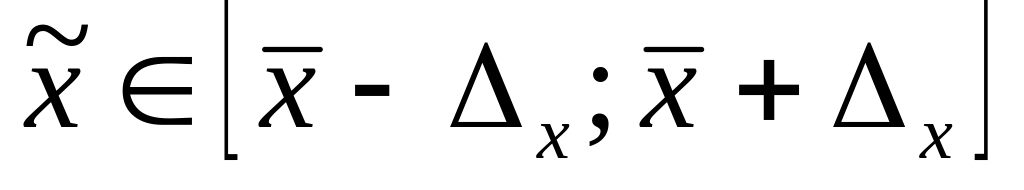 ;
;для генеральной доли, соответственно:
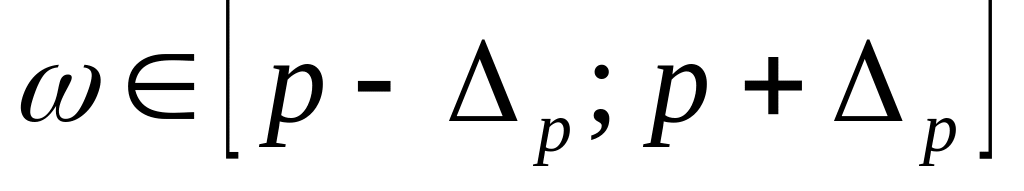 .
.
Рассмотрим пример:
С целью изучения занятости населения города на предприятиях проведена 5%-ная механическая выборка, в результате которой получено следующее распределение предприятий по численности работников:
Группы по численности работников, чел. |
Число предприятий |
|
До |
25 |
15 |
25 |
50 |
20 |
50 |
75 |
35 |
75 |
100 |
25 |
100 |
и выше |
5 |
С вероятностью 0,997 определить ошибку выборочной средней и возможные границы, в которых ожидается средняя численность на предприятиях города.
С вероятностью 0,954 предельную ошибку выборочной доли и границы удельного веса предприятий с численностью работников от 25 до 100 человек.
Рассчитаем выборочную среднюю и дисперсию по способу моментов (ряд является интервальным рядом распределения с равными интервалами), для этого найдем условный ноль и шаг: A =62,5 (середина интервала с максимальной частотой); h=25.
Группы по численности работников, чел. |
Число предприятий |
|
|
|
|
До |
25 |
15 |
-2 |
-30 |
60 |
25 |
50 |
20 |
-1 |
-20 |
20 |
50 |
75 |
35 |
0 |
0 |
0 |
75 |
100 |
25 |
1 |
25 |
25 |
100 |
и выше |
5 |
2 |
5 |
20 |
Итого: |
100 |
|
-15 |
125 |
|
Значения вероятности позволяет по таблице значения функции Лапласа найти значения параметра t, так для расчета предельной ошибки выборочной средней t=3, для расчета предельной ошибки выборочной доли t=2. Так как отбор был бесповторным, то расчет предельных ошибок производится по соответствующим формулам.
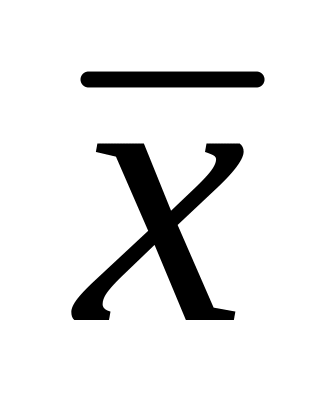 =58,75;
=58,75;
 27,6982;
27,6982;
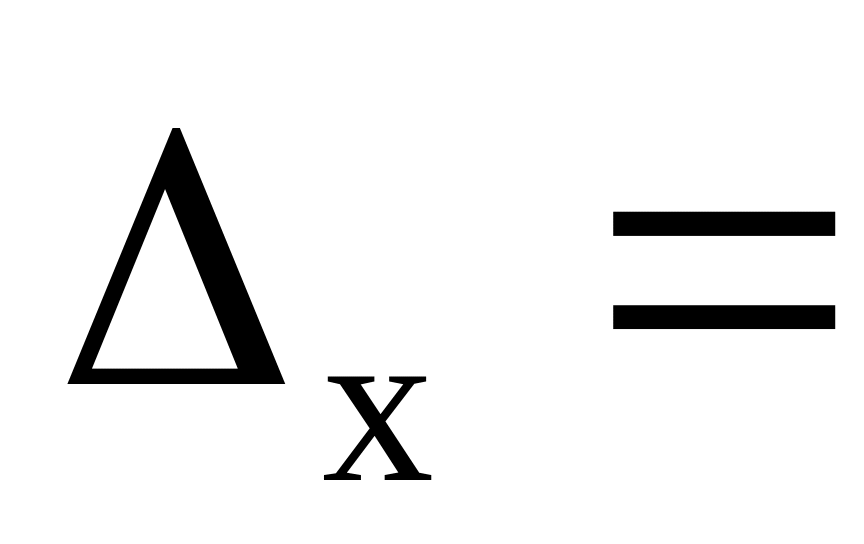 8,099
50,651
8,099
50,651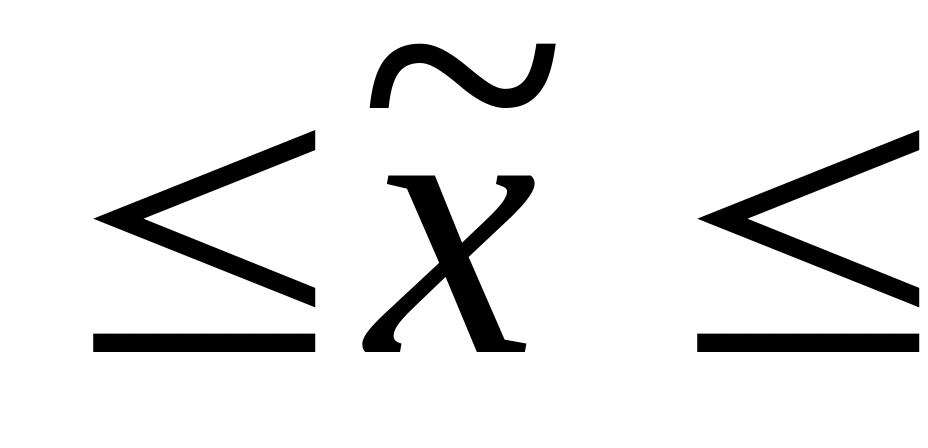 66,849,
средняя численность работников на
предприятиях города от 50 до 67 человек;
66,849,
средняя численность работников на
предприятиях города от 50 до 67 человек;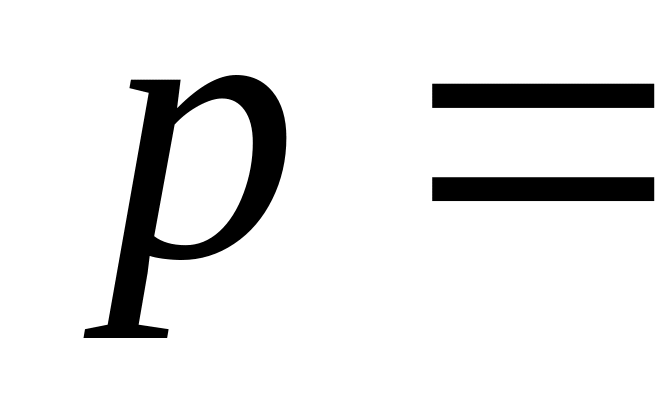 0,800;
0,800;
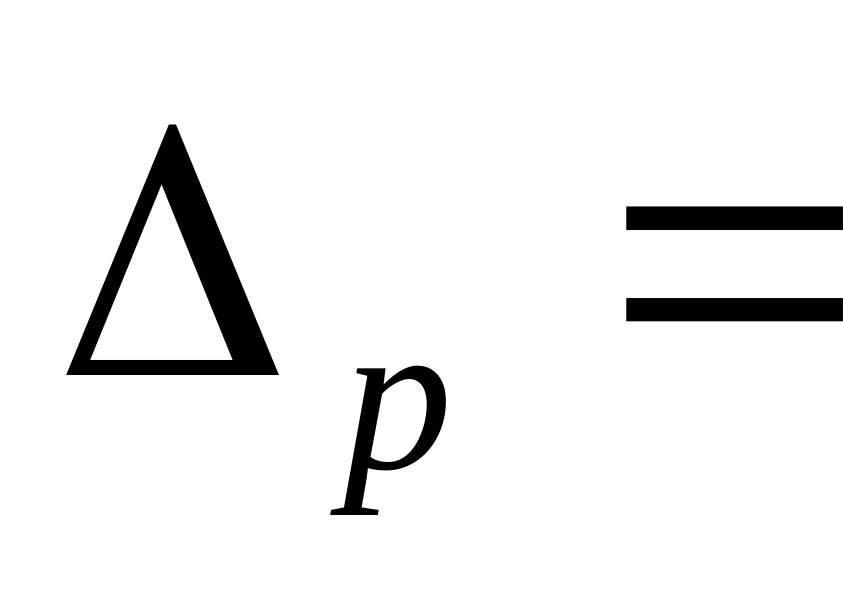 0,077974
72,2%
0,077974
72,2%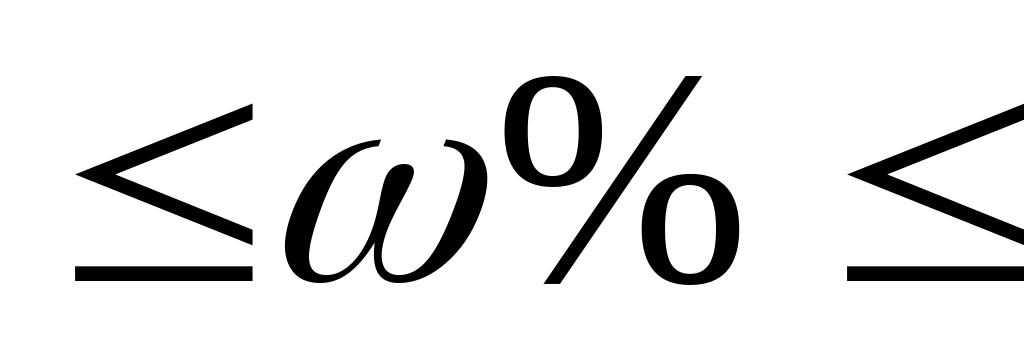 87,8%,
доля предприятий с численностью от 25
до 100 человек на всех предприятиях
города составляет от 72,2% до 87,8%.
87,8%,
доля предприятий с численностью от 25
до 100 человек на всех предприятиях
города составляет от 72,2% до 87,8%.
Существует определенная зависимость между функцией Лапласа, дисперсией и значениями осредняемого признака статистической совокупности (правило 3, так:
если доверительный интервал
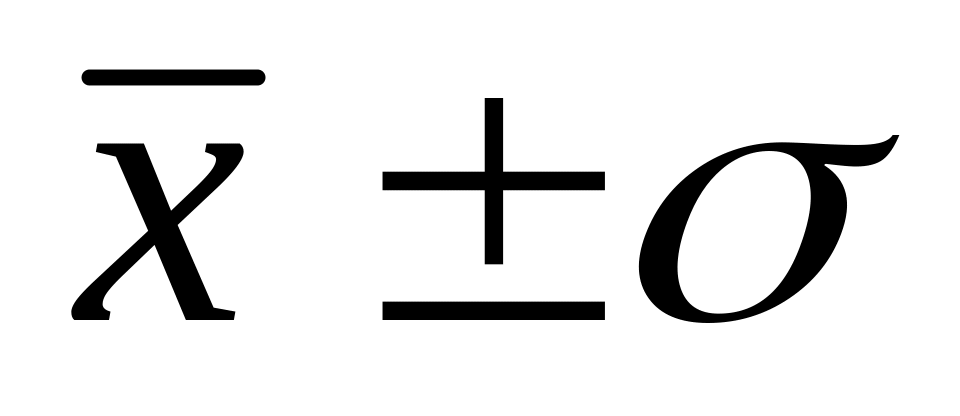 ,
то у 68,3% единиц совокупности значение
признака попадает в указанный интервал;
,
то у 68,3% единиц совокупности значение
признака попадает в указанный интервал;если доверительный интервал
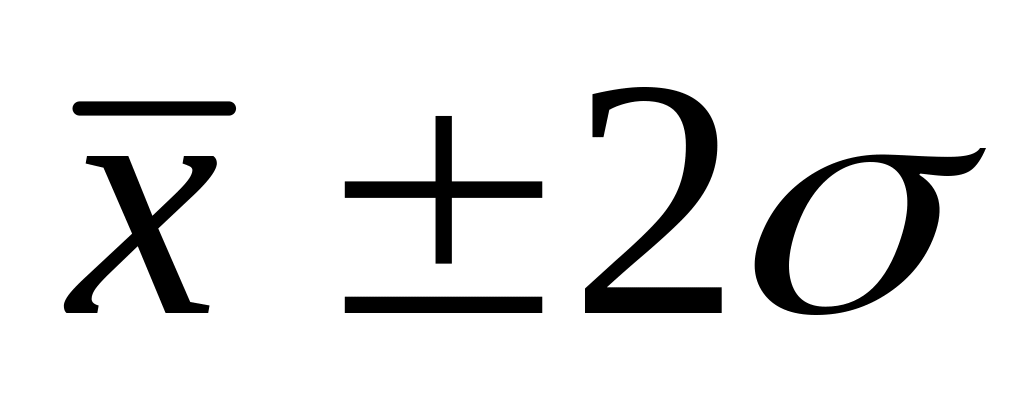 ,
то у 95,4% единиц совокупности значение
признака попадает в указанный интервал;
,
то у 95,4% единиц совокупности значение
признака попадает в указанный интервал;если доверительный интервал
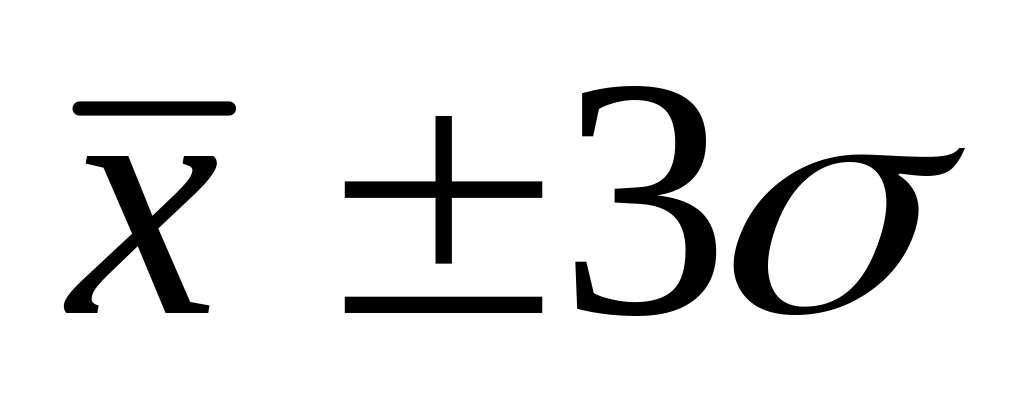 ,
то у 99,7% единиц совокупности значение
признака попадает в указанный интервал.
,
то у 99,7% единиц совокупности значение
признака попадает в указанный интервал.
Основные причины использования несплошного наблюдения: экономия средств и времени, возможность быстрого получения необходимых данных.
