
Кузнецов Л. А / Кратные интегралы. Кузнецов. Вариант 15
.pdf
7 _ 01 _ 15 |
|
|
|
|
|
|
|
|
ru |
|
Изменить порядок интегрирования |
|
|
|
. |
||||||
∫1 dy ∫ f dx +∫e dy ∫1 |
f dx |
|
|
AntiGTU |
||||||
|
|
|
||||||||
0 |
0 |
1 |
ln y |
|
|
|
|
|||
|
|
|
|
|
|
|||||
Решение: |
|
|
|
|
|
|
|
|
||
Построим области интегрирования первого и второго интегралов. |
|
|
||||||||
Сумма повторных интегралов равна двойному интегралу по области D=D1 +D2 . |
||||||||||
Изменяем прядок интегрирования. Т.к внешнй интеграл теперь берем по x, то |
|
|||||||||
проектируем область D=D1 +D2 на ось Ox . При этом получим отрезок [0;1], |
|
|||||||||
концы которого дают пределы интегрирования по x : |
0 и 1. Из уравнений линий |
|||||||||
выражаем y через x. Для x = y : y = x2 , для x = l |
y : y = ex . |
|
|
|||||||
1 |
|
e |
1 |
|
1 |
ex |
|
|
|
|
∫dy ∫ f |
dx +∫dy ∫ |
f dx = ∫dx ∫ f dy |
|
|
|
|||||
0 |
0 |
1 |
ln y |
|
0 |
x2 |
|
|
|
|
Скачано |
с |
|
|
|
|
|
||||
|
|
|
|
|
|
|||||

7 _ 02 _15 |
|
|
|
|
|
|
|
|
ru |
|
|
|
|
|
|
|
|
|
|
||
Вычислить: |
|
|
|
|
. |
|
||||
4 |
|
9 |
|
2 |
|
2 |
|
|
||
∫∫D 5 |
xy + |
|
|
|
x |
y |
|
|
|
|
11 |
|
|
|
|||||||
|
|
|
|
dxdy; |
AntiGTU |
|
|
|||
D : x =1, y = x3 , y = − . |
|
|
||||||||
|
|
|
||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
Построим область интегрирования. Подынтегральная функция - многочлен по x,y, поэтомуее легко интегрировать в любом порядке. Если в повторном интеграле внешний нтеграл взять по y, а внутренний по x, то область интегрирования придется разбивать на части, т.к. левая граница области интегрирования состоит из кусков двух линий. Если же проинтегрировать сначала по y, затем по x, то область не нужно разбивать на части. В этом случае проецируем эту область на ось Ox, получаем отрезок [0;1],
значит, пределы по x равны 0 и 1. Пределы интегрирования по y: |
y = − |
x, y = x3 . |
|||||||||||||||||||||||||||||||||||||
|
4 |
|
9 |
|
|
|
|
|
1 |
x3 |
|
4 |
|
|
9 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
||||
|
|
2 |
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
)dy = ∫dx(2 |
|
|
|
|
|
|
|
x2 y3 ) |
|
|
|
|
||||||||||||
∫∫ |
|
xy + |
|
|
x |
|
y |
|
dxdy = ∫dx ∫ |
( |
|
xy |
+ |
|
|
|
x |
|
y |
|
5 |
xy2 |
+ |
3 |
11 |
|
= |
||||||||||||
5 |
11 |
|
|
5 |
11 |
|
|
||||||||||||||||||||||||||||||||
D |
|
|
|
|
|
|
0 |
− x |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
− x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|||||||||||||||||||
= ∫1 (− 2 x2 |
|
|
3 |
x7 / 2 + 2 x7 |
|
3 x11 )dx = |
( |
−2 |
|
|
x3 + 2 |
|
x9 2 + 1 |
|
|
+ 1 |
|
|
|
|
|
1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
+ |
+ |
15 |
33 |
20 |
x8 |
44 |
x12 |
|
|
= 0 |
|||||||||||||||||||||||||||||
0 |
|
5 |
|
|
11 |
|
|
5 |
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||||||||||
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
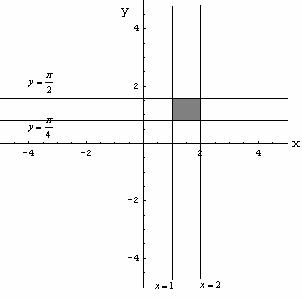
7 _ 03 _15
Вычислить:
∫∫2 y cos 2xy dxdy;
D |
|
|
|
|
|
|
|
|
|
|
AntiGTU |
|||||||||||||||
D : y = π , y = |
π , x =1, |
x = 2. |
|
|
|
|
|
|||||||||||||||||||
|
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если при сведении двойного интеграла повторный интеграл взять по y, . |
||||||||||||||||||||||||||
то для его вычисления придется дважды интегрировать по частям. Чтобы |
||||||||||||||||||||||||||
избежать этого, сначала проинтегрируем по x, затем по y. |
|
|
|
|
|
|
||||||||||||||||||||
|
|
π / 2 |
|
2 |
|
|
|
|
π / 2 |
|
|
|
|
|
|
|
2 |
|
π / 2 |
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∫∫2 y cos 2xy dxdy = 2 ∫ |
ydy∫cos 2xydx = 2 |
∫ |
|
ydy s n2xy |
|
|
|
= 2 |
∫ |
y |
|
(sin 4 y |
||||||||||||||
|
|
|
2 y |
|||||||||||||||||||||||
D |
|
π / 4 |
|
1 |
|
|
|
|
π / 4 |
|
2 y |
|
|
|
1 |
|
π / 4 |
|
||||||||
π / 2 |
|
|
|
|
cos 4 y |
|
π / 2 |
|
|
cos 2 y |
|
π / 2 |
= − |
1 |
− |
1 |
= −1 |
|
||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
− |
|
|
− |
|
|
|
|||||||||||||||||
= ∫ (sin 4 y −sin 2 y)dy = |
|
4 |
|
|
|
− |
|
2 |
|
|
|
2 |
2 |
|
||||||||||||
π / 4 |
|
|
|
|
|
|
|
π / 4 |
|
|
|
|
|
π / 4 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Скачано |
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ru
−sin 2 y)dy =

7 _ 04 _15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вычислить: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||
∫∫∫y |
2 |
|
|
|
πxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
dx dy dz; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
V |
|
|
|
|
2 |
|
|
|
|
|
nAtiGTU |
|
|
|
|
|
|||||||||||||
x |
|
= 0, |
y = −1, y = x, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
V |
|
|
= 0, z = 2π2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Т.к. подынтегральная фунуция не зависит от z, интегрирование нужно начать |
|
||||||||||||||||||||||||||||
по переменной z, при этом пределы интегрирования по z равны 0 и 2π2 . Если |
|
||||||||||||||||||||||||||||
затем интегрировать по y, то придется дважды интегрировать по частям, |
|
|
|
|
|||||||||||||||||||||||||
поэтомупроинтегрируем сначала по x, затем по y. Очевидно, что пределы |
|
|
|
|
|||||||||||||||||||||||||
интегрирования по y будут -1 и 0, по x - y и 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
∫∫∫y |
2 |
|
|
|
πxy |
|
0 |
y |
2 |
0 |
|
πxy |
|
|
2π2 |
2 0 |
y |
2 |
|
2 |
|
|
s n |
πxy |
|
0 |
= |
||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
cos |
dx dy dz = |
∫ |
|
dy∫cos( |
2 |
)dx ∫ dz = 2π |
∫ |
|
dy |
|
|
|
|
2 |
|
|
|
|||||||||||
V |
|
|
|
|
2 |
|
−1 |
|
|
y |
|
|
|
0 |
−1 |
|
|
π y |
|
|
|
|
y |
|
|||||
= −2π |
2 |
0 |
2 2sin(π y2 / 2) |
|
|
|
|
0 |
|
(π y |
2 |
|
−cos |
π y2 |
|
|
0 |
= 4 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
∫y |
π y |
dy = −4π ∫y si |
|
/ 2)dy = −4 |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
−1 |
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|||
Скачано |
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ru

7 _ 05 _15 |
|
|
|
|
|
|
|
|
|
|
|
|
Вычислить: |
|
|
|
|
|
|
|
|
|
|
. |
|
∫∫∫(x2 +3y2 ) dx dy dz; |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
V |
|
|
|
|
ntiGTA U |
|
|
|||||
V : z =10x, x + y =1, |
|
|
|
|
|
|||||||
x = 0, y = 0, z = 0. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
Область интегрирования представляет собой вертикальный цилиндр, |
|
|
|
|||||||||
ограниченный снизуплоскостью z = 0, сверху - поверхностью z =10x. |
|
|
|
|||||||||
Построим проекцию области интегрирования на плоскость Oxy. Пределы |
|
|
|
|||||||||
интегрирования расставляем по рисунку. |
|
|
|
|
|
|
|
|||||
|
|
1 |
1−x |
|
10 x |
1 |
1−x |
+3y2 )dy = |
|
|
||
∫∫∫(x2 +3y2 ) dx dy dz = ∫dx ∫ |
(x2 +3y2 )dy ∫ |
dz =10∫dx ∫ x(x2 |
|
|
||||||||
V |
|
0 |
0 |
|
0 |
0 |
0 |
|
|
|
|
|
1 |
1−x |
|
1 |
|
|
|
|
2 |
+ x4 − 2 x5 |
|
|
1 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||
=10∫xdx(x2 y + y3 ) |
=10∫(x |
|
|
|
|
|
||||||
0 |
−3x2 + 4x3 −2x4 )dx =10 x |
− x3 |
|
|
|
|||||||
0 |
|
0 |
|
|
|
2 |
5 |
|
|
0 |
||
|
|
|
|
|
||||||||
Скачано |
|
с |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
ru
=1

7 _ 06 _15
Найти площадь фигуры, ограниченной данными линиями: y = 32 − x2 , y = −4x.
Решение:
Найдем точки пересечения графиков функций:
32 − x2 |
= −4x |
|
|
|
|
|
|
|
|
|
|
|
|
x2 −4x −32 = 0 |
|
|
|
|
|
|
|
|
|
|
|||
x = 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x = −4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
S = ∫∫dxdy = ∫8 |
dx32∫−x2 |
dy = ∫8 |
dx(y) |
|
32−4−xx2 |
= ∫8 (32 + 4x − x2 )dx = |
|||||||
|
|||||||||||||
D |
|
−4 |
−4 x |
−4 |
|
|
|
−4 |
AntiGTU |
||||
|
2 |
− |
1 |
3 |
|
|
8 |
= 288 |
|
|
|
||
|
|
|
|
||||||||||
|
|
|
|
|
|||||||||
= 32x + 2x |
3 |
x |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
−4 |
|
|
|
|
|||
|
|
|
|
|
|
|
с |
|
|||||
Скачано |
|
|
|
||||||||||
|
|
|
|
|
|||||||||
. |
ru |

7 _ 07 _15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найти площадь фигуры, ограниченной данными линиями: |
|
|||||||||||||||||||||
y2 |
−2 y + x2 |
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y2 |
−6 y + x2 |
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y = x |
3 , x = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AntiGTU |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Два первых уравнения легко преобразовать к виду: |
|
|||||||||||||||||||||
(y −1)2 + x2 =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(y −3)2 + x2 = 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Эти уравнения определяют окружности. |
|
|
|
|||||||||||||||||||
Введем полярную систему координат: |
|
|
|
|
|
|||||||||||||||||
x = r cosϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = r sin ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Окружность y2 −2 y + x2 |
= 0 имеет полярное уравнение |
|
||||||||||||||||||||
r2 sin2 ϕ −2r sin ϕ + r2 cos2 ϕ = 0. |
Откуда r = 2s n ϕ. Аналогично |
|||||||||||||||||||||
y2 |
−6 y + x2 |
= 0 r2 sin2 ϕ −6r sin ϕ + r2 cos2 ϕ = 0 r = 6sin ϕ. |
||||||||||||||||||||
Прямая y = |
x |
имеет полярное уравнение r sin ϕ = r cosϕ |
. |
|||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||
Откуда tgϕ |
= 1 |
|
|
3 |
ϕ =π |
6 |
. Аналогично |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x = 0 r cosϕ = 0 cosϕ = 0 ϕ = |
π |
2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|||
Тогда площадь фигуры будет определяться по формуле: |
|
|||||||||||||||||||||
S = |
∫∫ |
dxdy = π / 2 dϕ |
6 sin ϕ rdr = |
π |
/ 2 dϕ |
r2 |
|
|
|
6 sin ϕ |
= π / 216s n2 ϕdϕ = |
|
||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
∫ |
|
∫ |
|
|
∫ |
|
|
|
|
|
|
|
∫ |
|
|||||
|
|
D |
|
π / 6 |
|
2 sin ϕ |
|
|
π / 6 |
|
2 |
|
|
|
|
|
π / 6 |
|
||||
Скачано |
|
|
|
|
|
|
|
|
2 sin ϕ |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= (8ϕ + 4sin 2ϕ) |
|
π |
3 |
|
3 |
|
|
π |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
=16 |
|
|
+ |
|
|
≈11.84 |
|
|
|
||||||||||
|
π |
|
8 |
|
6 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
. |
ru |

7 _ 08 _15
Пластинка D задана ограничивающими ее кривыми, μ - поверхностная плотность. Найти массупластинки.
D : x = 1 , y = 0, y2 |
= 8x |
(y ≥ 0); |
|
AntiGTU |
||||
2 |
|
|
|
|
|
|||
μ = 7x +3y2 . |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
Из рисунка находим пределы интегрирования по x и y. |
|
|
||||||
Сначала интегрируем по y, затем по x. |
|
|
|
|||||
MD = ∫∫μ(x, y)dxdy =1/∫2 dx ∫8 x (7x +3y2 )dy =1/∫2 dx(7xy + y3 ) |
|
8 x = |
||||||
|
||||||||
D |
0 |
0 |
|
0 |
|
0 |
||
|
|
|||||||
|
|
|
||||||
=1/∫2 30 2x3 / 2 dx = (12 2x5 2 ) |
|
12 = 3 |
|
|
|
|||
|
|
|
|
|||||
0 |
|
|
|
0 |
с |
|
|
|
|
|
|
|
|
||||
Скачано |
|
|
|
|||||
|
|
|
|
|||||
. |
ru |

7 _ 09 _15
Пластинка D задана неравенствами, μ - поверхностная плотность. Найти массу пластинки.
D : x2  4 + y2 ≤1; x ≥ 0, y ≥ 0; μ = 30x3 y7 .
4 + y2 ≤1; x ≥ 0, y ≥ 0; μ = 30x3 y7 .
Решение:
Обобщенная полярная сиситема координат:
x = 2r cosϕ
y = r sinϕ
|
Якобиан перехода равен |
|
|
|
ntiGTUA |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
∂x |
|
∂x |
|
|
|
|
|
2 cosϕ −2r sin ϕ |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
∂ϕ |
∂r |
|
|
|
= |
|
|
= 2r |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
∂y |
|
∂y |
|
|
|
|
|
sin ϕ |
r cosϕ |
|
|
|
|
|
|
|
|
|
||||
|
|
∂ϕ |
∂r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
π / 2 |
1 |
|
|
|
|
|
|
|
|
|
m = ∫∫m(x, y) dx dy = |
∫ dϕ |
∫2r 30 8r3 cos3 ϕ r7 sin7 ϕ dr = |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
D |
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
π |
|
|
|
|
|
|
= |
π |
/ 2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
r |
6 |
1 |
|
= |
|||
∫ |
cos3 ϕ sin7 ϕ dϕ ∫480 r5 dr = −∫cos3 ϕ d(cosϕ) 480 |
|
| |
|
||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
с |
0 |
|
6 |
0 |
|
||
|
|
|
|
|
|
cos4 ϕ |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
|
− |
2 |
|
80 = 20 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
4 |
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
. |
ru |

7 _10 _15 _1
Найти объем тела, заданного ограничивающими его поверхностями:
x2 + y2 = 8, x = 2 y, x = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
z = 30 y 11, |
z = 0. |
|
|
|
|
|
|
|
|
|
|
AntiGTU |
||||||||||||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
2 |
|
8−y2 |
|
30 y /11 |
|
|
|
30 |
|
2 |
|
|
8 |
− |
x |
2 |
|
30 |
|
2 |
|
y2 |
|
|
|
||||
|
∫∫∫ |
|
|
|
|
|
∫ |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||
V = |
|
|
|
∫ |
|
|
|
|
|
|
|
∫ |
|
|
|
∫ |
|
|
|
y dy = |
|
|
∫ |
|
|
|||||||||||
|
|
dx dy dz = |
|
|
dy |
|
dx |
|
dz = |
11 |
|
|
|
dx |
|
|
|
|
|
|
11 |
|
|
|
2 |
| |
|
dx = |
||||||||
|
G |
|
|
|
|
|
0 |
|
2 y |
|
0 |
|
|
|
|
0 |
|
|
|
x2 |
|
|
|
|
|
0 |
|
x |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
= 30 |
|
8 − x2 − x |
|
dx = 30 |
8x − x |
|
− |
x |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
4 |
3 |
5 |
|
| =16 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
22 |
∫ |
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
4 |
|
3 20 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скачано |
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ru
