
Кузнецов Л. А / Векторный анализ. Кузнецов. Вариант 28
.pdf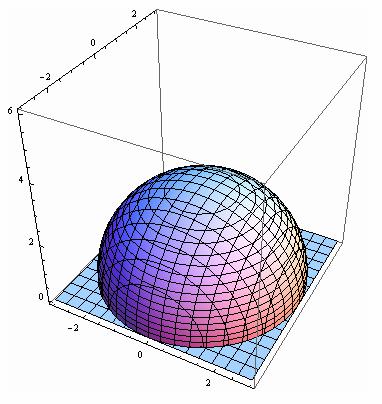
8 _ 04 _ 28 _1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
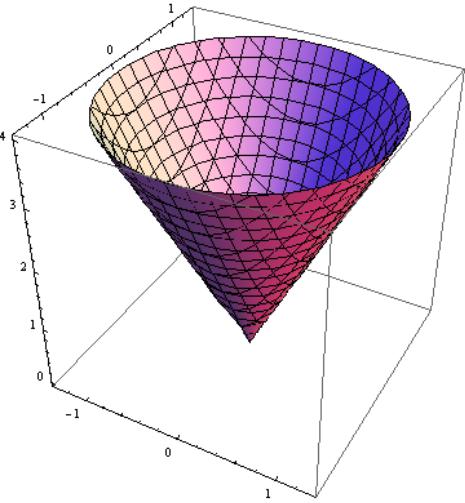
a = (x + xz2 )i + yj +(z − zx2 )k, |
|
S : x2 + y2 |
+ z2 =9, P : z = 0 |
|
(z ≥ 0). |
|||||||||||||||||||||||||||||||||||
П = Пн + Пбок |
Пбок |
= П − Пн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
G G |
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
∂a |
|
|
|
|
∂ay |
|
∂a |
|
|
|
|
|
|
||||||
П = ∫∫ |
(a, n)dS = ∫∫∫div a dx dy dz = ∫∫∫ |
|
x |
|
+ |
|
|
|
|
|
+ |
|
|
z dx dy dz = |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
S |
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
V ∂x |
|
|
|
|
|
AntiGTU |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
∂z |
|
|
|
|
|
|||||||||||
= ∫∫∫(1 + z2 +1 +1 − x2 )dx dy dz = ∫∫∫(3 + z2 |
− x2 )dx dy dz = |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = r cosθ cosϕ |
|
2π |
|
|
|
π |
/ 2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
y = r cosθ sinϕ |
= ∫dϕ |
|
∫ dθ∫r2 cosθ (3 + r2 s n2 θ −r2 cos2 θ cos2 ϕ) dr = |
||||||||||||||||||||||||||||||||||||
|
|
z = r sinθ |
|
|
|
0 |
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2π |
|
π / 2 |
|
|
|
|
|
|
r |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||
= ∫dϕ |
∫ |
dθ |
r3 cosθ + |
|
|
|
(sin2 θ cosθ −cos3 θ cos2 ϕ) |
| = |
|
|
|
|
|
|||||||||||||||||||||||||||
|
0 |
|
0 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||
|
2π |
|
π / 2 |
|
|
|
|
243 |
(sin |
2 |
θ cosθ −(1 −sin |
2 |
θ) cosθ cos |
2 |
ϕ) |
|
||||||||||||||||||||||||
= ∫dϕ |
∫ |
27 cosθ + |
|
5 |
|
|
|
|
|
dθ = |
||||||||||||||||||||||||||||||
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2π |
|
|
|
|
θ + |
243 |
sin3 θ |
|
−sinθ cos |
2 |
ϕ + |
sin3 θ |
cos |
2 |
|
π / 2 |
= |
||||||||||||||||||||||
= ∫dϕ |
27sin |
5 |
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
ϕ |
| |
|
|||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||||||||
= |
2π |
|
|
81 |
|
|
|
|
|
|
|
|
|
27ϕ |
− |
81 |
|
sin 2ϕ |
2π |
|
= 54π |
|
|
|
|
|
|
|
||||||||||||
|
∫0 |
27 − |
5 |
cos 2ϕ dϕ = |
|
|
5 |
|
2 |
|
| |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
G |
|
|
|
|
G |
|
|
|
|
|
|
|
G |
|
G |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
nн = (0;0;1); a |
nн |
= z − zx |
2 ;(a |
nн ) |z=0 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Пн = ∫∫(aG nG |
н )dS = ∫∫0 dS = |
0 |
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
S |
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пбок |
= П − Пн |
= 54π −0 = 54π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
. |
ru |
8_04_28_2 |
|
|
. |
ru |
|
|
|
|
|
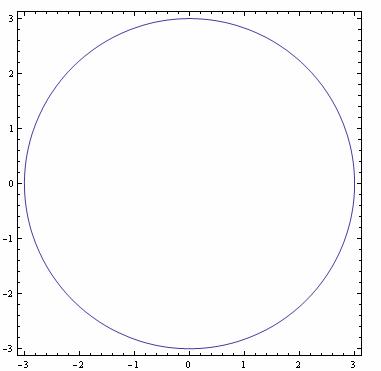
Проекция на плоскость OXY |
|
|
|
|
Скачано |
с |
AntiGTU |
|
|
|
|
|
||
|
|
|
|
8 _ 05 _ 28 _1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
a = 2xi +3yj + 4zk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
P : 2x +3y + z =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
nG ={2;3;1}; |
|
nG |
|
|
|
= |
|
|
nx2 |
+ ny2 + nz2 |
= |
|
|
14 |
AntiGTU |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ny |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||
cosα = |
|
Gx |
|
|
|
= |
|
|
|
|
|
;cos β = |
|
G |
|
= |
|
|
|
;cos |
γ = |
|
Gz |
|
= |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
14 |
|
|
|
|
14 |
|
14 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||||||||
dS = 1 + zx′ 2 + z′y |
2 dx dy = 1 + −2 2 + −3 2 dx dy = 14 dx dy |
|||||||||||||||||||||||||||||||||||||||||||
|
|
GG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosα + ay cos β + az cosγ )dS = |
|
|
|
|
|
|||||||||||||||||||||
П = ∫∫andS = ∫∫(ax |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
S |
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= ∫∫ |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
= ∫∫(2ax +3ay + az )dx dy = |
||||||||||||||
ax |
|
|
|
|
|
|
|
|
|
|
+ ay |
|
|
+ az |
|
|
|
|
|
|
|
|
14 dx dy |
|||||||||||||||||||||
|
|
14 |
|
|
14 |
|
4 |
|
|
|||||||||||||||||||||||||||||||||||
|
Dxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dxy |
|
|
|
|
|
|||||||||||||||
= ∫∫(2 2x +3 3y + 4(1 −2x −3y))dx dy = ∫∫(4 −4x −3y)dx dy = |
||||||||||||||||||||||||||||||||||||||||||||
|
Dxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dxy |
|
|
|
|
|
|
|
|
|
|
|
|
1/ 2 |
(1−2 x) / 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ 2 |
|
|
|
|
|
|
|
|
|
|
|
/ 2) |
(1−2 x) / 3 |
|
|||||||||||||
= ∫ dx ∫ |
|
|
|
|
(4 −4x −3y)dy = |
∫ |
dx (4 y −4xy − |
3y2 |
| |
= |
||||||||||||||||||||||||||||||||||
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
1/ 2 |
|
2 |
− |
10x |
+ |
7 |
|
|
2x3 |
− |
5x |
2 |
7x |
1/ 2 |
= |
1 |
|
|
|
|
|
|
|||||||||||||||||||||
∫ |
2x |
|
|
|
|
3 |
|
|
dx = |
3 |
|
|
3 |
+ |
6 |
|
| |
4 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||||||||
Скачано |
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
. |
ru |
8_05_28_2
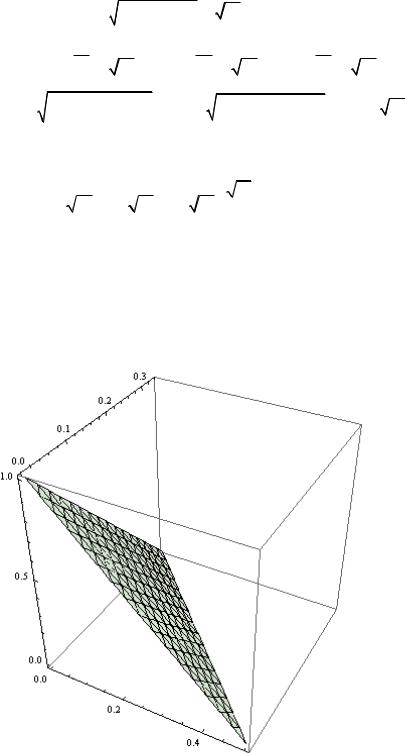
Проекция на плоскость OXY
0.30
0.25
0.20
0.15
0.10
0.05
0.00
0.0 |
0.1 |
0.2 |
0.3 |
Скачано |
с |
|
AntiGTU |
|
0.4 |
0.5 |
. |
ru |
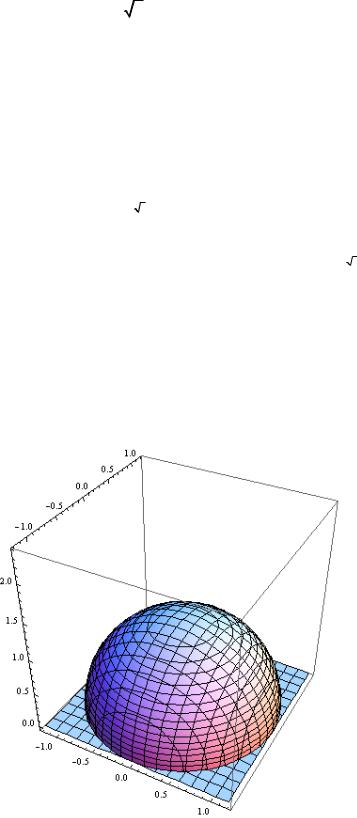
8G_ 07 _ 28 _1G G G a = (3yz − x)i +(x2 − y) j +(6z −1)k
|
2 |
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S : z |
|
= 9(x |
|
+ y |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
z = 4 |
|
|
|
|
|
|
|
ntiGTA U |
||||||||||||||||||||||
Т.к. поверхностьзамкнутая, товоспользуемсяформулой |
|
|
. |
|||||||||||||||||||||||||||
Остроградского− Гаусса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂a |
|
|
|
∂ay |
|
|
|
∂a |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
П = w∫∫a n dσ = ∫∫∫div a dx dy dz = ∫∫∫ |
|
x |
+ |
|
|
|
|
+ |
|
z |
dx dy dz = |
|
|
|||||||||||||||||
∂x |
|
∂y |
|
|
∂z |
|
|
|||||||||||||||||||||||
|
σ |
|
|
|
|
|
|
|
|
V |
|
V |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x = r cosϕ |
|
|
= 42∫π dϕ |
4∫/ 3 r dr ∫4 |
|
||||||||||||||||||||||||
= ∫∫∫(−1 −1 +6)dx dy dz = 4∫∫∫dx dy dz = |
|
dz |
||||||||||||||||||||||||||||
V |
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
y = r sinϕ |
|
|
|
|
0 |
|
0 |
3r |
|
||||||
2π |
|
4 / 3 |
|
|
|
|
|
|
2π |
|
−r3 ) |
| |
|
= 128 |
2π |
|
|
256 π |
|
|
||||||||||
= 4 ∫dϕ ∫ (4r −3r2 ) dr = 4 ∫dϕ(2r2 |
|
∫dϕ = |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 / 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
0 |
|
|
0 |
|
|
27 |
0 |
|
|
|
|
27 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Скачано |
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ru

8_07_28_2
Проекция на плоскость OXY
1.0
0.5
0.0
0.5
1.0
1.0 0.5
Скачано
с
0.0 |
AntiGTU |
|
0.5 |
1.0 |
|
. |
ru |
8G |
_ 09 _ 28G_1 G |
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
a |
= 2xy +i + 2xy j |
+ z2 k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
x |
|
+ y |
|
+ z |
|
= |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
: |
|
2 |
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0(z ≥ 0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nAtiGTU |
|||||||||||||||||
Т.кповерхнлстьзамкнутая, товоспользуемсяформулойОстроградского |
. |
|||||||||||||||||||||||||||||||
|
|
|
|
G G |
|
|
|
|
G |
|
|
|
∂a |
|
|
∂ay |
|
|
|
∂a |
|
|
|
|||||||||
П = w∫∫(a; n)dS = ∫∫∫div a dx dy dz = ∫∫∫ |
|
x |
+ |
|
|
|
|
+ |
|
|
|
z |
dx dy dz = |
|
||||||||||||||||||
∂x |
|
∂y |
∂z |
|
||||||||||||||||||||||||||||
|
|
|
S |
|
|
|
|
|
|
V |
|
|
|
V |
|
|
|
|
|
|
|
|
||||||||||
= ∫∫∫(2x + 2 y + 2z )dx dy dz = 2∫∫∫(x + y + z )dx dy dz = |
|
x = r cosθ cosϕ |
|
|
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
|
y = r cosθ sinϕ |
= |
|
|||||||||||||||||||||||||||||
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = r sinθ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2π |
|
π / 2 |
|
|
|
|
4 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= 2 ∫dϕ ∫ |
|
cosθ dθ ∫r3 (sinθ +cosθ cosϕ +cosθ s |
|
|
|
ϕ)dr = |
|
|
||||||||||||||||||||||||
|
|
0 |
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
π / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
4 |
|
4 2 |
|
|
|
|
|
|
||||
= 2 ∫dϕ ∫ |
|
(sinθ cosθ +cos2 θ(cosϕ +sinϕ)) dθ |
|
|
|
| |
= |
|
|
|
||||||||||||||||||||||
|
4 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
= |
2∫π dϕ |
π∫/ 2 |
(sinθ cosθ +1 +cos 2θ |
(cosϕ +sinϕ)) dθ = |
|
|
|
|
|
|
||||||||||||||||||||||
|
0 |
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2π |
|
sin2 θ |
|
|
θ |
+ |
sin 2θ |
|
|
ϕ) |
|
π / 2 |
= |
2π |
|
1 |
+ |
π(cosϕ +sinϕ) |
|
||||||||||||
|
dϕ |
|
|
2 |
+ |
2 |
4 |
(cosϕ +sin |
|
| |
|
∫0 |
|
|
2 |
4 |
dϕ = |
|||||||||||||||
|
∫0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||||
= |
|
ϕ |
+ |
π(sin−cos |
ϕ) |
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
4 |
|
|
|
|
| =π |
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ru
8_09_28_2
Проекция на OXY
2 

1
0
1
2
2 |
1 |
0 |
Скачано |
с |
|
AntiGTU |
|
1 |
2 |
. |
ru |
8 _10 _ 28 |
|
|
|
|
|
|
|
|
F = −xi + yj, |
|
|
|
|
|
|
||
L : x2 + |
y2 |
=1 |
(x ≥ 0, y ≥ 0), |
|
|
|||
|
|
|
||||||
9 |
|
|
|
|
|
|
|
|
M (1, 0), N (0,3). |
|
|
|
|
|
|||
A = ∫(Fx dx+ Fy dy) = |
|
|
x = cos t |
|
= π∫/ 2 |
|||
|
|
|||||||
L |
|
|
|
y = 3sin t |
|
0 |
||
π / 2 |
|
|
|
π / 2 |
|
|
||
= ∫ 10sin t cos t dt = |
|
|
|
|
||||
5sin2 t | |
= 5 |
|||||||
0 |
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
Скачано |
с |
|
(−cosAntiGTUt (−s n t) +3sin t 3cos t) dt =
. |
ru |
8 _11_ 28 _1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ru |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a = xi −3z2 j + yk, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||
|
x =cos t, y = 4 sin t, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Г: |
− 4sin t + 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
z = 2 cos t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
dx = −sin t dt; dy = 4 cos t dt; dz |
= (−2sin t − 4 cos t) dt |
AntiGTU |
|
|
|
|
|
|
|||||||||||||||||
Ц = v∫(ax dx+ ay dy+ az dz)= |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2∫π (cos t(−sin t) −3(2 cos t − 4 sin t + 3)2 4 cos t + 4 sin t(−2 sin t − 4 cos t))dt = |
|
|
|
|
|
|
|
|||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2∫π (−108cos t −144 cos2 t − 48cos3 t + 271sin t cos t +192 cos2 t sin t −8sin2 t −192sin2 t cos t )dt = |
|
|
|
|
||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2∫π (−108cos t −144 cos2 t − 48(1 −sin2 t) cos t + 271sin t cos t +192 cos2 t sin t − 4(1 − cos 2t) −192sin2 t cos t) dt = |
||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
144 |
sin 2t |
− 48sin t + |
48 |
sin |
3 |
t + |
271 |
s |
2 |
t − |
192 |
cos |
3 |
t − 4t + 2 sin 2t − |
192 |
sin |
3 |
t |
|
2π |
= |
||
−108sin t − |
t + |
2 |
|
3 |
|
2 |
|
3 |
|
|
3 |
|
|
| |
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||
= −152π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скачано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.0 |
|
|
0.5 0.0 |
0.5 |
1.0 |
|
||
|
|
