
- •Скачано с http://antigtu.ru
- •Задача Кузнецов Дифференциальные уравнения 1-20
- •Задача Кузнецов Дифференциальные уравнения 3-20
- •Задача Кузнецов Дифференциальные уравнения 6-20
- •Задача Кузнецов Дифференциальные уравнения 10-20
- •Задача Кузнецов Дифференциальные уравнения 11-20
- •Задача Кузнецов Дифференциальные уравнения 12-20
- •Задача Кузнецов Дифференциальные уравнения 13-20
- •Задача Кузнецов Дифференциальные уравнения 14-20
- •Задача Кузнецов Дифференциальные уравнения 15-20
- •Задача Кузнецов Дифференциальные уравнения 16-20

Скачано с http://antigtu.ru
Задача Кузнецов Дифференциальные уравнения 1-20
Условие задачи |
|
|
|
. |
|
|
|
|
|
|
|
Найти общий интеграл дифференциального уравнения. (Ответ представить в виде |
|||||
|
): |
|
|
antiGTU |
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
Подставляя в исходное уравнение |
|
, получим: |
|
||
Интегрируем обе части уравнения, получим: |
|
|
|||
|
Скачано |
с |
|
|
|
|
|
|
|
||
Задача Кузнецов Диффере циаль ые уравнения 2-20 |
|
||||
Условие задачи |
|
|
|
|
|
Найти общий интеграл дифференциального уравнения. |
|
||||
Решение |
|
|
|
|
|
Поделим обе части равенства на |
: |
|
|
|
|
 ;
;
ru

|
. |
|
|
|
|
. |
ru |
|
|
|
|
|
|
|
|
В последнем равенстве внесем под корень: |
antiGTU |
|
|
||||
|
; |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
Поскольку удалось записать уравнение |
|
в виде |
|
, то данное уравнение — |
|||
однородное дифференциальное уравнение. |
|
|
|
|
|
||
Введем в рассмотрение новую неизвестную функцию |
где |
. Тогда |
|||||
уравнение |
. Подставляя выражения |
|
и через новую неизвестную функцию в |
получим |
|||
|
|
|
|
|
|
|
|
|
; |
|
с |
|
|
|
|
Из последнего уравнения выразим : |
|
|
|
|
|
||
Скачано |
|
|
|
|
|
|
|
Как видим, |
предст вляет собой уравнение с разделяющимися переменными. Разделим |
||||||
переменные в |
. Для этого умножим обе части равенства |
на |
: |
|
|||
Проинтегрируем обе части равенства |
: |
|
|
|
|
|
|

Интегралы в последнем равенстве могут быть легко вычислены (хотя вычисления и займут довольно таки много времени). Например, интеграл в левой части равенства вычисляется заменой переменной  на косинус гиперболический, а интеграл в правой части равенства является табличным. В результате получим:
на косинус гиперболический, а интеграл в правой части равенства является табличным. В результате получим:
|
|
|
, где — произвольная постоянная |
. |
ru |
|
Используя свойства логарифмов можем упростить выражение: |
||||||
|
|
; |
|
|
||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
Вспоминая, что |
приходим к ответу: |
|
|
|
||
или, если домножить на |
обе части равенства: |
|
|
|
||
Задача Кузнецов Дифференциальные уравнения 3-20 |
|
|
||||
Условие задачи |
|
|
antiGTU |
|
|
|
|
|
|
|
|
|
|
Найти общий интеграл дифференциального уравнения. |
|
|
||||
|
Скачано |
с |
|
|
|
|
Решение |
|
|
|
|
||
|
|
|
|
|
||
Данное уравнение подходящей заме ой координат может быть сведено к однородному уравнению.
Найдем точку пересече ия прямых |
|
и |
. Для этого необходимо |
решить систему линейных лгебр ических уравнений: |
|
||
Выразим из первого ур внения и подставим во второе уравнение системы: |
|||
Как видим, решением системы будут |
, |
. Сделаем замену |
. |
Геометрический смысл данной замены состоит в том, что мы переносим начало координат в точку

, и уравнения данных прямых в этой системе не имеют свободных членов. Тогда |
, |
||||||||
, |
, |
и уравнение примет вид: |
. |
ru |
|
||||
|
|
||||||||
|
|
; |
|
|
antiGTU |
|
|
||
|
|
|
|
|
|
|
|||
|
; |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
В последнем уравнении вынесем из числителя и знаменателя |
: |
|
|
|
|||||
|
; |
|
|
|
|
|
|
|
|
Поскольку удалось записать уравнение |
в виде |
|
, то данное уравнение — |
|
|||||
|
|
|
с |
|
|
|
|
|
|
однородное дифференциальное уравнение. Оно может быть сведено к уравнению с |
|
|
|||||||
разделяющимися переменными если делать замену |
, где |
— новая неизвестная |
|
||||||
Скачано |
|
можем переписать как |
|
|
|
||||
функция. Тогда |
|
и уравнение |
|
|
|
||||
Выразим из данного урав е ия |
: |
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
 ;
;
 ;
;
 ;
;

 .
.
Разделим переменные в полученном уравнении. Для этого умножим обе части равенства на
. Заметим также, что |
|
. Имеем: |
. |
ru |
. |
|
|
||
|
|
|
|
|
Проинтегрируем обе части равенства: |
|
|
|
|
Интеграл в правой части равенства является табличным, и равен |
. В левой части равенства |
|||
|
antiGTU |
|
|
|
стоит интеграл от рациональной функции. Представим подынтегральную функцию в виде суммы простейших дробей:
 .
.
Сумму в правой части равенства приведем к общему знаменателю, и приравняем числители дробей в полученном равенстве:
 .
.
|
|
|
; |
с |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
При |
получаем |
. При |
|
: |
— откуда находим |
. |
Следовательно, |
|
|
|
|
|
|
, |
|
|
|
|
|
|
где |
— произвольн я постоянная. Таким образом, из |
вытекает равенство |
|
|||
|
Скачано |
|
|
|
|
|

Возвращаясь к |
согласно замене |
|
|
|
. |
ru |
и по |
, а затем переходя от , к переменным |
|
||||||
формулам |
, |
получим |
|
antiGTU |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
; |
|
|
|
|
. |
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
В последних равенствах использовались свойства логарифмов. |
|
|
|
||||
Ответ: Общий интеграл имеет вид |
|
|
где — произвольная |
||||
Скачано |
|
|
|
|
|
|
|
постоянная. |
|
|
|
|
|
|
|
Задача Кузнецов Дифференциальные уравнения 4-20 Условие задачи
Найти решение задачи Коши.
Решение
Данное уравнение является линейным дифференциальным уравнением первого порядка. Будем
искать неизвестную функцию в виде |
где |
, |
— новые неизвестные |
|
функции. Тогда |
. Подставляя данную замену в исходное уравнение получим |
|||
 ;
;

Найдем функцию |
из условия |
|
: |
|
|
ru |
|
|
; |
|
|
|
|
. |
|
||
|
|
|
|
|
|
|||
. |
|
|
antiGTU |
|
|
|||
; |
|
|
|
|
|
|||
Проинтегрировав обе части равенства находим |
— произвольная |
|||||||
|
, где |
|||||||
постоянная. Поскольку в качестве |
мы ищем любую функцию, для которой |
|
|
|
||||
можем положить |
. Тогда выразив получаем |
|
|
|
|
|||
. |
|
|
|
|
|
|
|
|
Подставим найденную функцию в |
. С учетом того, что |
|
получаем: |
|
||||
|
. |
|
|
|
|
|
|
|
Выразим из последнего равенства |
и проинтегрируем обе части равенства: |
|
|
|
||||
; |
|
с |
|
|
|
|
|
|
|
. |
|
|
|
|
|
||
Скачано |
|
|
|
|
|
, |
||
Применим к полученному интегралу формулу интегрирования по частям, где |
|
|||||||
, |
, |
: |
|
|
|
|
|
|
произвольная постоянная. |
|
|
|
|
|
, где |
||
|
|
|
|
|
|
|||
Таким образом, получили общее решение уравнения |
|
|
|
|
||||
|
|
|
|
. |
|
|
|
|
Из общего решения найдем функцию, удовлетворяющую условию |
|
: |
|
|
||||
|
; |
|
|
|
|
|
|
|
 ;
;
 .
.
ледовательно, решением задачи Коши является функция 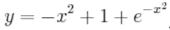
то
 —
—

Задача Кузнецов Дифференциальные уравнения 5-20 Условие задачи
Решить задачу Коши. |
|
|
antiGTU |
|
. |
ru |
|
|||
|
|
|
|
|
||||||
|
. |
|
|
|
|
|
|
|||
Решение |
|
|
|
|
|
|
|
|
||
Разделим обе части уравнения |
на |
. Получим уравнение |
|
|
|
|
|
|||
|
|
или |
|
|
|
|
|
|
|
|
Уравнение |
представляет собой неоднородное дифференциальное уравнение с постоянными |
|||||||||
коэффициентами. Общее решение уравнения |
будем искать в виде |
|
|
, где |
||||||
является общим решением соответствующего однородного уравнения, а |
— частное решение |
|||||||||
уравнения |
. |
|
|
|
|
|
|
|
|
|
Найдём корни характеристического многочлена, соответствующего уравнению |
|
|
: |
|||||||
|
; |
|
|
|
|
|
|
|
|
|
|
Скачано |
|
|
|
|
|
|
, где |
||
Следовательно, общим решением однородного уравнения является функция |
|
|
|
|||||||
— произвольная постоянная. Частн е решениес |
уравнения |
будем искать в виде |
|
|||||||
|
|
. Т гда |
|
|
. Подставляя |
и |
|
в уравнение |
||
|
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
Приравнивая в |
коэффициенты при одинаковых функциях в обеих частях равенства, получаем |
|||||||||
систему линейных алгебраи еских уравнений для нахождения |
и : |
|
|
|
|
|||||
Решением данной системы являются |
, |
, и частное решение уравнения |
имеет |
|||||||
вид |
|
. |
|
|
|
|
|
|
|
|
