20. Дайте определение арккосинуса числа. Приведите примеры.

Арккосинус числа х (arccos(x))- это такой угол из промежутка , косинус которого равен .

21. Дайте определение функции y=arccosx.

у = arccos (x)-это функция, обратная к функции у = cos (x) на .

22. Перечислите основные свойства функции y=arccosx.

Свойства функции:

1. D(arccos x)= .

2. E(arccos x)= .

3. у = arccos (x)-является функцией общего вида ( в отличае, от у = cos (x)).

arccos (-x)= - arccos (x)

4. Функция у=arccos (x)-является строго убывающей.

5. cos (arccos x)=x ; ;

arccos (cos (y))=y, .

6. Нуль функции. При у=0 ,х=1 так как arccosx=0

arccos x + arcsin x= .

23. Покажите как строится график функции y=arccosx.

Пусть На этом отрезке у = cos(x) строго монотонно возрастает и пробегает все значения из области значений синуса только один раз, значит, для функции у = cos(x) на отрезке существует обратная, которая обозначается у=arccos(x), график которой симметричен графику функции у = cos (x) на отрезке относительно прямой у=х.

24. Дайте определение арктангенса числа. Приведите примеры.

Арктангенсом числа х (arctg(x))- это такой угол из промежутка , тангенс которого равен .

25. Дайте определение функции y=arctgx.

у = arctg (x)-это функция, обратная к функции у = tg(x) на .

26. Перечислите основные свойства функции y=arctgx.

Свойства функции:

1. D(arctg x)= .

2. E(arctg x)= .

3. у = arctg (x) - нечетная функция ( как и у = tg (x)).

arctg (-x)= - arctg (x)

4. Функция у=arctg (x) - является строго возрастающая.

5. tg (arctg x)=x ; ;

arctg (tg (y))=y, .

6. Нуль функции. При у=0 ,х=0 так как arctgx=0

27. Покажите как строится график функции y=arctgx.

Пусть . На этом отрезке у = tg(x) строго монотонно возрастает и пробегает все значения из области значений тангенса только один раз, значит, для функции у = tg(x) на существует обратная, которая обозначается у = arctg(x), график которой симметричен графику функции у = tg (x) на отрезке относительно прямой у=х.

28. Дайте определение котангенса числа.

Арккотангенсом числа х (arcсtg(x))- это такой угол из промежутка , котангенс которого равен .

29. Дайте определение функции y=arcctgx .

у = arсctg (x)-это функция, обратная к функции у =сtg(x) на

30. Перечислите основные свойства функции y=arcctgx.

Свойства функции:

1. D(arсctg x)= .

2. E(arсctg x)= .

3. у = arсctg (x) – функция общего вида ( в отличае у = сtg (x)).

arcсtg (-x)= -arcсtg (x).

4. Функция у=arсctg (x) - является строго убывающая.

5. сtg (arcсtg x)=x ; ;

arcсtg (сtg (y))=y, .

6. Нуль функции. Не существует. Так как E(arсctg x)= .

31. Покажите как строится график функции y=arcctgx.

Пусть . На этом отрезке у = ctg(x) строго монотонно возрастает и пробегает все значения из области значений котангенса только один раз, значит, для функции у = сtg(x) на существует обратная, которая обозначается у = arcсtg(x), график которой симметричен графику функции у =сtg (x) на отрезке относительно прямой у=х.

33. Покажите с помощью тригонометрического круга частные случаи решения тригонометрических уравнений типа sinx = 0 sinx = 1 sinx = -1 cosx =0 cosx =1 cosx =-1

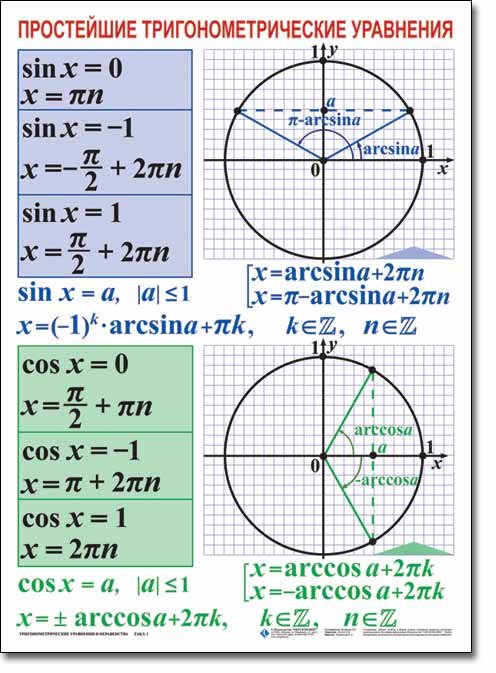
34. Выведите формулу корней тригонометрического уравнения sinx = a .

1. Строим единичную окружность в прямоугольной системе координат.

2. проводим прямую через точку у=а параллельную оси ОХ.

3. точки пересечения с окружностью являются решениями, а также все точки полученные при помощи полного оборота.

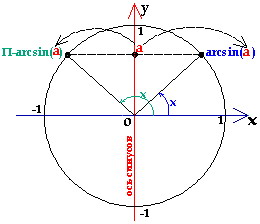
Общая формула: ,где  .

35. Выведите формулу корней тригонометрического уравнения cosx = a .

1. Строим единичную окружность в прямоугольной системе координат.

2. проводим прямую x=а параллельную оси ОY.

3. точки пересечения с окружностью являются решениями, а также все точки полученные при помощи полного оборота.

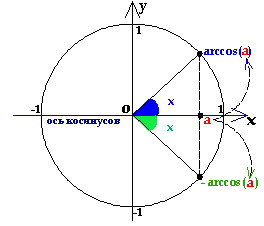
Общая формула: ,где  .

36. Выведите формулу корней тригонометрического уравнения tgx = a.

1. Строим график функции y=arctgx в прямоугольной системе координат.

2. проводим прямую y=а параллельную оси ОX.

3. точки пересечения с графиком являются решениями.

Общая формула: ,где 

37. Выведите формулу корней тригонометрического уравнения tgx = a.

1. Строим график функции y=arcсtgx в прямоугольной системе координат.

2. проводим прямую y=а параллельную оси ОX.

3. точки пересечения с графиком являются решениями.

Общая формула:, ,где  .