Комплексные числа
Всякое комплексное число z=a+bi≠0 единственным образом записывается в виде
z=r(cosφ+i sinφ),
где r – положительное число, равное модулю z, под знаком косинуса и синуса стоит один и тот же угол φ, равный аргументу z, при этом между косинусом и синусом стоит знак плюс. Эта запись называется тригонометрической формой числа z.
Пример. Представить в тригонометрической форме следующие комплексные числа:
а)
z1=-
-i,
в)
z2=-2+3i,
с)
z3=(-3)(cos
+i
sin
).
Решение.
а) z1=-
-i.
Найдем модуль |z
|=
=2.
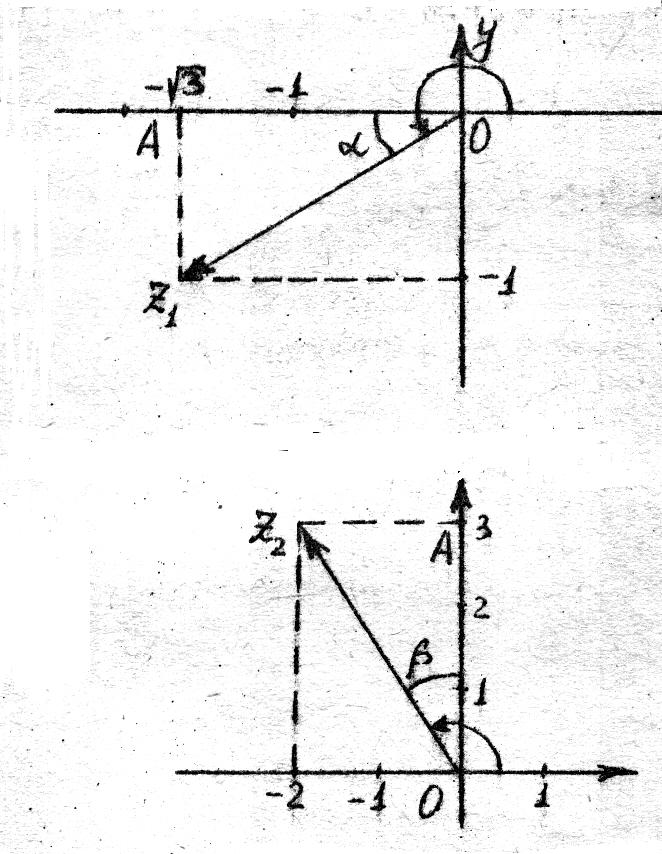
Изобразим число z1
на плоскости и найдем его аргумент. Из
чертежа видно arg z1=π+α.
Найдем угол α из треугольника z1AO.
Длины его сторон известны. Поэтому sin
α=
.
Отсюда α=
и
.
Тогда z1=
.
в)
z2=-2+3i,
|z2|=
,
arg z2=
β.
Из
треугольника
OAZ2
имеем
tg β=
и
β=arctg
.
О
ткуда
.
с)
.
Сравнивая тригонометрическую форму
числа с данным представлением числа
z3,
видим, что угол φ=arg z3
находится из условий
,
.
По формулам приведения получаем
,
,
следовательно,
.
Итак,
.
Пример.
Вычислить
.
Решение. Представим число под знаком корня в тригонометрической форме. Для этого представим в этой форме каждое комплексное число и выполним указанные действия.
.
Из формулы корня n-ой степени из комплексного числа
,
Отсюда,
полагая
,
получим
,
,
.
Пример. Найти множество точек z комплексной плоскости, удовлетворяющих условию
а)
|z-1+i|5 в)
а) Обратим внимание на геометрический смысл модуля разности z1-z2 комплексных чисел z1 и z2. Из геометрического истолкования вычитания комплексных чисел вытекает, что модуль разности z1-z2 есть не что иное, как расстояние между точками z1 и z2, изображающими эти числа на плоскости.
Отсюда следует, что множество точек z комплексной плоскости, для которых
|z-1+i|5 есть круг радиуса 5, с центром в точке (1,-1).
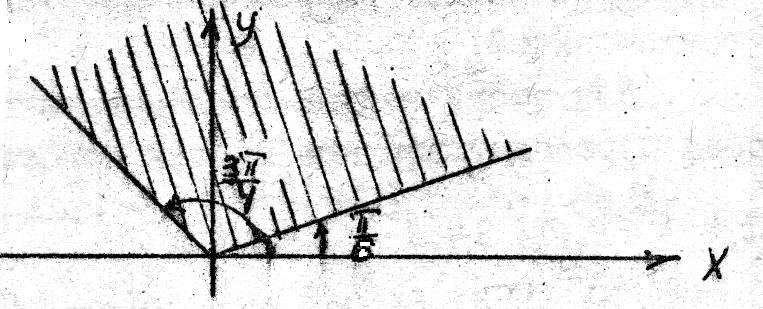
в) . Из определения аргумента комплексного числа получаем, что искомое множество имеет вид изображений на чертеже.
С помощью формулы Муавра можно получить выражение косинуса и синуса кратного угла nφ через косинус и синус простого угла φ.
Пример. Выразить sin3x и cos3x через sinx и cosx.
Решение. Рассмотрим комплексное число z=cosx+isinx. Возведем это число в третью степень дважды: один раз по формуле Муавра; второй раз – по биному Ньютона.
z3=cos3x+isin3x
Из равенства комплексных чисел следует:
,
По этой теме рекомендуем решить следующие задачи:
№ 101-109, 112, 113, 118-124, 136-139, 143-148 [6]
Подстановки и определители
Умение вычислять определители необходимо для решения многих задач линейной алгебры и аналитической геометрии.
Пример.
Определить характер четности подстановок
и
с
помощью разложения этих подстановок в
произведение транспозиций, если
,
.
Найти произведение
.
Решение. Найдем разложение подстановки в произведение транспозиций.
Для этого найдем последовательность транспозиций, которая переводит верхнюю строку подстановки в нижнюю:
.
Тогда
.
Аналогично,
.
Обе подстановки
и
разлагаются в произведение нечетного
числа транспозиций и поэтому являются
нечетными.
Вычислим произведение . По определению
.
Таким образом
.
Пример. Вычислить определитель
с помощью разложения по двум строкам или столбцам.
Решение. Применим теорему Лапласа ко 2-ой и 4-ой строке определителя. Получим
Пример. Вычислить определитель
Решение. С помощью элементарных преобразований, которые не меняют определитель, получим среди элементов определителя число 1 или –1. Для этого ко 2-й строке прибавим четвертую, умноженную на число –1:
Над полученным определителем проделаем следующие преобразования. Прибавим к 1-й строке вторую, умноженную на число 5, прибавим к 3-ей строке вторую, умноженную на число –3 и к 4-й строке прибавим вторую, умноженную на число –2.
Получим:
Используя теперь теорему Лапласа разложим определитель по 1-ому столбцу:
.
Теперь можно либо воспользоваться правилом для вычисления определителя
3-его порядка, либо проделать действия аналогичные приведенным выше. Прибавим к 1-ой строке вторую, умноженную на число –1;
Получим:
Применим теперь разложение по 1-ому столбцу:
Исходный определитель равен числу –2.
Для более полного овладения навыками в вычислении определителей и умножения подстановок рекомендуем решить следующие задачи:
На тему “Перестановки и подстановки”:
№ 123-145, 169-176 [5], № 235-240 [6]
На тему “Определители”:
№ 188-205, 212, 213, 221, 225-229, 236-240, 257-269, 426-436 [5].