МИНИСТЕРСТВО НАРОДНОГО ОБРАЗОВАНИЯ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Механико-математический факультет

Кафедра высшей алгебры

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ РАБОТЫ ПО КУРСУ “АЛГЕБРА И ТЕОРИЯ ЧИСЕЛ”

для студентов-заочников специальности 01.01

Минск 1989

Составители: Ю.В.Тишин, кандидат физико-математических наук, доцент

А.Э.Жигота

Утверждено на Совете факультета

25 сентября 1989 г., протокол № 1

П Р Е Д И С Л О В И Е

По курсу “Алгебра и теория чисел” студент-заочник выполняет четыре контрольные работы.

Предлагаемые методические работы содержат 10 вариантов первой контрольной работы. Включенные в него упражнения являются тем минимумом, которым должен овладеть каждый студент по темам: системы линейных уравнений, комплексные числа, подстановки, матрицы, определители, основные алгебраические системы. Методические указания предназначены помочь студентам-заочникам в овладении навыками решения задач. Здесь собраны типовые задачи по всем основным темам, изучаемым во втором семестре по курсу “Алгебра и теория чисел”. Каждая задача снабжена подробным решением, которое может служить образцом при самостоятельном решении аналогичных задач. Приведенный здесь материал заведомо не является достаточным для овладения предметом.

Перед выполнением контрольных работ следует изучить соответствующие разделы из учебников [1,2], руководствуясь приведенной ниже программой.

В качестве дополнительной литературы рекомендуем воспользоваться учебниками [3,4]. При возникновении затруднений можно обратиться на кафедру высшей алгебры за письменной консультацией.

Необходимо строго придерживаться следующих правил:

1. Студент выполняет работы только своего варианта.

2. Контрольную работу следует выполнять в тетради, оставляя поля 3-4 см. для замечаний рецензента. Рекомендуется оставлять в тетради несколько чистых листов для исправлений и дополнений в соответствии с указаниями рецензента.

3. На обложке тетради студент указывает фамилию, имя, отчество, номер контрольной работы и номер варианта. В конце работы студент указывает использованную литературу, дату окончания работы и ставит свою подпись.

4. Перед решением задачи надо полностью выписать ее условие. Решение каждой задачи необходимо сопровождать подробными объяснениями и ссылками на формулы, теоремы и правила. Вычисления должны быть доведены до конечного числового результата. Ответы и выводы, полученные при решении задач, следует подчеркнуть.

5. После получения прорецензированной работы необходимо исправить все отмеченные ошибки и недочеты. Если работа не зачтена, то необходимо переделать те задачи, на которые указывает рецензент, а при отсутствии такого указания вся контрольная работа должна выполняться заново. Переделанная работа представляется на повторное рецензирование обязательно с незачтенной ранее работой и рецензией к ней. При этом на обложке должна быть указана фамилия рецензента.

6. Контрольная работа должна быть зачтена до сессии.

Работы, выполненные без соблюдения этих правил, к зачету не принимаются и возвращаются без рецензирования для переработки.

Начальной букве фамилии студента соответствуют номера задач для контрольной работы № 1 определенного варианта. Эти номера приведены в следующей таблице:

№ п/п	Начальная буква Фамилии	Вари- анты	Номера задач для контрольных работ
1 2 3 4 5 6 7 8 9 10	А, У, Ф,Ш Б,Я В,Г,Ю Д,Е,Ж,З,Э К К,Л,Н,О М,Х П,Р,Ц С Т,Ч,Щ	1 2 3 4 5 6 7 8 9 10	1, 11, 21, 31, 41, 51, 61, 71, 81, 91, 101, 111, 121, 131, 141 2, 12, 22, 32, 42, 52, 62, 72, 82, 92, 102, 112, 122, 132, 142 3, 13 23, 33, 43, 53, 63, 73, 83, 93, 103, 113, 123, 133, 143 4, 14, 24, 34, 44, 54, 64, 74, 84, 94, 104, 114, 124, 134, 144 5, 15, 25, 35, 45, 55, 65, 75, 85, 95, 105, 115, 125, 135, 145 6, 16, 26, 36, 46, 56, 66, 76, 86, 96, 106, 116, 126, 136, 146 7, 17, 27, 37, 47, 57, 67, 77, 87, 97, 107, 117, 127, 137, 147 8, 18, 28, 38, 48, 58, 68, 78, 88, 98, 108, 118, 128, 138, 148 9, 19, 29, 39, 49, 59, 69, 79, 89, 99, 109, 119, 129, 139, 149 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150

ПРОГРАММА КУРСА “АЛГЕБРА И ТЕОРИЯ ЧИСЕЛ”

1. Делимость целых чисел. Теорема о делении с остатком. Наибольший общий делитель. Его существование и единственность. Алгоритм Евклида. Представление наибольшего общего делителя в виде линейной комбинации. Взаимно простые числа. Критерий взаимной простоты. Свойства взаимно простых чисел. Наименьшее общее кратное.

2. Простые числа. Свойства простых чисел. Основная теорема арифметики. Решето Эратосфена.

3. Линейные диофантовы уравнения. Критерий разрешимости. Решение линейных диофантовых уравнений.

4. Система комплексных чисел. Геометрическое истолкование действий с комплексными числами. Извлечение корней из комплексных чисел. Корни из единиц.

5. Отображения множеств.

6. Перестановки и подстановки.

7. Определители n-го порядка. Миноры и их алгебраические дополнения. Теорема Лапласа. Разложение определителя по элементам строки (столбца).

8. Системы линейных уравнений и их решение методом последовательного исключения неизвестных (метод Гаусса).

9. Операции над матрицами. Определитель произведения квадратных матриц. Обратная матрица. Правило Крамера.

10. Алгебраическая операция. Группы. Числовые кольца и поля.

ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ ТЕОРИИ ДЕЛИМОСТИ

Множество всех целых чисел будем обозначать Z,

Z = {..., -2,-1,0,1,2, ... }.

Сумма, разность и произведение двух чисел a,bZ также являются целыми числами, на частное может быть как целым, так и не целым числом.

В случае, когда частное от деления числа a на число b является целым (обозначим его q ), имеем или a = bq.В этом случае говорят, что a делится на b , или b делит a. Число b называется делителем a, число a – кратным b. Утверждение, что b делит a, будем кратко записывать так: b|a, если же b не делит a, то будем писать b ł a.

В общем случае, включающем и частный, когда a делится на b, справедлива следующая теорема.

Теорема о делении с остатком. Пусть a,b  Z, b ≠ 0. Тогда существует единственное представление числа a в виде a = bq + r, где q,r  Z, 0  r < |b|. Число q называется неполным частным, число r – остатком от деления a на b.

Заметим, что r = 0 тогда и только тогда, когда b|a .

Примеры. 1) a = 23, b = 5; 23 = 5·4 + 3;

2) a = -37, b = 8; -37 = 8·(-5) + 3;

3) a = -93, b = -7; -93 = -7·14 + 5;

4) a = 47, b = -12; 47 = (-12) · (-3) + 11.

Упражнения

1. Доказать, что произведение любых трех последовательных чисел делится на 6.

2. Доказать, что для любого целого n:

а) n³ - n делится на 3;

в) n⁵ - n делится на 5;

с) n⁷ - n делится на 7.

3. Показать, что если целое число n не делится на 7, то n³ – 1 или n³ + 1 делится на 7.

НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ (Н.О.Д.)

Пусть a₁, a₂, ..., a_n – целые числа не все равные нулю. Всякое целое d, которое делит каждое a_i, называется их общим делителем . Будем рассматривать только положительные общие делители. Общий делитель чисел a₁, a₂, ..., a_n , делящийся на любой другой общий делитель этих чисел, называется наибольшим общим делителем и обозначается символом (a₁, a₂, ..., a_n).

Для разыскания н.о.д. двух чисел применяется алгоритм Евклида, который состоит в следующем. Если a и b – натуральные числа и a > b, то

а = bq₁ + r₁, где 0 < r₁ < |b| ,

b = r₁q₂ + r₂, где 0 < r₂ < r₁ ,

r₁ = r₂q₃ + r₃, где 0 < r₃ < r₂ ,

....................................

r_n-2 = r_n-1q_n + r_n, где 0 < r_n < r_n-1 ,

r_n-1 = r_nq_n+1 + 0, где r_n+1 = 0 .

Последний отличный от нуля остаток r_n равен н.о.д. чисел a и b , т.е. (a,b) = r_n. Задача нахождения н.о.д. нескольких чисел сводится к аналогичной задаче для двух чисел с помощью формулы (a₁, a₂, ..., a_n )=(( a₁, a₂, ..., a_n-1),a_n). Поэтому сначала находится d₂=(a₁,a₂), затем d₃=(a₁,a₂,a₃)=(d₂,a₃),d₄=(a₁,a₂,a₃,a₄)=(d₃,a₄),...,d_n=( a₁, a₂, ..., a_n)=(d_n-1,d_n).

Если d=( a₁, a₂, ..., a_n) , то d можно представить в виде

d=u₁a₁+u₂a₂+...+u_na_n (I)

где u_iZ.

Отыскание чисел u_i,i= основано на использовании алгоритма Евклида. Покажем это на примере.

Пример. Найти н.о.д. (525,231,363) и представить его в виде (I).

Решение. С помощью алогритма Евклида найдем (525,231).

525=231 2+63 63=42 1 + 21

231=63 3 +42 42=21 2 (2)

Так как последний отличный от нуля остаток равен 21, то (525,231)=21

Найдем (525,231,363)=(21,363)

363=21·17+6

21=6·3+3 (3)

6=3·2

Следовательно, (21,363)=3. Тогда (525,231,363)=3. Представим число 3 в виде линейной комбинации чисел 21 и 363. Для этого из второго равенства (3) получим 3=21-6·3. Из первого равенства (3) получим 6=363-21·17. Отсюда

3=21- (363-21·17)·3=21·52+363·(-3). (4)

Теперь представим 21 в виде линейной комбинации чисел 525 и 231. Для этого из третьего равенства (2) получим 21=63-42. Из второго равенства (2) 42=231-63·3. Отсюда 21=63-(231-63·3)=63·4-231. Из первого равенства (2) 63=525-231·2. Поэтому

21=(525-231·2)·4-231=525·4+231·(-9). (5)

Наконец, подставляя выражение для 21 из (5) в (4), получим

3=(525·4+231·(-9))·52+363·(-3)=525·208+231·(-468)+363·(-3), т.е.u₁=208,

u₂=-468, u₃=-3 в формуле (I).

Наименьшее общее кратное

Пусть a₁, a₂, ..., a_n – отличные от нуля целые числа. Число, которое делится на каждое из этих чисел называется общим кратным этих чисел. Положительное общее кратное (2) называется наименьшим общим кратным (н.о.к.).

Н.о.к. чисел a₁, a₂, ..., a_n будем обозначать [a₁, a₂, ..., a_n].

Справедливы теоремы:

1. [a,b]= ;

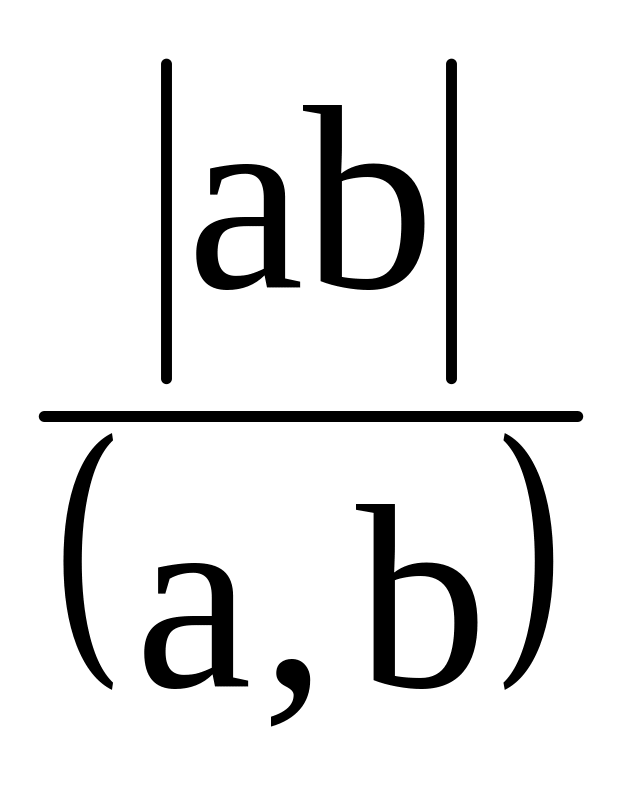2. [a₁, a₂, ..., a_n-1,a_n] = [[a₁, a₂, ...,a_n-1 ], a_n].