3.3. Признак оптимальности опорного плана. Снова рассмотрим линейную оптимизационную модель в предпочтительном виде:

, , ;

, j = .

Пусть эта задача решается на максимум. Начальный опорный план , значение целевой функции: .

Если для всех j , то целевая функция достигает максимума и − оптимальный план. Предположим, что существуют отрицательные значения . Пусть их несколько. Тогда выбираем наибольшее по модулю, из отрицательных , которое обозначим . Столбец назовем разрешающим. Соответствующую переменную введем в базис. Выбирая переменную, вводимую в базис (или выбирая разрешающий столбец) по наименьшему отрицательному элементу индексной - строки, обеспечивается не убывание целевой функции.

Для определения переменной, подлежащей исключению из базиса, составляются отношения свободных членов к положительным элементам разрешающего столбца (такие отношения называются симплексными). Наименьшее симплексное отношение и определяет строку (разрешающую), содержащую исключаемую переменную. Выбор переменной, исключаемой из базиса, но min симплексному отношению гарантирует положительность базисных компонент в новом опорном плане.

Значение новой базисной переменной в новом опорном плане будет равно . Численные значения остальных базисных переменных в новом опорном плане и соответствующее значение функции цели находятся после того, как измененная система базисных переменных будет выражена через измененную систему свободных переменных .

Установим правила, по которым осуществляется преобразование условий модели от одного базиса к другому. В каждом уравнении системы ограничений, где коэффициент при переменной , выделим слагаемое содержащее неизвестное :

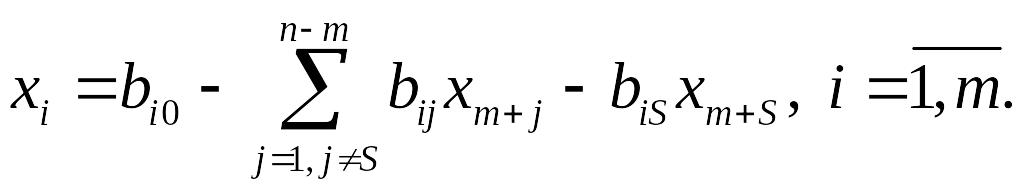
Затем - тое уравнение разрешаем относительно :

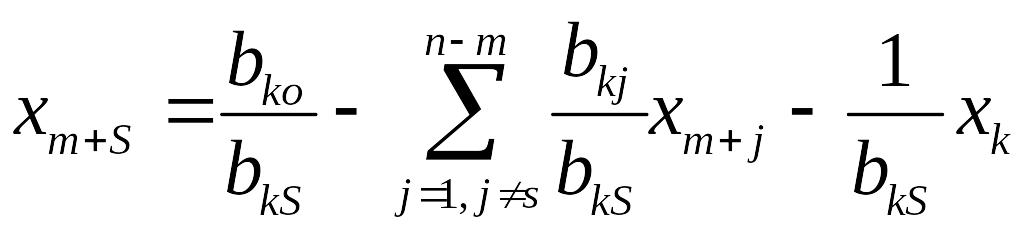(3.16)

и подставляем (3.16) во все остальные уравнения системы ограничений. Коэффициент при в уравнении (3.16) называют разрешающим элементом. В равенстве (3.16) новая базисная переменная выражена через свободные переменные, среди которых находится и бывшая базисная переменная .

Подставив (3.16) во все остальные уравнения системы ограничений, выражаем через новый набор свободных переменных остальные базисные переменные. Выполнив преобразования, получим:

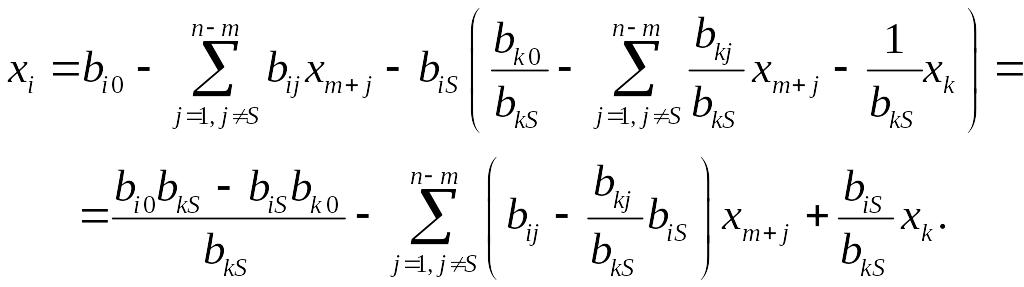(3.17)

Обозначив 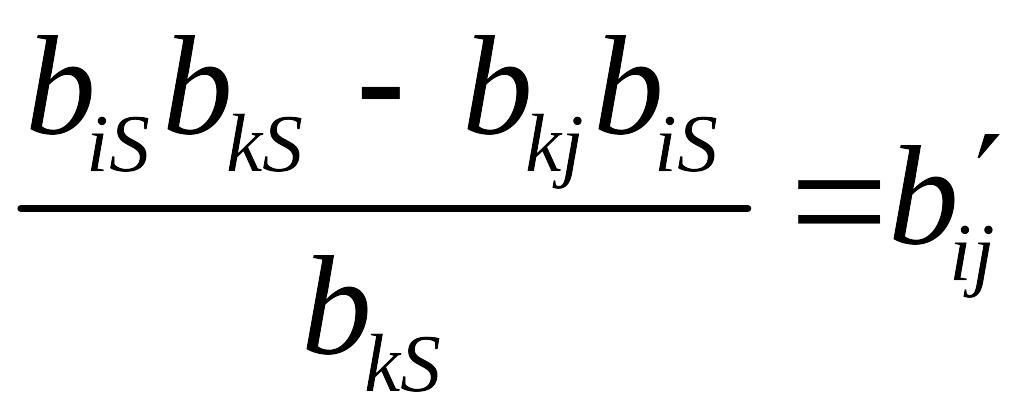, i = 0, 1, 2, …, m, i ≠ k; j = 0, 1, …, n – m, j ≠ s,

получим следующую систему равенств:

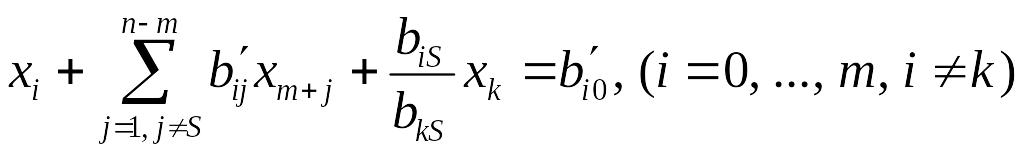. (3.18)

Приведение системы

, , ,

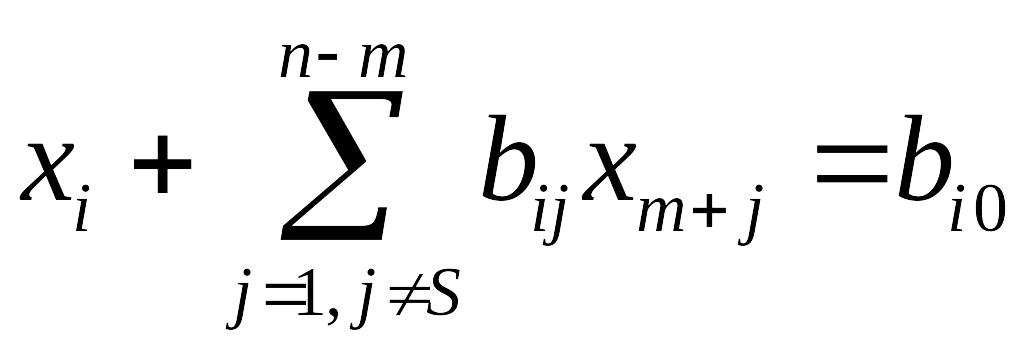к новому базису называется симплексным преобразованием. В результате получим симплексную таблицу 3.2:

Таблица 3.2

БП		СП
		… …
		… …
…	…	. . .
		… …
…	…	. . .
		… …
=		… …

Полагая в равенствах (3.16) и (3.18) свободные переменные равными нулю, получим компоненты нового опорного плана и новое значение целевой функции :

, .

Сформулируем правила перехода к новому опорному плану:

1. выбираем разрешающий элемент 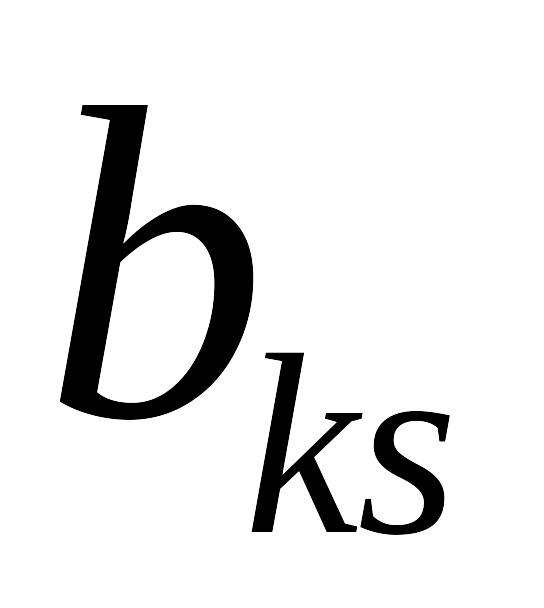, стоящий на пересечении разрешающей строки и разрешающего столбца;

2. разрешающий элемент заменяем обратной величиной ;

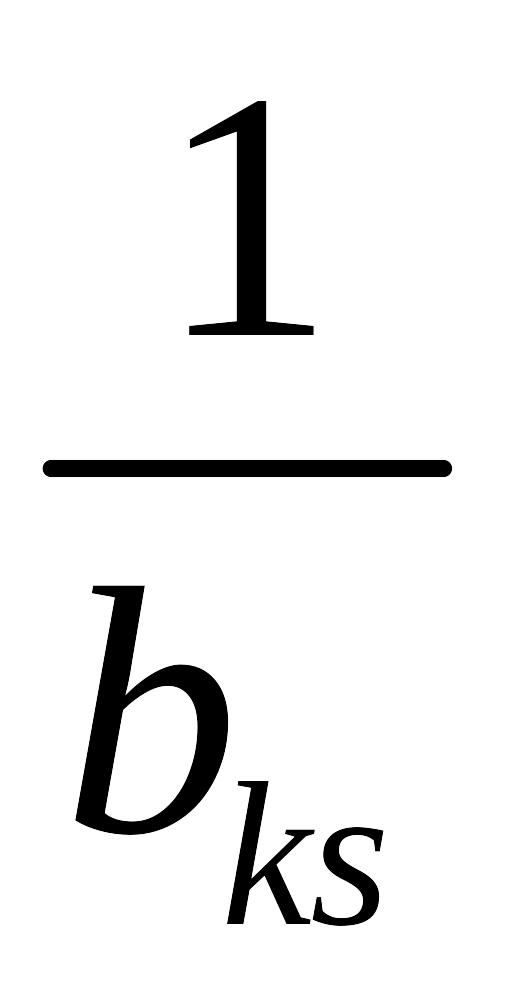3. остальные элементы разрешающей строки делим на разрешающий элемент : , ;

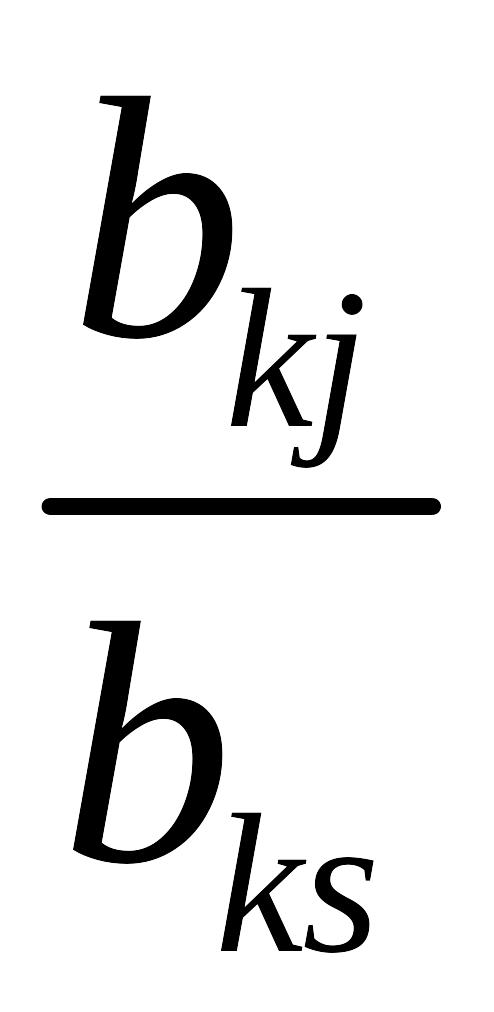4. остальные элементы разрешающего столбца делим на разрешающий элемент и меняем знаки;

5. все другие элементы симплексной таблицы вычисляются по правилу прямоугольника, вершинами которого служат разрешающий и преобразуемый элементы (они образуют главную диагональ) и два других элемента (они образуют побочную диагональ), составляющих прямоугольник: .

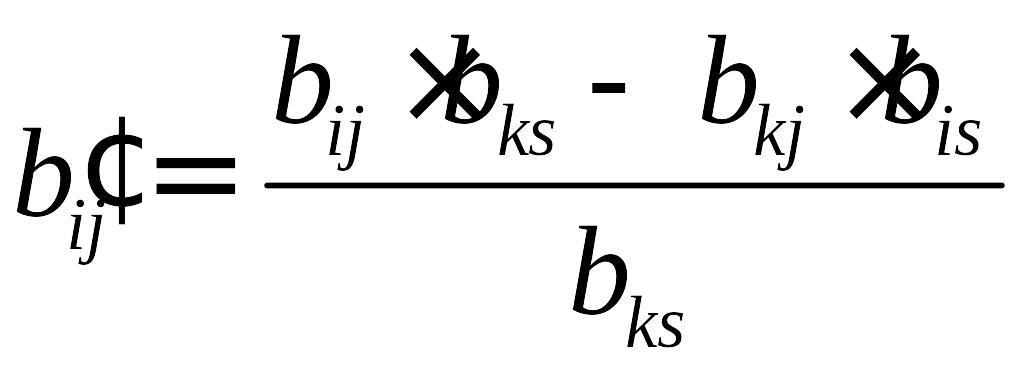Таким образом, симплекс-метод представляет собой процесс направленного решения системы линейных уравнений – ограничений задачи с особым правилом выбора разрешающего элемента, обеспечивающим движение по опорным решениям (правило выбора разрешающей строки) и монотонный рост линейной функции цели (правило выбора разрешающего столбца).

Сформулируем теоремы, в которых определяются условия оптимальности планов, бесконечности оптимальных планов, неограниченности целевой функции.

Теорема 3.1. Если для некоторого опорного плана, при решении модели на максимум, все элементы в индексной строке последней симплексной таблицы неотрицательны, то такой план оптимальный.

Теорема 3.2. Если для некоторого опорного плана, при решении модели на минимум, все элементы в индексной строке последней симплексной таблицы неположительны, то такой план оптимальный.

Теорема 3.3. Если в индексной строке последней симплексной таблицы, содержащей оптимальный план, имеется хотя бы один нулевой элемент, соответствующий свободной переменной, то линейная оптимизационная модель имеет бесконечное множество оптимальных планов; если же все элементы положительны, то оптимальный план единственный.

Теорема 3.4. Если в индексной строке симплексной таблицы, при решении модели на максимум, имеется отрицательный элемент, а в соответствующем столбце нет ни одного положительного элемента, то целевая функция не ограничена сверху на множестве допустимых планов.

Теорема 3.5. Если в индексной строке симплексной таблицы, при решении модели на минимум, имеется положительный элемент, а в соответствующем столбце нет ни одного положительного элемента, то целевая функция не ограничена снизу на множестве допустимых планов.

Пример 3.1. Предприятие может изготовлять четыре вида продукции П , П , П , П . Сбыт любого ее объема обеспечен. Предприятие располагает в течение квартала трудовыми ресурсами в 100 чел, полуфабрикатами массой 260кг, станочным оборудованием в 370 станко - смен. Нормы ресурсов и прибыль от единицы каждого вида продукции представлены в таблице 3.3:

Таблица 3.3

Ресурсы	Продукция				Объем ресурсов
	П	П	П	П
Трудовые ресурсы, чел.	2,5	2,5	2	1,5	100
Полуфабрикаты, кг	4	10	4	6	260
Станочное оборудование, станко-смен	8	7	4	10	370
Прибыль от единицы продукции, руб.	40	50	100	80	max

Необходимо:

1) определить план выпуска продукции, максимизирующий прибыль;

2) решить задачу с требованием комплектации, чтобы количество единиц третьей продукции было в 3 раза больше количества единиц первой;

3) выяснить оптимальный ассортимент при дополнительных ограничениях: первого продукта выпускать не менее 25 единиц, третьего – не более 30, второго и четвертого – в отношении 1 : 3.

Решение. Построим математическую модель задачи. Пусть , - неизвестные, характеризующие количество выпускаемой продукции предприятием. Требуется определить план , при котором предприятие получит максимум прибыли, т. е. целевая функция

.

План удовлетворяет ограничениям:

а) на трудовые ресурсы:

;

на полуфабрикаты:

;

на станочное оборудование:

;

условия неотрицательности:

, j = ;

б) дополнительное условие комплектации:

;

в) дополнительные условия:

.

Приведем вначале систему ограничений к предпочтительному виду, добавив к левым частям дополнительные переменные . Получим расширенную задачу, эквивалентную данной.

В расширенной задаче система ограничений

имеет предпочтительный вид. В целевую функцию дополнительные переменные вводятся с коэффициентами равными нулю: .

Заносим условия расширенной задачи в симплексную таблицу 3.4:

Таблица 3.4

БП	А	СП
	100	2,5	2,5		1,5
	260	4	10	4	6
	370	8	7	4	10
Функция	0	-40	-50	-100	-80

Рассчитаем элементы индексной строки:

– произведение вектора коэффициентов целевой функции, стоящих у базисных переменных = (0, 0, 0) и вектора свободных членов у системы ограничений в предпочтительном виде А = (100, 260, 370).

Так как - строка содержит 4 отрицательных элемента, то в базис будем вводить переменную , которая соответствует наименьшему значению , : = - 100. Разрешающим столбцом будет третий столбец.

Для определения переменной, подлежащей исключению из базиса, составляем отношения свободных членов к положительным элементам разрешающего столбца. В разрешающем столбце все элементы положительные: 100/2 =50; 260/4 = 65; 370/4 = 92,5. Выбираем наименьшее, которое определяет первую строку в качестве разрешающей.

Таким образом, разрешающим элементом будет «2». Строим новую симплексную таблицу 3.5:

Таблица 3.5

БП		СП
	50	1,25	1,25	1/2	0,75
	60	-1	5	-2
	170	3	2	-2	7
-строка	5000	85	75	50	-5

-строка содержит один отрицательный элемент, поэтому разрешающим столбцом будет четвертый, и в базис будет вводиться переменная .

Составляем отношения свободных членов к положительным элементам разрешающего столбца:

500/0,75 = 66; 60/3 = 20; 170/70 = 24.

Так как отношение 60/3 = 20 – наименьшее, то третья строка разрешающая. Разрешающий элемент «3». Строим новую симплексную таблицу 3.6:

Таблица 3.6

Б. П.	А	СП
	35
	20
	30
-строка	5100	250/3	250/3	140/3	5/3

Так как в - строке нет отрицательных элементов, то план

Х* = (0, 0, 35, 20, 0, 0, 30)

расширенной задачи - оптимальный. Задача имеет единственное решение:

(Х*) = 5100,

так как в - строке нет нулевых элементов.