
- •Часть I
- •Предисловие
- •Введение Экономико-математическое моделирование как средство для принятия эффективных решений
- •Оптимизационные модели
- •1.2. Примеры линейных оптимизационных моделей
- •2. Свойства решений линейных оптимизационных моделей
- •3. Симплексный метод
- •3.3. Признак оптимальности опорного плана. Снова рассмотрим линейную оптимизационную модель в предпочтительном виде:
- •4.Двойственность линейных оптимизационных моделей
- •4.1. Понятие двойственности. Построение двойственных моделей.
- •4.3. Теоремы двойственности. Рассмотрим пару взаимно двойственных моделей:
- •Тест № 1
- •1) Положительна;
- •5. Транспортные модели
- •5.2. Признак разрешимости транспортной модели.
- •Тест № 2
- •6. Модели теории игр
- •6.2. Модели матричных игр
- •Последовательно преобразуем первоначальную симплексную таблицу:
- •В последней симплексной таблице содержится оптимальный план: ; . Учитывая соответствие между переменными, находим оптимальный план игрока : ; .
- •6.3. Модели статистических игр
- •Тест № 3
- •7. Целочисленные оптимизационные модели
- •7.1. Формулировка целочисленной оптимизационной модели. Примеры. Методы решения
- •7.2. Алгоритм метода Гомори решения целочисленных оптимизационных моделей.
- •Литература
- •Экономико-математические методы и модели
- •Часть I
Оптимизационные модели
1.1. Общая формулировка оптимизационной модели. Оптимизационные модели представляют систему математических уравнений, линейных или нелинейных, подчиненных определенной целевой функции и служащих для отыскания наилучших (оптимальных) решений конкретной экономической задачи. Эти модели относятся к классу экстремальных задач и описывают условия функционирования экономической системы.
Оптимизационные модели могут носить детерминированный или стохастический характер. В детерминированных моделях результат решения однозначно зависит от входных данных. Стохастические модели описывают случайные процессы, в которых результат всегда остается неопределенным.
Наиболее разработаны и практически более применимы детерминированные модели, использующие аппарат математического программирования.
Структура оптимизационной модели состоит из целевой функции, принимающей значения в пределах ограниченной условиями задачи области, и из ограничений, характеризующих эти условия.
В общем виде оптимизационную математическую модель можно представить в следующем виде:
Найти план
![]() ,
который max (min)
целевую функцию
,
который max (min)
целевую функцию
![]() (1.1)
(1.1)
при выполнении ограничений
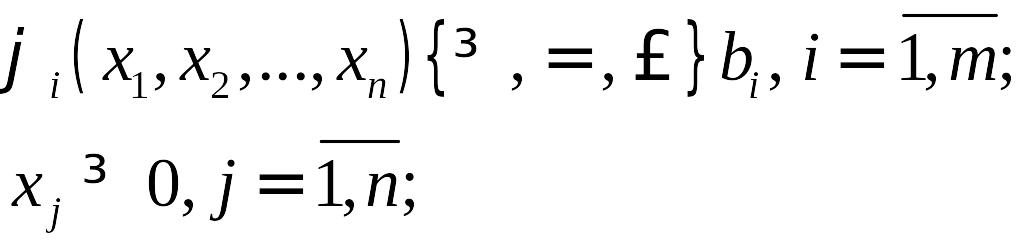 (1.2)
(1.2)
где
![]() и
и
![]() - известные функции,
- известные функции,
![]() - заданные постоянные величины.
- заданные постоянные величины.
Вид целевой
функции
![]() ,
вид ограничений и специальные ограничения
на переменные (например, требования
целочисленности переменных) определяют
выбор метода математического
программирования для решения
оптимизационной задачи:
,
вид ограничений и специальные ограничения
на переменные (например, требования
целочисленности переменных) определяют
выбор метода математического
программирования для решения
оптимизационной задачи:
линейного программирования;
нелинейного программирования;
динамического программирования;
целочисленного программирования и т. д.
Мы остановимся на оптимизационных моделях, которые решаются методами линейного программирования, т. е. рассмотрим оптимизационные модели (1.1) - (1.2) у которых целевая функция и ограничения - линейные функции. Тогда оптимизационная математическая модель примет вид:
Найти план , который max (min) целевую функцию
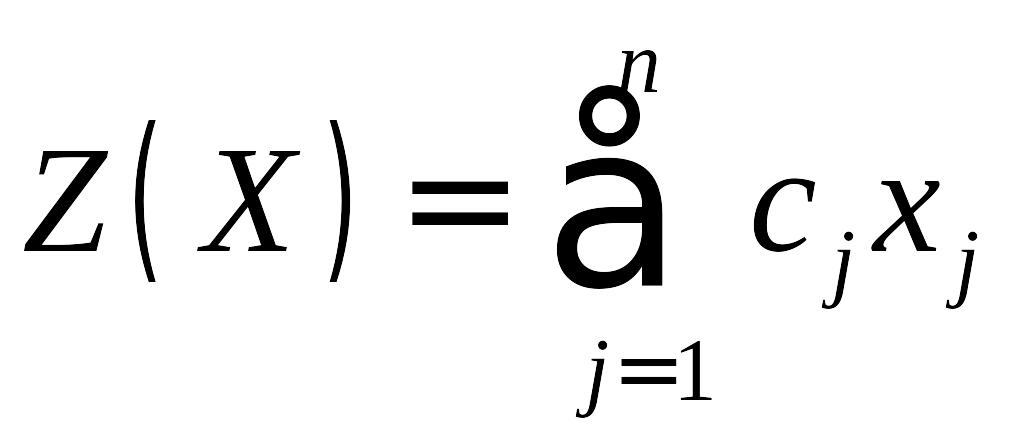 (1.3)
(1.3)
при выполнении системы ограничений
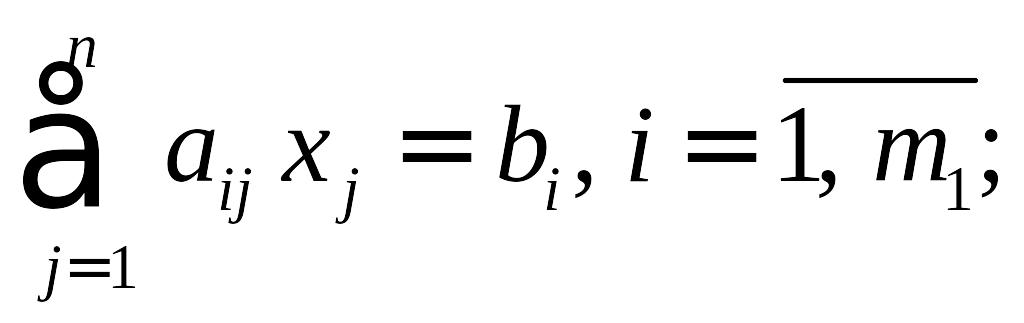 (1.4)
(1.4)
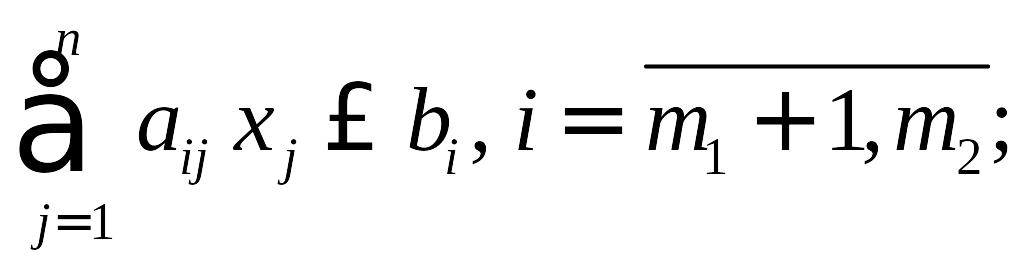 (1.5)
(1.5)
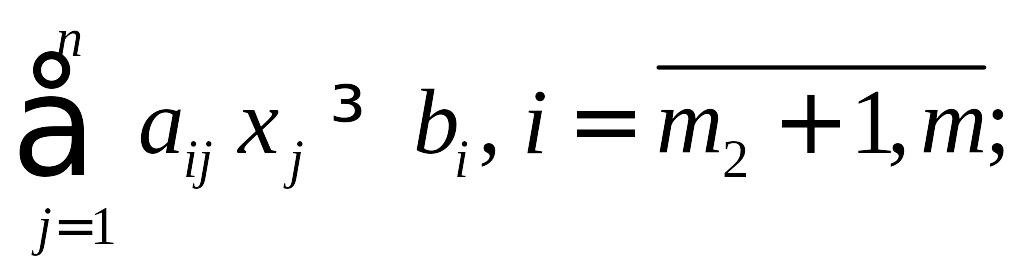 (1.6)
(1.6)
![]() (1.7)
(1.7)
Множество планов
![]() ,
удовлетворяющих системе ограничений
(1.4) – (1.7), называется множеством допустимых
решений и обозначается
,
удовлетворяющих системе ограничений
(1.4) – (1.7), называется множеством допустимых
решений и обозначается
![]() .
Допустимый план
.
Допустимый план
![]() ,
доставляющий целевой функции (1.3)
экстремальное значение, называется
оптимальным.
,
доставляющий целевой функции (1.3)
экстремальное значение, называется
оптимальным.
Отметим, что
максимизация целевой функции
![]() в области допустимых решений
эквивалентна задаче минимизации функции
«
в области допустимых решений
эквивалентна задаче минимизации функции
«![]() »
в той же области:
»
в той же области:
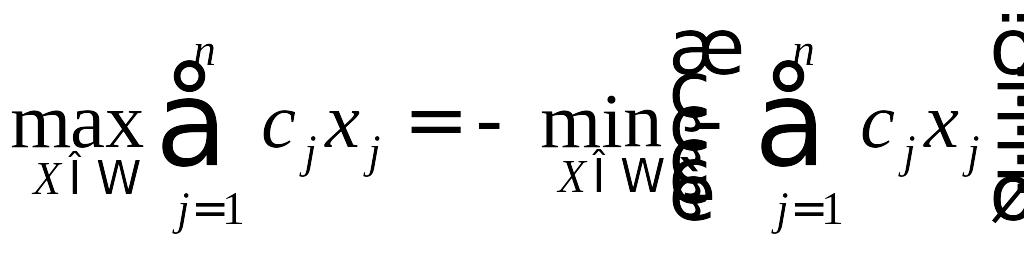 .
.
Если все
ограничения задачи заданы в виде равенств
и на все переменные
![]() ,
наложено условие неотрицательности
,
наложено условие неотрицательности
![]() ,
то оптимизационная модель имеет
каноническую форму записи:
,
то оптимизационная модель имеет
каноническую форму записи:
max
при ограничениях
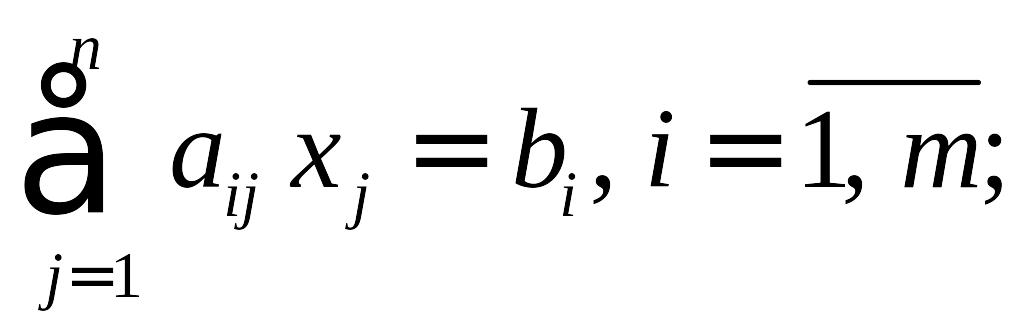
![]() .
.
Если ограничения заданы в виде неравенств, то оптимизационная модель имеет симметрическую форму записи:
max
при ограничениях
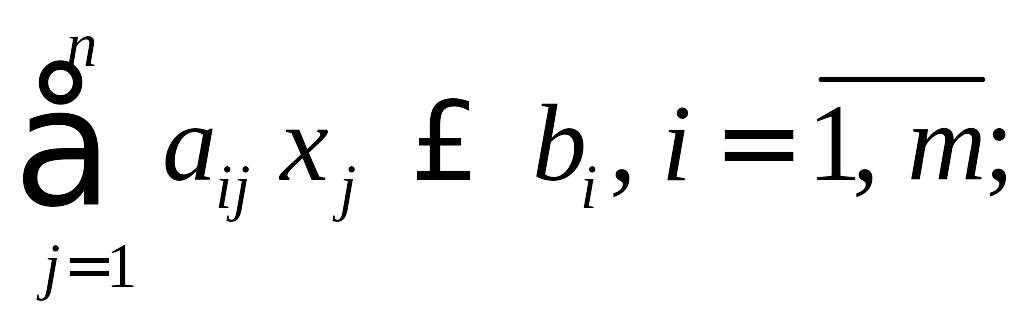
,
или
min
при ограничениях
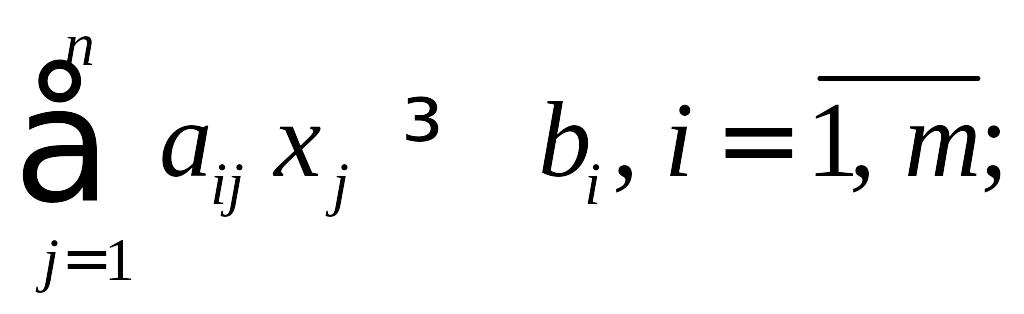
.
Для аналитического
решения линейной оптимизационной
модели, в случае необходимости, ее
ограничения следует преобразовать к
каноническому виду, для чего переходят
от ограничений неравенств к равенствам,
введением дополнительных переменных
![]() ,
которые прибавляют к левым частям
ограничений неравенств. В целевую
функцию дополнительные переменные
вводятся с коэффициентами равными нулю.
,
которые прибавляют к левым частям
ограничений неравенств. В целевую
функцию дополнительные переменные
вводятся с коэффициентами равными нулю.
