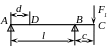4. Расчет на жесткость

Расчеты на жесткость выполняют по рекомендациям курса «Сопротивление материалов». В общем случае упругие деформации определяют, используя интеграл Мора и способ Верещагина. Расчетные формулы для простых случаев нагружения приведены в

Таблица 4.1

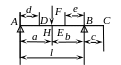
Углы наклона θ и прогибы y
θA
θB
θC	θB
θD
θE		-
θH		-
yD
yE		-
yH		-
yC	θB ·c

табл. 4.1. При выводе этих формул вал рассматривался как брус постоянного сечения приведенного диаметра [3,5].

Для валов зубчатых передач стрела прогиба y под колесом не должна превышать следующих величин:

цилиндрические передачи [y] ≤ 0,01 m;

конические и гипоидные передачи [y] ≤ 0,005 m;

где m – модуль зацепления;

в станках [y] = (0,0002…0,0003) l,

где l – расстояние между опорами.

Угол θ наклона упругой линии вала:

в подшипнике качения радиальном шариковом [θ] = 0,0005 рад;

в подшипнике скольжения [θ] = 0,001 рад.

5. Пример расчета

Выполнить расчет ведущего вала одноступенчатого цилиндрического косозубого редуктора по следующим данным: передаваемая валом мощность Р₁ = 9,5 кВт; угловая скорость ₁ = 100 рад/с; материал вала – сталь 45, термическая обработка – улучшение; эскиз вала показан на рис. 5.1.а. На валу установлена шестерня с делительным диаметром d₁ = 110 мм, ширина шестерни b₁= l_ст = 100 мм, угол наклона зубьев  = 10. К выходному концу вала приложена дополнительная нагрузка F_м от муфты.

Примечания: 1) Обозначенные на рис. 5.1.а буквами размеры обычно определяют при выполнении эскизного проекта [1,2]. Если эскизный проект еще не разработан, ориентировочно размеры могут быть определены непосредственно при выполнении расчета, как показано ниже [3,5].

2) При использовании электронного калькулятора для инженерных расчетов линейные размеры, не подлежащие округлению до стандартных значений, вычисляют с точностью до сотых долей миллиметра, результаты вычислений остальных величин обычно округляют до трех значащих цифр.

5.1. Определяем передаваемый валом момент Т₁:

Нм.

5.2. Внешние нагрузки, действующие на вал:

а) Силы в зацеплении, определенные при расчете зубчатой передачи:

окружная Н;

радиальная Н,

где α – угол зацепления, для зубчатых колес без смещения или равносмещенных α = 20

осевая F_а = F_t· tg  = 1730·tg 10 = 305 Н;

б) Нагрузка от муфты:

F_м = 50· = 50· = 487 Н.

5.3. По эскизу определяем расстояние l между точками приложения реакций в опорах:

l ≈ l_ст + a₁ + а₂ + В/2 + В/2 = 100 + 10 + 10 + 10 + 10 = 140 мм,

где a₁ и а₂ - расстояние между стенкой корпуса редуктора и торцом зубчатого ко- леса, для одноступенчатых редукторов a₁ = а₂= a = 5…10 мм; для двухступенчатых редукторов в размер а₂ включают также ширину колеса второй ступени и расстояние между торцами колес первой и второй ступеней, обычно равное а/2; в рассматриваемом случае принимаем a = 10 мм;

В – ширина подшипника качения, принимаем ориентировочно В ≈ 20 мм; после выбора подшипников размер B следует уточнить и при необходимости внести соответствующие изменения в размеры вала.

5.4. Расстояние l₃ от точки приложения силы F_м до левой опоры:

l₃ = l_м/2 + l_п – В/2 = 60/2 + 50 – 10 = 70 мм,

где l_м – длина посадочного участка под муфту, принимаем l_м = 60 мм;

l_п – длина участка вала под уплотнением и подшипником, принимаем l_п = 50 мм.

5.5. Составляем схему нагружения вала в двух взаимно перпендикулярных плоскостях – вертикальной Y и горизонтальной X .

Схема нагружения вала в прямоугольной системе координат показана на рис. 5.1,б. Линии x, y, и z пересечения координатных плоскостей X, Y, и Z называются координатными осями. Начало координат находится в общей точке О пересечения трех координатных осей. Оси x и y лежат в плоскости Z, ось z перпендикулярна плоскости Z. При расчете валов принято показывать только положение координатных осей, координатные плоскости не показывают.

Обычно вал располагают так, что его геометрическая ось совпадает с осью z, а действующие на вал силы раскладывают по направлениям, параллельным осям x и y. В этом случае передаваемый валом крутящий момент действует относительно оси z и обозначается M_z, в рассматриваемом примере M_z = М_к = T₁. Составляющие сил, действующие в плоскости X, создают изгибающие моменты относительно осей, параллельных координатной оси y, в обозначении этих изгибающих моментов принято ставить индекс y: M_y = М_и^Г; составляющие сил, действующие в плоскости Y, создают изгибающие моменты относительно осей, параллельных координатной оси x, соответственно в обозначение этих изгибающих моментов вводят индекс x: M_x = М_и^В.

При составлении схемы нагружения вала направление силы F_м выбирают так, чтобы она увеличивала напряжения и деформации от силы F_t [3].

5.6. По правилам, известным из курса «Сопротивление материалов», определяем опорные реакции и изгибающие моменты:

а) опорные реакции A_y и B_y в вертикальной плоскости (рис. 5.1,в):

;

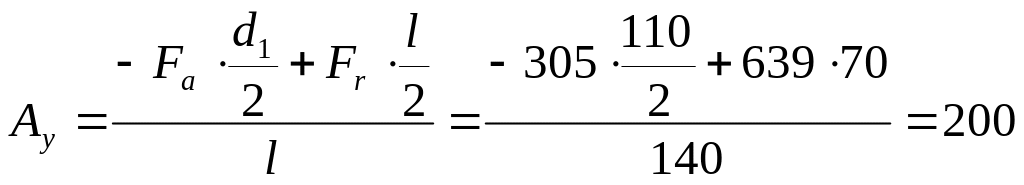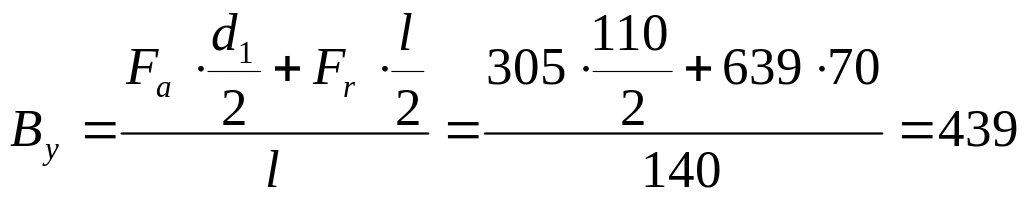Н;

;

Н;

б) изгибающие моменты M^_xI и M^_xI в вертикальной плоскости:

Н·мм,

Н·мм;

в) опорные реакции A_x и B_x в горизонтальной плоскости (рис. 5.1,г):

;

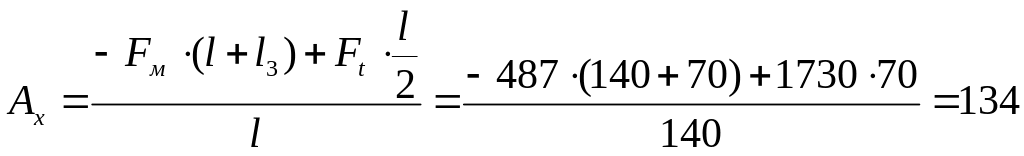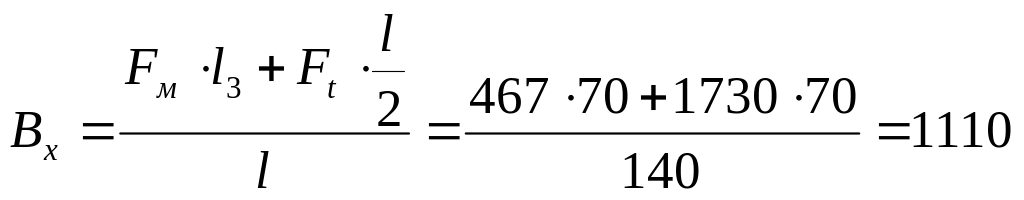Н;

;

Н;

г) изгибающие моменты M_yI и M_yII в горизонтальной плоскости:

Н·мм;

M_yII = F_м·l₃ = 487·70 = 34100 Н·мм.

5.7. Результирующий изгибающий момент M в сечении I-I:

Н·мм.

5.8. Реакции в опорах:

Н;

Н.

5.9. Если эскизный проект вала еще не выполнен, предварительно определяют средний диаметр d_ср вала из расчета только на кручение, приняв [τ]=12…15 МПа [3]:

мм.

Диаметр d_ш вала под шестерней получаем, округлив d_ср до ближайшего большего значения по ГОСТ 6636-69, окончательно принимаем d_ш= 36 мм.

5.10. Диаметр d_п под подшипниками должен быть меньше d_ш= 36 мм и в диапазоне размеров от 20 до 495 мм кратным 5, следовательно, d_п= 35 мм.

5.11. Диаметр участка вала под манжетным уплотнением принимаем равным d_п .

5.12. Диаметр d_в выходного конца вала должен быть меньше d_п на две высоты буртика t_ц = 3,5 мм, т.е. d_в= d_п – 2 · t_ц = 35 – 2 · 3,5 = 28 мм, что соответствует ГОСТ 12080-66 «Концы валов цилиндрические» [1, 2] .

5.13. Диаметр d_бш буртика должен быть больше диаметра d_ш на две высоты заплечиков t = 4,0 мм: d_бш= d_ш + 2 · t = 36 + 2 · 4 = 44 мм.

5.14. Механические характеристики стали 45 улучшенной при диаметре заготовки до 80 мм (табл. 2.1):

предел прочности σ_в = 900 МПа;

предел текучести σ_т = 650 МПа;

предел текучести при кручении τ_т = 390 МПа;

предел выносливости гладких образцов

при симметричном цикле изгиба σ_-1 = 410 МПа;

предел выносливости гладких образцов

при симметричном цикле кручения τ_-1 = 230 МПа;

коэффициент ψ_τ = 0,1.

5.15. Момент сопротивления W при изгибе для сечения с одним шпоночным пазом:

мм³,

где b – ширина шпонки, мм; по ГОСТ 12080-66 для диапазона размеров св.30 до 38 мм b = 10 мм;

h – высота шпонки, мм; по ГОСТ 12080-66 для диапазона размеров св.30 до 38 мм h = 8 мм.

5.16. Момент сопротивления W_к при кручении для сечения с одним шпоночным пазом:

мм³.

5.17. Нормальные напряжения σ_и = σ_а в сечении I-I :

МПа.

5.18. Касательные напряжения τ_к в сечении I-I :

МПа.

5.19. Вычисляем коэффициент K_σD снижения предела выносливости при изгибе:

,

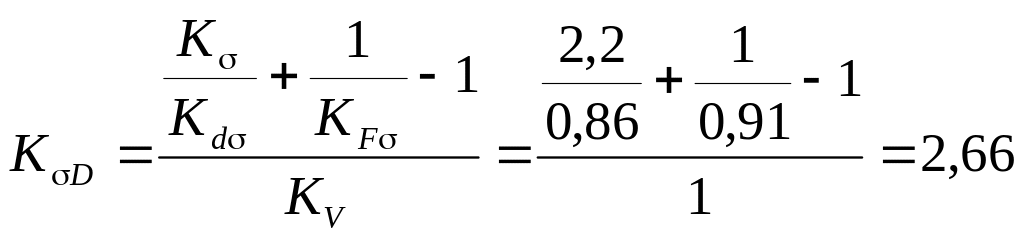где К_σ – эффективный коэффициент концентрации нормальных напряжений (табл. 3.2), К_σ = 2,2;

К_dσ – коэффициент влияния абсолютных размеров поперечного сечения (табл. 3.4), К_dσ = 0,86;

К_Fσ – коэффициент влияния качества поверхности (табл. 3.6), при R_a = 0,8 мкм К_Fσ = 0,91;

К_V – коэффициент влияния поверхностного упрочнения (табл. 3.7), К_V = 1,0.

5.20. Вычисляем коэффициент К_τD снижения предела выносливости при кручении:

,

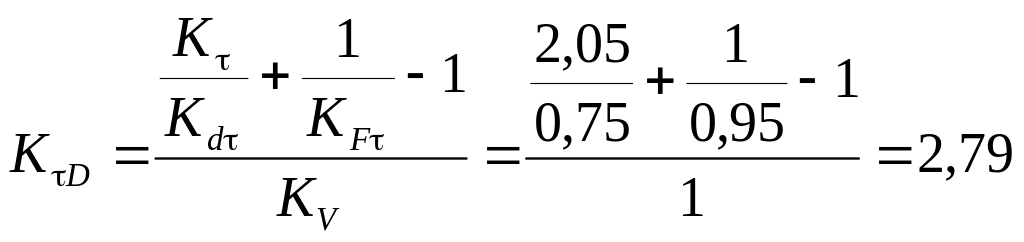где К_τ – эффективный коэффициент концентрации касательных напряжений (табл. 3.2), К_σ = 2,05;

К_dτ – коэффициент влияния абсолютных размеров поперечного сечения (табл. 3.4), К_dσ = 0,75;

К_Fτ – коэффициент влияния качества поверхности (табл. 3.6), при R_a = 0,8 мкм К_Fσ = 0,95.

5.21. Коэффициент влияния асимметрии цикла ψ_τD:

.

5.22. Пределы выносливости σ_-1D и τ_-1D для сечения I-I :

МПа;

МПа.

5.23. Коэффициент запаса прочности S_σ по нормальным напряжениям:

.

5.24. Коэффициент запаса прочности S_τ по касательным напряжениям:

.

5.25. Коэффициент S запаса прочности для сечения I-I :

.

5.26. Прочность вала в сечении I-I обеспечена, так как коэффициент S = 6,57 значительно превышает минимально допустимое значение [S] =1,5…2,5.

5.27. Определяем коэффициент S запаса прочности для сечения II-II (под левым подшипником качения): в этом сечении действует изгибающий момент M_II = 34100 Н·мм; момент сопротивления сечения при изгибе W = 4210 мм³, при кручении W_к = 8420 мм³; нормальные напряжения

МПа,

касательные напряжения

МПа;

коэффициенты снижения пределов выносливости

,

;

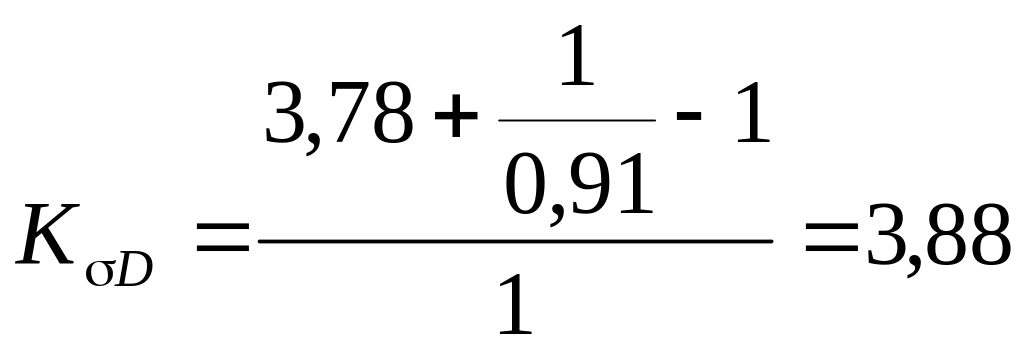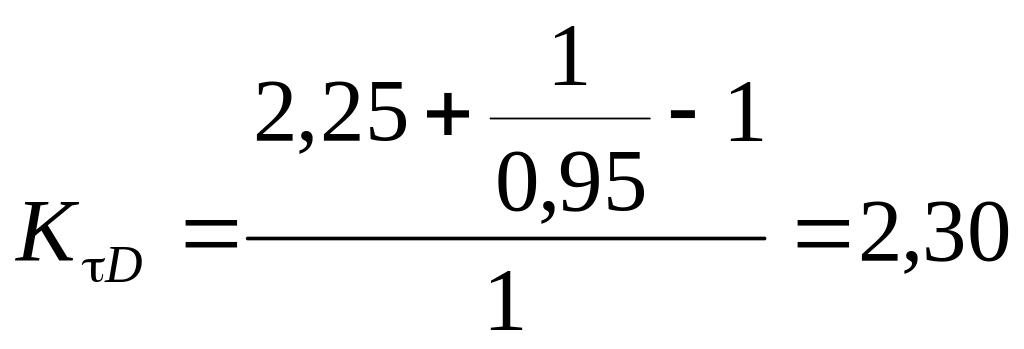коэффициент влияния асимметрии цикла

;

пределы выносливости

МПа,

МПа;

коэффициенты запаса прочности по нормальным и касательным напряжениям

,

;

коэффициент запаса прочности

,

полученная величина также значительно превышает минимально допустимое значение [S] =1,5…2,5, следовательно, прочность вала в сечении II-II обеспечена.

5.28. Проверяем статическую прочность вала.

Для двигателя АИР160S6 отношение максимального вращающего момента к номинальному T_max/T = 2,5 [1,табл. 24.9], следовательно, К_п = 2,5.

Нормальные напряжения σ в сечении I-I :

МПа,

где M_max – наибольший суммарный изгибающий момент

Н·мм;

F_max – наибольшая осевая сила

F_max = K_п·F_a = 2,5 · 305 =762 Н;

A – площадь поперечного сечения вала

мм².

Касательные напряжения τ в сечении I-I :

МПа,

где T_кmax – наибольший крутящий момент,

T_кmax = 10³ ·K_п · Т₁ = 10³ · 2,5 · 95 = 237500 Н·мм.

Коэффициент S_Tσ запаса прочности по нормальным напряжениям:

.

Коэффициент S_Tτ запаса прочности по касательным напряжениям:

.

Общий коэффициент S_Т запаса прочности по пределу текучести:

;

полученное значение S_T также превышает минимально допустимое значение [S_T] = 1,3…2,0.

5.29. Коэффициенты запаса прочности в опасных сечениях значительно превосходят минимально допустимые значения, следовательно, расчет на жесткость не требуется.

Библиографический список

1. Дунаев П. Ф., Леликов О. П. Конструирование узлов и деталей машин: Учеб. пособие для техн. спец. вузов – 5-е изд., перераб. и доп.- М.: Высш. шк., 1998. - 447 с., ил.

2. Благовестный А. С. Разработка эскизного проекта тихоходного вала редуктора: Методические указания к лабораторно - практич. занятиям для студентов, изучающих дисциплины: «Механика», «Техническая механика», «Детали машин и основы конструирования» / Юж. - Рос. гос. техн. ун-т (НПИ).- Новочеркасск: ЮРГТУ, 2003. - 11 с.

3. Иванов М. Н. Детали машин: Учеб. для студентов втузов / Под ред. В. А. Финогенова.- 6-е изд., перераб.- М.: Высш. шк., 2000. - 383 с.: ил.

4. Иосилевич Г. Б. Детали машин: Учеб. для студентов машиностроит. спец. вузов.- М.: Машиностроение, 1988. – 368 с.: ил.

5. Решетов Д. Н. Детали машин: Учеб. для студентов машиностроительных и механических специальностей вузов. – 4-е изд., перераб. и доп. – М.: Машиностроение, 1989. – 496 с.: ил.

Учебно-практическое издание