17. Электродинамика в релятивистских обозначения
17.1. Показать, что скалярное произведение двух четырехвекторов, определяемое соотношением (17.3), инвариантно относительно преобразований Лоренца (17.1).
Указание. Записать скалярное произведение через компоненты четырехвекторов и применить к каждой из компонент преобразование Лоренца.
17.2. Вычислить квадрат четырехвектора скорости.
17.3. Построить четырехвектор ускорения и вычислить его квадрат.
17.4. Показать, что с точки зрения математики проблема выбора потенциалов в калибровке Лоренца сводится к решению неоднородного уравнения Д′Аламбера.
Указание. В случае если для выбранных векторного и скалярного потенциалов условие калибровки Лоренца не выполняется, дивергенция векторного потенциала и производная по времени скалярного могут отличаться не более чем на скалярную функцию.
17.5. Найти явное выражение для оператора Лапласа, записанного в сферических координатах. Упростить полученное выражение для частного случая применения оператора Лапласа к сферически симметричной функции (зависящей только от расстояния от начальной точки).
17.6. Выполнить выкладки, пропущенные при выводе неоднородного уравнения Д′Аламбера для скалярного потенциала (17.17).
17.7. Выполнить без ошибок все вычисления и получить приведенное в примере окончательное выражение (17.26) для электрического поля, создаваемого расположенным в начале координат переменным диполем. Упростить выражение (17.26) для случая вычисления электрического поля на больших расстояниях от диполя.
Подобно тому как это было сделано в примере, обоснуйте релятивистские формулы преобразования магнитных полей (18.7).
Используя соотношения (18.7) и приобретенные навыки решения задач электростатики, рассчитайте магнитные поля, создаваемые:
а) равномерно движущимся с нерелятивистской скоростью равномерно заряженным по объему шаром;
б) равномерно заряженным по объему длинным цилиндром, движущимся с заданной скоростью в направлении, параллельном его оси;
в) равномерно заряженным по объему длинным цилиндром, движущимся с заданной скоростью в направлении, перпендикулярном его оси.
Равномерно заряженный по поверхности длинный цилиндр заданного радиуса равномерно катится без проскальзывания по гладкой горизонтальной плоскости. Найти электромагнитное поле, создаваемое цилиндром.
Указание. Перейти к системе отсчета, в которой ось цилиндра остается неподвижной.
18.4. Исходя из изложенного релятивистского описания электромагнитных взаимодействий, обоснуйте основные утверждения о свойствах электрического поля равномерно движущегося заряда, приведенные в лекции 9.
Задания для моделирования на компьютере
Собранные в этом разделе задачи представляют собой задания для небольших самостоятельных исследований, выполнение которых подразумевает активное использование численного моделирования на компьютерах. Приведенные задачи могут быть решены сравнительно легко в случае использования профессиональных пакетов программ для численного моделирования физических процессов и систем. Организация подобной деятельности студентов преследует следующие цели:
вовлечение студентов в процесс активного, творческого изучения углубленного теоретического материала на примерах, как правило не допускающих аналитического описания,
приобретение профессиональных навыков работы с пакетами моделирующих программ при решении задач физики, изучение структуры и возможностей этих пакетов;
знакомство с методами и алгоритмами численного моделирования;
приобретение опыта интерпретации результатов численного моделирования физических процессов.
При решении задач с использованием компьютерного моделирования следует уделять внимание не только решению проблемы достижения максимальной точности результатов, но и их оформлению и соответствии с современными требованиями дизайна для элек4тронной продукции.
Предлагаемые задачи также могут решаться и без использования готовых моделирующих программ в результате создания собственных оригинальных разработок. При таком подходе трудозатраты, необходимые для качественного выполнения подавляющего большинства приведенных заданий позволяют их рассматривать в качестве заданий для курсовых работ, при выполнении которых учащиеся приобретают весьма востребованный сегодня опыт численного моделирования и программирования на алгоритмических языках высокого уровня.
При изучении курса физики выполнение «компьютерных лабораторных работ» в обязательном порядке должно сочетаться с прохождением физического практикума в учебных лабораториях. При обработке результатов измерений, выполненных в учебных лабораториях, так же целесообразно использования вычислительной техники.
Рекомендуемые по каждой из тем курса лабораторные работы физического практикума размещены совместно с заданиями для компьютерного моделирования.
ЭЛЕКТРОСТАТИКА
1.К1. Попытайтесь «научить» Ваш компьютер моделировать движение заряженных частиц в электростатическом поле задаваемой пользователем пространственной конфигурации. Проверьте правильность работы моделирующей программы на простейших примерах движения частицы в постоянном электрическом поле. Воспроизведите результаты численного эксперимента по движению зарядов в центральном поле, напряженность которого уменьшается с расстоянием по закону E ~ 1/r (рис. 1.7,б). Изучите особенности движения частиц в центральном поле вида E~rα для различных значений α.
1.К2. Попытайтесь «научить» Ваш компьютер рассчитывать напряженность электростатического поля и потенциал, создаваемые произвольно задаваемым распределением точечных зарядов, в определяемой пользователем точке пространства. Проверьте правильность работы моделирующих программ на частных примерах, допускающих простой аналитический расчет.
2.К1. Попытайтесь составить программу для Вашего компьютера, которая по задаваемому Вами пространственному распределению потенциала позволяла бы рассчитывать напряженность электрического поля в заданной точке пространства.
Указание. Программу желательно составить так, чтобы распределение потенциала можно было задавать не только с помощью аналитических выражений, но и численно (в виде массива значений φ для большого числа близко расположенных точек).
3.К1. Попытайтесь освоить технику компьютерных расчетов пространственных распределений потенциалов и напряженностей электростатических полей в системах типа «заряды + проводники» на основе численного решения уравнения Пуассона, используя пакеты моделирующих программ (Ansys, Femlab или их аналоги). Начните с моделирования простейших систем (заряд вблизи проводящей плоскости, заряд и заземленная сфера и т.д.). Создайте модели электростатических систем с проводниками сложной конфигурации. Какие общие закономерности для распределений напряженности поля и потенциала наблюдаются в таких системах?
3.К2. Используя пакеты для компьютерного моделирования электростатических полей в системах с проводниками, сравните получаемые с их помощью результаты с данными расчетов методом изображений, которые также могут быть выполнены на компьютере. Обратите внимание на систематическое ухудшение соответствия результатов вблизи резких изломов проводящих поверхностей (например, у вершины двугранного угла, образованного проводящими плоскостями, на биссектрисе которого помещен электрический заряд). Чем можно объяснить ухудшение качества результатов? Как повысить точность моделирования в указанных «опасных» областях?
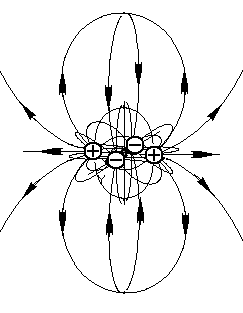
4.К1. Используя имеющиеся в Вашем распоряжении программные средства, смоделируйте на компьютере электростатические поля, соответствующие нескольким первым слагаемым мультиполь-ного разложения (4.1). Попытайтесь подобрать простые распределения точечных зарядов, электрические поля которых на достаточном удалении совпадают с полями, возникающими при разложении по мультиполям. В качестве примера на рис. изображены простая система зарядов и силовые линии ее электрического поля. На расстояниях, превышающих характерные размеры системы, это поле совпадает с электрическим полем, описываемым третьим (квадрупольным) слагаемым суммы (4.1).
4.К2. Пользуясь компьютерным моделированием и сведениями из элементарного курса химии, покажите, что напряженность электрического поля, создаваемого молекулой воды на достаточно больших расстояниях от нее, практически совпадает с напряженностью поля электрического диполя.
4.К3. Попытайтесь разработать компьютерные модели, иллюстрирующие поведение электрического диполя во внешнем электростатическом поле различной конфигурации: пространственно однородном и обладающем отличным от нуля градиентом. Создайте аналогичные компьютерные демонстрации для электрического квадруполя.
5.К1. Попытайтесь выполнить задания 3.К1 и 3.К2 для случая электростатических систем, содержащих заряды и диэлектрики.
Рекомендуемые работы физического практикума:
Л.1.1. Изучение электростатических полей методом электрической ванны.
Л.1.2. Полярные молекулы.
Л.1.3. Сегнетоэлектрики.
МАГНИТОСТАТИКА
7.К1.Попытайтесь разработать оригинальную «программу-конструктор», позволяющую пользователю создавать на экране дисплея электрические цепи постоянного тока, содержащие источники ЭДС, резисторы, конденсаторы и соединительные провода и определять токи и напряжения на элементах схемы, используя «виртуальные» вольтметр и амперметр.
Указания. При составлении алгоритма расчета цепей целесообразно использовать правила Кирхгофа. При разработке современного и удобного интерфейса такой программы важно вовремя остановиться: подобное занятие весьма увлекательно, но непосредственно к физике не относится.
7.К2. Используя готовые пакеты моделирующих программ или собственные разработки, попытайтесь научиться рассчитывать электрическое сопротивление между двумя идеальными проводниками заданной формы, помещенными в вещество с малой электроповодностью.
8.К1. Создайте простейшую компьютерную модель проводника, имеющего форму шара. Внутри шара равномерно распределен положительный заряд («кристаллическая решетка») и случайным образом расположены отрицательно заряженные частицы («электроны»), способные двигаться, взаимодействуя друг с другом и «решеткой» с помощью электростатических сил и испытывая действие сил вязкого трения (зависят от скорости линейно). Исследуйте поведение созданного Вами модельного проводника во внешнем электрическом поле и в случае сообщения ему дополнительного электрического заряда. Соответствует ли численное решение, найденное для построенной модели проводящего шара, ранее полученным решениям задач электростатики проводников?
8.К2. Используйте сформулированные в задаче 8.К1 идеи для создания компьютерной модели пассивного участка цепи в виде проводника, имеющего форму вытянутого цилиндра, между торцами которого течет постоянный электрический ток. Какие дополнительные элементы следует ввести в модель для источника ЭДС? Пригодна ли созданная Вами модель проводника для демонстрации законов Ома и Джоуля—Ленца?
8.К3. Используя профессиональные пакеты компьютерного моделирования, изучите некоторые особенности протекания постоянного электрического тока по П-образному проводнику, удельная проводимость ρ–1 «перекладины» которого существенно ниже проводимости σ расположенных параллельно токоведущих частей, потенциалы торцов которых различны и поддерживаются постоянными (см. рис.). На первом этапе рассчитайте конфигурацию электрического поля в случае непроводящей «перекладины» (ρ→∞) и убедитесь, что линии электрического поля в этом случае не направлены вдоль нее оси.
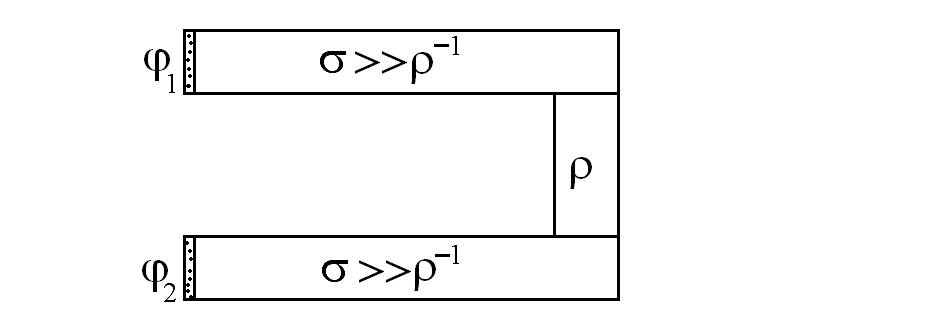
Как это согласуется с хорошо известным фактом, что протекающий с соответствии с законом Ома вдоль линий электрического поля ток направлен по оси проводника? Задайте конечное значение удельного сопротивления материала перекладины и постарайтесь получить ответ на поставленный вопрос, анализируя результаты компьютерных экспериментов
9.К1.Разработайте компьютерную программу, моделирующую движение двух взаимодействующих друг с другом заряженных частиц. Сравните результаты моделирования движения частиц в описанной системе с данными численного эксперимента, учитывающего только электростатические взаимодействия.
10.К1. Используя пакеты программ численного моделирования, попытайтесь освоить технику расчетов магнитных полей и соответствующих им векторных потенциалов, создаваемых непрерывными распределениями токов. Смоделируйте магнитные поля и потенциалы, создаваемые:
а) длинным цилиндром с равномерно распределенным по его сечению электрическим током;
б) длинным цилиндром, заряженным по объему и равномерно вращающимся вокруг своей оси;
в) равномерно заряженным по объему шаром, вращающимся вокруг своей оси с постоянной угловой скоростью.
г) шарообразным облаком из заряженных частиц, разлетающихся от центра со скоростями, пропорциональными расстояниям до него (uk ~ rk).
10.К2. Используя готовые пакеты программ или самостоятельные разработки, освойте технику моделирования магнитных полей, создаваемых отрезками прямых тонких проводников и круговыми витками с током. Смоделируйте магнитные поля соленоида, тороидальной катушки и других распределений источников, допускающих расчеты вектора B с помощью теоремы о циркуляции. Проследите за тем, как получаемые в процессе численного моделирования результаты приближаются к результатам идеализированных расчетов при увеличении линейной плотности витков с током.
11.К1. Приобретите опыт численного моделирования магнитных полей в магнитостатических системах, содержащих токи и сверхпроводники. Как и в случае электростатики (задание 3.К2), оцените результаты, сравнения их с данными, получаемыми методом изображений.
12.К1. Изучите возможности использования имеющейся у Вас программы численного моделирования для расчета электрических и магнитных полей при наличии вещества. Протестируйте моделирующие программы на следующих примерах из электростатики и магнитостатики:
а) расчет электрического (магнитного) поля заряженной нити (провода с током), находящейся в вакууме и расположенного параллельно плоской границе вещества с заданными свойствами;
б) расчет электрического (магнитного) моля во всем пространстве в случае однородного шара (или длинного цилиндра) из вещества с заданными свойствами, помещенного в однородное электрическое (магнитное) поле.
В обоих случаях обратите внимание на то, как изменяются моделируемые поля в зависимости от величины диэлектрической (магнитной) проницаемости вещества. Сравните результаты численного моделирования с расчетными. Для каких еще электрических и магнитных систем Вы можете выполнить аналогичные мини-исследования?
12.К2. Разработайте компьютерную модель, демонстрирующую изменения пространственной конфигурации магнитостатического поля, создаваемого конечным соленоидом с движущимся вдоль его оси сердечником из ферромагнетика.
Рекомендуемые работы физического практикума:
Л.2.1. Измерение токов и напряжений.
Л.2.2. Регулировка токов и напряжений.
Л.2.3. Исследование генератора электрического тока.
Л.2.4. Измерение удельного сопротивления стержней с помощью моста Томсона.
Л.2.5. Градуировка термопары.
Л.2.6. Определение работы выхода электрона из металла.
Л.2.7. Исследование кенотрона.
Л.2.8. Исследование кенотрона.
Л.2.9. Изучение магнитных свойств стали. Гистерезис.
Л.2.10. Исследование работы электромотора.
Л.2.11. Эффект Холла в металлах
Л.2.12. Эффект Холла в полупроводниках
Л.2.13. Определение ширины запрещенной зоны в германии
Л.2.14. Определение коэффициента диффузии и времени жизни носителей.
Л.2.15. Изучение температурной зависимости магнитной проницаемости.
Л.2.16. Ядерный магнитный резонанс
Л.2.17. Термоэлектронная эмиссия.
Л.2.18. Исследование характеристик транзистора с P-N переходом.
ЭЛЕКТРОДИНАМИКА
13.К1. Дополните разработанную ранее программу моделирования движения нерелятивистских заряженных частиц в электрическом поле (задача 1.К1) возможностью моделировать их движение в магнитных полях произвольной пространственной конфигурации, изменяющихся во времени по произвольному (определяемому пользователем) закону. Протестируйте Вашу программу на простейшем примере движения зарядов в однородном и не изменяющемся во времени магнитном поле. Изучите возможные формы движения зарядов в наложенных друг на друга постоянных (в пространстве и времени) электрическом и магнитном полях. Используйте программу для моделирования движения частиц в системе, описанной в условии задачи 13.10.
13.К2. Дополните разработанную программу моделирования движения частиц в электромагнитных полях (задание 13.К1) возможностью учета релятивистских эффектов (в том числе торможения радиационным трением). Сравните результаты моделирования движения частиц в постоянных электрическом и магнитном полях в случаях использования классического приближения и расчета по формулам теории относительности.
13.К3. Используйте разработанную Вами программу (задача 13.К1) для моделирования движения заряженных частиц в циклотроне (заряды движутся во взаимно перпендикулярных постоянном магнитном и переменном электрическом полях). Смоделируйте движение в настроенном в резонанс и выведенном из резонанса циклотроне. Как изменятся решения при введении сил вязкого трения?
13.К4. Используйте разработанную Вами программу (задача 13.К1) для моделирования движения заряженных частиц во взаимно перпендикулярных постоянном магнитном и равномерно вращающемся электрическом полях. Создайте модели, аналогичные описанным в задании 13.К3. Изменится ли характер движения частиц в моделируемом ускорителе, если направление вращения вектора E заменить на противоположное?
13.К5. Используйте разработанную Вами программу (задача 13.К2) для моделирования движения заряженных частиц в циклотроне (частота изменения электрического поля остается постоянной) в случае, когда становятся существенными релятивистские эффекты. Создайте модель движения заряженных частиц в ускорителе, частота изменения электрического поля которого совпадает с частотой свободного вращения нерелятивистских частиц в удерживающем магнитном поле. Усложните модель, включив в рассмотрение эффекты радиационного трения.
13.К6. Усовершенствуйте описанный в задаче 13.К5 ускоритель релятивистских частиц, введя такой закон изменения во времени удерживающего магнитного поля, чтобы в процессе разгона заряженные частицы не выходили из резонанса с ускоряющим электрическим полем. Проверьте работоспособность разработанного Вами «виртуального» синхрофазотрона, поставив соответствующий численный эксперимент. Уточните компьютерную модель ускорителя, введя в рассмотрение эффекты радиационного трения.
13.К7. Известно, что в циклотронных ускорителях нерелятивистских частиц возникает эффект группировки: первоначально обладавшие различными скоростями частицы, разгоняясь, собираются в группу, вращающуюся синхронно с изменениями ускоряющего частицы поля. Разработайте компьютерную модель, иллюстрирующую этот эффект. Сохраняется ли эффект группировки в случае ускорителя релятивистских частиц?
14.К1. Попытайтесь разработать компьютерную модель бетатрона с симметричным относительно оси полем. Весьма желательно предоставить пользователю возможность задания пространственной конфигурации магнитного поля и его зависимости от времени.
14.К2. Попытайтесь разработать программу вычисления индуктивности токоведущего контура известной формы, удельное сопротивление материала которого задано.
15.К1. Если Вам удалось создать программу для расчетов цепей постоянного тока (задача 7.К1), попытайтесь разработать ее аналог, моделирующий прохождение гармонических сигналов по линейным цепям, содержащим сопротивления, конденсаторы, катушки и трансформаторы.
Указание. Для удобства использования программы желательно предусмотреть возможность использования «виртуального» осциллографа.
15.К2. Изучите прохождение сигналов различной формы (периодических и непериодических) через описанные в задаче 15.5 простейшие фильтры. Для представления сигналов в виде суперпозиции гармонических удобно воспользоваться программами, осуществляющими численное Фурье-преобразование, которые можно найти во многих стандартных пакетах компьютерных программ по математике.
16.К1. Подумайте над созданием программы, позволяющей по заданному пространственному распределению электрической составляющей E(r) монохроматического электромагнитного поля определять ее магнитную составляющую и соответствующий полю вектор Пойнтинга.
Указание. Монохроматическим называется электромагнитное поле, электрическая и магнитная составляющие которого изменяются во времени по гармоническому закону:
16.К2. Используя имеющиеся в Вашем распоряжении моделирующие программы, изучите поведение свободного заряда в электромагнитном поле плоской монохроматической волны линейной поляризации.
16.К3. Используя имеющиеся в Вашем распоряжении моделирующие программы, изучите поведение атома Томсона (неподвижное ядро с электроном, удерживаемым в атоме упругой силой) в электромагнитном поле плоской монохроматической волны линейной поляризации. Проследите за тем, как изменяется отклик атома на воздействие поля при приближении частоты электромагнитной волны к частоте собственных колебаний электрона в атоме. Как изменится поведение модели в области резонанса в случае учета действия сил радиационного трения? Покажите, что при учете взаимодействия электрона с магнитной составляющей поля плоской монохроматической волны вынужденные колебания будут происходить не только на частоте электромагнитного поля, но и на удвоенной частоте.
16.К4. Известно, что при помещении тела в поле электромагнитной волны возникают силы, ориентированные вдоль направления ее распространения (эффект светового давления). Разработайте компьютерную модель, иллюстрирующую этот эффект на простейшем примере атома Томсона в поле плоской монохроматической электромагнитной волны.
Указание. В рамках классического описания световое давление возникает в результате действия со стороны магнитного поля световой волны силы Лоренца на движущиеся в атомах электроны, раскачиваемые электрическим полем той же волны.
Рекомендуемые работы физического практикума:
Л.3.1. Основные измерения с электронным осциллографом.
Л.3.2. Изучение электрических колебаний..
Л.3.3. Исследование колебательной системы.
Л.3.4. Исследование триода и пентода.
Л.3.5. Релаксационные колебания в цепи с неоновой лампой.
Л.3.6. Изучение катушки самоиндукции.
Л.3.7. Мост переменного тока.
Л.3.8. Исследование трансформатора.
Л.3.9. Эффект Пельтье
Вопросы для тестирования по теории
Тестирование студентов по теории проводится два раза в семестр: перед коллоквиумом и перед экзаменом. Тестирование проводится для всего потока одновременно, как правило во время последней лекции, предшествующей коллоквиуму или экзамену. Тестовые задания составляются из 10 вопросов, ответы на которые оцениваются по трехбальной шкале:
0 – ответ на вопрос заведомо ошибочный или вообще отсутствует;
½ - ответ на вопрос не достаточно полный;
1 - на вопрос дан исчерпывающий ответ.
Выбор тестовых заданий из приведенного ниже списка осуществляется случайным образом.
Тестовая работа в целом оценивается по десятибальной системе в результате простого суммирования и округления набранной суммы до ближайшего сверху целочисленного значения.
Результаты тестирования совместно с рейтингом студента предоставляются преподавателям, проводящим опрос на коллоквиуме или экзамене. В зависимости от ответа студента преподаватель может выставить любую оценку за экзамен, не зависимо от рейтинга и содержания ответов на тестовые задания. Однако, в случаях сильного расхождения оценки за тест и оценки преподавателя, ему, как правило, рекомендуется задать отвечающему несколько дополнительных вопросов по темам курса, вызвавшим затруднения у экзаменуемого во время написания теоретического теста. Эти (и другие) дополнительные вопросы в обязательном порядке заносятся экзаменатором на лист устного ответа.
В первой колонке приведенных ниже таблиц с вопросами совместно с номером приведена характеристика его относительной сложности (0 – вопрос на знание формул обязательного минимума; 1 – вопрос, требующий применения знаний списка формул обязательного минимума к конкретной ситуации; 2 – мини-задача, решение котрой не требующая сколько-нибудь существенных вычислений, но подразумевает активное владение материалом.
Задания к тесту N1
-
1. Электростатические взаимодействия
1.1.
0
Какой макроскопический заряд можно назвать точечным?
Ответ:
1.2.
0
Запишите выражение для силы, действующей на точечный заряд q1, расположенный в точке, задаваемой радиус-вектором r1, со стороны точечного заряда q2, расположенного в точке, задаваемой радиус-вектором r2.
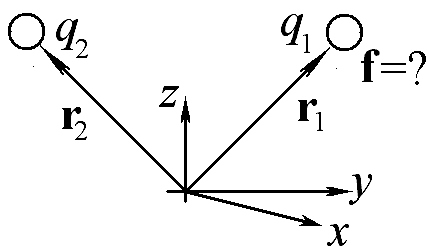
Ответ:
1.3.
0
В чем состоит принцип суперпозиции для электростатических сил?
Ответ:
1.4.
0
Запишите выражение для силы, действующей на точечный заряд Q, расположенный в точке, задаваемой радиус-вектором R, со стороны системы точечных зарядов qi, расположенных в точках, задаваемых радиус-векторами ri.
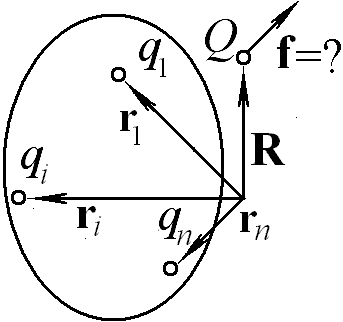
Ответ:
1.5.
0
Дайте определение напряженности электрического поля.
Ответ:
1.6.
0
Запишите выражение для напряженности электрического поля в определяемой радиус-вектором R точке пространства, создаваемого системой точечных зарядов qi, расположенных в точках, задаваемых радиус-векторами ri.
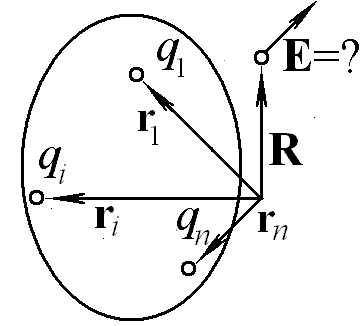
Ответ:
1.7.
0
Запишите выражение для напряженности макроскопического (усредненного) электрического поля в определяемой радиус-вектором R точке пространства, создаваемого непрерывно распределенным в пространстве электрическим зарядов, объемная плотность которого задается известной функцией ρ(r).
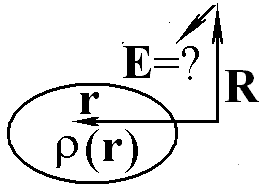
Ответ:
1.8.
0
Дайте определение электрического (скалярного) потенциала.
Ответ:
1.9.
1
Как по заданной напряженности электрического поля E(r) рассчитать потенциал в точке пространства, определяемой радиус-вектором R, если известно, что φ(R0) = 0 ?
Ответ:
1.10.
0
Запишите явное выражение для оператора пространственного дифференцирования («оператора набла») в декартовой системе координат.
Ответ:
1.11.
Запишите соотношение, позволяющее вычислить напряженность электрического поля в заданной точке пространства по заданному пространственному распределению потенциала.
Ответ:
1.12.
0
Запишите выражение для потенциала, создаваемого в определяемой радиус-вектором R точке пространства системой точечных зарядов qi расположенных в точках, задаваемых радиус-векторами ri.
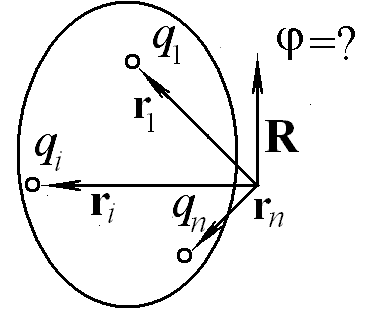
Ответ:
1.13.
1
Запишите выражение для электрического (скалярного) потенциала в определяемой радиус-вектором R точке пространства, создаваемого непрерывно распределенным в пространстве электрическим зарядов, объемная плотность которого задается известной функцией ρ(r).
Ответ:
1.14.
2
Рассчитайте напряженность электрического поля, соответствующую заданному потенциалу.
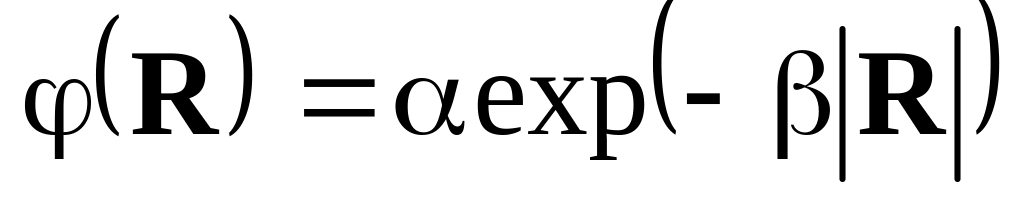
Ответ:
2. Электростатическое поле в вакууме
2.1.
1
Запишите дифференциальный аналог приведенного соотношения, в котором K – векторное поле, Z – скалярная величина, а ζ – ее объемная плотность.
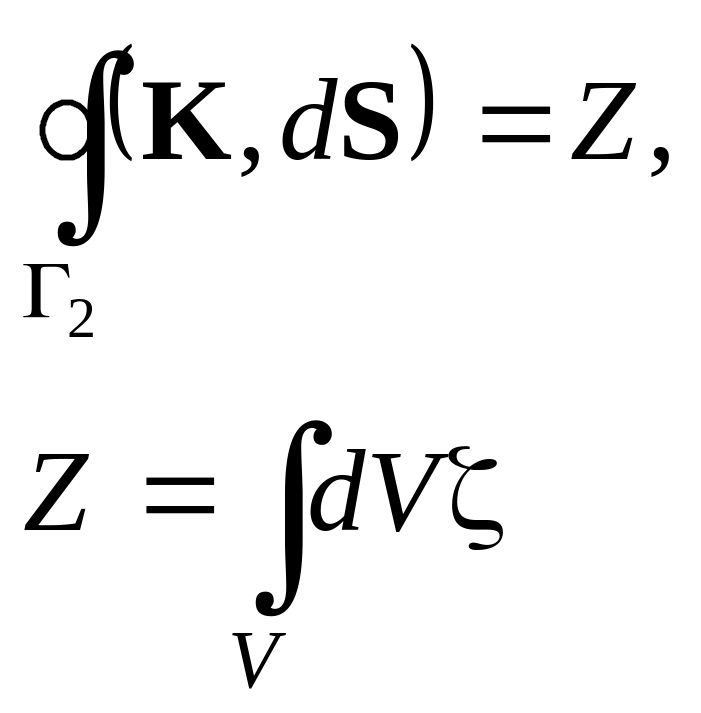
Ответ:
2.2.
1
Запишите интегральный аналог приведенного соотношения для векторного поля K.
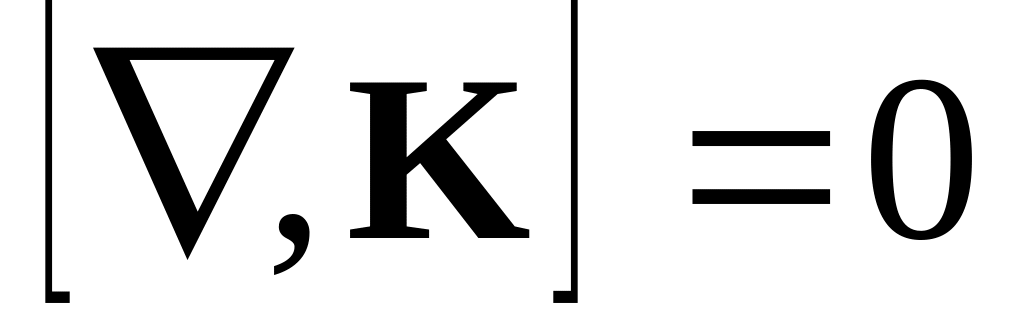
Ответ:
2.3.
0
Запишите уравнения электростатики вакуума в интегральной форме (т.е. теоремы о потоке и циркуляции векторного поля E)
Ответ:
2.4.
0
Сформулируйте теорему Гаусса для электростатического поля.
2.5.
1
Получите аналитическое выражение и постройте график зависимости величины напряженности электростатического поля от расстояния от центра сферы радиусом R, заряженной по поверхности постоянной плотностью заряда σ. (Ответ нарисовать на заготовке графика, рассчитать значения напряженности в характерных токах).
Для расчета:
Ответ:
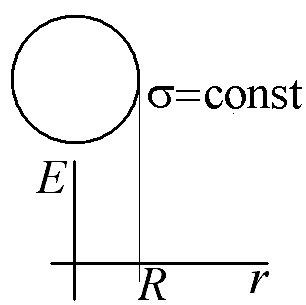
2.6.
1
Получите аналитическое выражение и постройте график зависимости величины напряженности электростатического поля от расстояния от центра шара радиусом R, заряженной по объему постоянной плотностью заряда ρ. (Ответ нарисовать на заготовке графика, рассчитать значения напряженности в характерных токах).
Для расчета:
Ответ:
2.7.
1
Постройте график зависимости величины напряженности электростатического поля от расстояния от оси бесконечного цилиндра радиусом R, заряженной по поверхности постоянной плотностью заряда σ. (Ответ нарисовать на заготовке графика, рассчитать значения напряженности в характерных токах).
Для расчета:
Ответ:
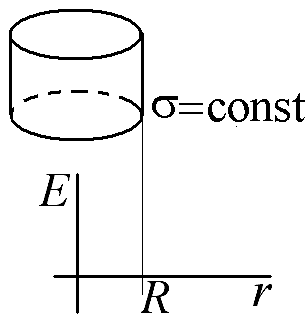
2.8.
1
Постройте график зависимости величины напряженности электростатического поля от расстояния от центра шара радиусом R, заряженной по объему постоянной плотностью заряда ρ. (Ответ нарисовать на заготовке графика, рассчитать значения напряженности в характерных токах).
Для расчета:
Ответ:
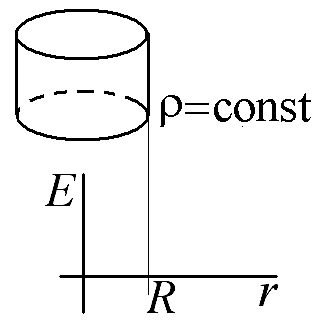
2.9.
1
Получите аналитическое выражение и постройте график зависимости от координаты x х-проекции напряженности электрического поля, создаваемого двумя разноименно заряженными (поверхностная плотность заряда ±σ) бесконечными пластинами. (Ответ нарисовать на заготовке графика, рассчитать значения напряженности в характерных токах).
Для расчета:
Ответ:
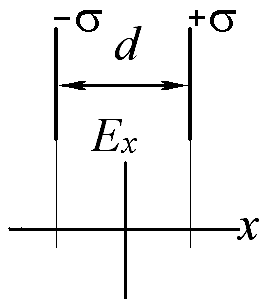
2.10.
2
Получите аналитическое выражение и постройте график зависимости от координаты x х-проекции напряженности электрического поля, создаваемого двумя одноименно заряженными (поверхностная плотность заряда +σ) бесконечными пластинами. (Ответ нарисовать на заготовке графика, рассчитать значения напряженности в характерных токах).
Для расчета:
Ответ:
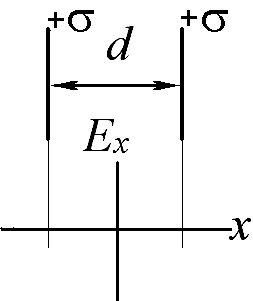
2.11.
2
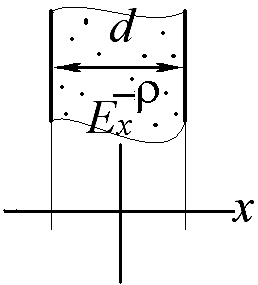
Получите аналитическое выражение и постройте график зависимости от координаты x х-проекции напряженности электрического поля, создаваемого равномерно заряженным по объему постоянной плотностью заряда –ρ<0) бесконечным плоскопараллельным слоем толщиной h. (Ответ нарисовать на заготовке графика, рассчитать значения напряженности в характерных токах).
Для расчета:
Ответ:
2.12.
1
Получите аналитическое выражение и постройте график зависимости электрического (скалярного) потенциала от расстояния от центра сферы радиусом R, заряженной по поверхности постоянной плотностью заряда σ. Потенциал бесконечно удаленной точки считать равным нулю. (Ответ нарисовать на заготовке графика, рассчитать значения потенциала в характерных токах).
Для расчета:
Ответ:
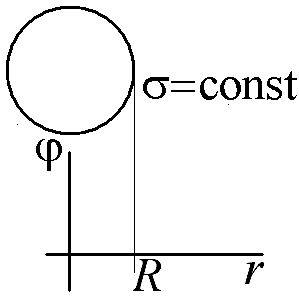
2.13.
2
Получите аналитическое выражение и постройте график зависимости электрического (скалярного) потенциала от расстояния от центра шара радиусом R, заряженной по объему постоянной плотностью заряда ρ. Потенциал бесконечно удаленной точки считать равным нулю. (Ответ нарисовать на заготовке графика, рассчитать значения потенциала в характерных токах).
Для расчета:
Ответ:
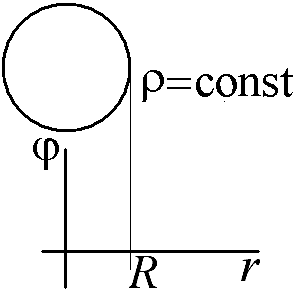
2.14.
1
Постройте график зависимости электрического (скалярного) потенциала от расстояния от оси бесконечного цилиндра радиусом R, заряженной по поверхности постоянной плотностью заряда σ. Потенциал поверхности цилиндра считать равным нулю. (Ответ нарисовать на заготовке графика, рассчитать значения потенциала в характерных токах).
Для расчета:
Ответ:
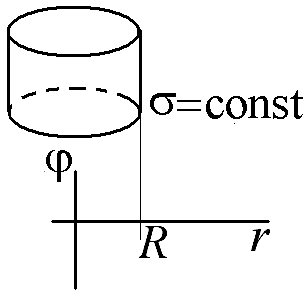
2.15.
2
Постройте график зависимости электрического (скалярного)потенциала от расстояния от центра шара радиусом R, заряженной по объему постоянной плотностью заряда ρ. Потенциал поверхности цилиндра считать равным нулю. (Ответ нарисовать на заготовке графика, рассчитать значения потенциала в характерных токах).
Для расчета:
Ответ:
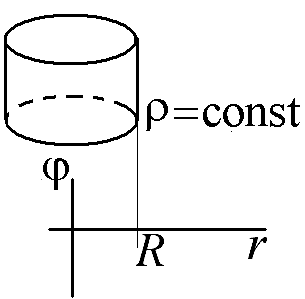
2.16.
1
Получите аналитическое выражение и постройте график зависимости от координаты x электрического (скалярного) потенциала, создаваемого двумя разноименно заряженными (поверхностная плотность заряда ±σ) бесконечными пластинами. Потенциал точки x = 0 считать равным нулю. (Ответ нарисовать на заготовке графика, рассчитать значения потенциала в характерных токах).
Для расчета:
Ответ:
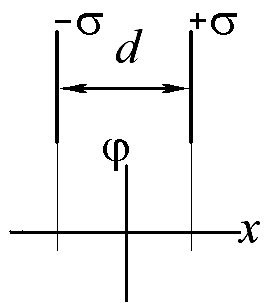
2.17.
2
Получите аналитическое выражение и постройте график зависимости от координаты электрического (скалярного) потенциала, создаваемого двумя одноименно заряженными (поверхностная плотность заряда +σ) бесконечными пластинами. За нуль принять потенциал точки х = 0. (Ответ нарисовать на заготовке графика, рассчитать значения потенциала в характерных токах).
Для расчета:
Ответ:
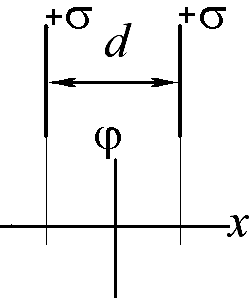
2.18.
2
Получите аналитическое выражение и постройте график зависимости от координаты x электрического (скалярного) потенциала, создаваемого равномерно заряженным по объему постоянной плотностью заряда –ρ<0) бесконечным плоскопараллельным слоем толщиной h. За нуль принять потенциал точки x=0. (Ответ нарисовать на заготовке графика, рассчитать значения потенциала в характерных токах).
Для расчета:
Ответ:
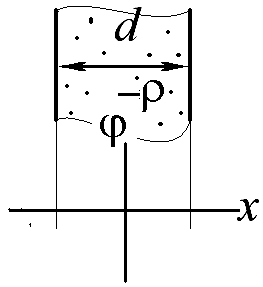
2.19.
0
Дайте определение силовой линии электрического поля.
Ответ:
2.20.
1
Запишите оператор Лапласа в декартовых координатах.
Ответ:
2.21.
0
Запишите уравнение Пуассона для скалярного потенциала.
Ответ:
2.22.
2
Найдите пространственное распределение плотности заряда ρ, по заданной напряженности электрического поля Е(R). Коэффициенты ki – постоянные.
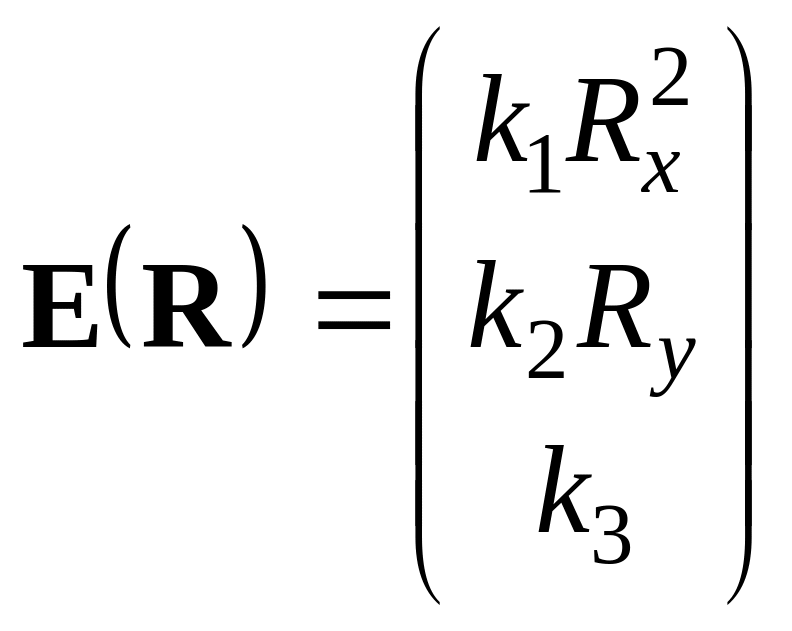
Ответ:
2.23.
2
Найдите пространственное распределение плотности заряда ρ, по заданной напряженности электрического поля Е(R).
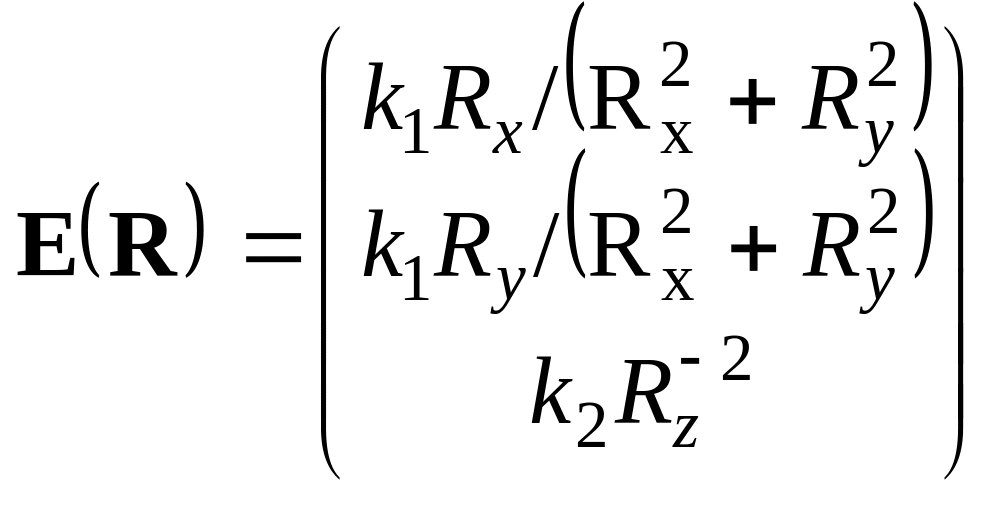
Ответ:
2.24.
2
По заданному потенциалу найти распределение плотности зарядов
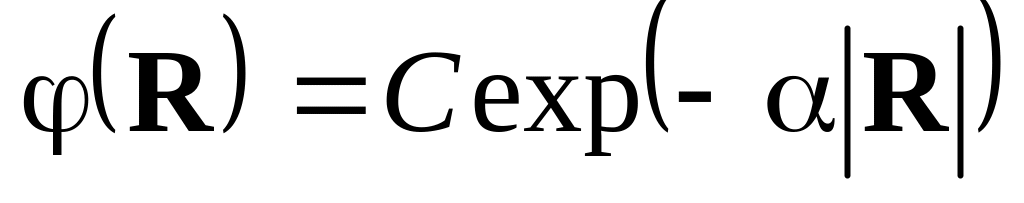
Для вычислений:
Ответ:
2.25.
2
Напряженность сферически симметричного электрического поля изменяется с расстоянием в соответствии с приведенным графиком. Построить график зависимости потенциала от расстояния. Потенциал бесконечно удаленной точки считать равным нулю.
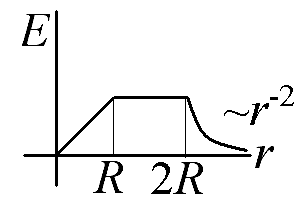
Ответ:
2.26.
2
Напряженность сферически симметричного электрического поля изменяется с расстоянием в соответствии с приведенным графиком. Построить график зависимости плотности заряда от расстояния.
Ответ:
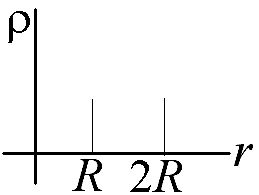
3. Электростатическое поле при наличии проводников
3.1.
0
Что можно сказать об электростатическом поле и потенциале в объеме, заполненном проводящим веществом?
Ответ:
3.2.
0
Запишите граничные условия для вектора напряженности электростатического поля для случая границы «вакуум — проводник».
Ответ:
3.3.
1
По заданной напряженности электростатического поля вблизи плоской и поверхности проводника z = 0 рассчитать распределение зарядов на поверхности проводника.
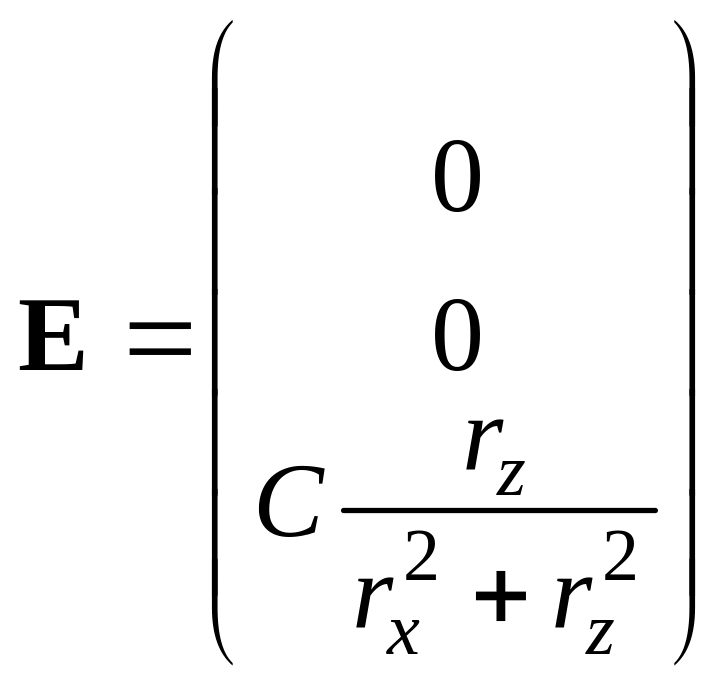
Ответ:
3.4.
1
Найти силу, действующую на точечный заряд q, расположенный на расстоянии h от плоской поверхности заземленного проводника.
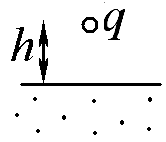
Ответ:
3.5.
1
Точечный заряд q > 0 расположен на биссектрисе двугранного угла, образованного двумя заземленными проводящими плоскостями. Постройте систему зарядов-изображений, позволяющих вычислить силу, действующую на точечный заряд.
Ответ:
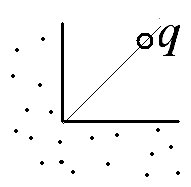
3.6.
2
Точечный заряд q > 0 помещен внутрь изолированного проводящего сферического слоя, заряд которого равен нулю. Нарисуйте примерный вид линий электрического поля во всем пространстве.
Ответ:
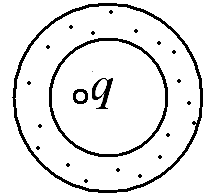
3.7.
2
Точечный заряд q > 0 помещен внутрь изолированного проводящего сферического слоя, которому сообщен равный по величине и противоположный по знаку заряд. Нарисуйте примерный вид линий электрического поля во всем пространстве.
Ответ:
3.8.
1
Незаряженный проводящий шар помещен в однородное электрическое поле. Нарисуйте примерную картину силовых линий.
Ответ:
3.9.
1
Сформулируйте теорему единственности решения задач электростатики при наличии проводников.
Ответ:
3.10.
2
Найти силу, действующую на единицу длины бесконечной нити, равномерно заряженной линейной плотностью заряда λ, расположенной на расстоянии h от плоской поверхности проводника, параллельно этой поверхности.
Решение:
Ответ:
4. Механизмы поляризации диэлектриков
4. 1.
1
Дайте определение вектора дипольного момента электрического диполя (необходимые для определения величины можно отметить на рисунке).
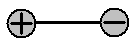
Ответ:
4.2.
0
Какую величину называют поляризуемостью молекулы?
Ответ:
4.3.
2
Оцените поляризуемость атома Томсона, если заряд и масса его электронного облака соответственно равны Q и m, а собственная частота колебаний электронного облака равна ω0.
Решение:
Ответ:
4.4.
1
Чему равна потенциальная энергия электрического диполя с моментом d, если он помещен в однородное электрическое поле с напряженностью E?
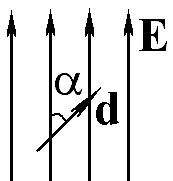
Ответ:
4.5.
2
Какую работу нужно совершить для того, чтобы расположенный на расстоянии R от точечного заряда q электрический диполь с моментом d, ориентированным точно на заряд, повернуть на 180о? Точечный заряд при этом остается неподвижным.
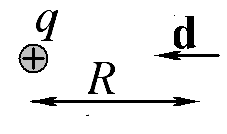
Ответ:
4.6.
2
Газ из дипольных молекул (момент каждой молекулы равен d0) gпомещен в однородное электростатическое поле. Нарисуйте примерный график зависимости среднего дипольного момента молекул газа от величины напряженности поля при двух температурах: Т1 и Т2=2 Т1.
Ответ:
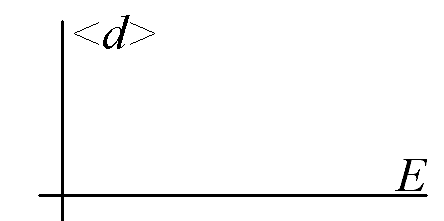
4.7.
2
Рассчитайте величину наведенного дипольного момента у анизотропной молекулы с заданной поляризуемостью α, помещенной в заданное электрическое поле E.
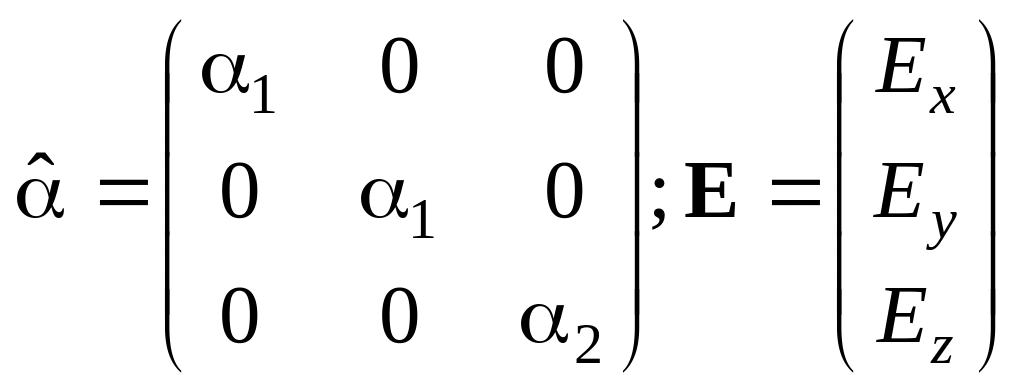
Ответ:
5. Электростатическое поле при наличии диэлектриков
5.1.
1
Дайте определение вектора поляризации P.
Ответ:
5.2.
0
Чему равна дивергенция вектора поляризации?
Ответ:
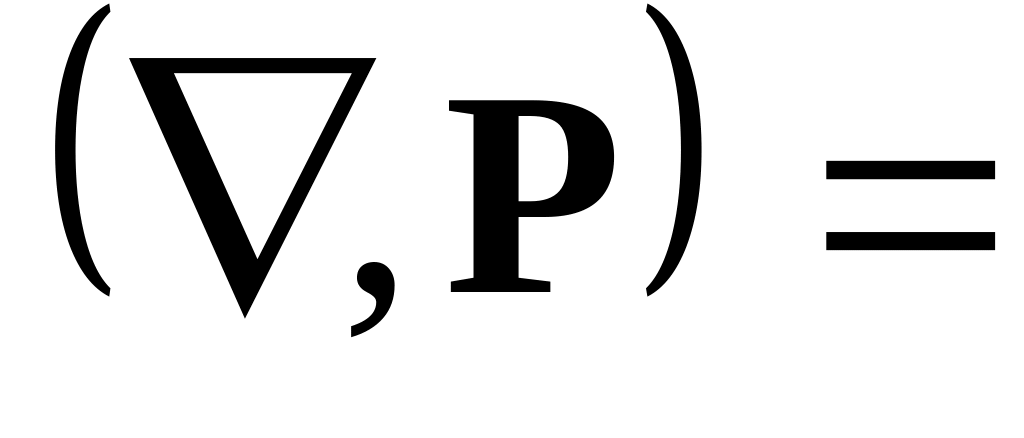
5.3.
1
Чему равен поток вектора поляризации через произвольную замкнутую поверхность?
Ответ:
5.4.
0
Дайте определение вектора D (электрической индукции)
Ответ:
5.5.
0
Дайте определение диэлектрической проницаемости вещества ε.
Ответ:
5.6.
1
Как связана диэлектрическая проницаемость ε газа с концентрацией его молекул n и их средней поляризуемостью α?
Ответ:
5.7.
0
Чему равны дивергенции векторов E и D в диэлектрике?
Ответ:
5.8.
0
Чему равны потоки через произвольные замкнутые поверхности векторов E и D в диэлектрике?
Ответ:
5.9.
2
По заданной электрической индукции и тензору диэлектрической проницаемости найти напряженность электрического поля в диэлектрике.
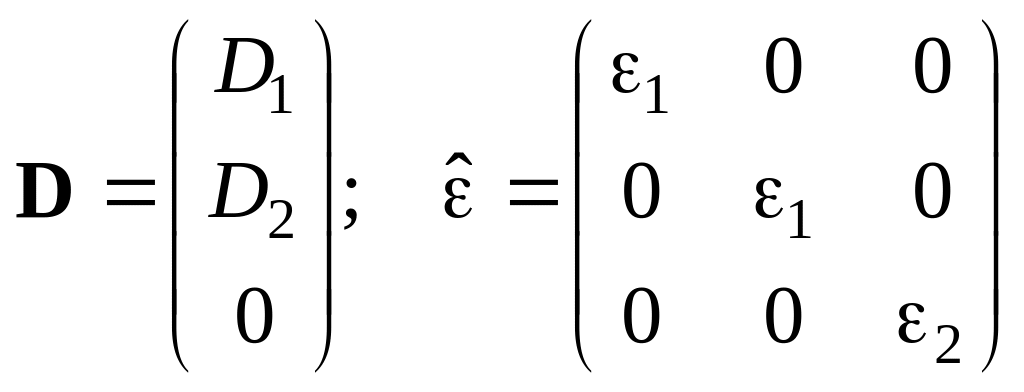
Ответ:
5.10.
0
Запишите уравнения электростатики диэлектриков в дифференциальной форме.
Ответ:
5.11.
0
Запишите уравнения электростатики диэлектриков в интегральной форме.
Ответ:
5.12.
1
Металлический шар радиусом R, заряженный положительным зарядом Q, помещен внутрь проводящего изолированного незаряженного сферического слоя радиусами 2R и 3R, заполненного однородным диэлектриком с проницаемостью ε=2. Построить графики зависимостей величин векторов E и D от расстояния до центра шара.
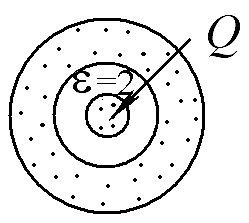
Ответ:
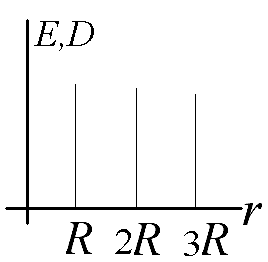
5.13.
2
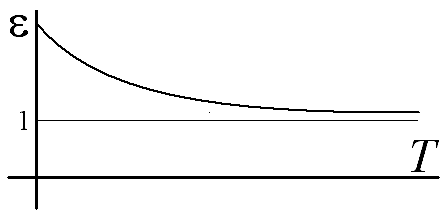
На графике приведена зависимость диэлектрической проницаемости некоторого гипотетического газа из полярных молекул от температуры (плотность газа поддерживается постоянным). В тех же координатах постройте примерный график аналогичной зависимости для газа с вдвое меньшей плотностью.
Ответ:
5.14.
2
Точечный заряд q расположен на высоте h над плоской границей однородного изотропного диэлектрика с проницаемостью ε. Рассчитать силу, действующую на заряд со стороны диэлектрика.
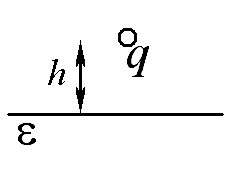
Ответ:
5.15.
2
Точечный заряд q расположен на высоте h над плоской границей однородного изотропного диэлектрика с проницаемостью ε=2. Дорисовать примерную картину силовых линий электрического поля.
Ответ:
5.16.
2
Точечный заряд q расположен на высоте h над плоской границей однородного изотропного диэлектрика с проницаемостью ε=2. Дорисовать примерную картину силовых линий векторного поля D.
Ответ:
5.17.
1
Нарисовать примерную картину силовых линий электрического поля, создаваемого однородно поляризованным шаром (внутри и вне шара).
Ответ:
5.18.
0
Запишите граничные условия для векторов E и D в случае двух диэлектриков с проницаемостями ε1 и ε2.
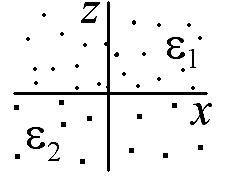
Ответ:
6, Энергия электростатического поля
6.1.
0
Энергия электростатического взаимодействия системы точечных зарядов qi, расположенных в точках ri дается известной формулой. Запишите выражение для φi.
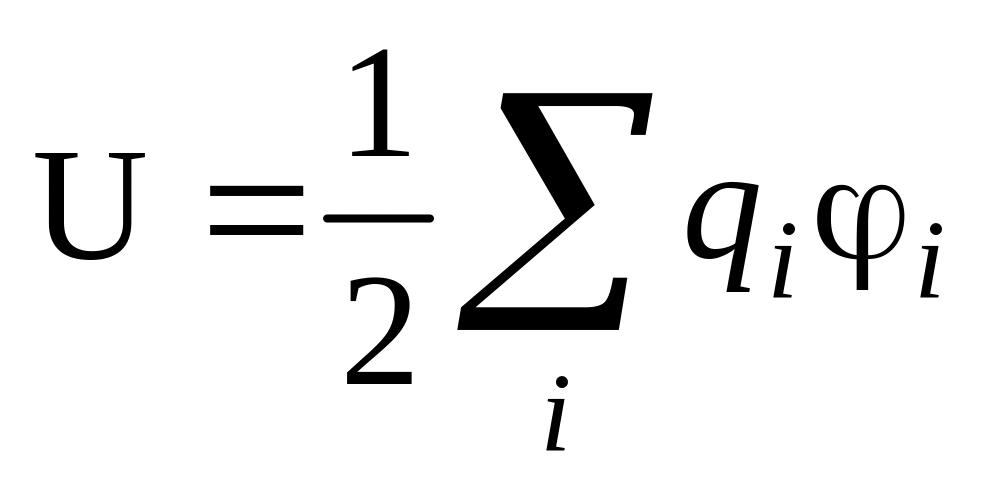
Ответ:
qi=
6.2.
0
Некоторое тело объемом V заряжено с объемной плотностью заряда ρ. Запишите формулу для расчета электростатической энергии этого тела, если задано пространственное распределение потенциала φ(r).
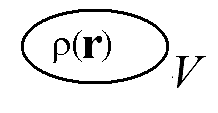
Ответ:
6.3.
1
Металлический шар радиусом R сообщен электрический заряд Q. Рассчитайте электростатическую энергию шара.
Ответ:
6.4.
0
Уединенному проводнику, емкость которого равна C, сообщили электрический заряд Q. Чему равна электростатическая энергия проводника?
Ответ:
6.5.
2
В невесомости капля ртути объемом V, имеющая электрический заряд Q, разделилась на две одинаковые капли. Какая энергия выделилась при этом? Эффектами, связанными с поверхностным натяжением, пренебречь.
Ответ:
6.6.
0
В некотором объеме пространства V создано электрическое поле, напряженность которого задается известной функцией E(r). Запишите общее выражение для вычисления электростатической энергии, заключенной в этом объеме пространства.
Ответ:
6.7.
1
Запишите общее выражение для объемной плотность электростатической энергии в диэлектрике, если векторы E и D заданы в каждой его точке.
Ответ:
6.8.
2
В некотором объеме V, заполненном газом из молекул с поляризуемостью α, концентрация которых изменяется по известному закону n(r) создано однородное электрическое поле E. Запишите выражение для расчета электрической энергии в этом объеме.
Ответ:
6.9.
2
Металлический шар радиусом R, имеющий электрический заряд q, помещен в однородный диэлектрика с проницаемостью ε. Рассчитайте электростатическую энергию системы.
Ответ:
6.10.
2
В объеме V, заполненным однородным анизотропным диэлектриком с заданным тензором диэлектрической проницаемости ε создано однородное электрическое поле E=E1ex+E2ey. Рассчитать электростатическую жэнергию объема.
Ответ:
6.11.
2
В некотором объеме пространства V задано распределение потенциала φ(r) Запишите общее выражение для вычисления электростатической энергии этого объема, если в каждой его точке ε=1.
Ответ:
7. Постоянный электрический ток
7.1.
0
Запишите общее выражение для вычисления силы тока через заданную поверхность S, если известно распределение плотности тока j(r) во всем пространстве.
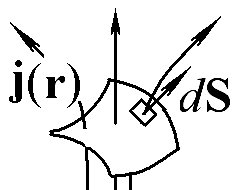
Ответ:
7.2.
0
Запишите закон сохранения электрического заряда в интегральной форме.
Ответ:
7.3.
0
Запишите закон сохранения электрического заряда в дифференциальной форме.
Ответ:
7.4.
0
Запишите закон Ома для пассивного участка цепи (в дифференциальной форме).
Ответ:
7.5.
0
Запишите законы Кирхгофа для расчета электрических цепей со сосредоточенными параметрами.
Ответ:
7.6.
0
Запишите закон Джоуля-Ленца в дифференциальной форме.
Ответ:
7.7.
Запишите закон Джоуля-Ленца в интегральной форме.
Ответ:
7.8.
1
Два проводника произвольной формы помещены в однородную изотропную среду с диэлектрической проницаемостью ε и малой удельной проводимостью σ. Чему равно электрическое сопротивление между проводниками, если их взаимная емкость равна C?
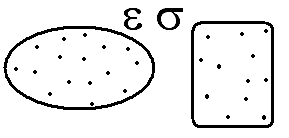
Ответ:
7.9.
2
Металлический шар радиусом R помещен в безграничную однородную изотропную среду с диэлектрической проницаемостью ε и малой удельной проводимостью σ. Шару сообщен электрический заряд Q. Через какой промежуток времени заряд шара уменьшится в е раз?
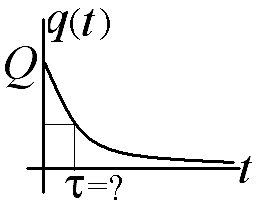
Ответ:
7.10.
2
Два соосно расположенные хорошо проводящие цилиндра высотой h радиусами R1 и R2 соответственно помещены в однородную изотропную среду с малой удельной проводимостью σ и диэлектрической проницаемостью ε. Рассчитайте электрическое сопротивление между цилиндрами.
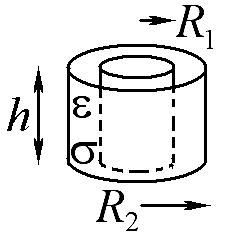
Ответ:
Электрический ток в различных средах
8.1.
1
В рамках классической модели проводимости металлов показать, что удельное сопротивление проводника пропорционально корню из температуры электронного газа.
Доказательство:
8.2.
1
Оценить энергию ионизации атома водорода в рамках планетарной модели атома (электрон движется по круговой орбите радиусом r).
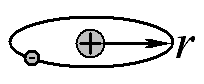
Решение:
8.3.
2
Оценить энергию ионизации атома водорода в рамках модели атома Томсона (электронное облако представляет собой равномерно заряженный шар радиусом r).
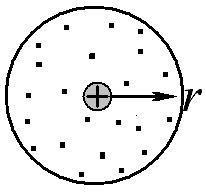
Решение:
8.4.
1
На графике приведена упрощенная вольт-амперная характеристика вакуумного диода при некоторой температуре нагреваемого катода. На том же графике нарисуйте вольт-амперную характеристику того же устройства при более высокой температуре катода.
Ответ:
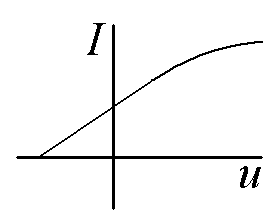
8.5.
0
Нарисуйте простейшую электрическую схему для изучения вольт-амперной характеристики вакуумного диода.
Ответ:
8.6.
0
Нарисуйте простейшую схему однополупериодного выпрямителя с полупроводниковым диодом.
Ответ:
8.7.
1
Нарисуйте простейшую схему двухполупериодного выпрямителя на полупроводниковых диодах.
Ответ:
8.8.
0
Что такое собственный полупроводник с точки зрения зонной теории кристаллов?
Ответ:
8.9.
1
Какие атомы необходимо внедрить в кристалл германия для получения примесного полупроводника n-типа?
Ответ:
8.10.
Какие атомы необходимо внедрить в кристалл кремния для получения примесного полупроводника p-типа?
Ответ:
8.11
2.
На рисунке изображена схема энергетических состояний кристалла, проявляющего диэлектрические свойства. Нарисуйте аналогичную схему для проводника при температурах, близких к абсолютному нулю.
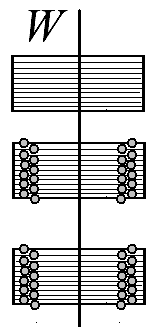
Ответ:
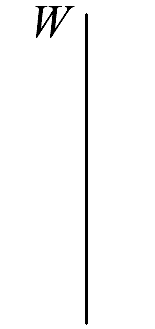
8.12.
2
На рисунке изображена схема энергетических состояний кристалла, проявляющего диэлектрические свойства. Нарисуйте аналогичную схему для собственного полупроводника при температурах, близких к абсолютному нулю. Укажите C- V-зоны. Отразите на схеме механизм возникновения основных носителей.
Ответ:
8.13.
2
На рисунке изображена схема энергетических состояний кристалла, проявляющего диэлектрические свойства. Нарисуйте аналогичную схему для примесного полупроводника n-типа при температурах, близких к абсолютному нулю. Отразите на схеме механизм возникновения основных носителей.
Ответ:
8.14.
2
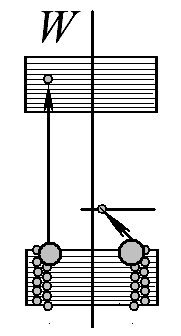
Схема энергетических состояний какого типа полупроводникового кристалла изображена на рисунке? Укажите на схеме частицы или квазичастицы, являющиеся основными носителями в полупроводниках данного типа.
Ответ:
8.15.
2
Какой полярности напряжение нужно приложить к изображенному на рис. полупроводниковому кристаллу для того, чтобы через него потек электрический ток? (Для ответа достаточно поставить знаки «+» и «–»).
Ответ:
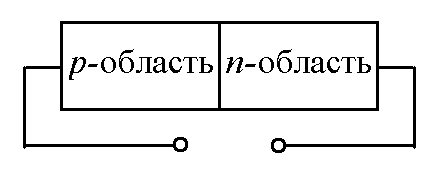
8.16.
1
Какие элементарные процессы играют доминирующую роль при образовании свободных электронов и ионов в газовом разряде (низкотемпературной плазме)?
Ответ:
Задания к тесту N2
-
9. Электрическое поле равномерно движущегося заряда
9.1.
1
Как изменяются направленная вдоль движения (E||) и нормальная к скорости (E┴) составляющие напряженности электрического поля при переходе к движущейся системе отсчета?
Ответ:
9.2.
1
Изобразите картину силовых линий точечного заряда, движущегося со скоростью, сравнимой с С.
Ответ:
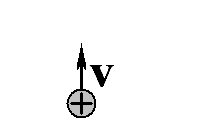
9.3.
0
В однородном электростатическом поле E движется частица с зарядом q и массой покоя m. Запишите уравнение ее движения, учитывающее релятивистские эффекты. (В качестве примера приведено аналогичное уравнение движения для нерелятивистской частицы).
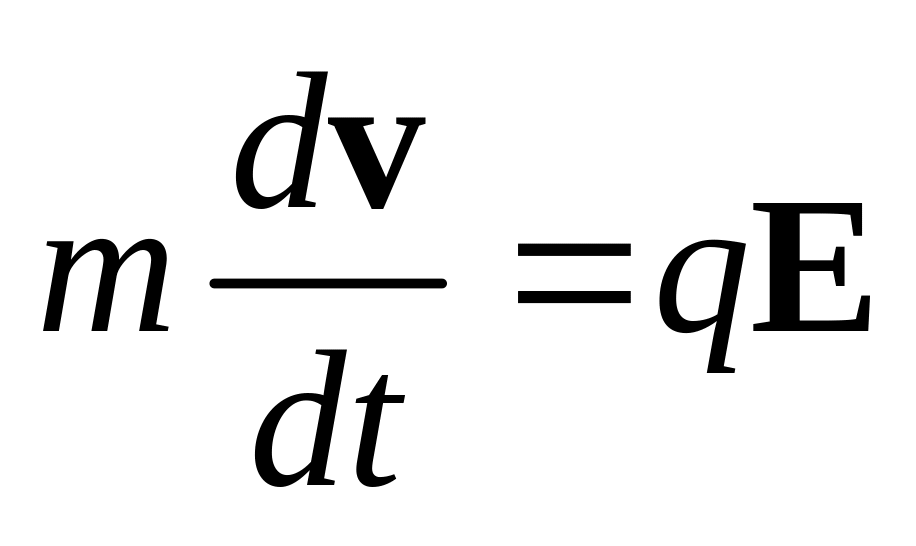
Ответ:
9.4.
0
Два электрических заряда q1 и q2 движутся в одном направлении на расстоянии d друг от друга с равными скоростями u1 = u2 . Вычислите силу взаимодействия между зарядами, регистрируемую неподвижными наблюдателями.
Ответ:
9.5.
0
Запишите выражение для вектора индукции магнитного поля, создаваемого в заданной точке пространства R системой точечных зарядов qi, расположенных в точках ri и движущихся с заданными скоростями ui.
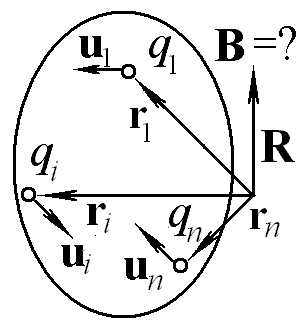
Ответ:
9.6.
0
Запишите общее выражение для индукции магнитного поля, создаваемой в данной точке пространства R произвольной системой зарядов, движущихся с одинаковыми скоростями ui = u, если известно, что аналогичная система неподвижных зарядов создает в указанной точке электрическое поле Е.
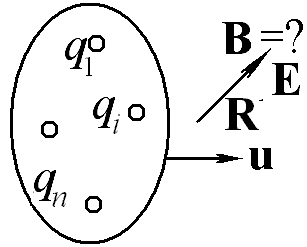
Ответ:
9.7.
0
Запишите общее выражение для магнитной индукции в заданной точке пространства R, создаваемой заданным распределением плотности токов j(r).
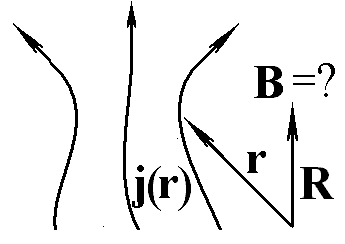
Ответ:
9.8.
0
Запишите общее выражение для магнитной индукции в заданной точке пространства R, создаваемой током I, протекающим по проводнику заданной формы.
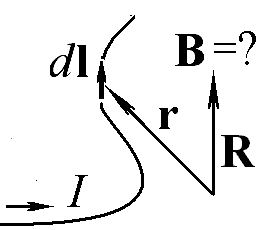
Ответ:
9.9.
0
Запишите (желательно в векторной форме) выражение для силы, действующей на точеный заряд q, движущийся со скоростью u в магнитном поле с индукцией B.
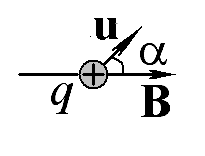
Ответ:
9.10.
0
Запишите (желательно в векторной форме) выражение для силы, действующей на участок провода δl, по которому протекает ток I, если проводник помещен в магнитное поле с индукцией B
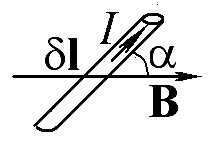
Ответ:
9.11.
1
Дайте определение вектора магнитного момента небольшого контура с током I в частном случае, когда он представляет собой круговую петлю радиусом R. (Направление вектора m можно указать прямо на рисунке).
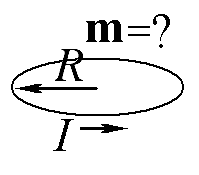
Ответ:
9.12.
1
Запишите (желательно в векторной форме) выражение для момента сил, приложенных к магнитному диполю с магнитным моментом m, помещенному в магнитное поле с индукцией B.
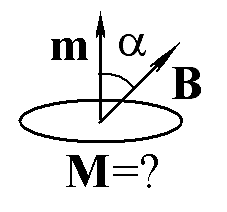
Ответ:
9.13.
1
На приведенном рисунке изобразите магнитные силы, действующие на каждый из движущихся зарядов.
Ответ:
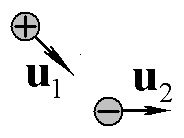
9.14.
0
Найдите вектор B на расстоянии h от прямого бесконечного провода с током I (вычислить величину вектора и указать его направление на рис.)
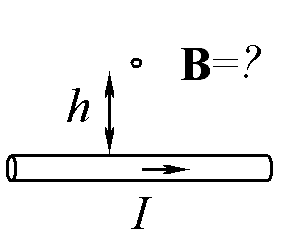
Ответ:
9.15.
1
Заряженная частица (заряд q) движется c заданной скоростью uна расстоянии h от бесконечного прямого провода с током I. Рассчитайте величину и укажите направление силы, действующей на частицу.
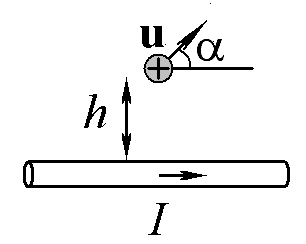
Ответ:
9.16.
2
Найдите вектор B на высоте h над бесконечной плоскостью, по которой течет ток с постоянной поверхностной плотностью i.
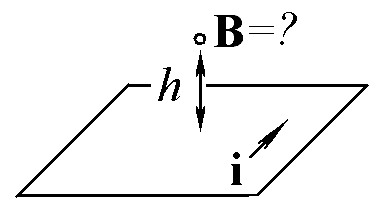
Ответ:
10. Магнитное поле в вакууме
10.1.
1
Запишите соотношение, позволяющее вычислить индукцию магнитного поля по заданному векторному потенциалу А.
Ответ:
10.2.
0
Запишите явное выражение (через частные производеые) для ротора векторного поля K.
Ответ:
10.3.
1
Найдите выражение для индукции магнитного поля, определяемого заданным векторным потенциалом.
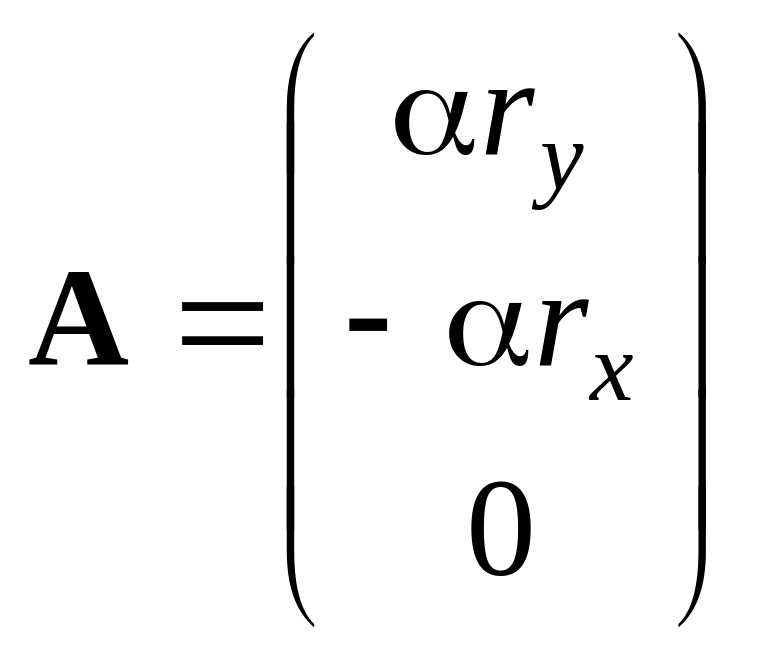
Ответ:
10.4.
0
Запишите интегральный аналог дифференциального соотношения, связывающего векторный потенциал с индукцией магнитного поля.
Ответ:
10.5.
2
Используя интегральный аналог соотношения , рассчитайте векторный потенциал однородного магнитного поля B=B0ez.
Решение:
Ответ:
10.6.
1
С точностью до какой функции определяется векторный потенциал, соответствующий заданному магнит ному полю?
Ответ:
10.7.
2
Пусть дивергенция найденного векторного потенциала А, соответствующего заданному магнитному полю, отлична от нуля и равна известной скалярной функции f(r). Найдите общее выражение для нового векторного потенциала, дивергенция которого равна нулю.
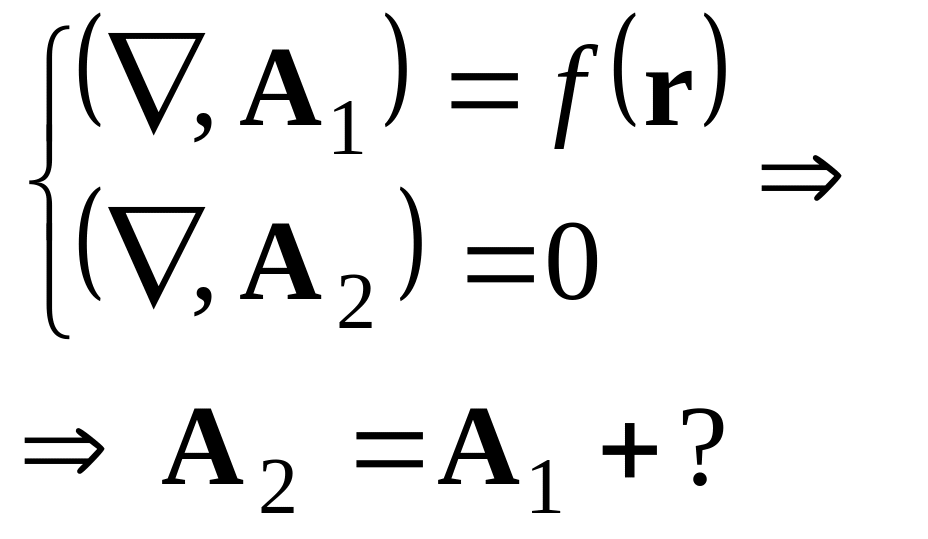
Ответ:
10.8.
1
Запишите уравнение Пуассона для векторного потенциала.
Ответ:
10.9.
1
Запишите общее выражение для векторного потенциала в заданной точке пространства R, если заданы величины всех точечных зарядов qi, их положения в пространстве ri и скорости их движения ui.
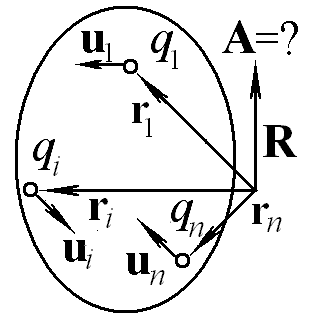
Ответ:
10.10.
1
Запишите общее выражение для векторного потенциала в заданной точке пространства R, если в каждой точке пространства r задана плотность электрического тока j(r).
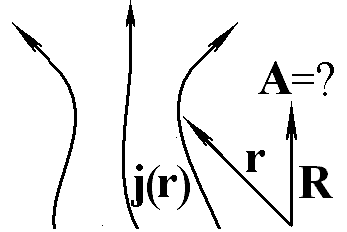
Ответ:
10.11.
0
Запишите интегральный аналог уравнения для дивергенции вектора магнит ной индукции.
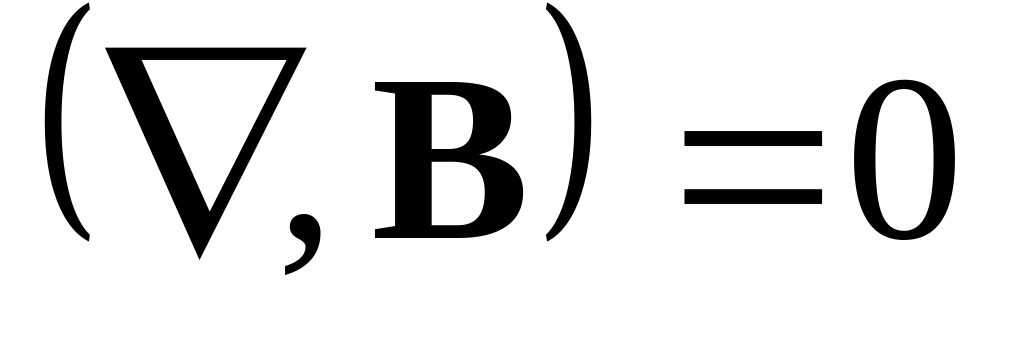
Ответ:
10.12.
0
Запишите интегральный аналог уравнения для ротора вектора магнитной индукции.
Ответ:
10.13.
0
Запишите уравнения магнитостатики вакуума в дифференциальной форме.
Ответ:
10.14.
0
Запишите уравнения магнитостатики вакуума в интегральной форме.
Ответ:
10.15.
0
Используя теорему о циркуляции вектора B и соображения симметрии, найдите величину вектора магнитной индукции на заданном расстоянии от бесконечного провода с током I.
Ответ:
10.16.
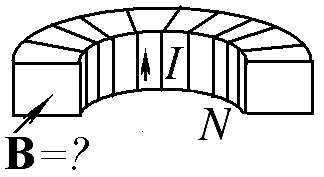
2
Используя теорему о циркуляции вектора B и соображения симметрии, найдите величину вектора магнитной индукции внутри содержащей N витков с током I кольцевой катушки с прямоугольным сечением.
Ответ:
10.17.
2
Используя теорему о циркуляции вектора B и соображения симметрии, найдите величину вектора магнитной индукции вне содержащей N витков с током I кольцевой катушки с прямоугольным сечением.
Ответ:
10.18.
1
Используя теорему о циркуляции вектора B и соображения симметрии, найдите величину вектора магнитной индукции внутри соленоида длиной h, содержащего N витков с током I.
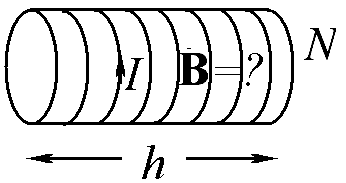
Ответ:
10.19.
0
Изобразите магнитный диполь и создаваемое им магнитное поле.
Ответ:
11. Атом в магнитном поле
11.1.
1
Что можно сказать о векторе магнитной индукции в сверхпроводящем образце и в его замкнутой области, не содержащей токов?
Ответ:
11.2.
1
Напишите выражение для энергии магнитного диполя с моментом m, помещенного в магнитное поле с индукцией B.
Ответ:
11.3.
1
Запишите общее выражение для силы, действующей на магнитный диполь с моментом m, помещенный в неоднородное магнитное поле с индукцией B(r).
Ответ:
11.4.
2
Найдите силу (величину и направление), действующую на единицу длины провода с током I, помещенного на высоте h над плоской границей сверхпроводника, параллельно этой границе.
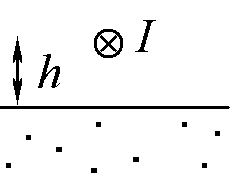
Ответ:
11.5.
1
Запишите граничные условия для нормальной и тангенциальной компонент вектора B на поверхности сверхпроводника.
Ответ:
11.6.
1
В однородное магнитное поле внесен сверхпроводящий шар. Изобразите примерный вид линий магнитного поля вблизи этого шара.
Ответ:
11.7.
2
На расстоянии h от плоской поверхности сверхпроводника (параллельно поверхности) расположен провод с током I. Найдите распределение поверхностных токов в сверхпроводнике.
Ответ:
12.1.
1
Запишите определение вектора намагниченности M.
Ответ:
12.2.
1
Запишите соотношение, связывающее вектор намагниченности и с плотностью молекулярных токов (в интегральной и дифференциальной формах)
Ответ:
12.3.
1
Запишите определение напряженности магнитного поля H
Ответ:
12.4.
0
Запишите соотношение, связывающее напряженность магнитного поля H и магнитную индукцию B в газе с концентрацией n молекул, обладающих магнитной поляризуемостью αm.
Ответ:
12.5.
1
Дайте определение магнитной поляризуемости молекулы.
Ответ:
12.6.
1
К какому типу магнетиков относится вещество, для которого μ=0?
Ответ:
12.7.
0
К какому типу магнетиков относится вещество, для которого μ>1?
Ответ:
12.8.
0
Что можно сказать о значениях магнитной проницаемости диамагнетиков?
Ответ:
12.9.
0
Что можно сказать о значениях магнитной проницаемости ферромагнетиков?
Ответ:
12.10.
2
Бесконечный прямой проводник с током I расположен параллельно плоской границе магнетика с проницаемостью μ. Рассчитайте силу, действующую на единицу длины проводника со стороны магнетика.
Ответ:
12.11.
2
Нарисовать примерный вид магнитного поля, создаваемого шаром с постоянной намагниченностью M.
Ответ:
12.12.
1
Нарисовать примерную картину линий векторного поля B в случае проводника с током, расположенного параллельно плоской поверхности сверхпроводника.
Ответ:
12.13
1
Нарисовать примерную картину линий векторного поля B в случае проводника с током, расположенного параллельно плоской поверхности диамагнетика.
Ответ:
12.14
1
Нарисовать примерную картину линий векторного поля Н в случае проводника с током, расположенного параллельно плоской поверхности диамагнетика.
Ответ:
12.15
1
Нарисовать примерную картину линий векторного поля B в случае проводника с током, расположенного параллельно плоской поверхности парамагнетика.
Ответ:
12.16.
1
Нарисовать примерную картину линий векторного поля Н в случае проводника с током, расположенного параллельно плоской поверхности парамагнетика.
Ответ:
12.17
2
Нарисовать примерную картину линий векторного поля B в случае проводника с током, расположенного параллельно плоской поверхности ферромагнетика.
Ответ:
13. Движение зарядов в электрических и магнитных полях
13.1.
1
Запишите уравнение движения нерелятивистской заряженной частицы в однородном магнитном поле с учетом действия сил радиационного трения.
Ответ:
13.2.
0
По какой траектории двигалась бы в общем случае нерелятивистская заряженная частица в однородном магнитном поле при отсутствии диссипативных сил?
Ответ:
13.3.
1
По какой траектории двигалась бы заряженная частица, влетающая в магнитное поле перпендикулярно его линиям, при наличии сил вязкого трения?
Ответ:
13.4.
2
При каких условиях заряженная частица, влетающая в постоянные взаимно перпендикулярные электрическое и магнитное поля Е и В будет продолжать двигаться равномерно и прямолинейно?
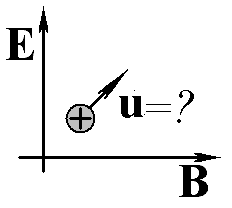
Ответ:
13.5.
2
Заряженная частица в начальный момент покоилась в скрещенных электрическом и магнитном полях Е и В. Нарисуйте примерную траекторию ее движения в случае E/B<<c.
Ответ:
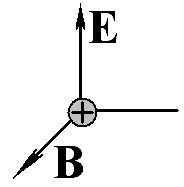
13.6.
1
На графике изображена зависимость от времени скорости нерелятивистской заряженной частицы в магнитном поле, разгоняемой вращающимся электрическим полем, циклическая частота которого совпадает с собственной частотой вращения заряженной частицы в магнитном поле. Радиационные потери энергии не учитываются. В тех же координатах нарисуйте примерный график зависимости скорости от времени в случае несовпадения указанных частот.
Ответ:
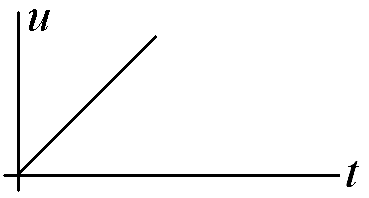
13.7.
1
На графике изображена зависимость от времени скорости нерелятивистской заряженной частицы в магнитном поле, разгоняемой вращающимся электрическим полем, циклическая частота которого совпадает с собственной частотой вращения заряженной частицы в магнитном поле. Радиационные потери энергии не учитываются. В тех же координатах нарисуйте примерный график зависимости скорости от времени , соответствующий учеты радиационных потерь.
Ответ:
13.8.
0
Запишите выражение для периода вращения нерелятивистской заряженной частицы (заряд q и масса m заданы) в однородном магнит ном поле B.
Решение:
Ответ:
13.9.
1
Запишите выражение для периода вращения релятивистской заряженной частицы (заряд q, масса покоя m и скорость u заданы) в однородном магнит ном поле B.
Решение:
Ответ:
13.10.
2
Нарисуйте примерную траекторию движения заряженной частицы, движущейся в перпендикулярное ее скорости магнитном поле, индукция которого возрастает в направлении, совпадающем с начальной скоростью частицы.
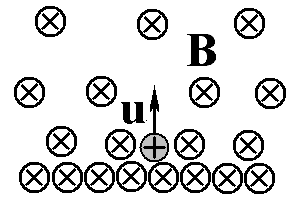
Ответ:
Закон электромагнитной индукции Фарадея
14.1.
0
Запишите выражение, связывающее ЭДС электромагнитной индукции Фараде в контуре я и магнитный поток, пронизывающий этот контур.
Ответ:
14.2.
0
Запишите уравнение системы Максвелла, представляющее в интегральной форме закон электромагнитной индукции Фарадея.
Ответ:
14.3.
0
Запишите уравнение системы Максвелла, представляющее в дифференциальной форме закон электромагнитной индукции Фарадея.
Ответ:
14.4.
0
Дайте определение индуктивности контура.
Ответ:
14.5.
0
Дайте определение коэффициента взаимной индукции двух контуров.
Ответ:
14.6.
0
Запишите выражение для ЭДС самоиндукции в контуре с индуктивностью L, ток в котором изменяется во времени по известному закону I(t).
Ответ:
14.7.
1
Запишите общее выражение для индуктивности контура заданной формы
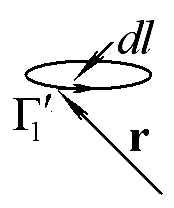
Ответ:
14.8.
1
Запишите общее выражение для коэффициента взаимной индукции двух контуров заданной формы
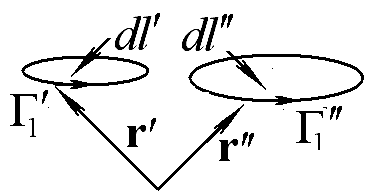
Ответ:
14.8.
1
Найдите индуктивность катушки из N витков, намотанный на цилиндр длиной h с площадью поперечного сечения S, сделанного из материала с магнитной проницаемостью μ.
Ответ:
14.9.
1
Найдите коэффициент взаимной индукции двух катушек, содержащих N1 и N2 витков соответственно, намотанных на цилиндр длиной h с площадью поперечного сечения S, сделанного из материала с магнитной проницаемостью μ.
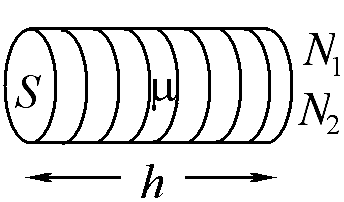
Ответ:
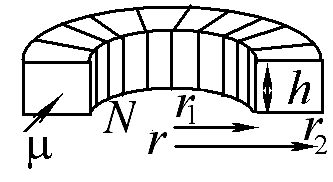
14.10
2
Найдите индуктивность катушки из N витков, намотанной на кольцевой сердечник с прямоугольным сечением. Все геометрические размеры сердечника и магнитная проницаемость его материала заданы.
Ответ:
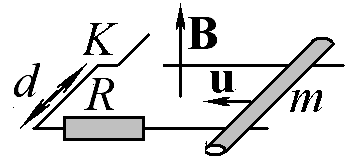
14.11.
2
Запишите дифференциальное уравнение, описывающее движение стержня после замыкания ключа K. Сопротивление проводов и стержня мало Трения нет.
Ответ:
14.12.
1
В каком направлении потечет электрический ток в контуре при движении постоянного магнита? (показать стрелкой и объяснить).
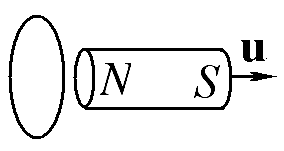
Объяснение:
14.13
1
В каком направлении потечет электрический ток в контуре при движении постоянного магнита? (показать стрелкой и объяснить).
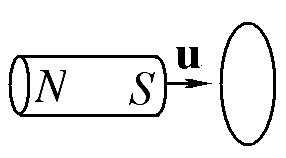
Объяснение:
14.14
1
В каком направлении потечет электрический ток в контуре при замыкании ключа?
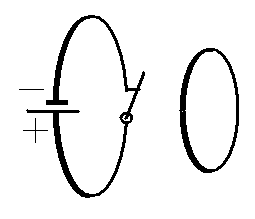
Объяснение:
14.15
0
Запишите выражение для объемной плотности энергии магнитного поля в вакууме.
Ответ:
14.16
0
Запишите выражение для объемной плотности энергии магнитного поля в магнетике с магнитной проницаемостью μ.
Ответ:
14.17.
2
В некотором объеме V, заполненном однородным анизотропным магнетиком с заданной магнитной проницаемостью μ, создано однородное магнитное поле с индукцией В. Рассчитайте энергию, запасенную в объеме.
;
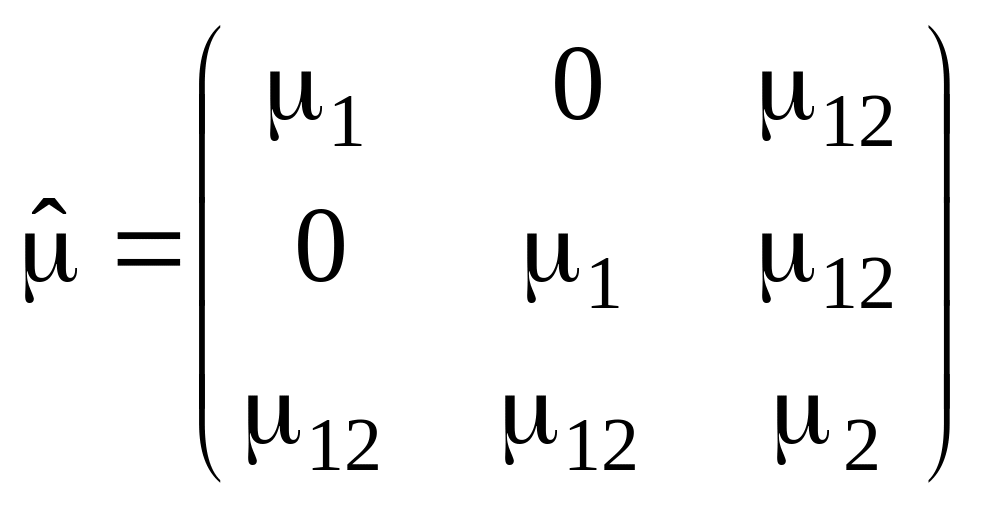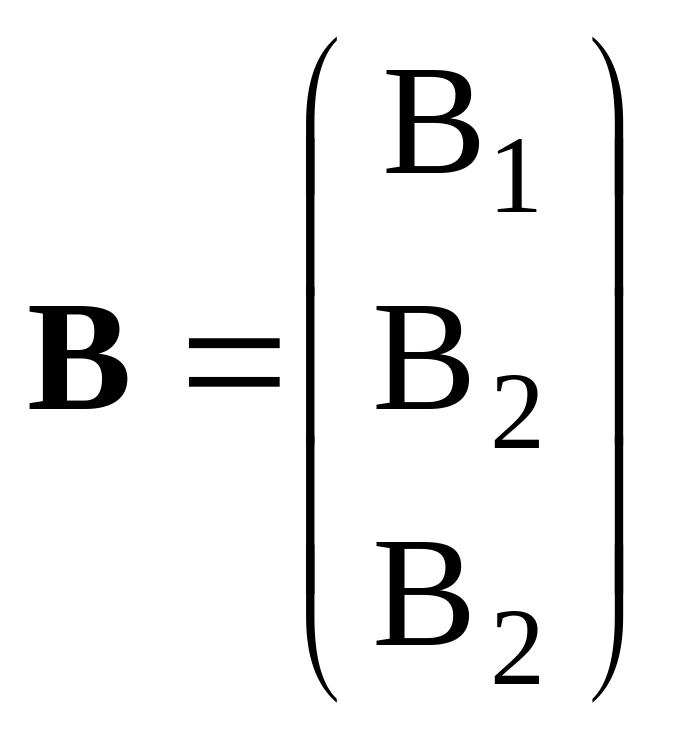
Ответ:
14.18.
1
Рассчитайте энергию, запасенную в объеме соленоида, содержащего N витков с током I, намотанных на цилиндрический сердечник заданных размеров, сделанный из однородного изотропного магнетика с проницаемостью μ.
Ответ:
Переменный электрический ток
15.1.
1
Запишите дифференциальное уравнение, описывающее изменение во времени напряжения на конденсаторе, включенном в изображенную на рисунке цепь.
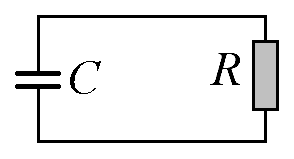
Ответ:
15.2.
1
Нарисуйте примерный график зависимости от времени напряжения на конденсаторе, включенном в изображенную на рисунке цепь. В начальный момент напряжение равнялось u0.
Ответ:
15.3.
1
Запишите дифференциальное уравнение, описывающее изменение во времени тока в изображенной на рисунке цепи.
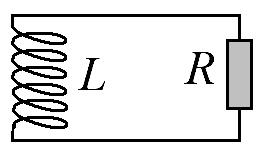
Ответ:
15.4.
1
Нарисуйте примерный график зависимости от времени силы тока в изображенную на рисунке цепи. В начальный момент сила тока равнялось I0.
Ответ:
15.5.
0
Запишите дифференциальное уравнение, описывающее изменение во времени тока в изображенной на рисунке цепи.
Ответ:
15.6.
0
На графике представлен вид зависимости от времени заряда на конденсаторе в случае идеального колебательного контура (R = 0). В тех же координатах изобразите график зависимости u(t) в случае затухающих колебаний (β<ω0).
Ответ:
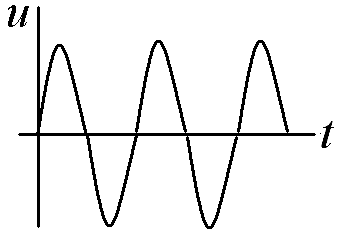
15.7.
1
На графике представлен вид зависимости от времени заряда на конденсаторе в случае идеального колебательного контура (R = 0). В тех же координатах изобразите график зависимости u(t) в случае апериодического режима работы колебательного контура (β>ω0).
Ответ:
15.8.
1
Запишите общее решение однородного дифференциального уравнения, описывающего электрические колебания в реальном контуре в случае вырожденных корней характеристического уравнения.
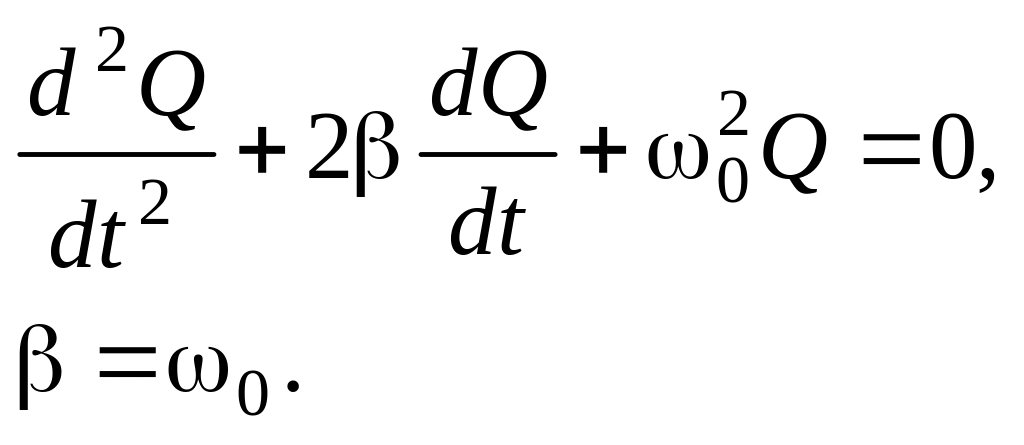
Ответ:
15.9.
1
В комплексном представлении гармонический сигнал u(t) имеет вид, представленный приведенной формулой. Записать выражение для импеданса конденсатора с емкостью С.
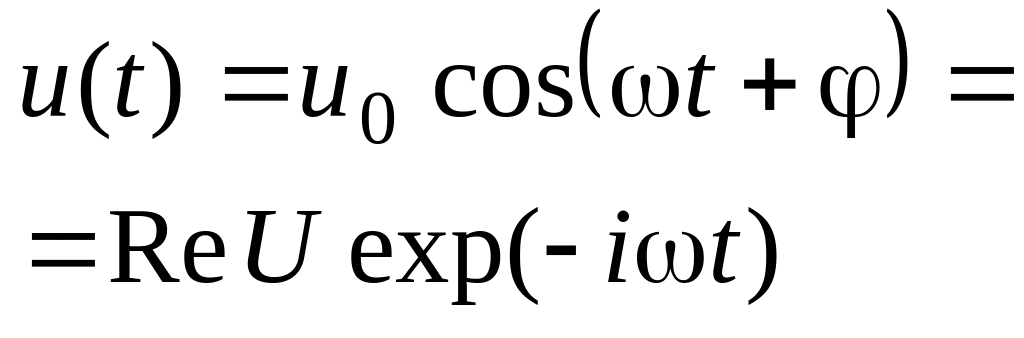
Ответ:
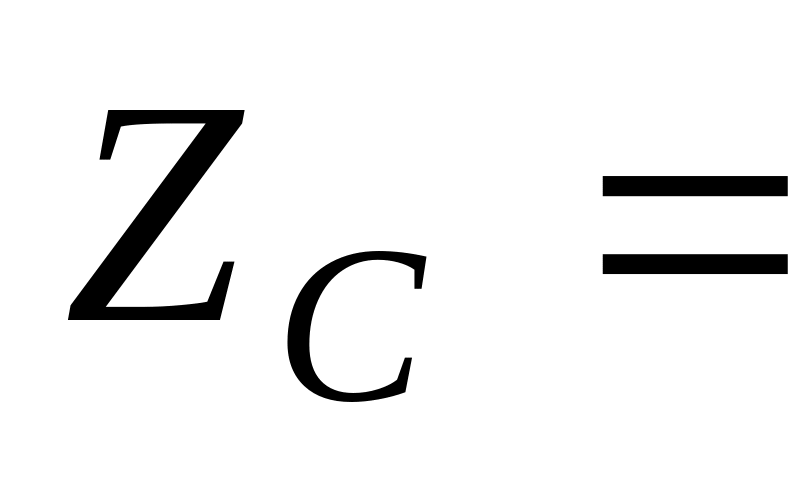
15.10.
1
В комплексном представлении гармонический сигнал u(t) имеет вид, представленный приведенной формулой. Записать выражение для импеданса катушки с индуктивностью L.
Ответ:
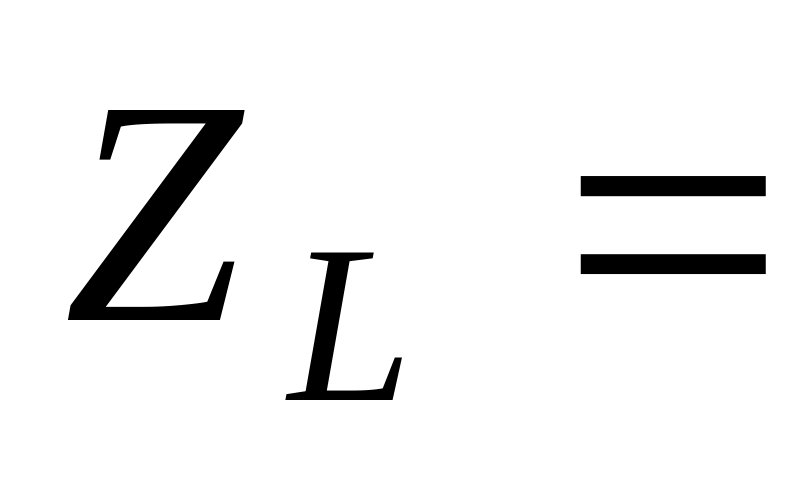
15.11.
1
Какую величину принято называть волновым сопротивлением коаксиального кабеля?
Ответ:
Система уравнений Максвелла
16.1.
0
Запишите выражение для введенного Максвеллом тока смещения в вакууме.
Ответ:
16.2.
0
Запишите полную систему уравнений Максвелла для электромагнитного поля в вакууме (в дифференциальной форме).
Ответ:
16.3.
1
Запишите полную систему уравнений Максвелла для электромагнитного поля в вакууме (в интегральной форме).
Ответ:
16.4.
0
Запишите полную систему уравнений Максвелла для вещества (в дифференциальной форме).
Ответ:
16.5.
1
Запишите полную систему уравнений Максвелла для вещества (в интегральной форме).
Ответ:
16.6.
0
Запишите общее выражение для плотности потока энергии электромагнитного поля в вакууме.
Ответ:
16.7.
1
Запишите общее выражение для плотности потока энергии электромагнитного поля в веществе.
Ответ:
16.8.
0
Запишите закон сохранения энергии для электромагнитного поля в дифференциальной форме
Ответ:
16.9.
0
Запишите закон сохранения энергии для электромагнитного поля в интегральной форме.
Ответ:
16.10.
2
Укажите направления для векторов E, B и S в точке О для случая источника с постоянной ЭДС, подключенного к активной нагрузке двумя длинными цилиндрическими проводами с малым сопротивлением.
Ответ:
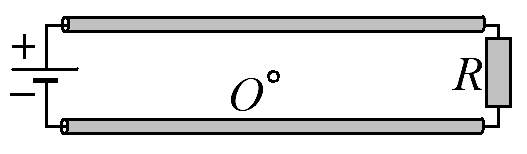
16.11.
1
Укажите направления для векторов E, B и S в точке О для случая состоящего из двух круговых дисков плоского конденсатора, заряжаемого постоянным током I.
Ответ:
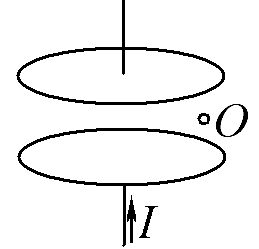
16.12.
2
Укажите направления для векторов E, B и S в точке О для случая постоянного магнита в форме цилиндра, несущего равномерно распределенный по поверхности положительный электрический заряд.
Ответ:
16.13.
0
Запишите однородное уравнение Д’Аламбера для электромагнитных волн в двухпроводной линии, токоведущие части которой расположены в вакууме.
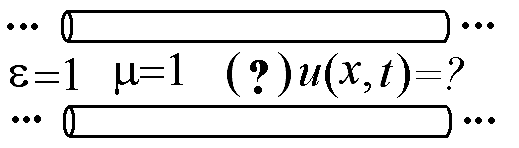
Ответ:
16.14.
1
Запишите однородное уравнение Д’Аламбера для электромагнитных волн в двухпроводной линии, токоведущие части которой расположены в веществе с заданными свойствами.
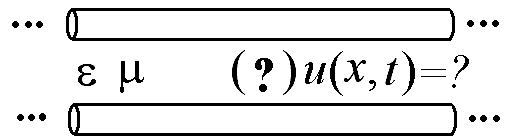
Ответ:
16.15.
0
Запишите общее решение однородного уравнения Д’Аламбера для электромагнитных волн в двухпроводной линии, токоведущие части которой расположены в веществе с заданными свойствами.
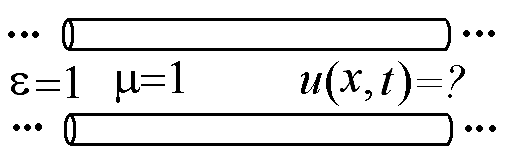
Ответ:
16.16.
1
Запишите общее решение однородного уравнения для электромагнитных волн в двухпроводной линии, токоведущие части которой расположены в веществе с заданными свойствами.
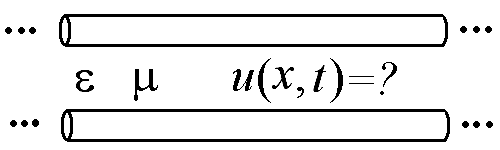
Ответ:
16.17.
0
Запишите однородное уравнение Д’Аламбера для электромагнитных волн в пустом пространстве.
Ответ:
16.18.
1
Запишите однородное уравнение Д’Аламбера для электромагнитных волн в веществе с заданными ε и μ.
Ответ:
16.19.
0
Запишите допустимое решение (в наиболее общем воде) уравнения Д’Аламбера для плоских монохроматических волн в вакууме.
Ответ:
16.20.
1
Запишите допустимое решение (в наиболее общем воде) уравнения Д’Аламбера для плоских монохроматических волн в веществе с заданными ε и μ..
Ответ:
16.21.
0
При выполнении каких условий для волнового вектора k в вакууме могут существовать плоские монохроматические волны?
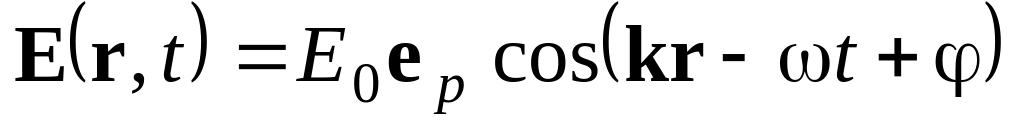
Ответ:
16.22.
1
При выполнении каких условий для волнового вектора k в веществе с ε=const и μ=const могут существовать плоские монохроматические волны?
.
Ответ:
17*. Электродинамика в релятивистских обозначениях
17.1.
1
Запишите явное выражение для четырехвектора скорости.
Ответ:
17.2.
0
Запишите явное выражение для четырехвектора импульса.
Ответ:
17.3.
0
Запишите явное выражение для квадрата четырехвектора импульса.
Ответ:
17.4.
1
Запишите выражение, связывающее четырехвектор импульса с четырехвектором силы.
Ответ:
17.5.
0
Запишите преобразования Лоренца для компонент четырехвектора aζ.
Ответ:
17.5.
1
Запишите явное выражение для четырехмерного оператора набла.
Ответ:
17.6
2
С помощью четырехмерного оператора набла запишите явное выражение для приращения скалярной функции, аргументом которой является четырехвектор.
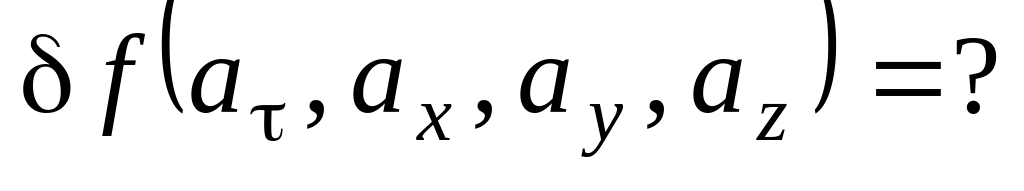
Ответ:
17.7.
1
Запишите в явном виде выражение для «четырехдивергениции» четурехвектора.
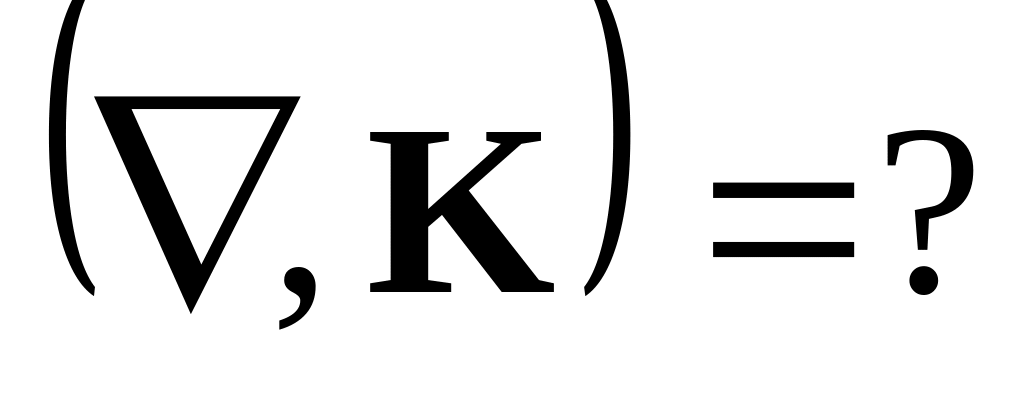
Ответ:
17.8.
1
Дайте определение четырехвектора плотности тока и запишите явное выражение его компонент через составляющие трехмерной плотности тока и плотность электрического заряда
Ответ:
17.9.
1
Запишите закон сохранения электрического заряда, используя четырехмерные обозначения.
Ответ:
Вопросы для коллоквиума и экзамена
Экзамен (и коллоквиум) по направлению Прикладные математика и физика проводятся в устной форме. Использование студентами конспектов и какой-либо справочной литературы на экзамене не допускается. Программа коллоквиума соответствует материалу лекций 1-8. Программа экзамена соответствует темам лекций 9-18, а так же включает вопросы обязательного минимума по лекциям 1-8.
Студенты, прослушавшие курс «Электричество и магнетизм», должны быть готовы к изложению материала по вопросам обязательного минимума без какой-либо предварительной подготовки. Неспособность студента поддержать беседу по любому из указанных вопросов означает невозможность получения им положительной оценки на экзамене или коллоквиуме вне зависимости от ответов на вопросы билета. Проводящие опрос студентов преподаватели обязаны убедиться в способности студента дать вразумительные ответы по 2-3 вопросам обязательного минимума. Знание обязательного минимума является необходимым, но не достаточным условием получения положительной оценки на экзамене или коллоквиуме.
Предлагаемые на коллоквиуме и экзамене билеты содержат по два вопроса из списков, приведенных в настоящем пособии. При подготовке студент должен оформить лист устного ответа, который должен содержать основные положения ответа на вопросы билета, необходимые рисунки и формулы с их выводами.
В ходе опроса преподаватель имеет право задавать любые дополнительные вопросы из программы коллоквиума или экзамена, а так же – уточняющие вопросы по математике, в рамках разделов, необходимых для изложения вопросов экзаменационного билета. В качестве дополнительных вопросов так же могут использоваться задачи по курсу из списка, приведенного в настоящем пособии. Все задаваемые дополнительные вопросы преподаватель должен фиксироваться на листе устного ответа студента.
Проводящим опрос преподавателям предоставляется информация о результатах, показанных студентами на контрольных и теоретических тестах. При необходимости в ходе опроса преподаватель может ознакомиться с соответствующими работами студента. В случае возникновения существенных расхождений между предполагаемой оценкой за экзамен (или коллоквиум) и результатами внутри семестровой аттестации (контрольных работ и/или тестов), преподавателю рекомендуется задать несколько дополнительных вопросов по темам, ранее вызвавшим затруднения у сдающего экзамен студента. Выставляемая на экзамене (коллоквиуме) оценка должна отражать знания студента на момент сдачи экзамена (коллоквиума), а не его промежуточные результаты, показанные во время обучения. Оценки за коллоквиум и экзамен выставляются по десятибальной шкале.
Преподаватель обязан объявить студенту его оценки и записать ее на экзаменационный лист до ее проставления в зачетную книжку и экзаменационную ведомость. В случае несогласия с выставляемой ему оценкой студент должен информировать об этом преподавателя до момента ее проставления в ведомость и зачетную книжку. В этом случае студенту предоставляется право дополнить лист своего ответа по основным и дополнительным вопросам в присутствии проводившего опрос преподавателя. Если внесенные студентом дополнения не повлияли не решение преподавателя, а студент продолжает настаивать на изменении его оценки, решение по этому вопросу принимается комиссией, в состав которой входит читавший курс лектор, заведующий обеспечивающей преподавание курса кафедрой и представитель деканата. Комиссия принимает решение только на основании информации, содержащейся на листе ответа студента. Решение комиссии принимается до окончания экзаменационной сессии, является окончательным и не подлежит обжалованию на уровне администрации кафедры и факультета.
Оценка 10 (5+) выставляется студенту в исключительных случаях, когда его ответ содержал оригинальный подход к изложению материала или содержал дополнительные сведения, существенно выходящую за рамки программы курса. Претензии студентов в отношении не выставления им указанной оценки не принимаются, комиссии по этим случаям не создаются.
Все листы ответов студентов с выставленными оценками и подписями преподавателей вместе с результатами промежуточных внутри семестровых аттестаций сохраняются до окончания дополнительной экзаменационной сессии. Деканат, руководство обеспечивающей преподавание курса кафедры и методическая комиссия факультета могут использовать эти материалы для проверки качества обучения студентов и разработке рекомендации для дальнейшего совершенствования преподавания курса.
Для студентов, набравших высокий рейтинг по результатам коллоквиума и внутрисеместровых аттестаций при условии получения ими всех зачетов может быть организована досрочная сдача экзамена. Для проведения досрочного экзамена создается дополнительная ведомость, в которую заносятся все выставленные студентам оценки, в том числе – неудовлетворительные. В день проведения основного экзамена все оценки из указанной ведомости (включая неудовлетворительные) переносятся в основную ведомость. Пересдача досрочного экзамена во время основной сессии не допускается. В исключительных случаях в случае получения на досрочном экзамене положительной, но не удовлетворяющей студента оценки (не ниже 5 по десятибалльной шкале) декан имеет право в индивидуальном порядке аннулировать результат досрочной сдачи экзамена и допустить студента к сдаче основного экзамена в соответствии с расписанием.