3.Решение интегральных уравнений Фредгольма II рода с вырожденными ядрами. Метод констант.

ЯФ , представимое в виде , называется вырожденным. ИУФ II рода с вырожденным ядром

, или в более удобном виде,

(3.1) и система алгебраических уравнений , к которой приводится это уравнение, где , , , , , , ─ единичная матрица, одновременно разрешимы или не разрешимы. Решением этой системы являются константы , вычислив которые, мы, в силу (3.1) найдем решение данного ИУ. Возможны следующие два случая:

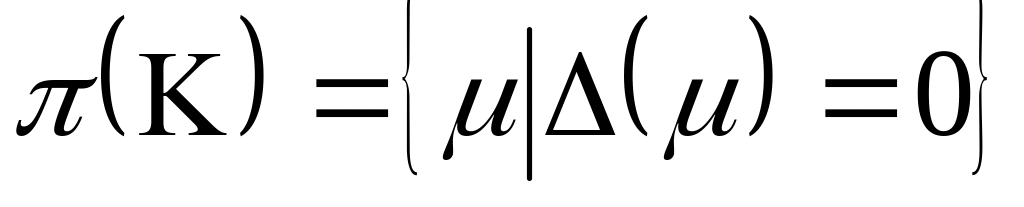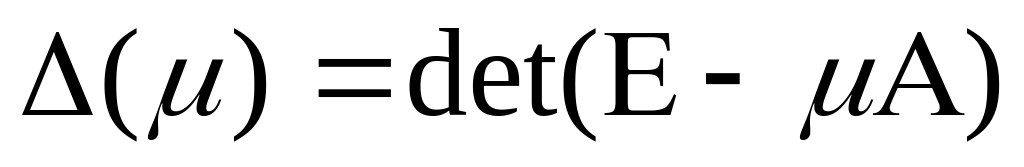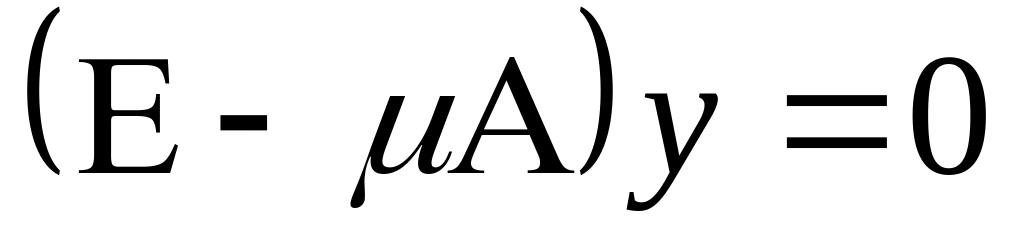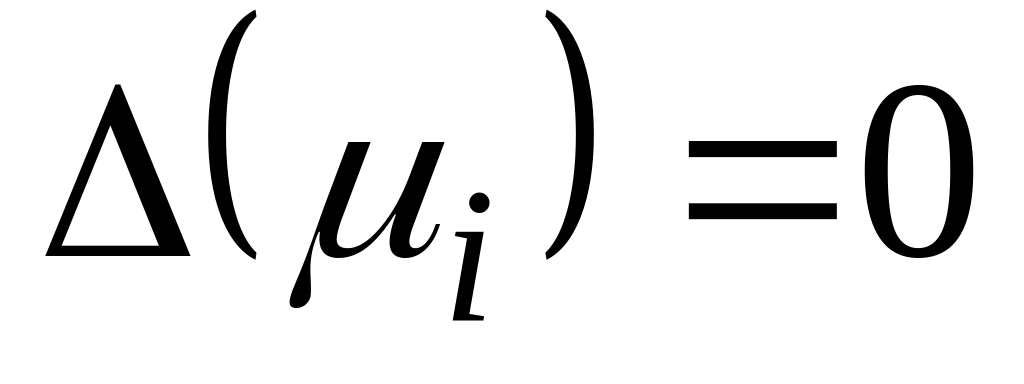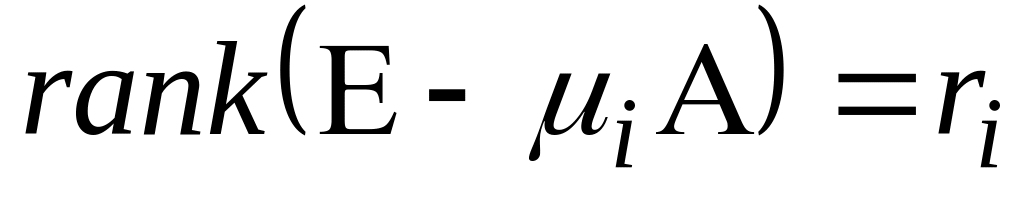1. уравнение (3.1) - однородное, т.е. необходимо найти его ХЧ и СФ. В этом случае ,где , т. к. для этих и только этих соответствующая система имеет нетривиальное решение. Если и , то 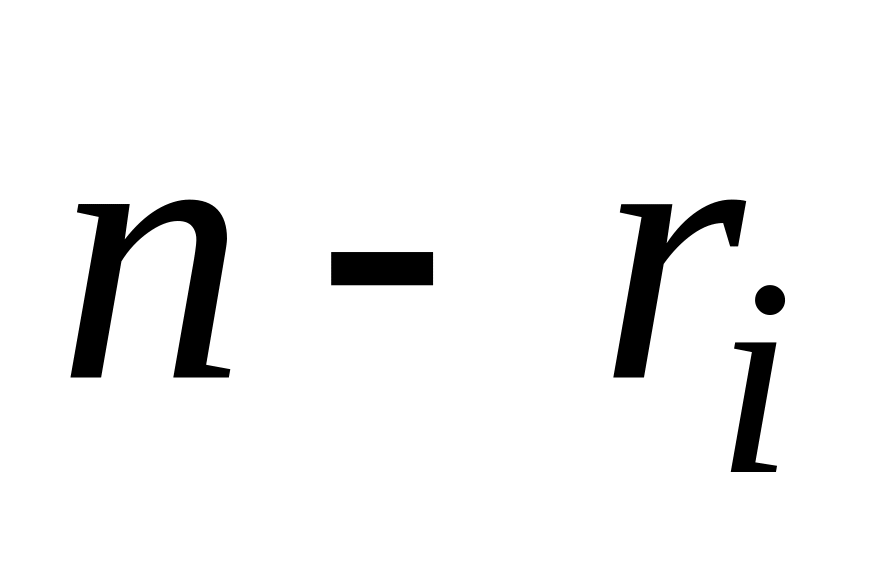- кратность ХЧ

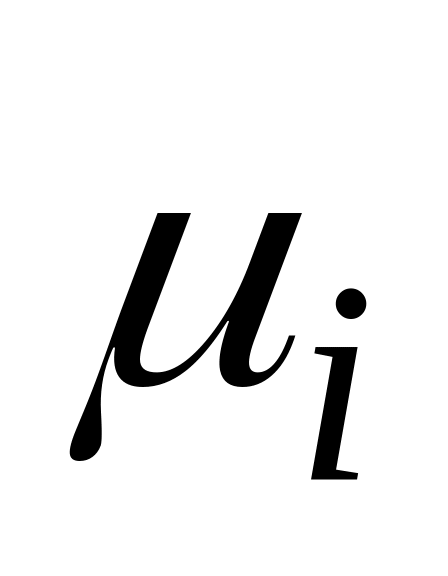
2. уравнение (3.1) – неоднородное. Решая систему уравнений 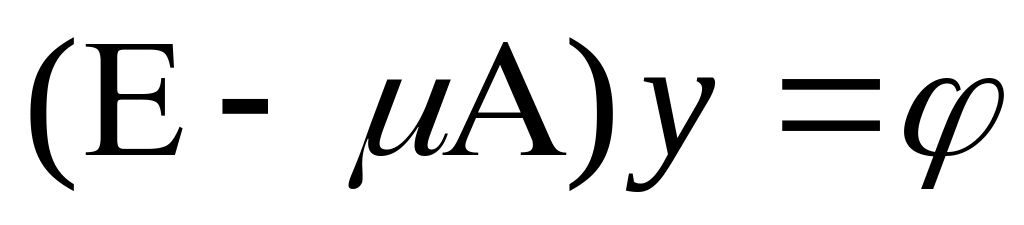, например, по формулам Крамера, находим 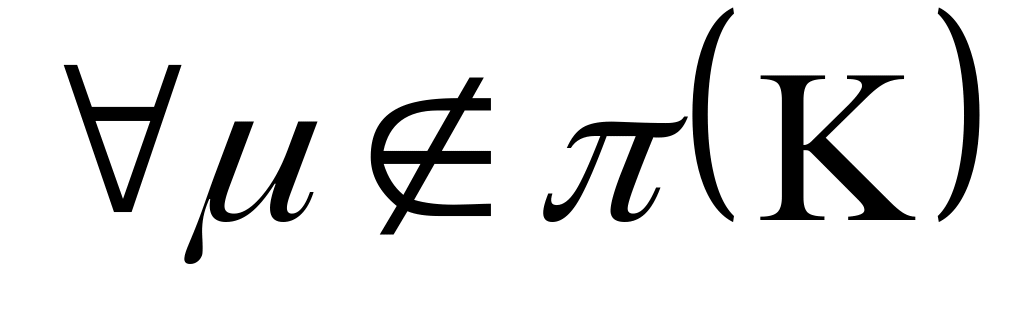единственное её решение, а, следовательно, и единственное решение ИУ (3.1). Далее необходимо исследовать систему для каждого 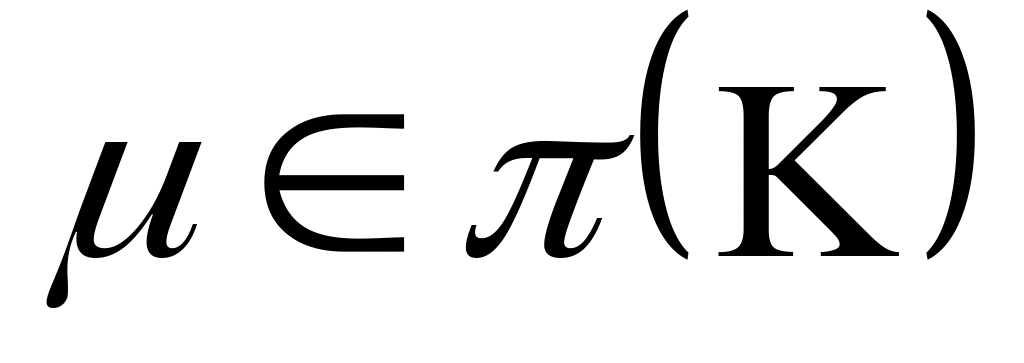. В этих случаях система может быть совместной и неопределённой или несовместной. В первом случае ИУ (3.1) имеет бесконечное множество решений, во втором – ИУ (3.1) не разрешимо.

Пример 3.1. Решить ИУ

.

Решение. Раскроем скобки

, откуда

, (3.2)

где

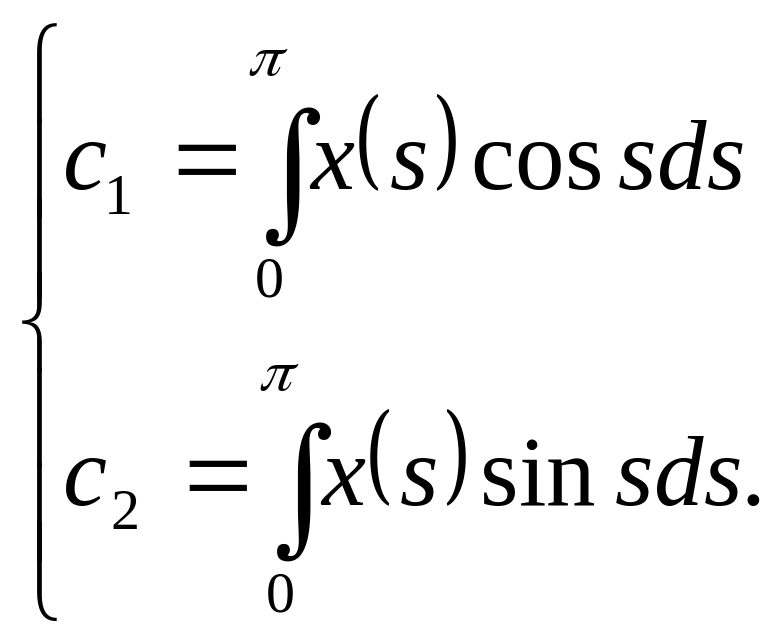
Подставляя (3.2) в систему и приводя подобные, получим

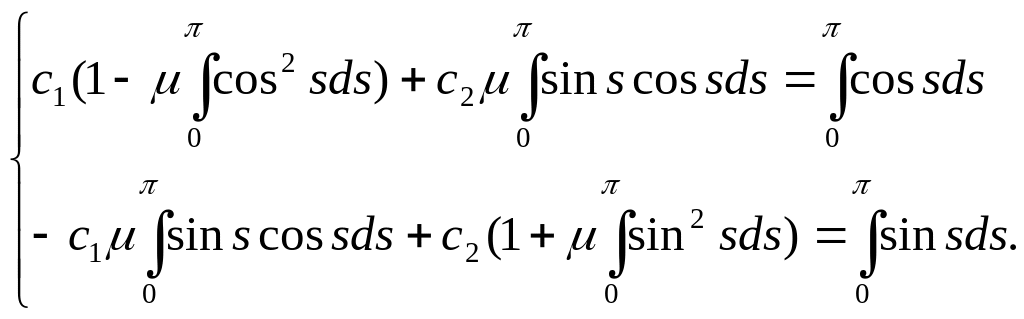
Вычислив интегралы, приходим к системе

(3.3)

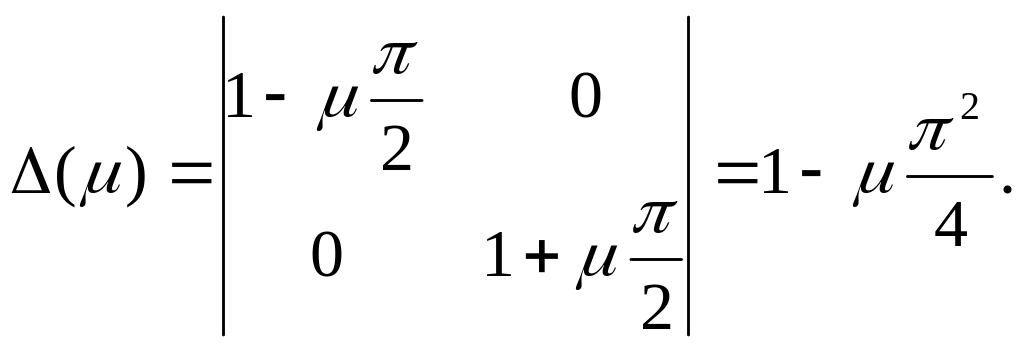
а) . Данная система имеет единственное решение

и из (3.2) находим решение ИУ

б) . Подставляя в систему (3.3), получим

. В этом случае ИУ имеет бесконечное множество решений , где - произвольная константа.

в) . Подставим в систему (3.3):

Данная система не имеет решений.

Таким образом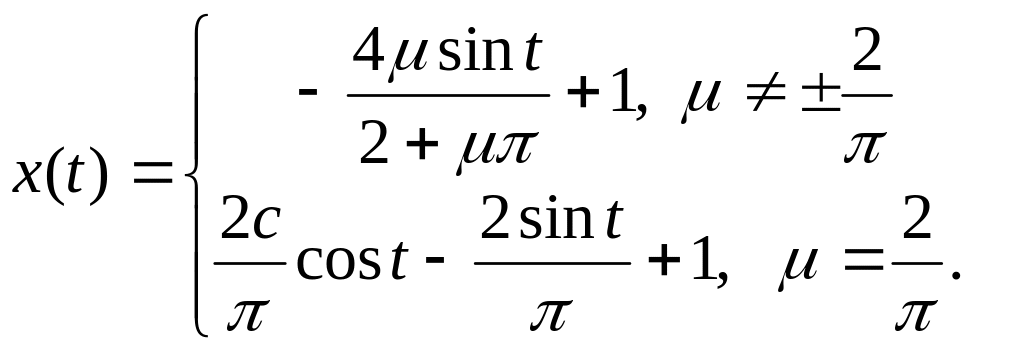

При ИУ не разрешимо.

Пример3.2. Найти ХЧ и СФ уравнения .

Решение. Применяя метод констант и используя вычисления из примера 3.3, приходим к следующим соотношениям:

(3.4)

- ХЧ уравнения. Найдем нетривиальные решения системы (3.4) при :

. Вычислим ранг матрицы данной системы: , отсюда -ХЧ кратности 2. Найдем фундаментальную систему решений с помощью таблицы:

	0
0

Т.о. -ХЧ уравнения, - СФ уравнения.

Пример3.3. Найти ХЧ и СФ уравнения .

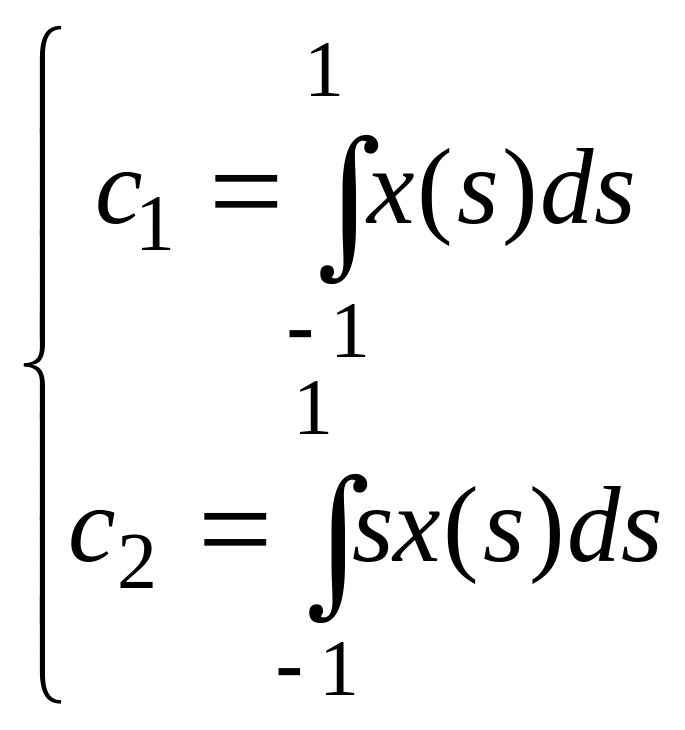Решение. Т.к. (3.5), где , то 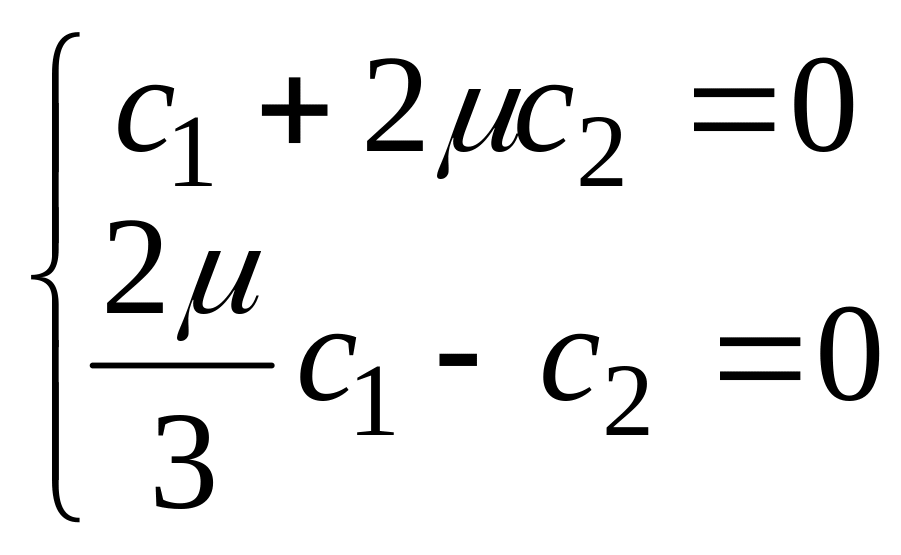; . - ХЧ уравнения. Подставляя в систему, приходим квыводу, что ранг матриц полученных систем равен 1 и, поэтому для нахождения общего решения достаточно из любого уравнения системы 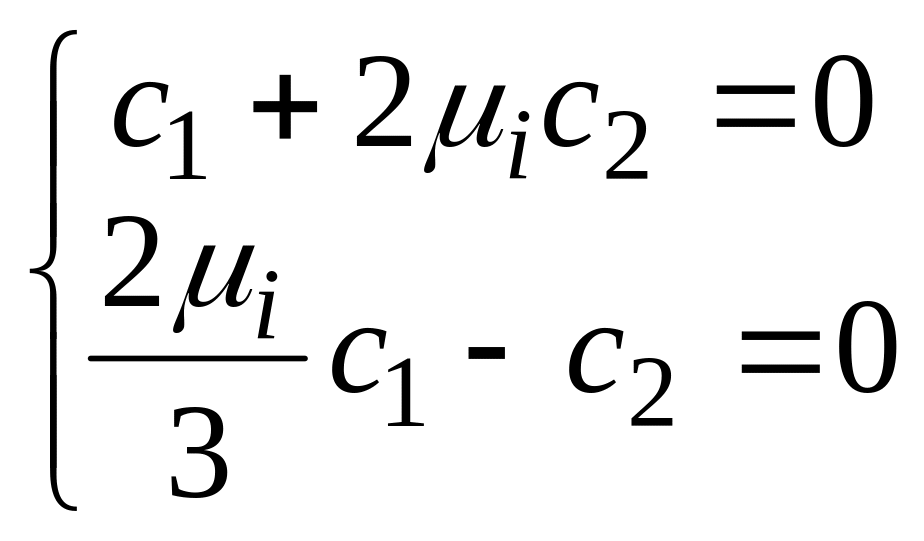выразить одну неизвестную через другую, например, .

Подставляя в (3.5), найдем СФ уравнения :

.

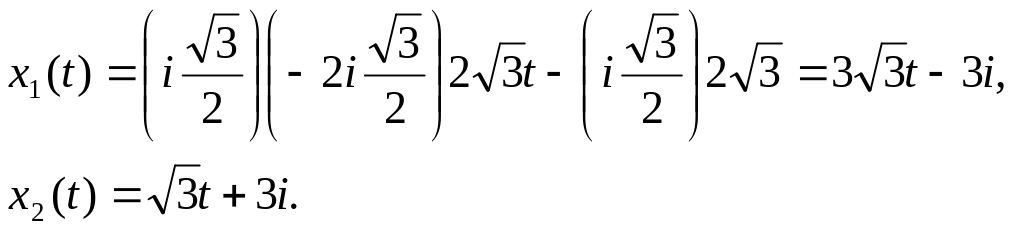Таким образом,

- ХЧ, а , - СФ данного ИУ.

Упражнения. 1) Решить неоднородные ИУФ II рода(см. табл..3.1):

Таблица 3.1:

N п\п				N п/п
3.1				3.8
3.2				3.9
3.3				3. 10
3.4				3. 11
3.5				3. 12
3.6				3. 13
3.7				3. 14

2) Найти ХЧ и СФ соответствующих однородных ИУ. (см. табл 3.2):

Таблица 3.2

N п\п			N п\п
3.15			3.23
3.16			3.24
3.17			3.25
3.18			3.26
3.19			3.27
3.20			3.28
3.21			3.29
3.22			3.30