
- •Введение
- •Список кратких обозначений
- •1.Предварительные сведения. Классификация интегральных уравнений.
- •2. Метод итерированных ядер (малого параметра) для решения неоднородного интегрального уравнения Фредгольма и интегрального уравнения Вольтерра II рода.
- •3.Решение интегральных уравнений Фредгольма II рода с вырожденными ядрами. Метод констант.
- •4.Однородные интегральные уравнения Фредгольма II рода с симметрическими ядрами (ся).
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ТАВРИЧЕСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
им. В.И. ВЕРНАДСКОГО
Кафедра алгебры и функционального анализа
Третьяков Д.В.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ДЛЯ РЕШЕНИЯ ЗАДАЧ ПО КУРСУ
« ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ »
(часть I)
для студентов III и IV курсов дневной и заочной форм обучения
и экстерната специальностей 6.080100 «математика»,
6.080200 «прикладная математика», «информатика»
учебно-квалификационного уровня «бакалавр»
профессиональных направлений подготовки
0801 «математика» и 0802 «прикладная математика»
Симферополь 2004
Печатается по решению научно –
методического совета ТНУ
от 28.03.03
Введение
В методических указаниях рассмотрены основные методы решений интегральных уравнений Фредгольма и Вольтерра, предусмотренные университетской программой. Указания состоят из 10 разделов, каждый из которых содержит небольшой теоретический обзор по данной теме, решения типовых задач и заданий для самостоятельного выполнения. Для удобства весь текст методических указаний разбит на 3 части. Первая часть содержит следующие темы:
1. Предварительные сведения. Классификация интегральных уравнений.
2. Метод итерированных ядер (малого параметра)для решения неоднородных интегральных уравнений Фредгольма и Вольтерра II рода.
3. Решение интегральных уравнений Фредгольма II рода с вырожденными ядрами (метод констант).
4. Однородные интегральные уравнения Фредгольма II рода с симметрическими ядрами.
В каждой части пособия приведен также список кратких обозначений.
Набор текста пособия производили Кирюшкина, С.Н. Сарачева А. С. и Лебедева Е. В.
Список кратких обозначений
ИПЛ – интегральное преобразование Лапласа;
ИУ – интегральное уравнение;
ИУВ – ИУ Вольтерра;
ИУФ – ИУ Фредгольма;
ОВ – оператор Вольтерра;
РЯФ – резольвентное ядро Фредгольма;
СФ – собственная функция;
ХЧ – характеристическое число;
СЯ – симметрическое ядро;
ЯВ – ядро Вольтерра;
ЯФ – ядро Фредгольма.
1.Предварительные сведения. Классификация интегральных уравнений.
Пустьa,bR, (a<b) – фиксированные числа, D=[a,b][a,b] (в частности, может быть, что a = - или b = ).
Пусть L2(D)- гильбертово пространство со скалярным произведением
![]()
![]()
и нормой
![]() .
Любой элемент KL2(D)
называется ядром Фредгольма (ЯФ). Ядро
вида
.
Любой элемент KL2(D)
называется ядром Фредгольма (ЯФ). Ядро
вида
![]() называется произведением ЯФ. Так как
называется произведением ЯФ. Так как
![]() ,
то
,
то
![]() и
и
![]() - ЯФ.
- ЯФ.
Последовательность ЯФ K1=K
, K2= K1K
,…, Kn=Kn-1K
,…называется последовательностью
итерированных ядер для ЯФ K,
![]() (nN).
(nN).
Ядро Вольтерра (ЯВ) – это ЯФ , равное нулю или при t < s или при t < s . ЯВ V1 и V2 называются однотипными , если V1= V2 = 0 или при t < s или при t > s. Произведение однотипных ЯВ (например, равных нулю при t < s ) вычисляется по формуле
![]() .
.
Оператор вида
![]() ,
К ─ ЯФ,
,
К ─ ЯФ,
x
L2[a,b],
называется оператором Фредгольма (ОФ).
Если K – ОФ с ЯФ K,
то KL(L2[a,b])
и
![]() .
Пусть K и L
– ОФ с ЯФ K и L
соответственно. Тогда KL
и LK –ОФ с ЯФ KL
и LK
. Отсюда Kn
– ОФ с ЯФ Kn
(n ÎN
). Оператор K* также
является ОФ с ЯФ K*
(
.
Пусть K и L
– ОФ с ЯФ K и L
соответственно. Тогда KL
и LK –ОФ с ЯФ KL
и LK
. Отсюда Kn
– ОФ с ЯФ Kn
(n ÎN
). Оператор K* также
является ОФ с ЯФ K*
(![]() сопряженное ЯФ,
сопряженное ЯФ,
![]() ).
Аналогичными свойствами обладает
оператор Вольтерра (ОВ):
).
Аналогичными свойствами обладает
оператор Вольтерра (ОВ):
![]() .
(1.1) Подробнее
см. в [ 1,2,5,6] .
.
(1.1) Подробнее
см. в [ 1,2,5,6] .
Интегральное уравнение вида
![]() называется неоднородным (однородным,
если f = 0) интегральным
уравнением Фредгольма (ИУФ) II
рода (K - ЯФ, f
L2[a,b]
- известная функция ,
называется неоднородным (однородным,
если f = 0) интегральным
уравнением Фредгольма (ИУФ) II
рода (K - ЯФ, f
L2[a,b]
- известная функция ,
![]() C-
параметр).
C-
параметр).
Уравнение вида
![]() – неоднородное (однородное, если f
= 0) интегральное уравнение Вольтерра
(ИУВ) II рода,
– неоднородное (однородное, если f
= 0) интегральное уравнение Вольтерра
(ИУВ) II рода,
![]() - ИУФ I рода,
- ИУФ I рода,
![]() -ИУВ II рода.
-ИУВ II рода.
Число
![]()
![]() называется характеристическим числом
(ХЧ) интегрального оператора
называется характеристическим числом
(ХЧ) интегрального оператора
![]() (понятие ХЧ так же определяется и для
произвольного ограниченного оператора),
если уравнение
(понятие ХЧ так же определяется и для
произвольного ограниченного оператора),
если уравнение
![]() имеет нетривиальное решение. Любое
нетривиальное решение этого уравнения
называется собственной функцией
(СФ)
оператора
,
отвечающей ХЧ
имеет нетривиальное решение. Любое
нетривиальное решение этого уравнения
называется собственной функцией
(СФ)
оператора
,
отвечающей ХЧ
![]() ,
а число
,
а число
![]() называется кратностью ХЧ
.
Множество всех ХЧ оператора
обозначают через
называется кратностью ХЧ
.
Множество всех ХЧ оператора
обозначают через
![]() .
Перечислим основные свойства множества
,
вытекающие непосредственно из
определения:
.
Перечислим основные свойства множества
,
вытекающие непосредственно из
определения:
1)
![]() для любого оператора
;
для любого оператора
;
2)![]() ;
;
3)![]() .
.
Упражнения.
Пусть V1 ,V2 – однотипные ЯВ (обращаются в 0 при t>s).Найти V1 V2.
Положим D= [-a,a] [-a,a] .Пусть V1 ,V2 L2(D) и V1 =V2=0 при |s|>|t| (при |s|<|t|) .Найти V1 V2.
Найти сопряженные операторы V* (см.(1.1)) и V1*, где
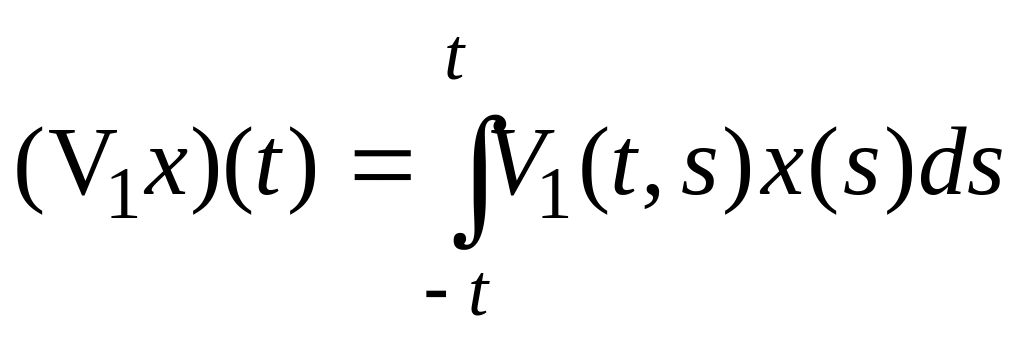 ,
x
L2[-a,a].
,
x
L2[-a,a].Пусть
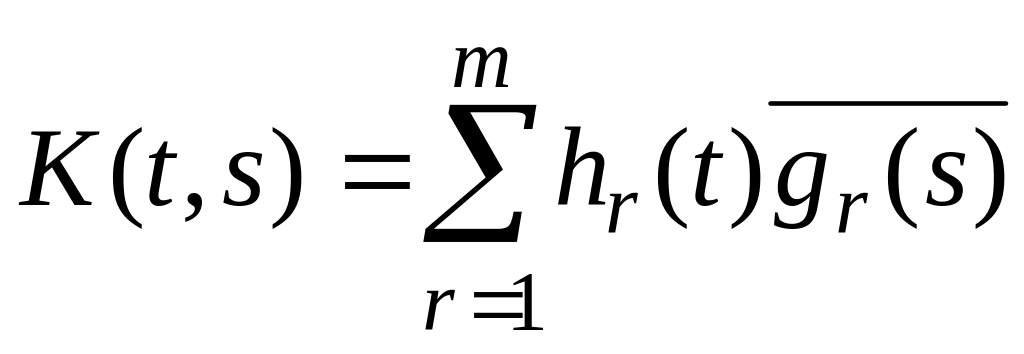 ,
,
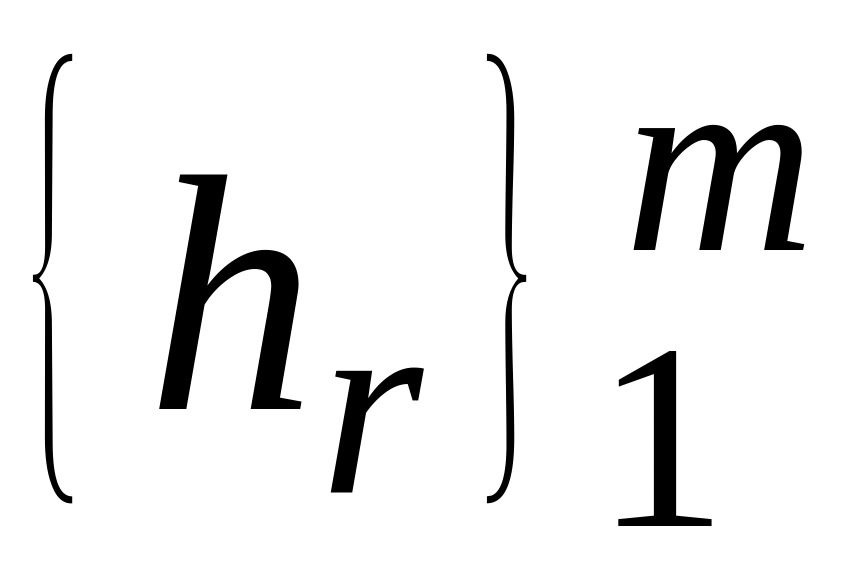
L2[a,b]
,
L2[a,b]
,
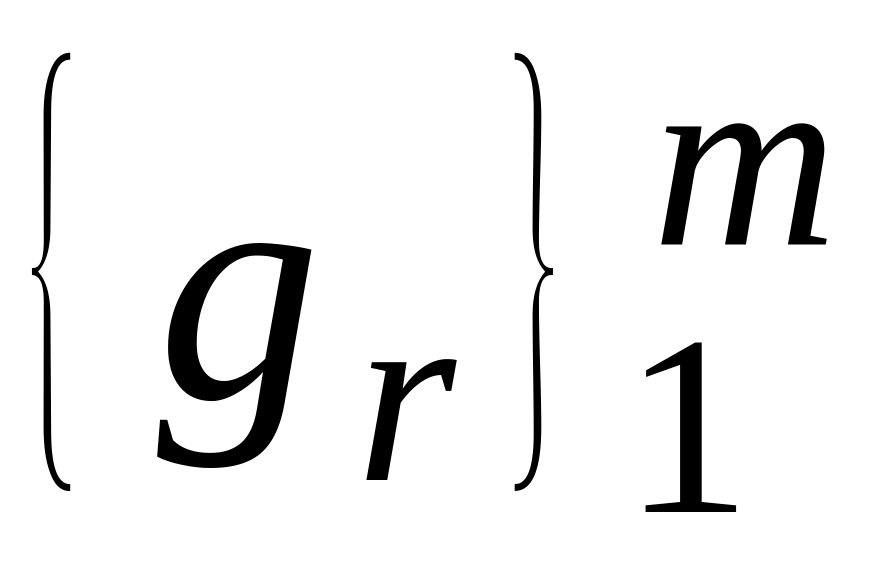
L2[a,b]
– ЯФ (mN-фиксировано).
Найти формулу для вычисления Kn(t,s)
, n N.
L2[a,b]
– ЯФ (mN-фиксировано).
Найти формулу для вычисления Kn(t,s)
, n N.Получить расчетные формулы для
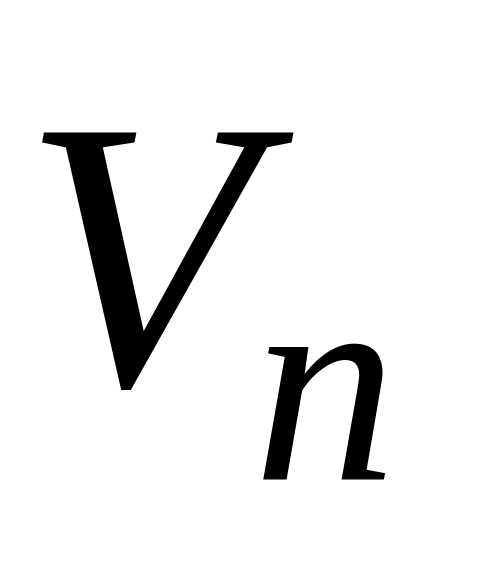 в случае ИУВ
в случае ИУВ
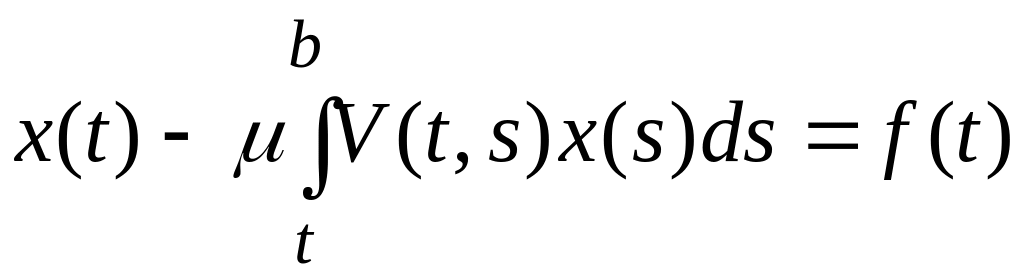 .
.
