4.2 Уточнение размеров поперечного сечения

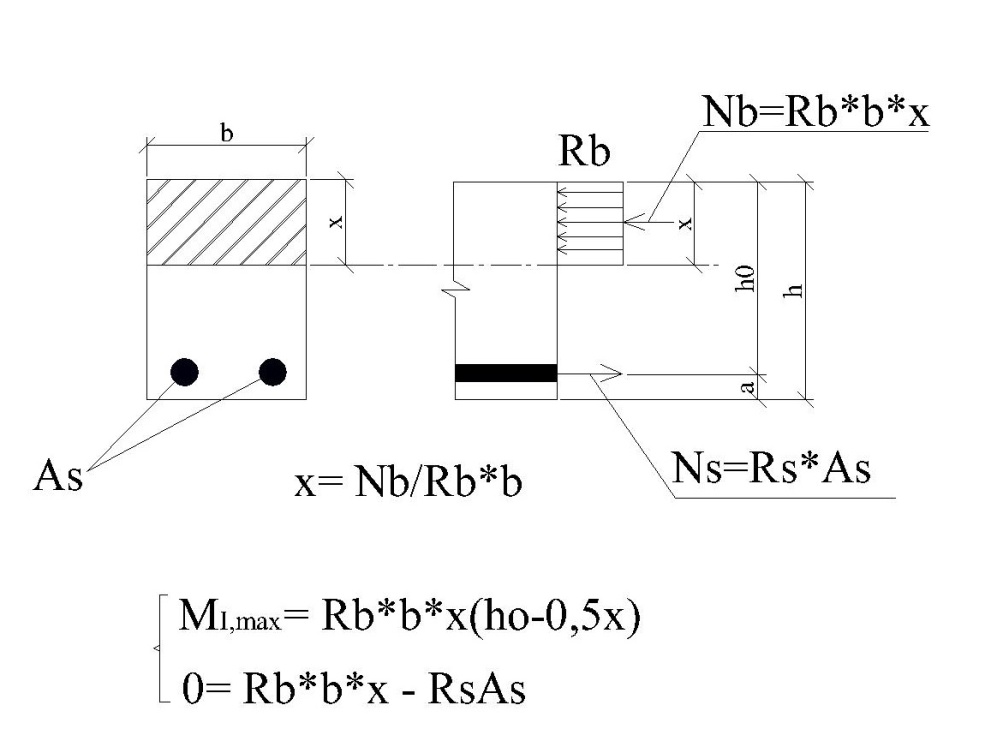
Осуществляется из условия прочности нормальных сечений изгибаемых элементов при оптимальном для балок значении относительной высоты сжатой зоны ξ=x/h₀=0,4 (сжатую продольную арматуру здесь не учитываем) и, согласно 6.2.33 [2], условия (6.65) прочности бетонной полосы между наклонными сечениями.

Определяем максимальные значения положительного изгибающего момента в 1-м пролете и поперечной силы слева от опоры В от полной расчетной нагрузки q = 188,63 кН/м.

М_l,max = *q * l²₀₁ = 0,091*188,63*5,25² = 473,12 кНм;

Q_B,лев = *q * l₀₁ = 0,6*188,63*5,25 = 594,18 кН.

Значению ξ = 0,4 соответствует α_m= 0,32 (получено из таблицы прил. 4 МУ). Руководствуясь рис 2.г МУ, определяем рабочую высоту сечения из 1-го условия по формуле:

(1)

Теперь определяем рабочую высоту сечения из условия, где коэффициент φ_b1 = 0,3 (для простоты значения поперечной силы принимаем непосредственно у опоры В):

(2)

В формулах (1) и (2) R_b выражено в кН/см², а М_{I, max} в кНсм.

Задаемся диаметром стержня d=32 мм. Тогда толщина защитного слоя бетона а_b=35 мм. Она должна составлять не менее диаметра стержня и не менее 20 мм. Кроме того, должна быть кратна 5 мм в целях стандартизации фиксаторов положения. Расстояние между осями продольных стержней, расположенных в 2 ряда по высоте сечения балки V₁ = 70 мм. (прил.6 МУ)

Величина a=a_b+0,5d+0,5V₁=35+0,5∙32+0,5∙70=8,6 см. Тогда высота сечения h=h₀+a=67,4+8,6=76см. Принимаем h=80см. Отношение ширины сечения к его высоте b/h=25/80=0,31 удовлетворяет рекомендуемое (0,3…0,5).

В связи с тем, что уточненные размеры сечения балки больше предварительно принятых (h=50 см, b=25 см), собственный вес балки увеличивается, что приводит к увеличению постоянной и полной нагрузок, расчетные значения которых на 1 метр ригеля составляют g = 17,89 кН и q =190,69 кН. Им соответствуют значения М_I,max = 478,29 кНм и Q_В,лев =600,67 кН. По этим усилиям, пользуясь формулами (1) и (2), снова определяем рабочую высоту сечения при b = 25 см и получим соответственно h_о = 67,82 cм и h_о = 61,61 см. Окончательно принимаем во всех пролетах h = 80 cм и b = 25 см.

Теперь, пользуясь тем же рисунком прил. 5, вычисляем положительные (в точках 1,2,3,4,6,7,8,9 и максимальных в 1-м и 2-м пролетах) и отрицательные (в точках 5,6,7,8,9 и 10) изгибающие моменты и максимальные поперечные силы на опорах А, В и С по формулам:

₀²

₀

α = 0,4 – на опоре А.

α = 0,6 – на опоре В слева.

α = 0,5 – на опоре В справа, на опоре С слева и справа.

Отрицательные моменты (в точках 5,6,7,8,9 и 10) вычисляются по тому же приложению, но при этом коэффициент следует принимать не по рисунку, а из таблицы. Если соотношение временной и постоянной расчётной нагрузок p/g > 5 ( p/g = 172,8/17,89 = 9,66), то коэффициент из указанной таблицы принимаются как для p/g =5

В результате вычислений получены следующие значения изгибающих моментов и поперечных сил от действия уточненной полной расчетной нагрузки на ригель.

Положительные изгибающие моменты, кНм:

М₁= 0,065∙190,69 ∙(5,25)²=341,6 кНм

М₂= 0,09∙190,69 ∙(5,25)²=473 кНм

М_I,max=0,091∙190,69 ∙(5,25)²=478,3 кНм

М₃= 0,075∙190,69 ∙(5,25)²= 394,2 кНм

М₄= 0,020∙190,69 ∙(5,25)²=105,1 кНм

М₆= М₉ = 0,018∙190,69 ∙(4,8)²=79,1 кНм

М₇= М₈ =0,058∙190,69 ∙(4,8)²=254,8 кНм

М_IImax=0,0625∙190,69∙(4,8)²= 274,6 кНм

Отрицательные изгибающие моменты, кНм:

М₅= - 0,0715∙190,69 ∙(5,25)²= -275,8 кНм

М₆= - 0,040∙190,69∙(4,8)²= - 175,7 кНм

М₇=- 0,024∙190,69 ∙(4,8)²= - 105,4 кНм

М₈= - 0,021∙190,69 ∙(4,8)²= - 92,3 кНм

М₉= - 0,034∙190,69 ∙(4,8)²= - 149,4 кНм

М₁₀= - 0,0625∙190,69 ∙(4,8)²= -274,6 кНм

Поперечные силы, кН

Q_А = 0,4∙190,69 ∙5,25= 400,4 кН

Q_В,лев = 0,6∙190,69 ∙5,25= 600,7 кН

Q_В,прав= Q_С = 0,5∙190,69 ∙4,8=457,6 кН

Соединив соответствующие ординаты в указанных точках, получим огибающую эпюру изгибающих моментов.