5 Есептік-сызбалы жұмыстарын орындау үшін әдістемелік нұсқаулар

5.1 Тәуелді қорек көзі бар электр тізбегін тұрақты токта есептеу.

Тәуелді емес қорек көзі бар тізбектерін есептеу үшін пайдаланатын барлық әдістер тәуелді қорек көзі бар тізбегін есептеу үшін де пайдаланады. Көбіне контурлық токтар әдісі (КТӘ) және түйіндік потенциалдар әдісі (ТПӘ) пайдаланылады. Барлық теңдеулер тәуелді қорек көзі бар тізбектеріндегідей құрастырылады және де теңдеулер саны өзгермейді. Құрастырылып отырған теңдеулерге байланысты, тәуелді қорек көздерінің кернеулерінің немесе токтарының теңдеулері белгісіз мәндерге байланысты көрсетіледі. Мысалға, токпен басқарылатын тәуелді қорек көзі бар кернеу теңдеуінде контур тогы I контурлық ток әдісінде токпен , ал түйіндік потенциалдар әдісінде бұл ток Ом заңына байланысты потенциалдар айырымынан анықталып алмастырылады. Мұндағы кедергілер матрицасы (КТӘ) және өтімділік матрицасы басты диагналына байланысты симметриялық емес болып табылады.

Эквивалент генератор әдісін пайдаланғанда анықталатын тогы бар тармағын ажыратып, сол ажыратылған қысқыш аралығындағы кернеуді анықтау қажет. Содан кейін соңғы тізбекке байланысты кіріс кедергісін анықтаймыз. Тәуелді қорек көзі бар тізбегінің кедергісін қалыптасқан сұлба бойынша анықтауға мүмкіндік жоқ екеніне көңіл бөлуіміз қажет. Ажыратылған қысқыштарға байланысты тізбектегі кіріс кедергісін есептеу үшін, кіріске өз қалауымызша кернеу таңдап алып, кірістегі тармақ тогын кез келген әдіспен есептеп алуымыз қажет. Ажыратылған қысқыштарға байланысты кіріс кедергісі

байланысы арқылы анықталады. Бұл жағдайда тәуелді қорек көзі сұлбада қалады.

Мысалға, тәуелді қорек көзі бар тізбек үшін, кіріс кедергісін мына теңдеу бойынша анықтауға болады:

.

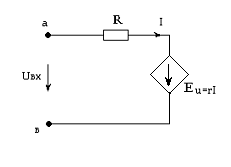
Ом заңына байланысты,

_немесе ,

сонда

Немесе, қима тогымен тармақты тұйықтап кез келген әдіспен есептеуге болады, сонда

5.2 Синусоидалы емес қорек көзі бар электр тізбегін есептеу

Периодтық гармоникалық емес f(t) функциясы, Дирихле шартын қанағат етеді, Фурье қатарына жіктеле алады.

мұндағы ω=2π/T, a_k, b_k – теңдеумен анықталатын қатардағы коэффициенттер.

- f(t) функциясының орта период мәні және тұрақты құрастырушы немесе нөлдік гармоника деп аталады.

Фурье қатарын басқа түрде де көрсетуге болады

мұндағы ,

_{Теңдеуді периодтық функция f(t) тұрақты құраушысының қосындысы және k жиіліктің гармоникалық тербелісі амплитудасымен ск және бастапқы фазасы  к ретінде түсінуге болады. Егер абциса осінде жиіліктің гармоникалық құраушысын k және сол нүктелерде перпендикулярлар құрастырсақ, ол ск ұзындығына тең болса, онда мұндай сызба амплитудалық-жиілікті спектр функциясы f(t) болып табылады. Аналогты сызбасы, бастапқы фазасында  к, f(t) фаза-жиілікті спектр фазасы көрсетілген. Периодтық функциялар f(t) дискретті спектр болып табылады.}

_{Егер тізбекте периодтық синусоидалы кмес кернеуге қосылған болса, онда тізбектегі элементтерінің тогы мен кернеуі әрқайсысына символдық әдіспен бөлек-бөлек есептеулер жасалынады. Мұндағы к-лы гармоника үшін индуктивтілікті және сыйымдылықты кедергілері}

_{тең. Тұрақты құрастырушысының есептелуі тізбектегі тұрақты ток әдісімен есептеліп, мұндағы орам тұрақты ток үшін қысқа тұйықталған бөлігіне, ал сыйымдылықты тармағы ажыратылған бөлікке айналады. Беттесу мақсатын пайдалана отырып, тармақ бойындағы лездік токтың мәнін токтың құрастырушы мәнінен анықтаймыз}

мұндағы I₀ – токтың тұрақты құрастырушысы;

I_mk- k-лы гармониканың амплитуда тогы;

Ψ_ik- k-лы гармониканың бастапқы фазасы.

Периодтық синусоидалы емес токтың I әсерлік мәні оның I_k гармоникасының әсерлік мәнімен анықталады.

Сол сияқты кернеудің әсерлік мәні мына түрде анықталады.

Периодтық симметриялы емес сигналдың активті қуаты бөлектенген гармоникасының активті қуаттың қосындысына тең.

Сол сияқты реактивті қуат анықталады.

Толық қуат токтың және кернеудің әсерлік мәндерінің туындысы ретінде анықталады.

.